摘要安全多方计算在经典密码学中一直扮演着重要的角色。量子同态加密(QHE)可以在不解密的情况下对加密数据进行计算。目前,大多数协议使用半诚实的第三方(TP)来保护参与者的秘密。我们使用量子同态加密方案代替TP来保护各方的隐私。在量子同态加密的基础上,提出了一种安全的多方量子和方案,其中N个参与者可以委托一个具有强大量子计算能力的服务器协助计算。通过将计算和密钥更新过程委托给服务器和半诚实的密钥中心,参与者使用泡利算子加密他们的私有信息数据以获得总和。此外,服务器可以自行设计和优化求和线,即使秘密信息为负,也能得到正确的结果。正确性分析表明,参与者能够正确地获得计算结果。安全性分析证明,该方案既能抵抗外部攻击,又能抵抗参与者自身的攻击,并能抵抗多达N-2个参与者的合谋攻击。从理论上讲,该协议可以推广到其他安全的多方计算问题。
QOTP
量子同态加密方案包括四种算法,每种算法的实现过程如下。
- 密钥生成算法。客户端使用安全参数的一元表示作为算法的输入,获得一组密钥,即经典公开加密密钥pk、经典秘密解密密钥sk和量子评估密钥 ρ e v k ρ_evk ρevk。
- 加密算法。客户端根据加密密钥pk的值对明文信息M进行加密,并将加密后的信息C发送给服务器。加密是由多个X和Z门组合后形成的结果。
- 同态求值算法。服务器对接收到的加密信息C执行一元算子U,并将评估信息E发送给客户端。这个过程将消耗量子评估密钥。
- 解密算法。由于服务器执行了幺正算子U,客户端更新解密密钥sk对接收到的求值信息e进行解密,客户端的解密信息本质上就是作用于明文信息M的幺正算子U。
OTP的加密公式如下所示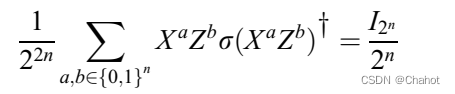
基于该加密公式的变式如下所示: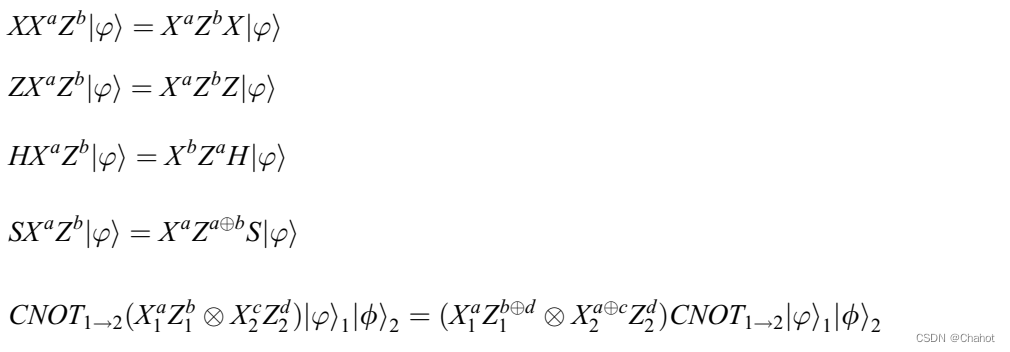
当服务器执行T或Ty门的评估时,会发生意外的s错误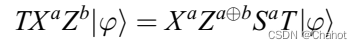
如果只对求值结果执行X和Z,则不能完全得到T|φ >,可能会出现s误差。为了消除s误差,Gong等基于u旋转贝尔测量的思想,设计了如图所示的量子电路来完成t门的同态评价过程。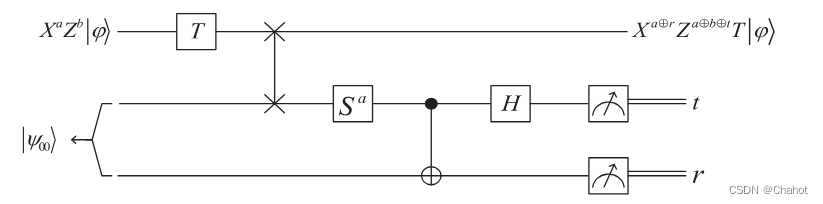
根据加密密钥a的值,客户端进行Sa旋转贝尔测量,得到r和t的值。根据密钥更新算法,客户端将解密密钥更新为
a
⊕
r
a\oplus r
a⊕r和
a
⊕
r
⊕
t
a\oplus r \oplus t
a⊕r⊕t,用于解密算法,完成t门的求值。
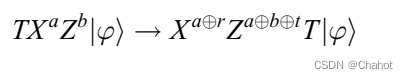
量子全加法器电路
在本节中,我们描述了如何构建一个基于经典二进制加法的量子全加法器电路。假设有两个无符号二进制数,A=(a0,a1,…,an-1)和B=(b0,b1,…,bn-1)。这两个数的和是C = (c0, c1,…,cn),其中q是进位量子位。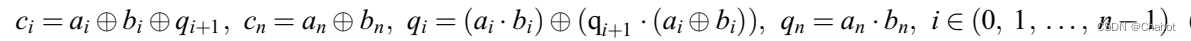
二进制加法包括异或运算和与运算。量子电路中的CNOT和Toffoli门完成这两种操作。由CNOT门和Toffoli门组成的两个参与者的全加法器电路,一个两位量子全加法器电路如下图所示。
Toffoli门可分解为2个H门、1个S门、6个CNOT门、3个t门和4个ty门,详细电路如下图所示。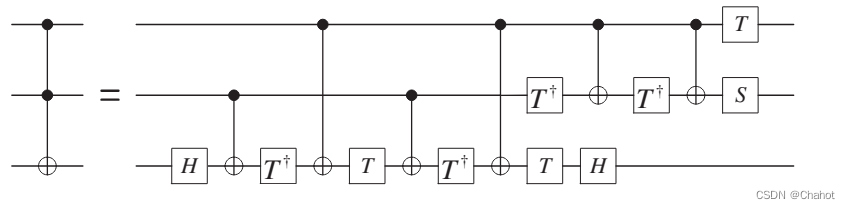
Toffoli门的详细分解电路是实现2位量子全加法器的基本元件。它将三量子位门的实现转化为单量子位和双量子位门的组合,在一定程度上易于实验和技术实现。
在我们的协议中,要加密的参与者的消息是经典的二进制数据,可以通过利用水平和垂直极化来表示。垂直偏振光子|1 >表示1,水平偏振光子|0 >表示0。在传输这些光子之前,所有的光子都是使用QOTP加密。请注意,如果加密消息是经典的,则可以使用QOTP生成完全安全的密文。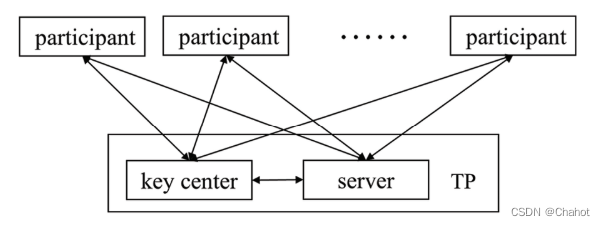
假设有N个参与者(P1, P2,…,Pn),每个参与者都持有一个只有他们自己知道的m长度的秘密信息Ii(i = 1,2,…,N)。它们可以借助服务器和可信密钥中心计算出Ii的总和,它们与TP之间的通信模型如上图所示。为了防止计算溢出,需要一个安全参数K,其中K = [log2(N)] + 2。在下图中,我们展示了该方案的流程图。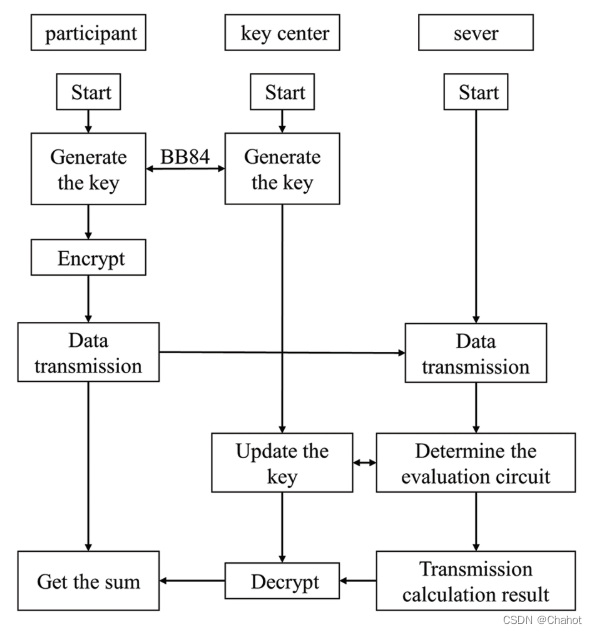
- 密钥中心随机生成N个长度为2m的密钥,并通过安全的密钥分发协议(如BB84协议)将 K e y i 0 Key^0_i Keyi0发送给参与者Pi。
- 如果参与者的秘密信息 I i I_i Ii的数量为正或零,参与者不必对他们的0-1代码做任何事情。否则,它们将0-1代码转换为2的补码。然后他们准备光子序列 ∣ ψ 1 i ⟩ . . . ∣ ψ M i ⟩ |\psi^i_1\rangle...|\psi^i_M\rangle ∣ψ1i⟩...∣ψMi⟩基于它们的0-1编码,如果 B i n j i = 1 Bin^i_j=1 Binji=1,则 ∣ ψ j i ⟩ = ∣ 1 ⟩ |\psi^i_j\rangle=|1\rangle ∣ψji⟩=∣1⟩;如果 B i n j i = 0 Bin^i_j=0 Binji=0,则 ∣ ψ j i ⟩ = ∣ 0 ⟩ |\psi^i_j\rangle=|0\rangle ∣ψji⟩=∣0⟩。然后使用 K e y i 0 Key^0_i Keyi0对光子序列进行加密,基于QOTP得到 ∣ Ψ 1 i ⟩ . . . ∣ Ψ M i ⟩ |\Psi^i_1\rangle...|\Psi^i_M\rangle ∣Ψ1i⟩...∣ΨMi⟩= X a 1 ( 0 ) Z b 1 ( 0 ) ∣ ψ 1 i ⟩ . . . X a M + L ( 0 ) Z b M + L ( 0 ) ∣ ψ M i ⟩ X^{a_1(0)}Z^{b_1(0)}|\psi^i_1\rangle...X^{a_{M+L}(0)}Z^{b_{M+L}(0)}|\psi^i_M\rangle Xa1(0)Zb1(0)∣ψ1i⟩...XaM+L(0)ZbM+L(0)∣ψMi⟩。最后,密钥中心根据安全参数k添加2K零密钥。 参与者在光子序列前加上k长度为|0>的光子,则新光子序列为 ∣ 0 1 ⟩ . . . ∣ 0 k ⟩ ∣ Ψ 1 i ⟩ . . . ∣ Ψ M i ⟩ |0_1\rangle...|0_k\rangle|\Psi^i_1\rangle...|\Psi^i_M\rangle ∣01⟩...∣0k⟩∣Ψ1i⟩...∣ΨMi⟩.信息为负的参与者在光子序列前添加k长度|1 >个光子,新光子序列为 ∣ 1 1 ⟩ . . . ∣ 1 k ⟩ ∣ Ψ 1 i ⟩ . . . ∣ Ψ M i ⟩ |1_1\rangle...|1_k\rangle|\Psi^i_1\rangle...|\Psi^i_M\rangle ∣11⟩...∣1k⟩∣Ψ1i⟩...∣ΨMi⟩。
- 为了防止被窃听,参与者准备了Di个诱饵光子,并随机插入到自己的光子序列中,每个光子从{|0 >,|1 >,|+ >,|−>}中选择,并将新的光子序列发送给服务器。
- 一旦服务器获得他们的光子序列,参与者宣布插入的诱饵光子的位置 P o i Po^i Poi和 b a s e B a i base Ba^i baseBai。如果插入诱饵为|0 >或|1 >,则测量基为{|0 >,|1 >};若插入诱饵为|+>或|−>,则测量基为|+>或|−>。服务器根据测量结果计算准确度,如果准确度低于预设的阈值,则表示存在窃听者,然后终止协议。否则,服务器将丢弃这些诱饵光子并继续下一步。
- 服务器构建一个量子全加法器电路,每个参与者的光子序列作为电路的输入。在评估操作中,密钥中心根据服务器执行的量子门和量子门的密钥更新算法更新密钥。在服务器执行完量子电路中的所有量子门后,密钥中心获得最终更新的 K e y i f i n a l Key^{final}_i Keyifinal,即解密密钥。服务器将计算结果发送到密钥中心。
- 密钥中心使用解密密钥对光子序列中的所有光子进行解密和测量,然后将测量结果释放给所有参与者。然后参与者计算比特序列,得到他们的秘密信息的总和。
在步骤5中,在同态求值算法中,当服务器对密文进行Clifford gate运算时,根据Clifford gate与泡利矩阵之间的交换规则,无需额外的经典资源或量子资源即可获得新的中间密钥。假设服务器执行的第i次Clifford gate操作定义为Gi,作用于光子序列
G
i
X
a
k
(
j
)
Z
b
k
(
j
)
∣
ψ
⟩
G_iX^{a_k(j)}Z^{b_k(j)}|\psi\rangle
GiXak(j)Zbk(j)∣ψ⟩中的第k个,(如果Gi = CNOT,输入量子位分别为k和l,则
G
i
X
a
k
(
j
)
Z
b
k
(
j
)
∣
ψ
⟩
⊗
G
i
X
a
l
(
j
)
Z
b
l
(
j
)
∣
ψ
⟩
G_iX^{a_k(j)}Z^{b_k(j)}|\psi\rangle\otimes G_iX^{a_l(j)}Z^{b_l(j)}|\psi\rangle
GiXak(j)Zbk(j)∣ψ⟩⊗GiXal(j)Zbl(j)∣ψ⟩,其中Gi∈{X, Y, Z, H, T, S, CNOT}, ak(j), bk(j)为(j+1)-中间密钥。对于操作Gi和密钥更新算法,第j+1中间密钥的计算过程如下:
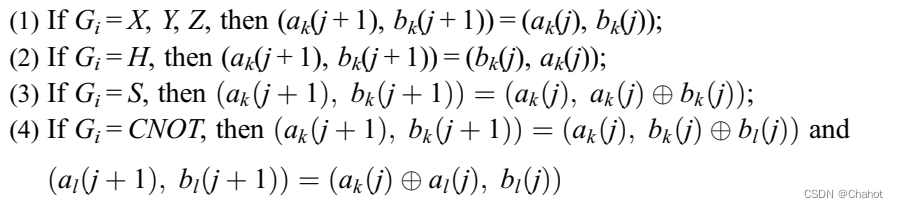
任何任意的酉算子都可以由H、S、CNOT和T门组成,并且客户端需要T门键更新才能在服务器上执行任何酉操作。但是当t门作用于加密的量子位时,就会发生s错误。
版权归原作者 Chahot 所有, 如有侵权,请联系我们删除。