密码学消息鉴别

信息安全

完整性
1.数据完整性：数据未被篡改或损坏。数据是不可否认的，发送方和接收方不能抵赖处理了数据。
2.系统完整性：系统未被非授权使用。
真实性
确认实体是它声明的，适用于用户、进程等等的合法的信息（是否真的需要）。

对于数据来说，是不存在认证和合法性校验的，所以数据的完整性只包括是否被篡改和损坏，是否被处理过。而需要将认证和合法性单独抽离出来作为一个抽象的方面。

通信系统典型攻击

数据机密性方面：窃听，业务流分析
消息鉴别方面：消息篡改（内容，顺序，时间），冒充
数字签名方面：接受者或发送者否认收到或者发送过消息。

消息鉴别

证实收到的消息来自可信的源并且未被篡改的过程。

目的：
1.验证发送者是真正的，不是冒充的，源识别。
2.验证信息的完整性，在传送过程中未被篡改。

鉴别系统

鉴别系统模型：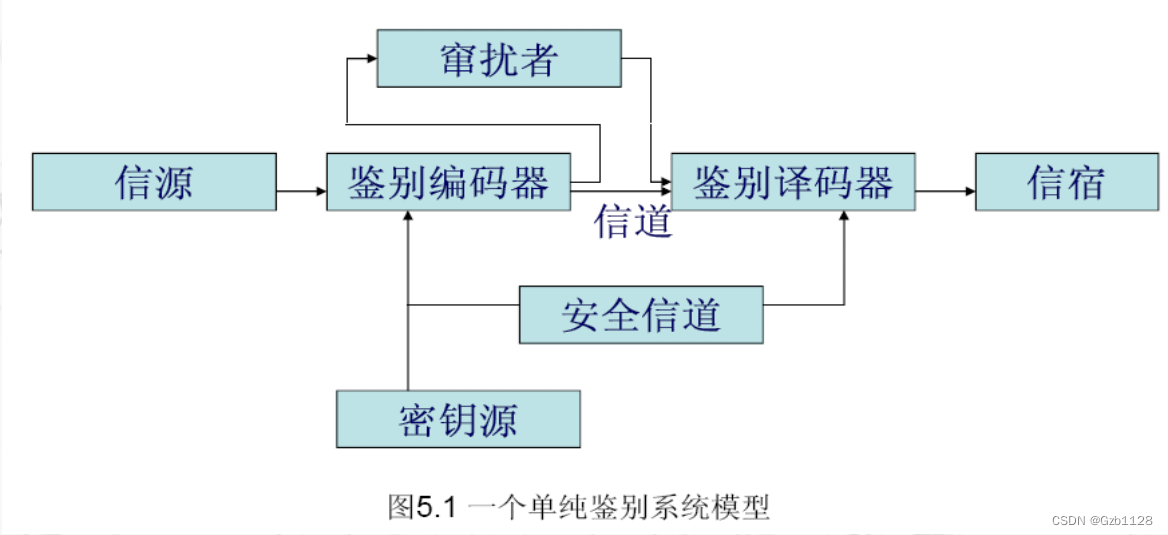

即发送方使用编码器，接收方使用译码器，攻击者可以截获信道中的鉴别文本。密钥通过安全信道发送给双方。

安全的鉴别系统需要满足：
1.接收方可以验证消息的完整性，合法性和真实性。（数据完整性以及真实性）
2.消息不能被抵赖。（数据完整性）
3.除了合法的发送者，其他人不能发送消息。（系统完整性）

鉴别编码器和译码器可以抽象成鉴别函数。函数要产生一个鉴别标识，和鉴别协议，让接受者可以完整消息鉴别。

鉴别函数分类

产生鉴别符的函数基本分成三类：
1.消息加密函数：用完整消息密文作为对信息的鉴别
2.散列函数：以一个变长的报文作为输入，输出固定长度的散列码（也叫报文摘要），是公开的函数。
3.消息鉴别码MAC：公开函数+密钥产生一个固定长度的值作为鉴别标识。

消息加密函数

对称密码的加密提供保密和鉴别（只有双方持有这对密钥）
非对称密码的加密分3种情况：
A用B公钥加密，B用B私钥解密：提供保密性，无法提供鉴别
A用A私钥加密，B用A公钥解密：由于任何人都可以用A的公钥解密，因此不提供保密性。提供鉴别和签名。
A用A的私钥加密，再用B的公钥加密，B先用B的私钥解密，再用A的公钥解密：B的公钥提供保密性、A的私钥提供鉴别和签名。

密码学散列函数

输入任意长度报文，产出固定长度的消息摘要。同时提供了错误检测的能力。也称为数字指纹。

散列函数常见用法：

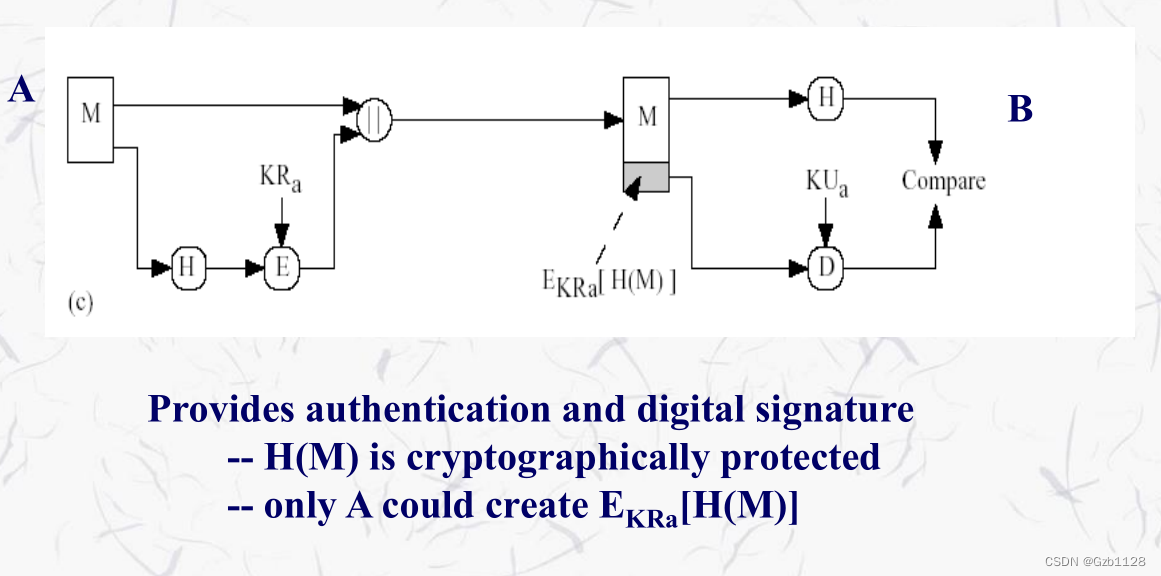
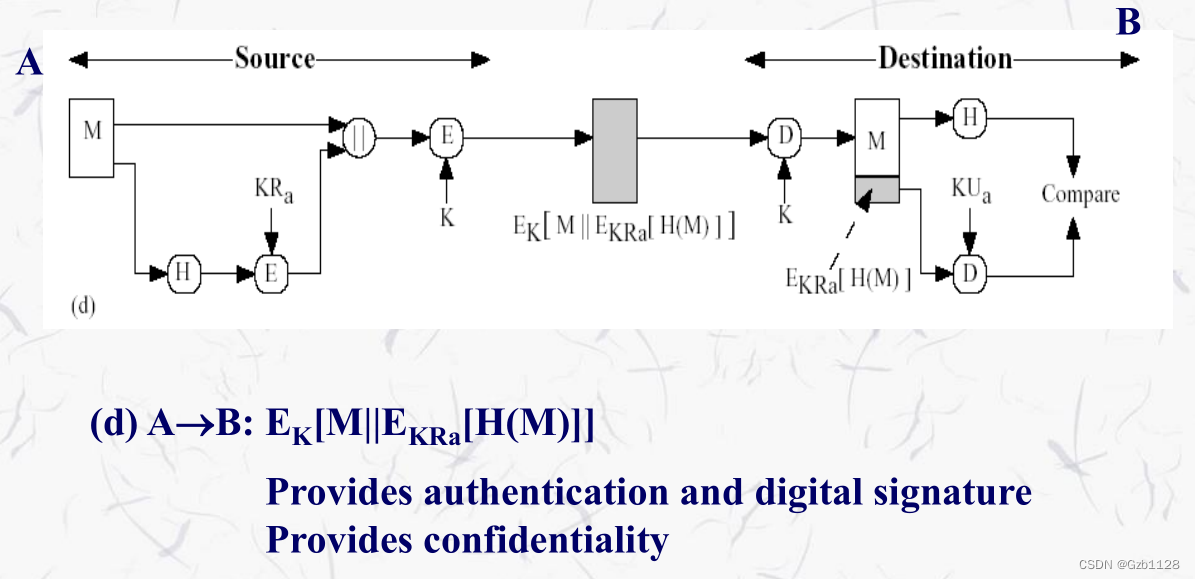
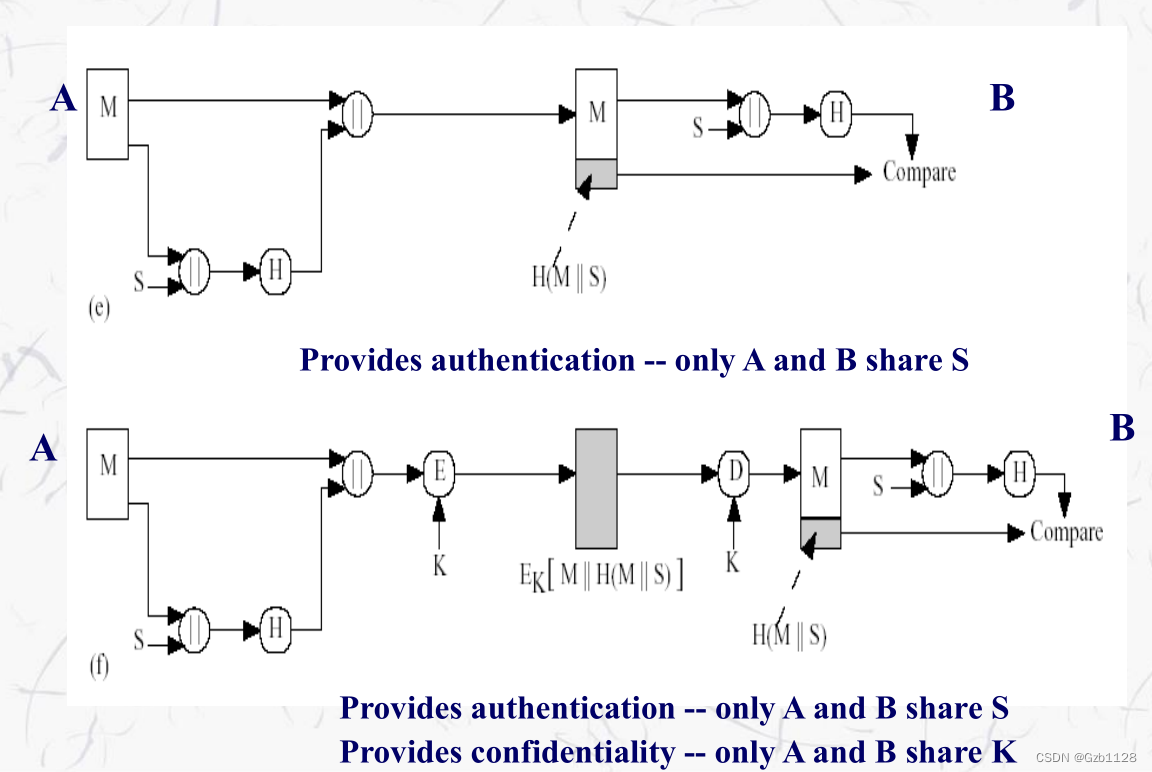
总的来说，明文被加密了就提供了保密性，散列函数提供了消息鉴别，如果利用私钥加密来提供数字签名。需要注意，消息鉴别只是提供数据完整性的保证，更多的保证要看具体的算法。而数字签名真的只是一个签名的功能，说明是公钥对应的私钥用户提供了签名。为什么对称密码没有签名功能，首先这个签名就至少有2个人可以签，因此签名一定是一个非对称下的概念。

RSA数字签名算法

公钥KU{e,n}，私钥KR{d,p,q}
将消息划分成块，使得每块P<n
签名P时，计算

    y
   
   
    =
   
   
    s
   
   
    i
   
   
    g
   
   
    (
   
   
    P
   
   
    )
   
   
    =
   
   
    
     p
    
    
     d
    
   
   
    (
   
   
    m
   
   
    o
   
   
    d
   
   
    n
   
   
    )
   
  
  
   y=sig(P)=p^d(modn)
  
 
y=sig(P)=pd(modn)

验证签名时，计算

     P
    
    
     ′
    
   
   
    =
   
   
    
     y
    
    
     e
    
   
   
    (
   
   
    m
   
   
    o
   
   
    d
   
   
    n
   
   
    )
   
   
    =
   
   
    P
   
  
  
   P'=y^e(modn)=P
  
 
P′=ye(modn)=P

就和RSA加密算法差不多

弱点：
1.任何人可以对A的签名解密，已知明文攻击是容易的
2.如果有一组

    (
   
   
    
     x
    
    
     1
    
   
   
    ,
   
   
    
     y
    
    
     1
    
   
   
    )
   
   
    ,
   
   
    (
   
   
    
     x
    
    
     2
    
   
   
    ,
   
   
    
     y
    
    
     2
    
   
   
    )
   
   
    ，
   
   
    伪
   
   
    造
   
   
    (
   
   
    
     x
    
    
     1
    
   
   
    
     x
    
    
     2
    
   
   
    ,
   
   
    y
   
   
    )
   
  
  
   (x_1,y_1),(x_2,y_2)，伪造(x_1x_2,y)
  
 
(x1​,y1​),(x2​,y2​)，伪造(x1​x2​,y)是容易的，

 
  
   
    y
   
   
    =
   
   
    
     y
    
    
     1
    
   
   
    
     y
    
    
     2
    
   
  
  
   y=y_1y_2
  
 
y=y1​y2​

解决办法：
引入散列函数并签名摘要。
验证时先用公钥解密散列函数起到签名验证，再计算明文的散列函数以鉴别。
用hash签名可以提高签名速度，不用泄露签名的信息（解密签名只能看见散列函数，不暴露明文），签名变换和加密变换分开，提供不同层次的抽象。

散列函数特性

需要保证散列函数不降低鉴别方案的安全性（因为散列函数相当于将信息降到了256维）。

如果攻击者有一个签名(x,y)，其中y是x的散列值并签名后的值。如果攻击者找得到x’使得h(x)=h(x’)，则(x’,y)也是一个合法的签名。
弱无碰撞：散列函数h是弱无碰撞的，是指给定消息x，计算上几乎找不到

     x
    
    
     ′
    
   
   
    ≠
   
   
    x
   
   
    且
   
   
    h
   
   
    (
   
   
    x
   
   
    )
   
   
    =
   
   
    h
   
   
    (
   
   
    
     x
    
    
     ′
    
   
   
    )
   
  
  
   x'\neq x且h(x)=h(x')
  
 
x′​=x且h(x)=h(x′)，也称**抗第二原像攻击（抗弱碰撞攻击）**。

如果攻击者找到了一对明文x,x’,使得h(x)=h(x’)，则攻击者让A对x签名，这个签名同样对x’合法。
强无碰撞：称散列函数是强无碰撞的，是指无法在计算上找到一对x和x’使得h(x)=h(x’),也称抗强碰撞攻击。
强无碰撞是为了对抗生日攻击方法的防御方法。生日攻击表明对于n的取值空间，大约取

     n
    
   
  
  
   \sqrt n
  
 
n​个的随机变量就可以有一对随机变量碰撞在一起。

单向的：称散列函数是是单向的，是指计算h的逆

     h
    
    
     
      −
     
     
      1
     
    
   
  
  
   h^{-1}
  
 
h−1在计算上不可行，也称**抗原像攻击**

hash函数通用结构

即迭代计算hash值

散列算法

MD5,SHA-1,RIPEMD-160,SHA-2,SHA-3,SM3

MD5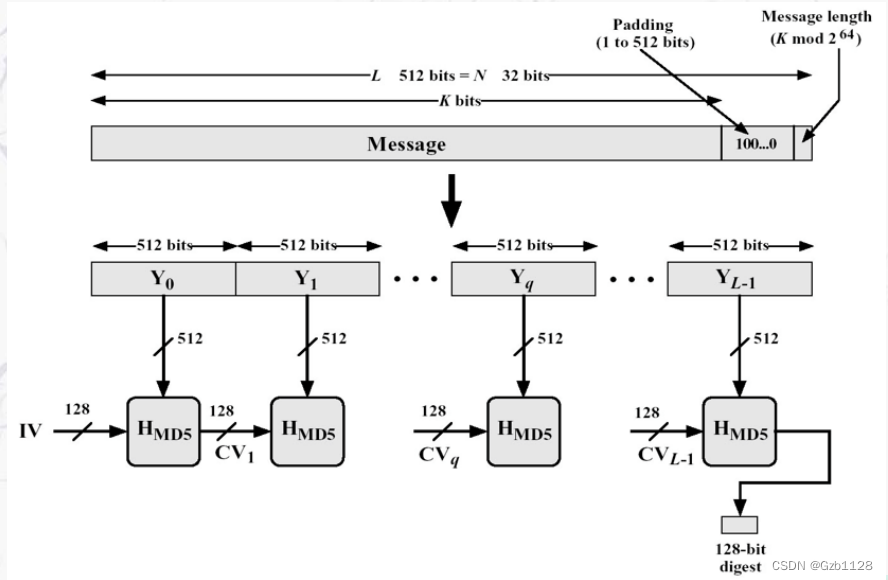

即明文分块迭代处理，密文反馈机制

消息鉴别码MAC

利用明文和密钥生成一个固定大小的数据块，称为MAC或者消息校验和。有点类似带密钥的hash算法。

作用：
1.接受者确保信息未被改变
2.确信信息来自发送者
3.如果消息中包含顺序码，接受者可以保证消息的正常顺序。
因此MAC和散列函数类似提供了一个鉴别的功能。

分组密码CMAC算法

CBC-MAC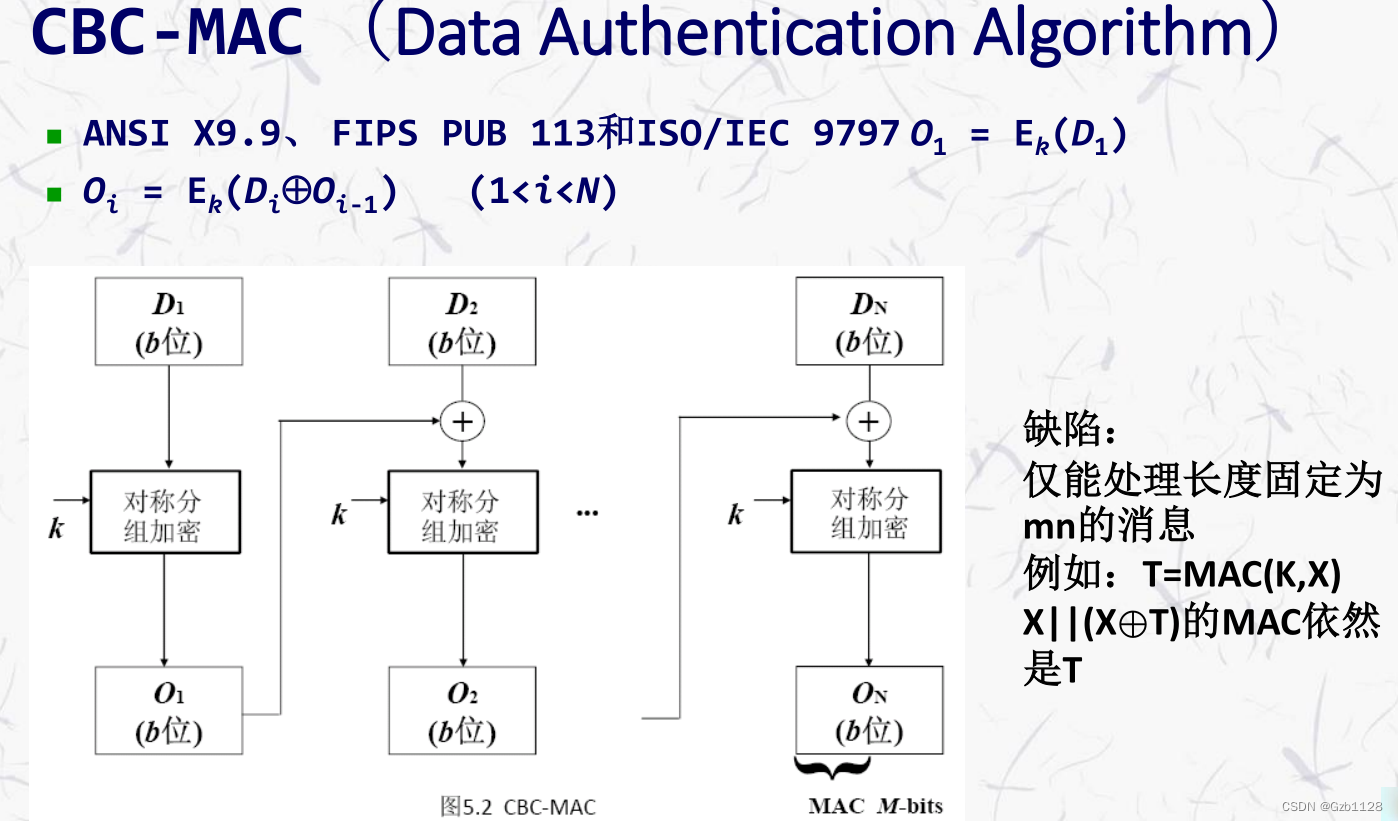

可以看到和分组对称密码中的CBC算法类似，因为MAC也是一个对称密码

类似的CFB-MAC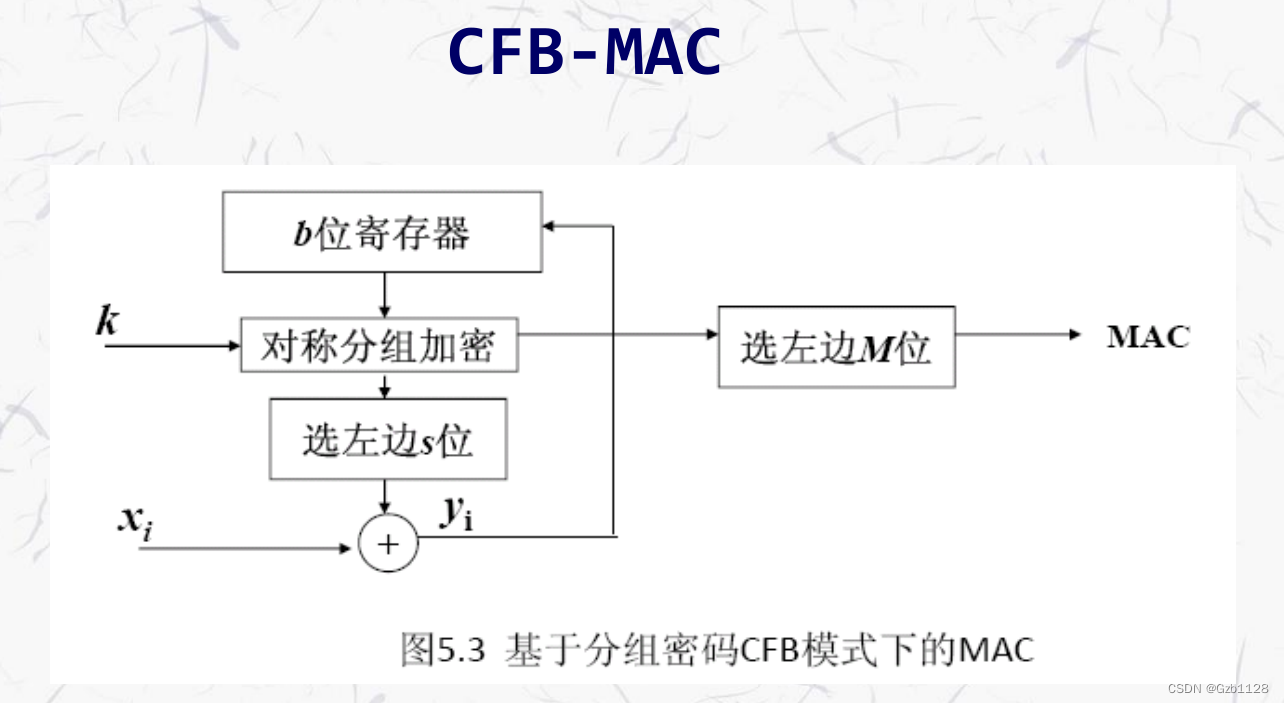

基于hash的HMAC算法

HMAC和hash算法是解耦的，这样可以使用任意的hash算法。

算法：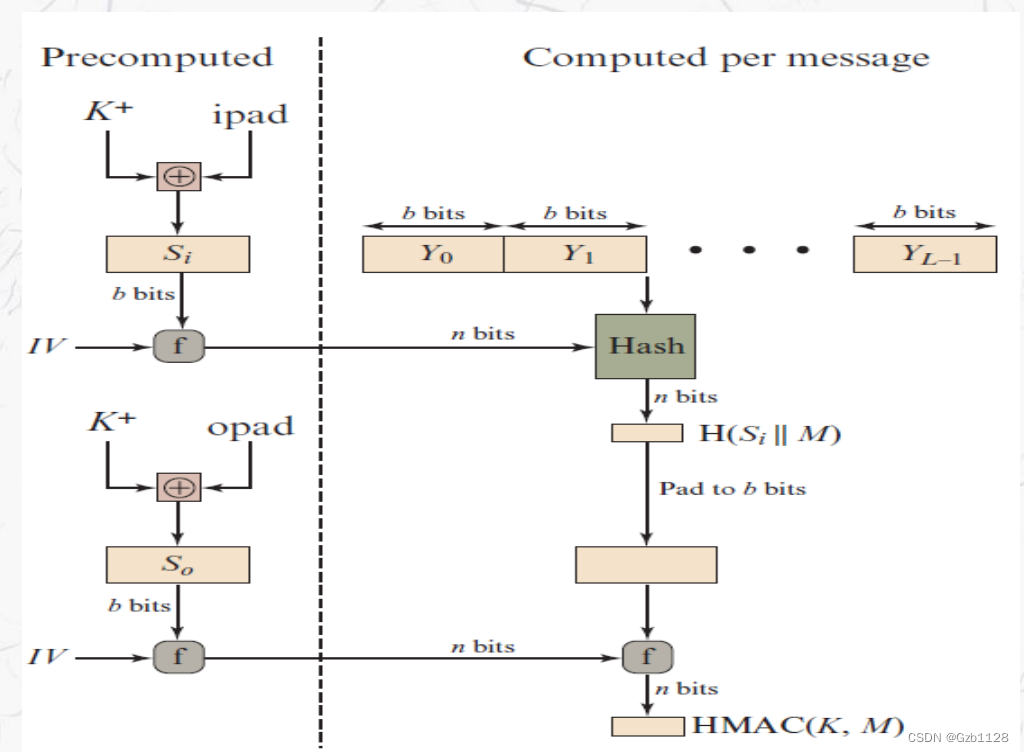

即HMAC生成消息H(K xor opad, H(K xor ipad, text)），即提供一个密钥K进去，异或来对齐密钥长度，先对明文做一次hash，再对密文做一次hash。