相似性度量在机器学习中起着至关重要的作用。这些度量以数学方式量化对象、数据点或向量之间的相似性。理解向量空间中的相似性概念并采用适当的度量是解决广泛的现实世界问题的基础。本文将介绍几种常用的用来计算两个向量在嵌入空间中的接近程度的相似性度量。
余弦相似度
余弦相似度(cos (θ))值范围从-1(不相似)到+1(非常相似)。从下图可以看出,点A(1.5, 1.5)和点B(2.0, 1.0)在二维嵌入空间中距离很近。当计算余弦相似度时,得到0.948的值也可以确认两个向量非常相似。当较点A(1.5, 1.5)和点C(-1.0, -0.5)的相似度时,余弦相似度为-0.948,表明两个向量不相似。通过观察也可以看到它们在嵌入空间中方向相反。cos (θ)值为0表示两个向量彼此垂直,既不相似也不不同。
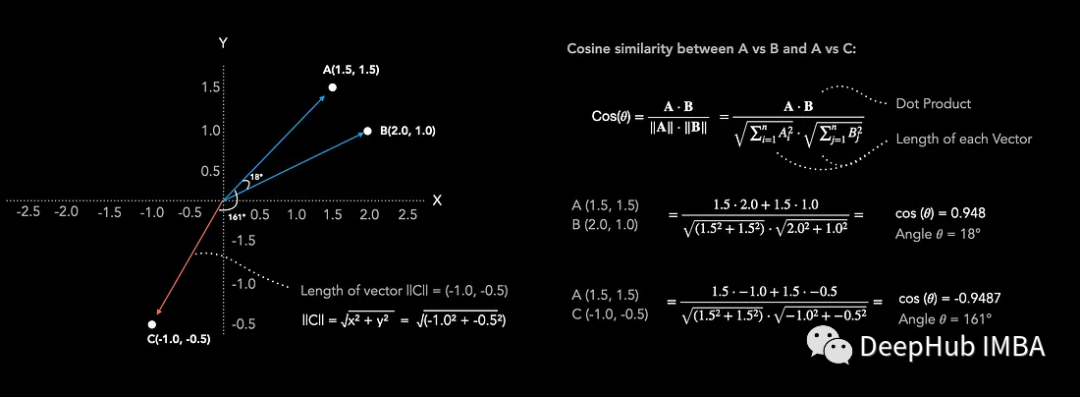
要计算两个向量之间的余弦相似度,可以简单地用两个向量的点积除以它们长度的乘积。余弦相似度主要考虑两个向量之间的角度来确定它们的相似度,并且忽略向量的长度。
在Python中计算余弦相似度很简单。我们可以将相似值cos(θ)转换为两个向量之间的角度(θ),通过取反余弦。
import torch
import torch.nn.functional as F
import math
#Create 3 Vectors
A = torch.tensor([1.5,1.5])
B = torch.tensor([2.0,1.0])
C = torch.tensor([-1.0,-0.5])
# Calculate cosine similarity cos(𝜃):
cos = F.cosine_similarity(A, B, dim=0)
print("Cosine Similarity:", cos)
# Calculate the angle 𝜃:
# acos is the inverse of cos(x)
theta = math.acos(cos)
# Convert radians to degrees
theta_degrees = math.degrees(theta)
print("Angle in radians:", theta)
print("Angle in degrees:", theta_degrees)
点积
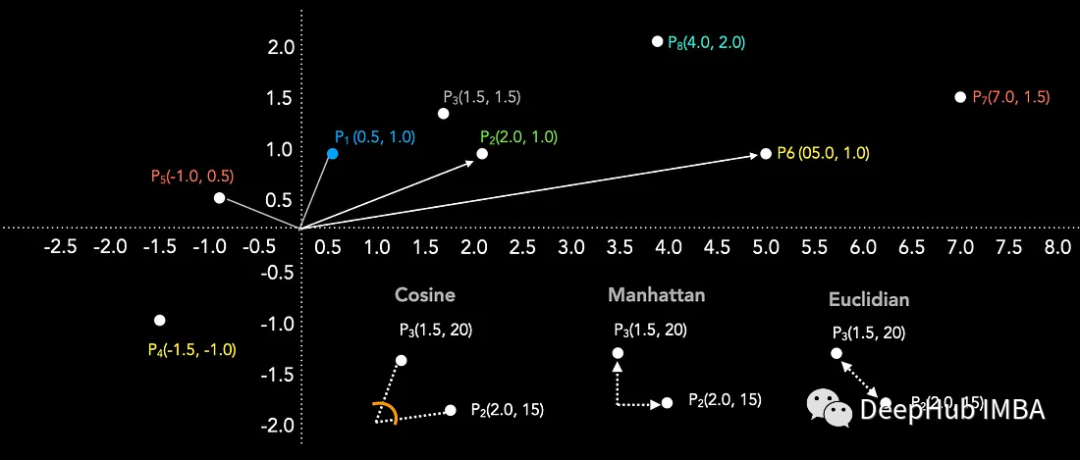
点积是一种常用的相似度度量。点积和余弦相似度是密切相关的概念。点积的取值范围从负无穷到正无穷,负值表示方向相反,正值表示方向相同,当向量垂直时为0。点积值越大表示相似性越大。下图显示了点P1与剩余点P2到P5之间的点积的计算。

点积可以从余弦方程推导出来:通过将两个向量之间夹角的余弦值乘以两个向量的长度就得到点积,如下图所示。点积受到向量嵌入长度的影响,这在选择相似性度量时可能是一个关键的考虑因素

点积是如何影响相似性度量呢?
假设你正在计算一组科学研究论文的相似度。研究论文嵌入向量的长度与被引用次数成正比。使用余弦相似度来计算研究论文之间的相似度是很常见的。如果使用点积,研究论文之间的相似性是如何变化的?
余弦相似度考虑向量的方向和大小,使其适用于向量的长度与其相似度不直接相关的情况。当使用点积时只有向量的大小起作用,方向就不那么重要了。
高被引次数(较长的向量)的论文与其他高被引论文的点积相似度得分更高,因为它们的量级对结果的贡献更大。低被引次数(较短的向量)的论文与高被引次数的论文的点积相似度得分较低,因为它们的量级较小。
曼哈顿(L1)和欧几里得(L2)距离
曼哈顿距离通过将每个维度的绝对差相加来计算距离,而欧几里得距离则计算点之间的直线距离。
曼哈顿距离适用于涉及网格状运动的场景,或者当单个维度具有不同的重要性时。当测量最短路径或当所有维度对距离的贡献相等时,欧几里得距离是理想的。
在大多数情况下,对于同一对点,曼哈顿距离比欧几里得距离产生更大的值。随着数据维数的增加,与欧几里得距离度量相比,曼哈顿距离成为首选。
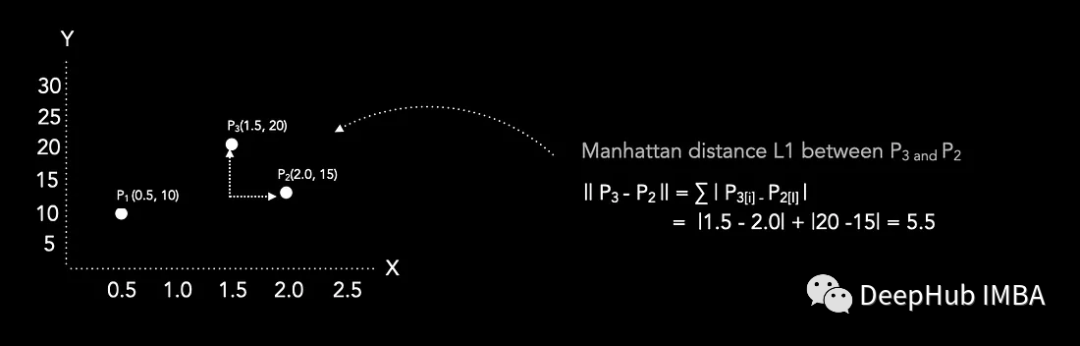
曼哈顿距离L1
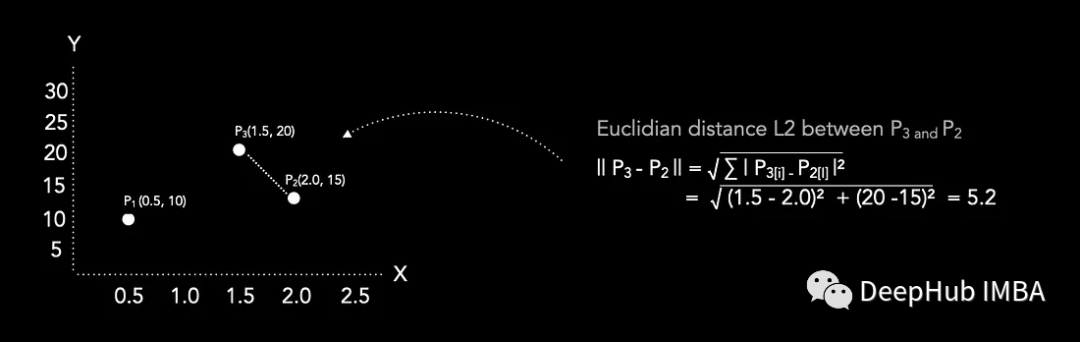
欧氏距离L2
曼哈顿距离是沿着网格线行走的距离,而欧几里得距离是直线距离。这两种距离在许多领域都有广泛的应用,例如在机器学习、图像处理、路径规划等方面。
总结
这四种距离度量方法各自有不同的应用场景和用途,选择哪种度量方法取决于具体的问题和数据类型。曼哈顿距离和欧几里得距离适用于空间坐标的距离测量。
曼哈顿距离常用于计算城市街道的距离,也用于特征选择和聚类等数据分析任务。欧几里得距离广泛用于空间中的距离测量,机器学习、数据挖掘和图形处理等领域。
点积距离和余弦相似度通常用于向量或文本数据的相似性度量。主要用于向量相似性的度量,如文本挖掘和自然语言处理中的文档相似性,或信息检索、推荐系统等领域。
作者:Frederik vl