文章目录
前言
在上篇博客中使用了
matplotlib
绘制了3D小红花，本篇博客主要介绍一下3D小红花的绘制原理。
1. 极坐标系
对于极坐标系中的一点
P
P
P，我们可以用极径
r
r
r 和极角
θ
\theta
θ 来表示，记为点
P
(
r
,
θ
)
P(r, \theta)
P(r,θ)，其相关知识在高中就已经介绍，这里不再赘述。
使用
matplotlib
绘制极坐标系：
import matplotlib.pyplot as plt
import numpy as np
if __name__ =='__main__':# 极径
r = np.arange(10)# 角度
theta =0.5* np.pi * r
fig = plt.figure()
plt.polar(theta, r, c='r', marker='o', ms=3, ls='-', lw=1)# plt.savefig('img/polar1.png')
plt.show()
使用
matplotlib
绘制极坐标散点图：
import matplotlib.pyplot as plt
import numpy as np
if __name__ =='__main__':
r = np.linspace(0,10, num=10)
theta =2* np.pi * r
area =3* r **2
ax = plt.subplot(111, projection='polar')
ax.scatter(theta, r, c=theta, s=area, cmap='hsv', alpha=0.75)# plt.savefig('img/polar2.png')
plt.show()
有关
matplotlib极坐标的参数更多介绍，可参阅官网手册。
2. 极坐标系花瓣
绘制
r
=
s
i
n
(
θ
)
r=sin(\theta)
r=sin(θ) 在极坐标系下的图像：
import matplotlib.pyplot as plt
import numpy as np
if __name__ =='__main__':
fig = plt.figure()
ax = plt.subplot(111, projection='polar')
ax.set_rgrids(radii=np.linspace(-1,1, num=5), labels='')
theta = np.linspace(0,2* np.pi, num=200)
r = np.sin(theta)
ax.plot(theta, r)# plt.savefig('img/polar3.png')
plt.show()
以
2
π
2\pi
2π 为一个周期，增加图像的旋转周期：
r = np.sin(2* theta)
继续增加图像的旋转周期：
r = np.sin(3* theta)
r = np.sin(4* theta)
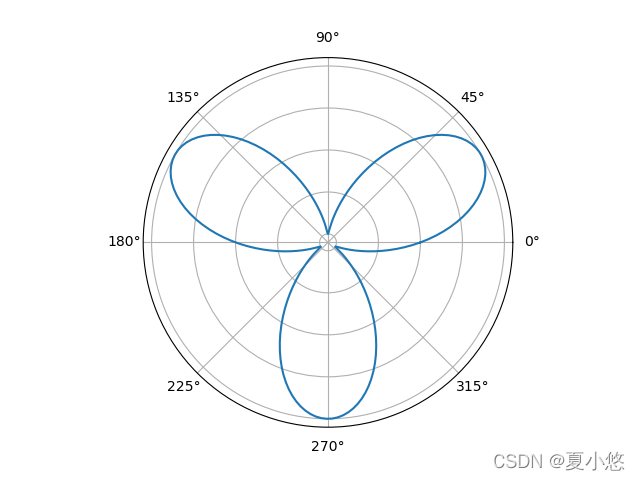
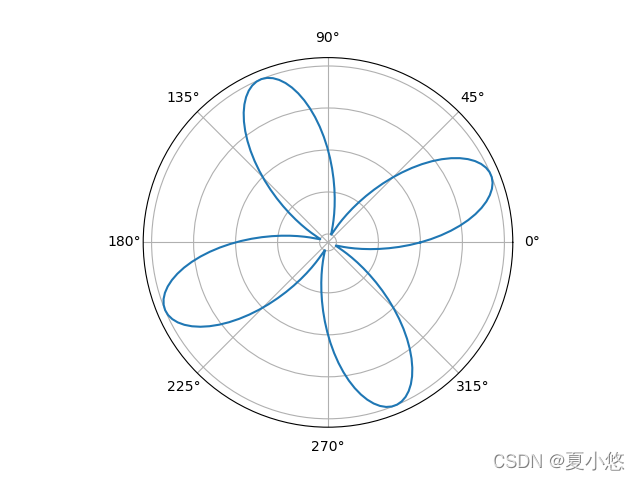
然后我们可以通过调整极径系数和角度系数来调整图像：
import matplotlib.pyplot as plt
import numpy as np
if __name__ =='__main__':
fig = plt.figure()
ax = plt.subplot(111, projection='polar')
ax.set_rgrids(radii=np.linspace(-1,1, num=5), labels='')
theta = np.linspace(0,2* np.pi, num=200)
r1 = np.sin(4*(theta + np.pi /8))
r2 =0.5* np.sin(5* theta)
r3 =2* np.sin(6*(theta + np.pi /12))
ax.plot(theta, r1)
ax.plot(theta, r2)
ax.plot(theta, r3)# plt.savefig('img/polar4.png')
plt.show()
3. 三维花瓣
现在可以将花瓣放置在三维空间上了，根据花瓣的生成规律，其花瓣外边缘线在一条旋转内缩的曲线上，这条曲线的极径
r
r
r 随着角度的增大逐渐变小，其高度
h
h
h 逐渐变大。
因此我们在
f
(
x
)
=
e
−
x
f(x) = e^{-x}
f(x)=e−x 的基础之上定义了一个递减函数，保证其值域在
(
0
,
π
2
]
(0, \frac {\pi} {2}]
(0,2π]，新的函数为：
f
(
θ
)
=
π
2
e
−
θ
f(\theta)=\frac {\pi} {2} e^{-\theta}
f(θ)=2πe−θ 其函数图像如下：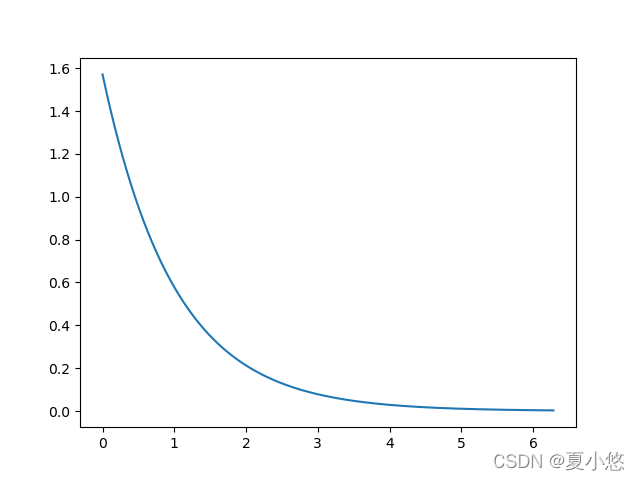
这样定义
r
=
s
i
n
(
f
)
,
h
=
c
o
s
(
f
)
r=sin(f), h=cos(f)
r=sin(f),h=cos(f) 就满足前面对花瓣外边缘曲线的假设了，即
r
r
r 递减，
h
h
h 递增。
现在将其放在三维空间中：
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
if __name__ =='__main__':
fig = plt.figure()
ax = Axes3D(fig)# plt.axis('off')
x = np.linspace(0,1, num=30)
theta = np.linspace(0,2* np.pi, num=1200)
theta =30* theta
x, theta = np.meshgrid(x, theta)# f is a decreasing function of theta
f =0.5* np.pi * np.exp(-theta /50)
r = x * np.sin(f)
h = x * np.cos(f)# 极坐标转笛卡尔坐标
X = r * np.cos(theta)
Y = r * np.sin(theta)
ax = ax.plot_surface(X, Y, h,
rstride=1, cstride=1, cmap=plt.cm.cool)# plt.savefig('img/polar5.png')
plt.show()
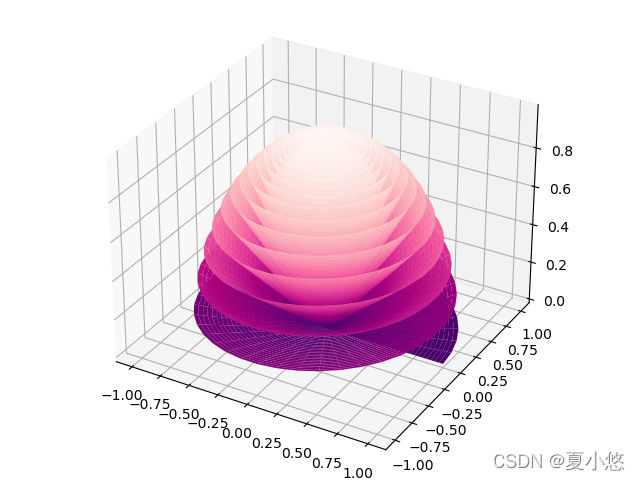
笛卡尔坐标系
(Cartesian coordinate system)，即直角坐标系。
然而，上述的表达仍然没有得到花瓣的细节，因此我们需要在此基础之上进行处理，以得到花瓣形状。因此设计了一个花瓣函数：
f
(
θ
)
=
1
−
1
−
∣
s
i
n
(
θ
2
)
∣
2
f(\theta) = 1 - \frac {1 - |sin(\frac {\theta} {2})|} {2}
f(θ)=1−21−∣sin(2θ)∣ 其是一个以
2
π
2\pi
2π 为周期的周期函数，其值域为
[
0.5
,
1.0
]
[0.5, 1.0]
[0.5,1.0]，图像如下图所示：
再次绘制：
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
if __name__ =='__main__':
fig = plt.figure()
ax = Axes3D(fig)# plt.axis('off')
x = np.linspace(0,1, num=30)
theta = np.linspace(0,2* np.pi, num=1200)
theta =30* theta
x, theta = np.meshgrid(x, theta)# f is a decreasing function of theta
f =0.5* np.pi * np.exp(-theta /50)# 通过改变函数周期来改变花瓣的形状# 改变值域也可以改变花瓣形状# u is a periodic function
u =1-(1- np.absolute(np.sin(3.3* theta /2)))/2
r = x * u * np.sin(f)
h = x * u * np.cos(f)# 极坐标转笛卡尔坐标
X = r * np.cos(theta)
Y = r * np.sin(theta)
ax = ax.plot_surface(X, Y, h,
rstride=1, cstride=1, cmap=plt.cm.RdPu_r)# plt.savefig('img/polar6.png')
plt.show()
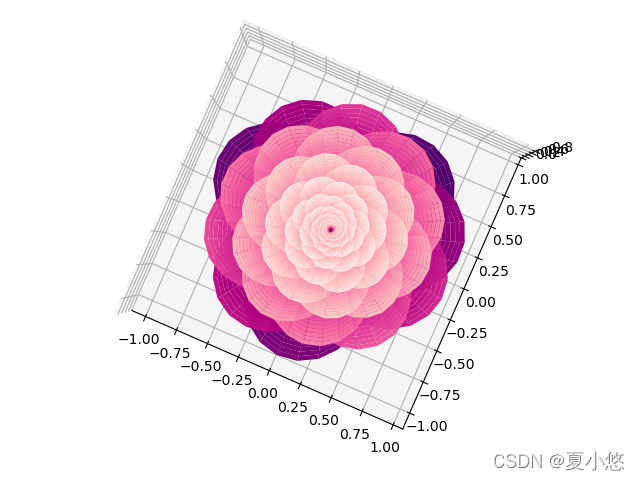
4. 花瓣微调
为了使花瓣更加真实，使花瓣的形态向下凹，因此需要对花瓣的形状进行微调，这里添加一个修正项和一个噪声扰动，修正函数图像为：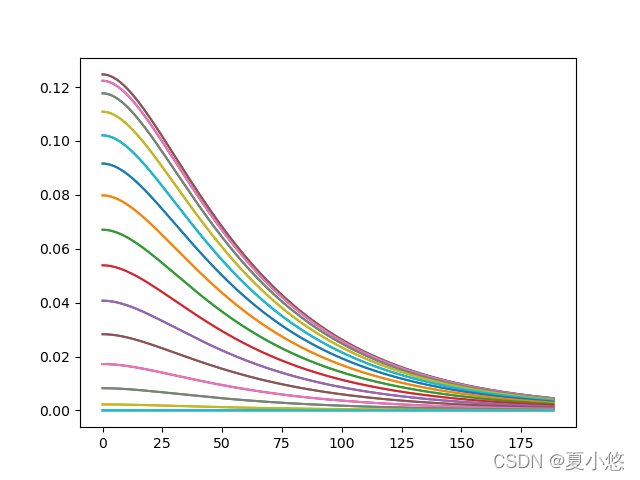
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
if __name__ =='__main__':
fig = plt.figure()
ax = Axes3D(fig)# plt.axis('off')
x = np.linspace(0,1, num=30)
theta = np.linspace(0,2* np.pi, num=1200)
theta =30* theta
x, theta = np.meshgrid(x, theta)# f is a decreasing function of theta
f =0.5* np.pi * np.exp(-theta /50)
noise = np.sin(theta)/30# u is a periodic function
u =1-(1- np.absolute(np.sin(3.3* theta /2)))/2+ noise
# y is a correction function
y =2*(x **2- x)**2* np.sin(f)
r = u *(x * np.sin(f)+ y * np.cos(f))
h = u *(x * np.cos(f)- y * np.sin(f))
X = r * np.cos(theta)
Y = r * np.sin(theta)
ax = ax.plot_surface(X, Y, h,
rstride=1, cstride=1, cmap=plt.cm.RdPu_r)# plt.savefig('img/polar7.png')
plt.show()
修正前后图像区别对比如下：
5. 结束语
3D
花的绘制主要原理是极坐标，通过正弦/余弦函数进行旋转变形构造，参数略微变化就会出现不同的花朵，有趣！
本文转载自: https://blog.csdn.net/qq_42730750/article/details/122940228
版权归原作者 夏小悠 所有， 如有侵权，请联系我们删除。
版权归原作者 夏小悠 所有， 如有侵权，请联系我们删除。