聚类-KMeans算法（图解算法原理）

文章目录

简介

k均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，也就是将数据分成K个簇的算法，其中K是用户指定的。

比如将下图中数据分为3簇，不同颜色为1簇。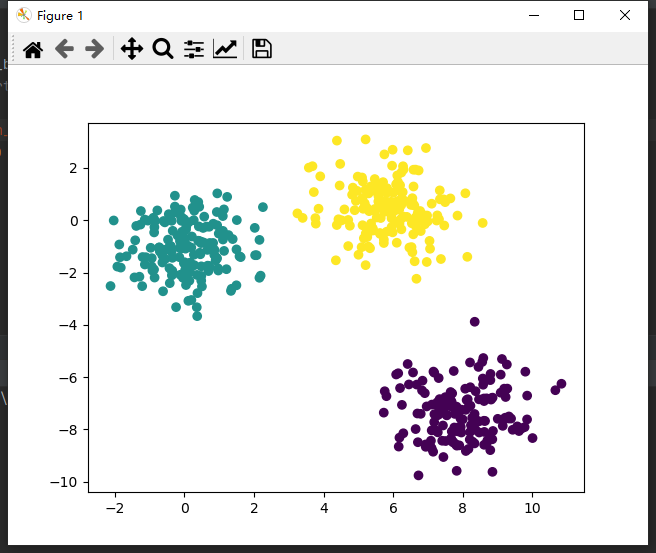

K-means算法的作用就是将数据划分成K个簇，每个簇高度相关，即离所在簇的质心是最近的。
下面将简介K-means算法原理步骤。

算法原理

1. 随机选取K个质心

随机3个点为质心（红黄蓝），淡蓝色为数据。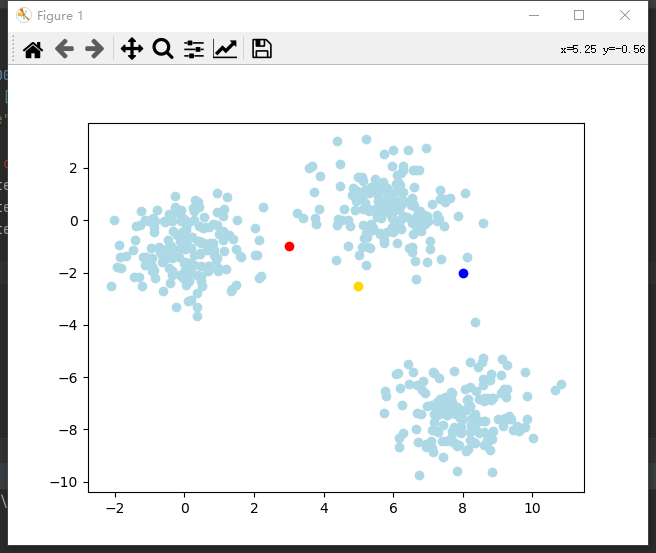

附可视化代码：

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# 生成数据集：500个点，二维特征，3个质心
x, y = make_blobs(n_samples=500, n_features=2, centers=3, random_state=20220929)
plt.scatter(x[:,0], x[:,1], color="lightblue")# 随机
center =[[3,-1],[5,-2.5],[8,-2]]
colors =["red","gold","blue"]
plt.scatter(center[0][0], center[0][1], color=colors[0])
plt.scatter(center[1][0], center[1][1], color=colors[1])
plt.scatter(center[2][0], center[2][1], color=colors[2])
plt.show()

1. 计算每个数据到各质心距离

一般使用欧氏距离来计算，为了便于展示，取特征维数为2，即

      (
     
     
      
       x
      
      
       1
      
     
     
      −
     
     
      
       x
      
      
       2
      
     
     
      
       )
      
      
       2
      
     
     
      +
     
     
      (
     
     
      
       y
      
      
       1
      
     
     
      −
     
     
      
       y
      
      
       2
      
     
     
      
       )
      
      
       2
      
     
    
   
  
  
   \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}
  
 
(x1​−x2​)2+(y1​−y2​)2​

def_distance(v1, v2):# 不开根号节省算力，效果一致return np.sum(np.square(v1-v2))

1. 将数据分到最近质心的簇

    dist = np.zeros((500,3),float)# 距离
    c =[3]# 3个簇for i inrange(500):
        mx =-1.# 最近值
        idx =0#最近簇for j inrange(3):
            dist[i][j]= _distance(x[i], center[j])if mx > dist[i][j]or mx ==-1.:
                mx = dist[i][j]
                idx = j
        # 设置透明度，以区分质心    
        plt.scatter(x[i][0], x[i][1], color=colors[idx], alpha=0.2)
        c[idx].append(i)  
    plt.show()

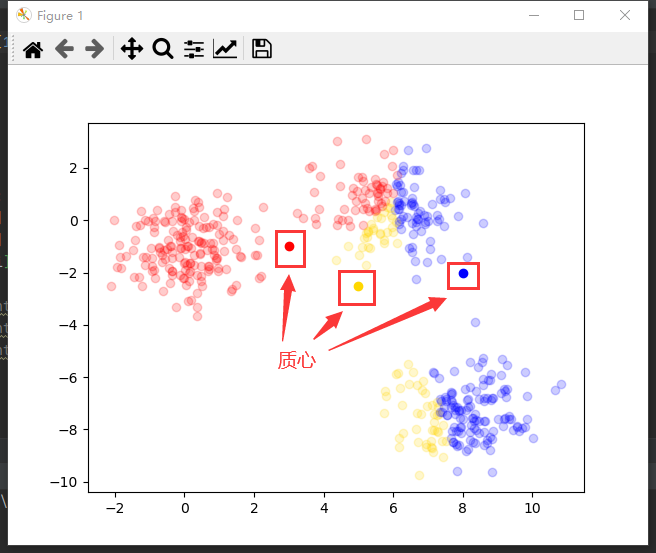
1. 根据各簇数据更新质心

     c
    
    
     j
    
   
   
    =
   
   
    
     1
    
    
     
      ∣
     
     
      
       c
      
      
       j
      
     
     
      ∣
     
    
   
   
    
     ∑
    
    
     
      x
     
     
      ∈
     
     
      
       c
      
      
       j
      
     
    
   
   
    x
   
   
   
   c_j=\frac{1}{\left|c_j\right|}\sum_{x\in c_j}x
   

   cj​=∣cj​∣1​∑x∈cj​​x

其中

     c
    
    
     j
    
   
  
  
   c_j
  
 
cj​表示第

 
  
   
    j
   
  
  
   j
  
 
j个质心，也就是计算属于当前簇数据的均值作为新的质心。即K均值算法名称由来。

当平均误差和SSE越小越接近质心，由推导得质心取数据均值时，SSE最小。

比如数据[[1, 2], [3, 4]]属于同一个簇，则更新簇中心为[2, 3]。

# 更新质心for i inrange(3):
        sum_x =0.
        sum_y =0.for j inrange(len(c[i])):
            sum_x += x[c[i][j]][0]
            sum_y += x[c[i][j]][1]
        center[i]=[sum_x/len(c[i]), sum_y/len(c[i])]
    plt.scatter(center[0][0], center[0][1], color=colors[0])
    plt.scatter(center[1][0], center[1][1], color=colors[1])
    plt.scatter(center[2][0], center[2][1], color=colors[2])
    plt.show()

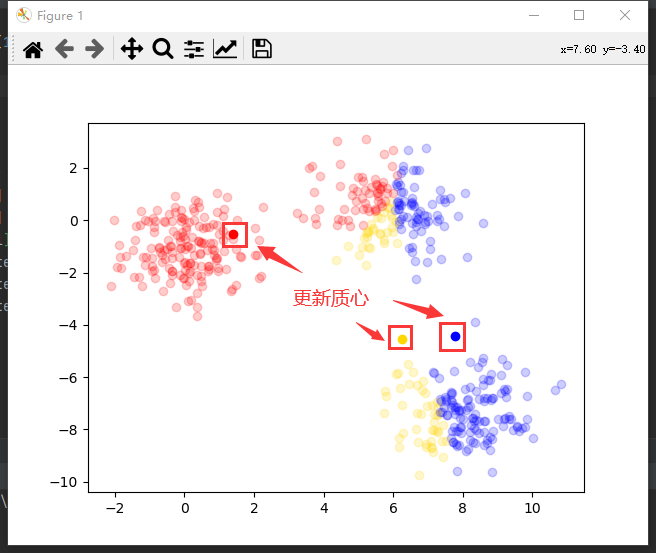
（插播反爬信息 ）博主CSDN地址：https://wzlodq.blog.csdn.net/

1. 重复2-4步直到收敛

     ∑
    
    
     
      i
     
     
      =
     
     
      1
     
    
    
     n
    
   
   
    a
   
   
    r
   
   
    g
   
   
    m
   
   
    i
   
   
    n
   
   
    ∣
   
   
    ∣
   
   
    
     x
    
    
     i
    
   
   
    −
   
   
    
     c
    
    
     i
    
   
   
    ∣
   
   
    ∣
   
   
   
   \sum_{i=1}^n argmin||x_i-c_i ||
   

   ∑i=1n​argmin∣∣xi​−ci​∣∣

计算当前聚类的平方差，循环退出条件是取得最小的平方差，也就是质心不再改变的时候。最终质心一定是确定的，不会陷入死循环。

随着循环次数逐渐收敛，不难证第1步随机的初始质心对结果无影响，即使得K-means算法具有普遍适用性。

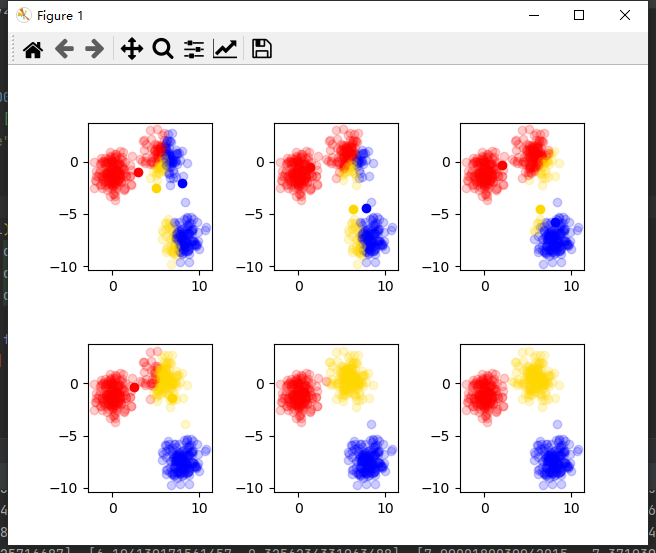
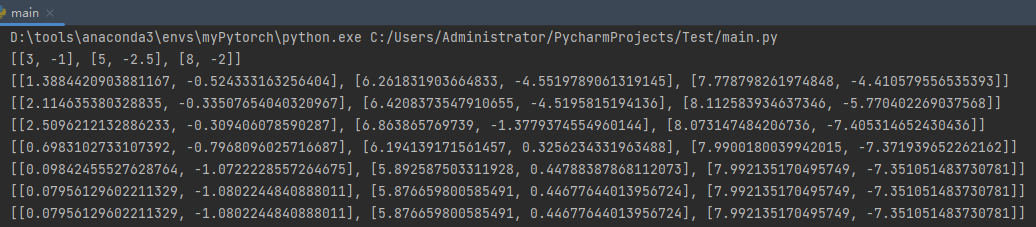
可以看出，第六次更新后聚类相同，数据收敛。
大家可以尝试修改初始质心，查看结果是否一致。

sklearn库调用

上面手动复现了K-means代码的实现，但其实sklearn库有相应的封装函数，本节介绍其调用。

sklearn.cluster.KMeans

，主要参数：

• n_clusters：k值，质心数，默认8
• max_iter : int, default：最大迭代次数
• tol：质心的变化率小于此值时结束，默认1e-4
• random_state：随机种子

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

if __name__ =="__main__":# 数据
    x, y = make_blobs(n_samples=500, n_features=2, centers=3, random_state=20220929)# 创建KMeans对象
    km = KMeans(n_clusters=3, random_state=20220929)# 训练模型
    km.fit(x)# 测试
    predict = km.predict(x)# 可视化
    plt.scatter(x[:,0], x[:,1], c=predict)
    plt.show()

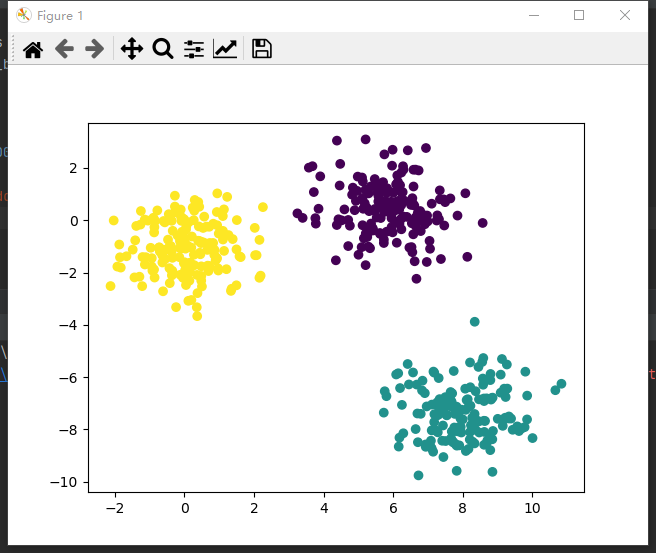
用过都说好(～￣▽￣)～

K的取值

最后还有一个问题，就是K是用户指定的，那又该怎么确定K值呢？

站在巨人的肩膀上，主要有两种方法：手肘法和轮廓系数法。

1. 手肘法

    S
   
   
    S
   
   
    E
   
   
    =
   
   
    
     ∑
    
    
     
      i
     
     
      =
     
     
      1
     
    
    
     k
    
   
   
    
     ∑
    
    
     
      p
     
     
      ∈
     
     
      
       C
      
      
       i
      
     
    
   
   
    ∣
   
   
    p
   
   
    −
   
   
    
     m
    
    
     i
    
   
   
    
     ∣
    
    
     2
    
   
   
   
   SSE=\sum_{i=1}^k\sum_{p\in C_i}|p-m_i|^2
   

   SSE=∑i=1k​∑p∈Ci​​∣p−mi​∣2

     C
    
    
     i
    
   
   
   
   C_i
   

   Ci​表示第

    i
   
   
   
   i
   

   i个簇，

     m
    
    
     i
    
   
   
   
   m_i
   

   mi​表示第

    i
   
   
   
   i
   

   i个簇的质心，

    p
   
   
   
   p
   

   p是数据样本点。

根据误差平方和SSE来选择K值，但并不是选SSE最小时对应的K，而是选SSE突然变小时的K，如下图，K应选3，图似手肘故得名。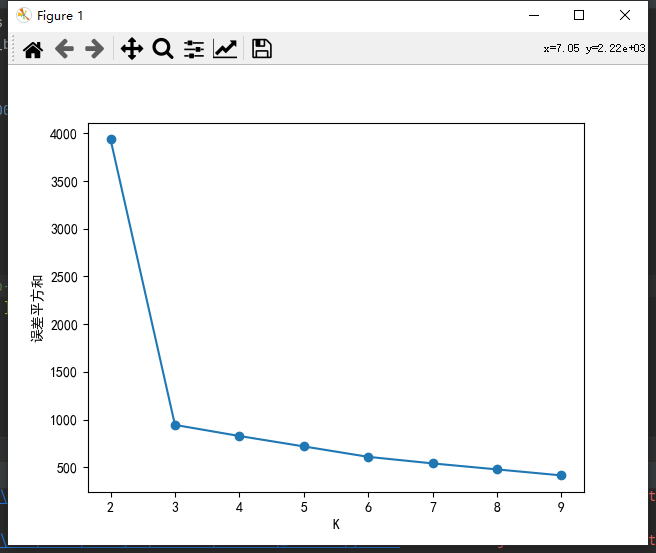

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

if __name__ =="__main__":
    x, y = make_blobs(n_samples=500, n_features=2, centers=3, random_state=20220929)
    SSE =[]for k inrange(2,10):
        km = KMeans(n_clusters=k)
        km.fit(x)
        SSE.append(km.inertia_)
    plt.xlabel('K')
    plt.ylabel('误差平方和')
    plt.plot(range(2,10), SSE,'o-')
    plt.rcParams['font.sans-serif']=['SimHei']
    plt.show()

1. 轮廓系数法

    S
   
   
    =
   
   
    
     
      b
     
     
      −
     
     
      a
     
    
    
     
      m
     
     
      a
     
     
      x
     
     
      (
     
     
      a
     
     
      ,
     
     
      b
     
     
      )
     
    
   
   
   
   S=\frac{b-a}{max(a,b)}
   

   S=max(a,b)b−a​

    a
   
   
   
   a
   

   a是到同簇中其它样本的平均距离，表示内聚度。

    b
   
   
   
   b
   

   b是到其他簇中所有样本的平均距离，表示分离度。

考虑内聚度和分离度两个因素，计算轮廓系数（Silhouette Coefficient）S，S越接近1则聚类效果越好。如下图，K=3时，S最接近1。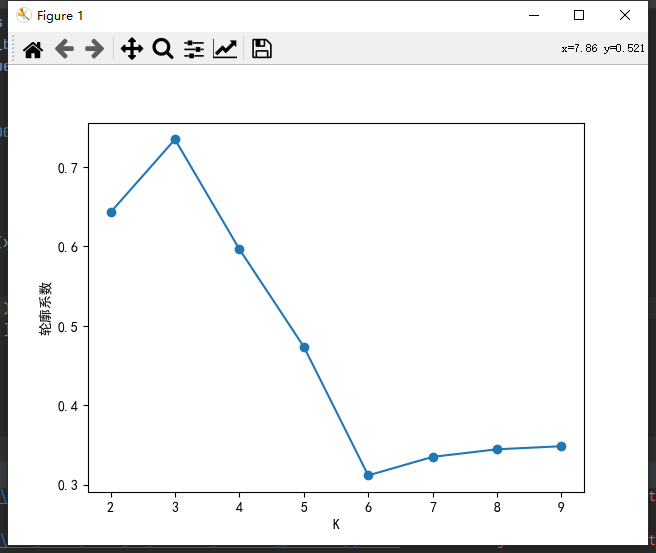

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_score

if __name__ =="__main__":
    x, y = make_blobs(n_samples=500, n_features=2, centers=3, random_state=20220929)
    S =[]for k inrange(2,10):
        km = KMeans(n_clusters=k)
        km.fit(x)
        S.append(silhouette_score(x, km.labels_))
    plt.xlabel('K')
    plt.ylabel('轮廓系数')
    plt.plot(range(2,10), S,'o-')
    plt.rcParams['font.sans-serif']=['SimHei']
    plt.show()

原创不易，请勿转载（本不富裕的访问量雪上加霜 ）
博主首页：https://wzlodq.blog.csdn.net/
来都来了，不评论两句吗👀
如果文章对你有帮助，记得一键三连❤