本文首次在公众号【零妖阁】上发表，为了方便阅读和分享，我们将在其他平台进行自动同步。由于不同平台的排版格式可能存在差异，为了避免影响阅读体验，建议如有排版问题，可前往公众号查看原文。感谢您的阅读和支持！
DoA 估计是指根据天线阵列的接收信号估计出单个或多个信号源的方位信息。由于激励信号和方向图之间存在傅里叶关系，DoA 估计也可以等效为谱估计问题。
多重信号分类（Mutiple Signal Classification）算法，简称 MUSIC 算法，是一种常用的 DoA 估计方法。它的基本思想是将任意阵列输出数据的协方差矩阵进行特征分解，从而得到与信号分量相对应的信号子空间和与信号分量相正交的噪声子空间。
信号模型
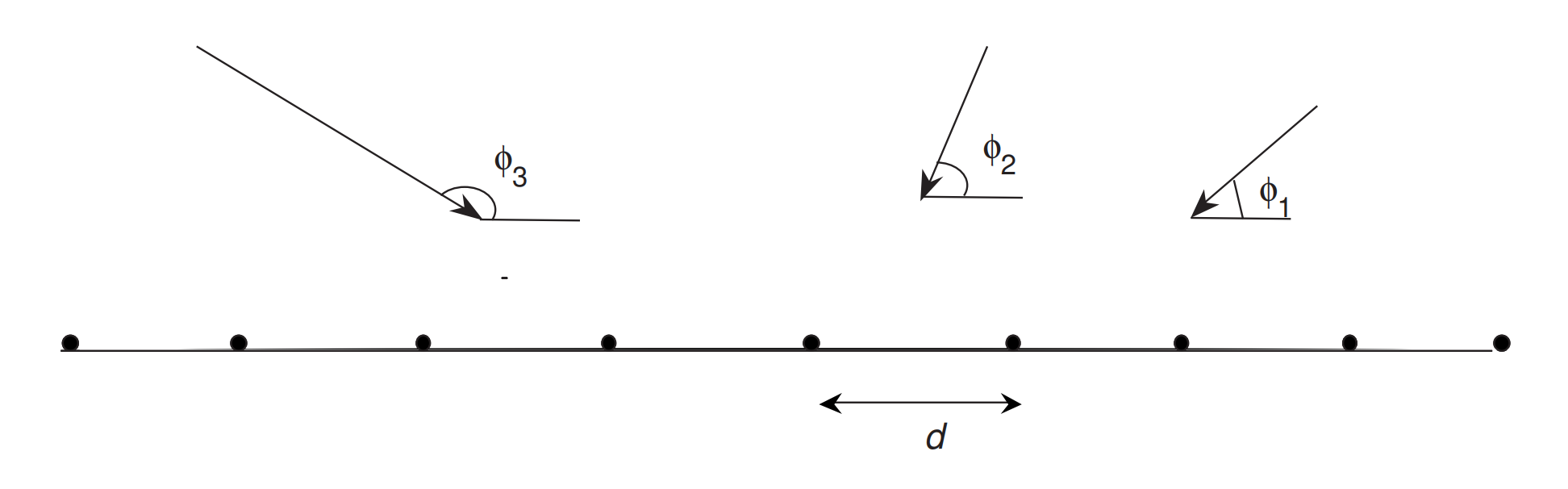
假设空间中存在
M
M
M 个不同方向的信号，入射到由
N
N
N 个天线单元构成的**均匀直线阵**上。第
i
i
i 个信号源的方向为
ϕ
i
\phi_i
ϕi（
i
=
1
,
…
,
M
i = 1,\dots,M
i=1,…,M），第
i
i
i 个信号源的信号为
α
i
(
t
)
\alpha_i(t)
αi(t)。**假设
M
<
N
M < N
M<N 。**
令第
n
n
n 个天线单元的**噪声**为
n
n
(
t
)
n_n(t)
nn(t)。在**窄带远场条件**下，第
n
n
n 个天线单元的输出信号
x
n
(
t
)
x_n(t)
xn(t) 可表示为
x
n
(
t
)
=
∑
i
=
1
M
α
i
(
t
)
e
j
k
z
n
sin
ϕ
i
+
n
n
(
t
)
=
∑
i
=
1
M
α
i
(
t
)
s
n
(
ϕ
i
)
+
n
n
(
t
)
\begin{aligned} x_n(t) &= \sum\limits_{i=1}^{M} \alpha_i(t) e^{jkz_n\sin\phi_i} + n_n(t) \\ &= \sum\limits_{i=1}^{M} \alpha_i(t) s_n(\phi_i) + n_n(t) \end{aligned}
xn(t)=i=1∑Mαi(t)ejkznsinϕi+nn(t)=i=1∑Mαi(t)sn(ϕi)+nn(t)
将
N
N
N 个天线的**输出信号**表示成向量形式
x
(
t
)
\bf x (t)
x(t)，则上式可归纳为
x
(
t
)
=
S
α
(
t
)
+
n
(
t
)
\mathbf{x}(t) = \mathbf{S} \mathbf{\alpha}(t) + \mathbf{n}(t)
x(t)=Sα(t)+n(t)
其中，
S
\mathbf{S}
S 为阵列的**流型矩阵**，矩阵规模为
N
×
M
N\times M
N×M，具体可表示为
M
M
M
个不同方向对应的阵列导向矢量：
S
=
[
s
(
ϕ
1
)
,
s
(
ϕ
2
)
,
…
,
s
(
ϕ
M
)
]
\mathbf{S} = [\mathbf{s}(\phi_1), \mathbf{s}(\phi_2), \dots, \mathbf{s}(\phi_M) ]
S=[s(ϕ1),s(ϕ2),…,s(ϕM)]
由于
M
<
N
M < N
M<N，流型矩阵
S
\mathbf{S}
S 为**列满秩矩阵**，
R
a
n
k
(
S
)
=
M
\mathrm{Rank}(\mathbf{S}) = M
Rank(S)=M。
MUSIC 算法思想
假设不同信号源的信号之间是相互正交的，噪声与信号之间是正交的，则**阵列输出信号
x
(
t
)
\mathbf x(t)
x(t) 的协方差矩阵**为
R
=
E
[
x
(
t
)
x
(
t
)
H
]
=
E
[
S
α
(
t
)
α
(
t
)
H
S
H
+
n
(
t
)
n
(
t
)
H
]
=
S
A
S
H
+
σ
2
I
=
R
S
+
σ
2
I
\begin{aligned} \mathbf R &= \mathrm E [\mathbf x(t) \mathbf x(t)^H] \\ &= \mathrm E [\mathbf{S} \mathbf{\alpha}(t) \mathbf{\alpha}(t)^H \mathbf{S}^H + \mathbf{n}(t)\mathbf{n}(t)^H ] \\ &= \mathbf{S} \mathbf A \mathbf{S}^H + \sigma^2 \mathbf I \\ &= \mathbf{R}_S + \sigma^2 \mathbf I \\ \end{aligned}
R=E[x(t)x(t)H]=E[Sα(t)α(t)HSH+n(t)n(t)H]=SASH+σ2I=RS+σ2I
其中，
A
\mathbf A
A 为不同信号源之间的协方差矩阵，由于不同信号源之间是相互正交的，
A
\mathbf A
A 为**正定对角矩阵**：
A
=
[
E
[
∣
α
1
(
t
)
∣
2
]
…
…
…
…
E
[
∣
α
2
(
t
)
∣
2
]
…
…
…
…
…
…
…
…
…
E
[
∣
α
M
(
t
)
∣
2
]
]
\mathbf A = \left[\begin{matrix} &\mathrm E [\mathbf |\alpha_1(t)|^2] &\dots &\dots &\dots \\ &\dots &\mathrm E [\mathbf |\alpha_2(t)|^2] &\dots &\dots \\ &\dots &\dots &\dots &\dots \\ &\dots &\dots &\dots &\mathrm E [\mathbf |\alpha_M(t)|^2] \\ \end{matrix}\right]
A=E[∣α1(t)∣2]…………E[∣α2(t)∣2]………………………E[∣αM(t)∣2]
由于信号协方差矩阵
R
S
\mathbf R_S
RS 的规模为
N
×
N
N\times N
N×N，**秩为
M
M
M，**
R
S
\mathbf R_S
RS 存在
N
−
M
N - M
N−M 个**特征值为 0 的特征向量**，令这种特征向量为
q
m
\mathbf q_m
qm，则
R
S
q
m
=
0
\mathbf R_S \mathbf q_m = 0
RSqm=0
⇒
S
A
S
H
q
m
=
0
\Rightarrow \mathbf{S} \mathbf A \mathbf{S}^H \mathbf q_m = 0
⇒SASHqm=0
⇒
q
m
H
S
A
S
H
q
m
=
0
\Rightarrow \mathbf q_m^H \mathbf{S} \mathbf A \mathbf{S}^H \mathbf q_m = 0
⇒qmHSASHqm=0
⇒
S
H
q
m
=
0
\Rightarrow \mathbf{S}^H \mathbf q_m = 0
⇒SHqm=0
上述推论说明，
R
S
\mathbf R_S
RS 的特征值为 0 时对应的特征向量
q
m
\mathbf q_m
qm 与信号源对应的
M
M
M 个导向矢量均**正交**。
令
R
S
\mathbf R_S
RS 的
N
−
M
N-M
N−M 个特征值为 0 时对应的特征向量构成矩阵 $\mathbf Q_n $，其规模为
N
×
(
N
−
M
)
N \times (N-M)
N×(N−M)，则
S
H
Q
n
=
0
\mathbf{S}^H \mathbf Q_n = 0
SHQn=0
则 MUSIC 算法的谱估计公式为
P
M
U
S
I
C
(
ϕ
)
=
1
∣
∣
Q
n
H
s
(
ϕ
)
∣
∣
2
P_{\mathrm{MUSIC}}(\phi) = \frac{1}{|| \mathbf Q_n^H \mathbf s(\phi) ||^2}
PMUSIC(ϕ)=∣∣QnHs(ϕ)∣∣21
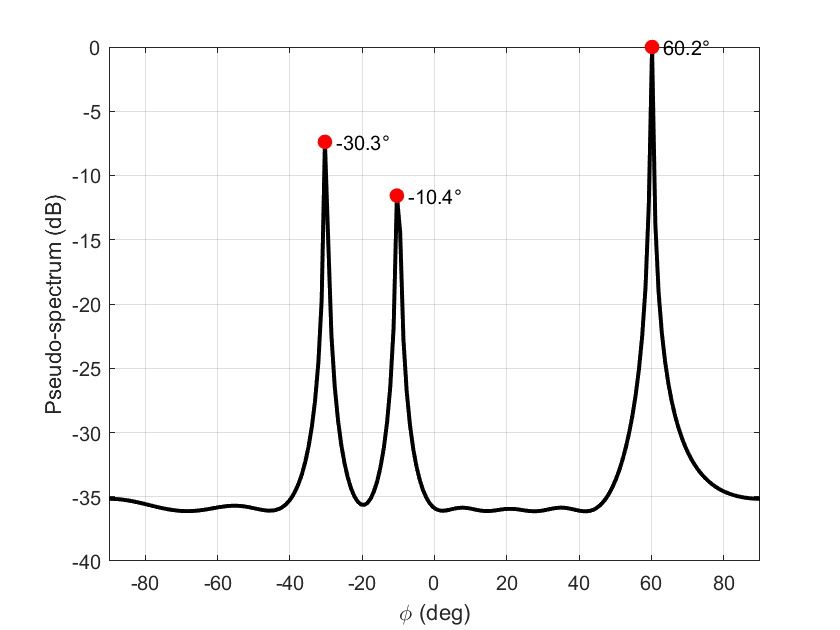
当上式中的
ϕ
\phi
ϕ 与信号源方向相同时，分母为零，此时 MUSIC 谱估计为无穷大。因此，**MUSIC 谱估计的尖峰数目与信源数目相同，尖峰对应的方向即为信号源的方向**。
如何根据阵列输出信号
x
\mathbf x
x 计算
Q
n
\mathbf Q_n
Qn ？
通过记录多组阵列输出信号快拍，可以计算出输出信号协方差矩阵的近似值
R
=
1
K
∑
k
=
1
K
x
k
x
k
H
\mathbf R = \frac{1}{K} \sum\limits_{k=1}^K \mathbf x_k \mathbf x_k^H
R=K1k=1∑KxkxkH
那么，如何根据输出信号的协方差矩阵
R
\mathbf R
R 估计出信号协方差矩阵
R
S
\mathbf R_S
RS 对应的特征值为 0 的特征向量矩阵
Q
n
\mathbf Q_n
Qn 呢？
对于
R
S
\mathbf R_S
RS 的任意特征向量
q
m
∈
Q
\mathbf q_m \in \mathbf Q
qm∈Q ，有
R
S
q
m
=
λ
m
q
m
\mathbf R_S \mathbf q_m = \lambda_m \mathbf q_m
RSqm=λmqm
⇒
R
q
m
=
R
S
q
m
+
σ
2
I
q
m
=
(
λ
m
+
σ
2
)
q
m
\begin{aligned} \Rightarrow \mathbf R \mathbf q_m &= \mathbf R_S \mathbf q_m + \sigma^2 \mathbf I \mathbf q_m \\ &= (\lambda_m + \sigma^2)\mathbf q_m \end{aligned}
⇒Rqm=RSqm+σ2Iqm=(λm+σ2)qm
因此，**信号协方差矩阵
R
S
\mathbf R_S
RS 的特征值
λ
m
\lambda_m
λm 对应的特征向量与输出信号协方差矩阵
R
\mathbf R
R 的特征值
λ
m
+
σ
2
\lambda_m+\sigma^2
λm+σ2 对应的特征向量相同**。
因此，
R
\mathbf R
R 的特征分解可表示为
R
=
Q
(
Λ
+
σ
2
I
)
Q
H
=
Q
[
λ
1
+
σ
2
0
…
0
0
…
0
0
λ
2
+
σ
2
…
0
0
…
0
…
…
…
…
…
…
…
0
0
…
λ
M
+
σ
2
0
…
0
0
0
…
0
σ
2
…
0
…
…
…
…
…
…
…
0
0
…
0
0
…
σ
2
]
Q
H
\begin{aligned} \mathbf R &= \mathbf Q (\mathbf \Lambda + \sigma^2 \mathbf I) \mathbf Q^H \\ &= \mathbf Q \left[\begin{matrix} &\lambda_1 + \sigma^2 &0 &\dots &0 &0 &\dots &0 \\ &0 &\lambda_2 + \sigma^2 &\dots &0 &0 &\dots &0 \\ &\dots &\dots &\dots &\dots &\dots &\dots &\dots \\ &0 &0 &\dots &\lambda_M + \sigma^2 &0 &\dots &0 \\ &0 &0 &\dots &0 &\sigma^2 &\dots &0 \\ &\dots &\dots &\dots &\dots &\dots &\dots &\dots \\ &0 &0 &\dots &0 &0 &\dots &\sigma^2 \\ \end{matrix}\right] \mathbf Q^H \end{aligned}
R=Q(Λ+σ2I)QH=Qλ1+σ20…00…00λ2+σ2…00…0…………………00…λM+σ20…000…0σ2…0…………………00…00…σ2QH
上式表明，**将输出信号矩阵
R
\mathbf R
R 进行特征分解，得到的
N
−
M
N-M
N−M 个较小且相等的特征值对应的特征向量即可构成
Q
n
\mathbf Q_n
Qn。**
MATLAB 仿真
clc; clear; close all;%% 参数设置%%% 工作频率
c =3e8;
freq =10e9;
lambda = c/freq;% 波长
k =2*pi/lambda;% 波数%%% 阵列参数
N =10;% 阵元数量
d =0.5*lambda;% 阵元间隔
z =(0:d:(N-1)*d)';% 阵元坐标分布%%% 信号源参数
phi =[-10,-30,60]'*pi/180;% 来波方向
M =length(phi);% 信号源数目%%% 仿真参数
SNR =10;% 信噪比(dB)
K =1000;% 采样点数%% 阵列接收信号仿真模拟
S =exp(1j*k*z*sin(phi'));% 流型矩阵
Alpha =randn(M, K);% 输入信号
X = S*Alpha;% 阵列接收信号
X1 =awgn(X, SNR,'measured');% 加载高斯白噪声%% MUSIC 算法%%% 阵列接收信号的协方差矩阵的特征分解
R = X1*X1'/K;% 阵列接收信号的协方差矩阵[EV, D]=eig(R);% 特征值分解
EVA =diag(D);% 提取特征值[EVA, I]=sort(EVA,'descend');% 降序排序
Q =EV(:, I);% 特征向量构成的矩阵
Q_n =Q(:, M+1:N);% 噪声子空间%%% 计算MUSIC谱估计函数
phi_list =linspace(-pi/2,pi/2,200)';
S1 =exp(1j*k*z*sin(phi_list'));% 不同方向对应的流型矢量构成矩阵
P_MUSIC =1./sum(abs(Q_n'*S1).^2);% MUSIC 谱估计公式%%% 转换为dB
P_MUSIC =abs(P_MUSIC);
P_MUSIC_max =max(P_MUSIC);
P_MUSIC_dB =10*log10(P_MUSIC/P_MUSIC_max);%%% 提取信号源方向[P_peaks, P_peaks_idx]=findpeaks(P_MUSIC_dB);% 提取峰值[P_peaks, I]=sort(P_peaks,'descend');% 峰值降序排序
P_peaks_idx =P_peaks_idx(I);
P_peaks =P_peaks(1:M);% 提取前M个
P_peaks_idx =P_peaks_idx(1:M);
phi_e =phi_list(P_peaks_idx)*180/pi;% 估计方向disp('信号源估计方向为：');disp(phi_e);%%% 绘图
figure;plot(phi_list*180/pi, P_MUSIC_dB,'k','Linewidth',2);xlabel('\phi (deg)');ylabel('Pseudo-spectrum (dB)');axis([-90,90,-40,0]);
grid on;
hold on;plot(phi_e, P_peaks,'r.','MarkerSize',25);
hold on;for idx =1:M
text(phi_e(idx)+3,P_peaks(idx),sprintf('%0.1f°',phi_e(idx)));end
参考文献
[1] 王永良. 空间谱估计理论与算法[M]. 清华大学出版社, 2004.
[2] 张小飞, 陈华伟, 仇小锋. 阵列信号处理及MATLAB实现[M]. 电子工业出版社, 2015.
标签：
算法
本文转载自: https://blog.csdn.net/fengyanlover/article/details/129472902
版权归原作者 零妖阁 所有， 如有侵权，请联系我们删除。
版权归原作者 零妖阁 所有， 如有侵权，请联系我们删除。