SM2算法是国家密码管理局于2010年12月颁布的中国商用公钥密码标准算法。SM2基于椭圆曲线离散对数问题,计算复杂度是指数级(暂未发现亚指数级或多项式级的计算方法),相较于广泛应用的RSA公钥密码算法,在同等安全程度要求下,SM2所需密钥长度小、处理速度快。由于SM2在安全性、运算性能等方面都优于RSA算法,且具有自主知识产权,我国计划在商用密码体系中用SM2替换RSA算法。
椭圆曲线密码(ECC)的安全性明显强于RSA,参考下图:
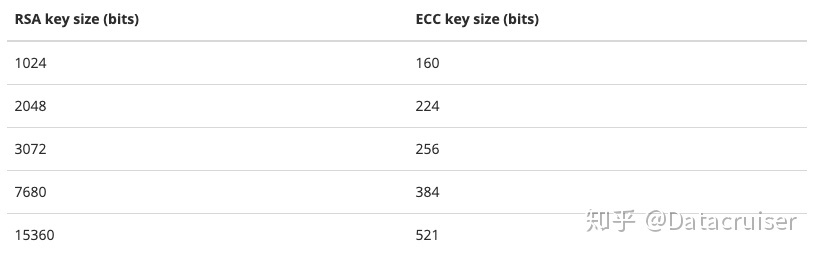
采用Python语言编写的国密工具包主要是gmssl-python库和snowland-smx-python(pysmx)库,二者较为完整地实现了SM2、SM3、SM4等国密算法。本工具包涉及的散列运算使用了pysmx库的SM3算法,pysmx库对SM3算法的实现高效而优雅,在此向pysmx库的作者致以诚挚的敬意和感谢!
相较于现有Python国密算法工具包的SM2模块,本工具包的优势主要体现在以下3个方面:
1. 首次开源SM2密钥协商算法。gmssl库和pysmx库仅实现了SM2签名和验证、加密和解密算法,没有实现SM2密钥协商算法,互联网上也未找到实现SM2密钥协商算法的Python代码,故本工具包是首次在互联网上开源SM2密钥协商算法的Python代码。
2. 算法实现更为健壮和完整。gmssl库和pysmx库中的椭圆曲线点乘算法仅能输入有限域内的乘数(否则报错),所实现的SM2签名/验证算法不包含标准要求的Z值计算和Hash变换,除核心算法(密钥生成、签名、验证、加密、解密等)之外还缺少标准描述的一些辅助算法,gmssl库仅能输入bytes类型消息;本工具包的点乘算法能够输入任意自然数作为乘数并保证正确性,SM2签名/验证算法完整实现了Z值计算和Hash变换,除核心算法之外还实现了标准描述的一些重要辅助函数(如公钥验证、椭圆曲线系统参数验证等)。
3. 性能更佳。本工具包通过采用更高效的点乘算法、减少数据类型转换、充分运用算术运算加速技巧等途径,明显提高了计算效率。以SM2算法耗时的主要来源——椭圆曲线点乘运算为例进行测试,同等条件下本工具包的平均耗时约为gmssl库的35.5%、pysmx库的61.8%,实际运行签名与验证、加解密等算法同样具备上述幅度的性能优势。

上图中的前三个算法是本工具包实现的(具体描述参考国密局2010年SM2文档,下有链接),实测算法2性能最好,默认用的算法2。
对于需应用国密SM2算法的Python项目,可直接调用本工具包实现SM2数字签名与验证、加解密以及密钥协商等功能,也可基于本工具包提供的椭圆曲线运算相关函数自行设计算法和协议。
参考文献:
- 国家密码管理局关于发布《SM2椭圆曲线公钥密码算法》公告[EB/OL].(2010-12-17) [2022-02-20].https://sca.gov.cn/sca/xwdt/2010-12/17/content_1002386.shtml.
- GMSSL[EB/OL].(2020-12-09) [2022-02-20].https://github.com/duanhongyi/gmssl.
- snowland-smx[EB/OL].(2021-01-27) [2022-02-20].https://gitee.com/snowlandltd/ snowland-smx-python.
“没有网络安全,就没有国家安全。”让我们共同努力,推动国密算法更深层次、更广泛的研究和应用,为国家网络信息安全和自主化尽绵薄之力。
是否觉得看到上面一句就结束了?O(∩_∩)O
代码分三个部分,第一部分是椭圆曲线基础运算封装的类,第二部分是SM2封装的类,第三部分是测试代码。最简单而安全的密钥协商,可以用里面的ECDH,运行很快,当然SM2更安全!同时致敬DH算法,为信息网络安全耕耘已近半个世纪!几种密钥协商算法的运行时间如下图所示:

上图结果均不包括通信开销,其中ECDH和SM2用的是SM2 GB(GB/T 32918.5-2017,信息安全技术 SM2椭圆曲线公钥密码算法 第5部分:参数定义)规定的椭圆曲线参数(与参考文献1《SM2椭圆曲线公钥密码算法》中推荐的参数是一样的),这也是本工具包默认使用的参数。
测试代码按照参考文献1(国密局2010年《SM2椭圆曲线公钥密码算法》)的参数,复现了其结果,说明代码实现是标准且正确的。由于要复现结果,测试代码调用函数的时候输入了固定参数,其实好多参数是不用输入的,不输入就会使用SM2默认参数,或者随机数。
废话不多说了,代码中有详尽注释。SM2怎么用?照着测试代码用就行!
下面是完整代码(是否完整?能不能跑?一试便知!)。
import random
import time
import math
import numpy as np
from pysmx.SM3 import digest as sm3
# 小素数列表,加快判断素数速度
small_primes = np.array([2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,
43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109,
113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191,
193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269,
271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353,
359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439,
443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523,
541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617,
619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709,
719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811,
821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907,
911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997])
def is_prime(num):
# 排除0,1和负数
if num < 2:
return False
# 排除小素数的倍数
for prime in small_primes:
if num % prime == 0:
return False
# 未分辨出来的大整数用rabin算法判断
return rabin_miller(num)
def rabin_miller(num):
s = num - 1
t = 0
while s & 1 == 0:
s >>= 1
t += 1
for trials in range(5):
a = random.randrange(2, num - 1)
v = pow(a, s, num)
if v != 1:
i = 0
while v != (num - 1):
if i == t - 1:
return False
else:
i = i + 1
v = v * v % num
return True
# 将字节转换为int
def to_int(byte):
return int.from_bytes(byte, byteorder='big')
# 转换为bytes,第二参数为字节数(可不填)
def to_byte(x, size=None):
if isinstance(x, int):
if size is None: # 计算合适的字节数
size = 0
tmp = x >> 64
while tmp:
size += 8
tmp >>= 64
tmp = x >> (size << 3)
while tmp:
size += 1
tmp >>= 8
elif x >> (size << 3): # 指定的字节数不够则截取低位
x &= (1 << (size << 3)) - 1
return x.to_bytes(size, byteorder='big')
elif isinstance(x, str):
x = x.encode()
if size != None and len(x) > size: # 超过指定长度
x = x[:size] # 截取左侧字符
return x
elif isinstance(x, bytes):
if size != None and len(x) > size: # 超过指定长度
x = x[:size] # 截取左侧字节
return x
elif isinstance(x, tuple) and len(x) == 2 and type(x[0]) == type(x[1]) == int:
# 针对坐标形式(x, y)
return to_byte(x[0], size) + to_byte(x[1], size)
return bytes(x)
# 将列表元素转换为bytes并连接
def join_bytes(data_list):
return b''.join([to_byte(i) for i in data_list])
# 求最大公约数
def gcd(a, b):
return a if b == 0 else gcd(b, a % b)
# 求乘法逆元过程中的辅助递归函数
def get_(a, b):
if b == 0:
return 1, 0
x1, y1 = get_(b, a % b)
x, y = y1, x1 - a // b * y1
return x, y
# 求乘法逆元
def get_inverse(a, p):
# return pow(a, p-2, p) # 效率较低、n倍点的时候两种计算方法结果会有不同
if gcd(a, p) == 1:
x, y = get_(a, p)
return x % p
return 1
def get_cpu_time():
return time.perf_counter()
# 密钥派生函数(从一个共享的秘密比特串中派生出密钥数据)
# SM2第3部分 5.4.3
# Z为bytes类型
# klen表示要获得的密钥数据的比特长度(8的倍数),int类型
# 输出为bytes类型
def KDF(Z, klen):
ksize = klen >> 3
K = bytearray()
for ct in range(1, math.ceil(ksize / HASH_SIZE) + 1):
K.extend(sm3(Z + to_byte(ct, 4)))
return K[:ksize]
# 计算比特位数
def get_bit_num(x):
if isinstance(x, int):
num = 0
tmp = x >> 64
while tmp:
num += 64
tmp >>= 64
tmp = x >> num >> 8
while tmp:
num += 8
tmp >>= 8
x >>= num
while x:
num += 1
x >>= 1
return num
elif isinstance(x, str):
return len(x.encode()) << 3
elif isinstance(x, bytes):
return len(x) << 3
return 0
# 椭圆曲线密码类(实现一般的EC运算,不局限于SM2)
class ECC:
def __init__(self, p, a, b, n, G, h=None):
self.p = p
self.a = a
self.b = b
self.n = n
self.G = G
if h:
self.h = h
self.O = (-1, -1) # 定义仿射坐标下无穷远点(零点)
# 预先计算Jacobian坐标两点相加时用到的常数
self._2 = get_inverse(2, p)
self.a_3 = (a + 3) % p
# 椭圆曲线上两点相加(仿射坐标)
# SM2第1部分 3.2.3.1
# 仅提供一个参数时为相同坐标点相加
def add(self, P1, P2=None):
x1, y1 = P1
if P2 is None or P1 == P2: # 相同坐标点相加
# 处理无穷远点
if P1 == self.O:
return self.O
# 计算斜率k(k已不具备明确的几何意义)
k = (3 * x1 * x1 + self.a) * get_inverse(2 * y1, self.p) % self.p
# 计算目标点坐标
x3 = (k * k - x1 - x1) % self.p
y3 = (k * (x1 - x3) - y1) % self.p
else:
x2, y2 = P2
# 处理无穷远点
if P1 == self.O:
return P2
if P2 == self.O:
return P1
if x1 == x2:
return self.O
# 计算斜率k
k = (y2 - y1) * get_inverse(x2 - x1, self.p) % self.p
# 计算目标点坐标
x3 = (k * k - x1 - x2) % self.p
y3 = (k * (x1 - x3) - y1) % self.p
return x3, y3
# 椭圆曲线上的点乘运算(仿射坐标)
def multiply(self, k, P):
# 判断常数k的合理性
assert type(k) is int and k >= 0, 'factor value error'
# 处理无穷远点
if k == 0 or P == self.O:
return self.O
if k == 1:
return P
elif k == 2:
return self.add(P)
elif k == 3:
return self.add(P, self.add(P))
elif k & 1 == 0: # k/2 * P + k/2 * P
return self.add(self.multiply(k >> 1, P))
elif k & 1 == 1: # P + k/2 * P + k/2 * P
return self.add(P, self.add(self.multiply(k >> 1, P)))
# 输入P,返回-P
def minus(self, P):
Q = list(P)
Q[1] = -Q[1]
return tuple(Q)
# Jacobian加重射影坐标下两点相加
# SM2第1部分 A.1.2.3.2
# 输入点包含两项时为仿射坐标,三项为Jacobian加重射影坐标,两点坐标系可不同
# 两点相同时省略第二个参数
def Jacb_add(self, P1, P2=None):
if P2 is None or P1 == P2: # 相同点相加
# 处理无穷远点
if P1 == self.O:
return self.O
# 根据参数包含的项数判断坐标系(是仿射坐标则转Jacobian坐标)
x1, y1, z1 = P1 if len(P1) == 3 else (*P1, 1)
# t1 = 3 * x1**2 + self.a * pow(z1, 4, self.p)
# t2 = 4 * x1 * y1**2
# t3 = 8 * pow(y1, 4, self.p)
# x3 = (t1**2 - 2 * t2) % self.p
# y3 = (t1 * (t2 - x3) - t3) % self.p
# z3 = 2 * y1 * z1 % self.p
z3 = (y1 * z1 << 1) % self.p
if z3 == 0: # 处理无穷远点
return self.O
T2 = y1 * y1 % self.p
T4 = (T2 << 3) % self.p
T5 = x1 * T4 % self.p
T6 = z1 * z1 % self.p
T1 = (x1 + T6) * (x1 - T6) * 3 % self.p
T1 = (T1 + self.a_3 * T6 * T6) % self.p
T3 = T1 * T1 % self.p
T2 = T2 * T4 % self.p
x3 = (T3 - T5) % self.p
T4 = T5 + (T5 + self.p >> 1) - T3 if T5 & 1 else T5 + (T5 >> 1) - T3
T1 = T1 * T4 % self.p
y3 = (T1 - T2) % self.p
else: # 不同点相加
# 处理无穷远点
if P1 == self.O:
return P2
if P2 == self.O:
return P1
# 根据参数包含的项数判断坐标系(是仿射坐标则转Jacobian坐标)
x1, y1, z1 = P1 if len(P1) == 3 else (*P1, 1)
x2, y2, z2 = P2 if len(P2) == 3 else (*P2, 1)
if z2 != 1 and z1 != 1:
z1_2 = z1 * z1 % self.p
z2_2 = z2 * z2 % self.p
t1 = x1 * z2_2 % self.p
t2 = x2 * z1_2 % self.p
t3 = t1 - t2
z3 = z1 * z2 * t3 % self.p
if z3 == 0: # 处理无穷远点
return self.O
t4 = y1 * z2 * z2_2 % self.p
t5 = y2 * z1 * z1_2 % self.p
t6 = t4 - t5
t7 = t1 + t2
t8 = t4 + t5
t3_2 = t3 * t3 % self.p
x3 = (t6 * t6 - t7 * t3_2) % self.p
t9 = (t7 * t3_2 - (x3 << 1)) % self.p
y3 = (t9 * t6 - t8 * t3 * t3_2) * self._2 % self.p
else: # 可简化计算
if z1 == 1: # 确保第二个点的z1=1
x1, y1, z1, x2, y2 = x2, y2, z2, x1, y1
T1 = z1 * z1 % self.p
T2 = y2 * z1 % self.p
T3 = x2 * T1 % self.p
T1 = T1 * T2 % self.p
T2 = T3 - x1
z3 = z1 * T2 % self.p
if z3 == 0: # 处理无穷远点
return self.O
T3 = T3 + x1
T1 = T1 - y1
T4 = T2 * T2 % self.p
T5 = T1 * T1 % self.p
T2 = T2 * T4 % self.p
T3 = T3 * T4 % self.p
T4 = x1 * T4 % self.p
x3 = T5 - T3 % self.p
T2 = y1 * T2 % self.p
T3 = T4 - x3
T1 = T1 * T3 % self.p
y3 = T1 - T2 % self.p
# T1 = z1 * z1 % self.p
# T3 = x2 * T1 % self.p
# T2 = T3 - x1
# z3 = z1 * T2 % self.p
# if z3 == 0: # 处理无穷远点
# return self.O
# T1 = (T1 * y2 * z1 - y1) % self.p
# T4 = T2 * T2 % self.p
# x3 = T1 * T1 - (T3 + x1) * T4 % self.p
# T1 = T1 * (x1 * T4 - x3) % self.p
# y3 = T1 - y1 * T2 * T4 % self.p
return x3, y3, z3
# Jacobian加重射影坐标下的点乘运算
# SM2第1部分 A.3
# 输入点包含两项时为仿射坐标,三项为Jacobian坐标
# conv=True时结果转换为仿射坐标,否则不转换
# algo表示选择的算法, r表示算法三(滑动窗法)的窗口值
def Jacb_multiply(self, k, P, conv=True, algo=2, r=5):
# 处理无穷远点
if k == 0 or P == self.O:
return self.O
# 仿射坐标转Jacobian坐标
# if len(P) == 2:
# P = (*P, 1)
# 算法一:二进制展开法
if algo == 1:
Q = P
for i in bin(k)[3:]:
Q = self.Jacb_add(Q)
if i == '1':
Q = self.Jacb_add(Q, P)
# 算法二:加减法
elif algo == 2:
h = bin(3 * k)[2:]
k = bin(k)[2:]
k = '0' * (len(h) - len(k)) + k
Q = P
minusP = self.minus(P)
for i in range(1, len(h) - 1):
Q = self.Jacb_add(Q)
if h[i] == '1' and k[i] == '0':
Q = self.Jacb_add(Q, P)
elif h[i] == '0' and k[i] == '1':
Q = self.Jacb_add(Q, minusP)
# 算法三:滑动窗法
# 当k为255/256位时,通过test_r函数测试,r=5复杂度最低
elif algo == 3:
k = bin(k)[2:]
l = len(k)
if r >= l: # 如果窗口大于k的二进制位数,则本算法无意义
return self.Jacb_multiply(int(k, 2), P, conv, 2)
# 保存P[j]值的字典
P_ = {1: P, 2: self.Jacb_add(P)}
for i in range(1, 1 << (r - 1)):
P_[(i << 1) + 1] = self.Jacb_add(P_[(i << 1) - 1], P_[2])
t = r
while k[t - 1] != '1':
t -= 1
hj = int(k[:t], 2)
Q = P_[hj]
j = t
while j < l:
if k[j] == '0':
Q = self.Jacb_add(Q)
j += 1
else:
t = min(r, l - j)
while k[j + t - 1] != '1':
t -= 1
hj = int(k[j:j + t], 2)
Q = self.Jacb_add(self.Jacb_multiply(1 << t, Q, False, 2), P_[hj])
j += t
return self.Jacb_to_affine(Q) if conv else Q
# Jacobian加重射影坐标转仿射坐标
# SM2第1部分 A.1.2.3.2
def Jacb_to_affine(self, P):
if len(P) == 2: # 已经是仿射坐标
return P
x, y, z = P
# 处理无穷远点
if z == 0:
return self.O
z_ = get_inverse(z, self.p) # z的乘法逆元
x2 = x * z_ * z_ % self.p
y2 = y * z_ * z_ * z_ % self.p
return x2, y2
# 判断是否为无穷远点(零点)
def is_zero(self, P):
if len(P) == 2: # 仿射坐标
return P == self.O
else: # Jacobian加重射影坐标
return P[2] == 0
# 判断是否为域Fp中的元素
# 可输入多个元素,全符合才返回True
def on_Fp(self, *x):
for i in x:
if 0 <= i < self.p:
pass
else:
return False
return True
# 判断是否在椭圆曲线上
def on_curve(self, P):
if self.is_zero(P):
return False
if len(P) == 2: # 仿射坐标
x, y = P
return y * y % self.p == (x * x * x + self.a * x + self.b) % self.p
else: # Jacobian加重射影坐标
x, y, z = P
return y * y % self.p == (x * x * x + self.a * x * pow(z, 4, self.p) + self.b * pow(z, 6, self.p)) % self.p
# 生成密钥对
# 返回值:d为私钥,P为公钥
# SM2第1部分 6.1
def gen_keypair(self):
d = random.randint(1, self.n - 2)
P = self.Jacb_multiply(d, self.G)
return d, P
# 公钥验证
# SM2第1部分 6.2.1
def pk_valid(self, P):
# 判断点P的格式
if P and len(P) == 2 and type(P[0]) == type(P[1]) == int:
pass
else:
self.error = '格式有误' # 记录错误信息
return False
# a) 验证P不是无穷远点O
if self.is_zero(P):
self.error = '无穷远点'
return False
# b) 验证公钥P的坐标xP和yP是域Fp中的元素
if not self.on_Fp(*P):
self.error = '坐标值不是域Fp中的元素'
return False
# c) 验证y^2 = x^3 + ax + b (mod p)
if not self.on_curve(P):
self.error = '不在椭圆曲线上'
return False
# d) 验证[n]P = O
if not self.is_zero(self.Jacb_multiply(self.n, P, False)):
self.error = '[n]P不是无穷远点'
return False
return True
# 确认目前已有公私钥对
def confirm_keypair(self):
if not hasattr(self, 'pk') or not self.pk_valid(self.pk) or self.pk != self.Jacb_multiply(self.sk, self.G):
# 目前没有合格的公私钥对则生成
while True:
d, P = self.gen_keypair()
if self.pk_valid(P): # 确保公钥通过验证
self.sk, self.pk = d, P
return
# 国家密码管理局:SM2椭圆曲线公钥密码算法推荐曲线参数
SM2_p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
SM2_a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
SM2_b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
SM2_n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
SM2_Gx = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
SM2_Gy = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
PARA_SIZE = 32 # 参数长度(字节)
HASH_SIZE = 32 # sm3输出256位(32字节)
KEY_LEN = 128 # 默认密钥位数
# SM2类继承ECC
class SM2(ECC):
# 默认使用SM2推荐曲线参数
def __init__(self, p=SM2_p, a=SM2_a, b=SM2_b, n=SM2_n, G=(SM2_Gx, SM2_Gy), h=None,
ID=None, sk=None, pk=None, genkeypair=True): # genkeypair表示是否自动生成公私钥对
if not h: # 余因子h默认为1
h = 1
ECC.__init__(self, p, a, b, n, G, h)
self.keysize = len(to_byte(n)) # 密钥长度(字节)
if type(ID) in (int, str): # 身份ID(数字或字符串)
self.ID = ID
else:
self.ID = ''
if sk and pk: # 如果提供的公私钥对通过验证,即使genkeypair=True也不会重新生成
self.sk = sk # 私钥(int [1,n-2])
self.pk = pk # 公钥(x, y)
self.confirm_keypair() # 验证该公私钥对,不合格则生成
elif genkeypair: # 自动生成合格的公私钥对
self.confirm_keypair()
# 预先计算用到的常数
if hasattr(self, 'sk'): # 签名时
self.d_1 = get_inverse(1 + self.sk, self.n)
# 椭圆曲线系统参数验证
# SM2第1部分 5.2.2
def para_valid(self):
# a) 验证q = p是奇素数
if not is_prime(self.p):
self.error = 'p不是素数' # 记录错误信息
return False
# b) 验证a、b、Gx和Gy是区间[0, p−1]中的整数
if not self.on_Fp(self.a, self.b, *self.G):
self.error = 'a、b或G坐标值不是域Fp中的元素'
return False
# d) 验证(4a^3 + 27b^2) mod p != 0
if (4 * self.a * self.a * self.a + 27 * self.b * self.b) % self.p == 0:
self.error = '(4a^3 + 27b^2) mod p = 0'
return False
# e) 验证Gy^2 = Gx^3 + aGx + b (mod p)
if not self.on_curve(self.G):
self.error = 'G不在椭圆曲线上'
return False
# f) 验证n是素数,n > 2^191 且 n > 4p^1/2
if not is_prime(self.n) or self.n <= 1 << 191 or self.n <= 4 * self.p ** 0.5:
self.error = 'n不是素数或n不够大'
return False
# g) 验证[n]G = O
if not self.is_zero(self.Jacb_multiply(self.n, self.G, False)):
self.error = '[n]G不是无穷远点'
return False
# i) 验证抗MOV攻击条件和抗异常曲线攻击条件成立(A.4.2.1)
B = 27 # MOV阈B
t = 1
for i in range(B):
t = t * self.p % self.n
if t == 1:
self.error = '不满足抗MOV攻击条件'
return False
# 椭圆曲线的阶N=#E(Fp)计算太复杂,未实现A.4.2.2验证
# Fp上的绝大多数椭圆曲线确实满足抗异常曲线攻击条件
return True
# 计算Z
# SM2第2部分 5.5
# ID为数字或字符串,P为公钥(不提供参数时返回自身Z值)
def get_Z(self, ID=None, P=None):
save = False
if not P: # 不提供参数
if hasattr(self, 'Z'): # 再次计算,返回曾计算好的自身Z值
return self.Z
else: # 首次计算自身Z值
ID = self.ID
P = self.pk
save = True
entlen = get_bit_num(ID)
ENTL = to_byte(entlen, 2)
Z = sm3(join_bytes([ENTL, ID, self.a, self.b, *self.G, *P]))
if save: # 保存自身Z值
self.Z = Z
return Z
# 数字签名
# SM2第2部分 6.1
# 输入:待签名的消息M、随机数k(不填则自动生成)、输出类型(默认bytes)、对M是否hash(默认是)
# 输出:r, s(int类型)或拼接后的bytes
def sign(self, M, k=None, outbytes=True, dohash=True):
if dohash:
M_ = join_bytes([self.get_Z(), M])
e = to_int(sm3(M_))
else:
e = to_int(to_byte(M))
while True:
if not k:
k = random.randint(1, self.n - 1)
# x1, y1 = self.multiply(k, self.G)
x1, y1 = self.Jacb_multiply(k, self.G)
r = (e + x1) % self.n
if r == 0 or r + k == self.n:
k = 0
continue
# s = get_inverse(1 + self.sk, self.n) * (k - r * self.sk) % self.n
s = self.d_1 * (k - r * self.sk) % self.n
if s == 0:
k = 0
else:
break
if outbytes:
return to_byte((r, s), self.keysize)
else:
return r, s
# 数字签名验证
# SM2第2部分 7.1
# 输入:收到的消息M′及其数字签名(r′, s′)、签名者的身份标识IDA及公钥PA、对M是否hash(默认是)
# 输出:True or False
def verify(self, M, sig, IDA, PA, dohash=True):
if isinstance(sig, bytes):
r = to_int(sig[:self.keysize])
s = to_int(sig[self.keysize:])
else:
r, s = sig
if not 1 <= r <= self.n - 1:
return False
if not 1 <= s <= self.n - 1:
return False
if dohash:
M_ = join_bytes([self.get_Z(IDA, PA), M])
e = to_int(sm3(M_))
else:
e = to_int(to_byte(M))
t = (r + s) % self.n
if t == 0:
return False
sG = self.Jacb_multiply(s, self.G, False)
tPA = self.Jacb_multiply(t, PA, False)
x1, y1 = self.Jacb_to_affine(self.Jacb_add(sG, tPA))
R = (e + x1) % self.n
if R == r:
return True
else: # 避免Jacobian坐标下的等价点导致判断失败
x1, y1 = self.add(self.Jacb_to_affine(sG), self.Jacb_to_affine(tPA))
R = (e + x1) % self.n
return R == r
# A 发起协商
# SM2第3部分 6.1 A1-A3
# 返回rA、RA
def agreement_initiate(self):
return self.gen_keypair()
# B 响应协商(option=True时计算选项部分)
# SM2第3部分 6.1 B1-B9
def agreement_response(self, RA, PA, IDA, option=False, rB=None, RB=None, klen=None):
# 参数准备
if not self.on_curve(RA):
return False, 'RA不在椭圆曲线上'
x1, y1 = RA
w = math.ceil(math.ceil(math.log(self.n, 2)) / 2) - 1
if not hasattr(self, 'sk'):
self.confirm_keypair()
h = 1 # SM2推荐曲线的余因子h=1
ZA = self.get_Z(IDA, PA)
ZB = self.get_Z()
# B1-B7
if not rB:
rB, RB = self.gen_keypair()
x2, y2 = RB
x_2 = (1 << w) + (x2 & (1 << w) - 1)
tB = (self.sk + x_2 * rB) % self.n
x_1 = (1 << w) + (x1 & (1 << w) - 1)
# V = self.multiply(h * tB, self.add(PA, self.multiply(x_1, RA)))
V = self.Jacb_multiply(h * tB, self.Jacb_add(self.Jacb_multiply(x_1, RA, False), PA))
if self.is_zero(V):
return False, 'V是无穷远点'
xV, yV = V
if not klen:
klen = KEY_LEN
KB = KDF(join_bytes([xV, yV, ZA, ZB]), klen)
if not option:
return True, (RB, KB)
# B8、B10(可选部分)
tmp = join_bytes([yV, sm3(join_bytes([xV, ZA, ZB, x1, y1, x2, y2]))])
SB = sm3(join_bytes([2, tmp]))
S2 = sm3(join_bytes([3, tmp]))
return True, (RB, KB, SB, S2)
# A 协商确认
# SM2第3部分 6.1 A4-A10
def agreement_confirm(self, rA, RA, RB, PB, IDB, SB=None, option=False, klen=None):
# 参数准备
if not self.on_curve(RB):
return False, 'RB不在椭圆曲线上'
x1, y1, x2, y2 = *RA, *RB
w = math.ceil(math.ceil(math.log(self.n, 2)) / 2) - 1
if not hasattr(self, 'sk'):
self.confirm_keypair()
h = 1 # SM2推荐曲线的余因子h=1
ZA = self.get_Z()
ZB = self.get_Z(IDB, PB)
# A4-A8
x_1 = (1 << w) + (x1 & (1 << w) - 1)
tA = (self.sk + x_1 * rA) % self.n
x_2 = (1 << w) + (x2 & (1 << w) - 1)
# U = self.multiply(h * tA, self.add(PB, self.multiply(x_2, RB)))
U = self.Jacb_multiply(h * tA, self.Jacb_add(self.Jacb_multiply(x_2, RB, False), PB))
if self.is_zero(U):
return False, 'U是无穷远点'
xU, yU = U
if not klen:
klen = KEY_LEN
KA = KDF(join_bytes([xU, yU, ZA, ZB]), klen)
if not option or not SB:
return True, KA
# A9-A10(可选部分)
tmp = join_bytes([yU, sm3(join_bytes([xU, ZA, ZB, x1, y1, x2, y2]))])
S1 = sm3(join_bytes([2, tmp]))
if S1 != SB:
return False, 'S1 != SB'
SA = sm3(join_bytes([3, tmp]))
return True, (KA, SA)
# B 协商确认(可选部分)
# SM2第3部分 6.1 B10
def agreement_confirm2(self, S2, SA):
if S2 != SA:
return False, 'S2 != SA'
return True, ''
# 加密
# SM2第4部分 6.1
# 输入:待加密的消息M(bytes或str类型)、对方的公钥PB、随机数k(不填则自动生成)
# 输出(True, bytes类型密文)或(False, 错误信息)
def encrypt(self, M, PB, k=None):
if self.is_zero(self.multiply(self.h, PB)): # S
return False, 'S是无穷远点'
M = to_byte(M)
klen = get_bit_num(M)
while True:
if not k:
k = random.randint(1, self.n - 1)
# x2, y2 = self.multiply(k, PB)
x2, y2 = self.Jacb_multiply(k, PB)
t = to_int(KDF(join_bytes([x2, y2]), klen))
if t == 0: # 若t为全0比特串则继续循环
k = 0
else:
break
# C1 = to_byte(self.multiply(k, self.G), self.keysize) # (x1, y1)
C1 = to_byte(self.Jacb_multiply(k, self.G), self.keysize) # (x1, y1)
C2 = to_byte(to_int(M) ^ t, klen >> 3)
C3 = sm3(join_bytes([x2, M, y2]))
return True, join_bytes([C1, C2, C3])
# 解密
# SM2第4部分 7.1
# 输入:密文C(bytes类型)
# 输出(True, bytes类型明文)或(False, 错误信息)
def decrypt(self, C):
x1 = to_int(C[:self.keysize])
y1 = to_int(C[self.keysize:self.keysize << 1])
C1 = (x1, y1)
if not self.on_curve(C1):
return False, 'C1不满足椭圆曲线方程'
if self.is_zero(self.multiply(self.h, C1)): # S
return False, 'S是无穷远点'
# x2, y2 = self.multiply(self.sk, C1)
x2, y2 = self.Jacb_multiply(self.sk, C1)
klen = len(C) - (self.keysize << 1) - HASH_SIZE << 3
t = to_int(KDF(join_bytes([x2, y2]), klen))
if t == 0:
return False, 't为全0比特串'
C2 = C[self.keysize << 1:-HASH_SIZE]
M = to_byte(to_int(C2) ^ t, klen >> 3)
u = sm3(join_bytes([x2, M, y2]))
C3 = C[-HASH_SIZE:]
if u != C3:
return False, 'u != C3'
return True, M
# 最简单的ECDH正确性测试
def test_ECDH(verify=False):
time_1 = get_cpu_time()
sm2 = SM2(genkeypair=False)
# A、B双方生成公、私钥
dA, PA = sm2.gen_keypair()
dB, PB = sm2.gen_keypair()
# 验证ECC系统参数和公钥
if verify:
if not sm2.para_valid():
print('椭圆曲线系统参数未通过验证:%s' % sm2.error)
return
if not sm2.pk_valid(PA):
print('PA未通过验证:%s' % sm2.error)
return
if not sm2.pk_valid(PB):
print('PB未通过验证:%s' % sm2.error)
return
# A将PA传给B,B将PB传给A
# A、B双方计算密钥
QA = sm2.Jacb_multiply(dA, PB)
KA = KDF(to_byte(QA), KEY_LEN)
QB = sm2.Jacb_multiply(dB, PA)
KB = KDF(to_byte(QB), KEY_LEN)
time_2 = get_cpu_time()
print('ECDH密钥协商完毕,耗时%.2f ms' % ((time_2 - time_1) * 1000))
print('KA == KB?: %s, value: 0x%s, len: %d' % (KA == KB, KA.hex(), len(KA) << 3))
# SM2密钥协商测试
def test_SM2_agreement(option=False):
time_1 = get_cpu_time()
# A、B双方初始化
sm2_A = SM2(ID='Alice')
sm2_B = SM2(ID='Bob')
# A、B均掌握对方的公钥和ID
PA, IDA = sm2_A.pk, sm2_A.ID
PB, IDB = sm2_B.pk, sm2_B.ID
# A 发起协商
rA, RA = sm2_A.agreement_initiate()
# A将RA发送给B
# B 响应协商
res, content = sm2_B.agreement_response(RA, PA, IDA, option)
if not res:
print('B报告协商错误:', content)
return
if option:
RB, KB, SB, S2 = content
else:
RB, KB = content
SB = None
# B将RB、(选项SB)发送给A
# A 协商确认
res, content = sm2_A.agreement_confirm(rA, RA, RB, PB, IDB, SB, option)
if not res:
print('A报告协商错误:', content)
return
if option:
KA, SA = content
else:
KA = content
if option:
# A将(选项SA)发送给B
# B 协商确认
res, content = sm2_B.agreement_confirm2(S2, SA)
if not res:
print('B报告协商错误:', content)
return
time_2 = get_cpu_time()
print('SM2密钥协商完毕,耗时%.2f ms' % ((time_2 - time_1) * 1000))
print('KA == KB?: %s, value: 0x%s, len: %d' % (KA == KB, KA.hex(), len(KA) << 3))
# SM2示例中的椭圆曲线系统参数
def demo_para():
p = 0x8542D69E4C044F18E8B92435BF6FF7DE457283915C45517D722EDB8B08F1DFC3
a = 0x787968B4FA32C3FD2417842E73BBFEFF2F3C848B6831D7E0EC65228B3937E498
b = 0x63E4C6D3B23B0C849CF84241484BFE48F61D59A5B16BA06E6E12D1DA27C5249A
xG = 0x421DEBD61B62EAB6746434EBC3CC315E32220B3BADD50BDC4C4E6C147FEDD43D
yG = 0x0680512BCBB42C07D47349D2153B70C4E5D7FDFCBFA36EA1A85841B9E46E09A2
n = 0x8542D69E4C044F18E8B92435BF6FF7DD297720630485628D5AE74EE7C32E79B7
G = (xG, yG)
h = 1
return p, a, b, n, G, h
# SM2数字签名与验证测试
# SM2第2部分 A.1 A.2
def test_signature():
IDA = '[email protected]'
M = 'message digest'
dA = 0x128B2FA8BD433C6C068C8D803DFF79792A519A55171B1B650C23661D15897263
xA = 0x0AE4C7798AA0F119471BEE11825BE46202BB79E2A5844495E97C04FF4DF2548A
yA = 0x7C0240F88F1CD4E16352A73C17B7F16F07353E53A176D684A9FE0C6BB798E857
PA = (xA, yA)
k = 0x6CB28D99385C175C94F94E934817663FC176D925DD72B727260DBAAE1FB2F96F
# A、B双方初始化
sm2_A = SM2(*demo_para(), IDA, dA, PA)
sm2_B = SM2(*demo_para())
time_1 = get_cpu_time()
# A对消息M进行签名
sig = sm2_A.sign(M, k)
# A将消息M签名(r, s)发送给B
# B对消息M签名进行验证
res = sm2_B.verify(M, sig, IDA, PA)
time_2 = get_cpu_time()
print('SM2签名、验证完毕,耗时%.2f ms' % ((time_2 - time_1) * 1000))
print('结果:%s,R值:%s' % (res, sig[:sm2_A.keysize].hex()))
# 验证通过,输出的r值(40f1ec59f793d9f49e09dcef49130d4194f79fb1eed2caa55bacdb49c4e755d1)与SM2第2部分 A.2中的结果一致
# SM2密钥协商测试2
# SM2第3部分 A.1 A.2
def test_SM2_agreement2(option=False):
IDA = '[email protected]'
IDB = '[email protected]'
dA = 0x6FCBA2EF9AE0AB902BC3BDE3FF915D44BA4CC78F88E2F8E7F8996D3B8CCEEDEE
xA = 0x3099093BF3C137D8FCBBCDF4A2AE50F3B0F216C3122D79425FE03A45DBFE1655
yA = 0x3DF79E8DAC1CF0ECBAA2F2B49D51A4B387F2EFAF482339086A27A8E05BAED98B
PA = (xA, yA)
dB = 0x5E35D7D3F3C54DBAC72E61819E730B019A84208CA3A35E4C2E353DFCCB2A3B53
xB = 0x245493D446C38D8CC0F118374690E7DF633A8A4BFB3329B5ECE604B2B4F37F43
yB = 0x53C0869F4B9E17773DE68FEC45E14904E0DEA45BF6CECF9918C85EA047C60A4C
PB = (xB, yB)
rA = 0x83A2C9C8B96E5AF70BD480B472409A9A327257F1EBB73F5B073354B248668563
x1 = 0x6CB5633816F4DD560B1DEC458310CBCC6856C09505324A6D23150C408F162BF0
y1 = 0x0D6FCF62F1036C0A1B6DACCF57399223A65F7D7BF2D9637E5BBBEB857961BF1A
RA = (x1, y1)
rB = 0x33FE21940342161C55619C4A0C060293D543C80AF19748CE176D83477DE71C80
x2 = 0x1799B2A2C778295300D9A2325C686129B8F2B5337B3DCF4514E8BBC19D900EE5
y2 = 0x54C9288C82733EFDF7808AE7F27D0E732F7C73A7D9AC98B7D8740A91D0DB3CF4
RB = (x2, y2)
time_1 = get_cpu_time()
# A、B双方初始化
sm2_A = SM2(*demo_para(), IDA, dA, PA)
sm2_B = SM2(*demo_para(), IDB, dB, PB)
# A 发起协商
# A生成rA, RA,将RA发送给B
# B 响应协商
res, content = sm2_B.agreement_response(RA, PA, IDA, option, rB, RB)
if not res:
print('B报告协商错误:', content)
return
if option:
RB, KB, SB, S2 = content
else:
RB, KB = content
SB = None
# B将RB、(选项SB)发送给A
# A 协商确认
res, content = sm2_A.agreement_confirm(rA, RA, RB, PB, IDB, SB, option)
if not res:
print('A报告协商错误:', content)
return
if option:
KA, SA = content
else:
KA = content
if option:
# A将(选项SA)发送给B
# B 协商确认
res, content = sm2_B.agreement_confirm2(S2, SA)
if not res:
print('B报告协商错误:', content)
return
time_2 = get_cpu_time()
print('SM2密钥协商完毕,耗时%.2f ms' % ((time_2 - time_1) * 1000))
print('KA == KB?: %s, value: 0x%s, len: %d' % (KA == KB, KA.hex(), len(KA) << 3))
# 协商成功,输出的密钥(55b0ac62a6b927ba23703832c853ded4)与SM2第3部分 A.2中的结果一致
# SM2加解密测试
# SM2第4部分 A.1 A.2
def test_encryption():
M = 'encryption standard'
dB = 0x1649AB77A00637BD5E2EFE283FBF353534AA7F7CB89463F208DDBC2920BB0DA0
xB = 0x435B39CCA8F3B508C1488AFC67BE491A0F7BA07E581A0E4849A5CF70628A7E0A
yB = 0x75DDBA78F15FEECB4C7895E2C1CDF5FE01DEBB2CDBADF45399CCF77BBA076A42
PB = (xB, yB)
k = 0x4C62EEFD6ECFC2B95B92FD6C3D9575148AFA17425546D49018E5388D49DD7B4F
# A、B双方初始化
sm2_A = SM2(*demo_para())
sm2_B = SM2(*demo_para(), '', dB, PB)
time_1 = get_cpu_time()
# A用B的公钥对消息M进行加密
res, C = sm2_A.encrypt(M, PB, k)
if not res:
print('A报告加密错误:', C)
return
# A将密文C发送给B
# B用自己的私钥对密文C进行解密
res, M2 = sm2_B.decrypt(C)
if not res:
print('B报告解密错误:', M2)
return
time_2 = get_cpu_time()
print('SM2加解密完毕,耗时%.2f ms' % ((time_2 - time_1) * 1000))
print('结果:%s,解密得:%s(%s)' % (res, M2.hex(), M2.decode()))
# 加解密成功,解密后的16进制值(656e6372797074696f6e207374616e64617264)与SM2第4部分 A.2中的结果一致
if __name__ == "__main__":
test_ECDH()
test_SM2_agreement(True)
# 可复现SM2文档中的示例结果
test_signature()
test_SM2_agreement2(True)
test_encryption()
“他们要打多久,就打多久,一直打到完全胜利!”
多用SM2,少用RSA,不用DH;多用SM3,少用SHA,不用MD5;多用SM4,少用AES,不用DES。支持国密,支持自主,不光是情怀,而是国密算法确实设计得好,易用,安全性高!
目前,对于国密算法的python实现,在代码开源、算法优化、稳定性方面还不及国外的成熟库,幸而我们的国家一直不乏有识之士踔厉奋发、笃行不怠、负重前行。
望大家共同努力,把网络信息安全牢牢掌握在自己手中,共勉!
版权归原作者 qq_43339242 所有, 如有侵权,请联系我们删除。