0
0

机器学习——决策树的创建

一、什么是决策树？

1.决策树概念：** **

** 简单来说决策树就是一棵树，一颗决策树包含一个根节点、若干个内部结点和若干个叶结点，叶结点就是问题的决策结果。也就是说一棵树包括根节点、父节点、子节点、叶子节点。子节点由父节点分裂出来，然后子节点作为新的父节点继续分裂，直到得出最终结果。**

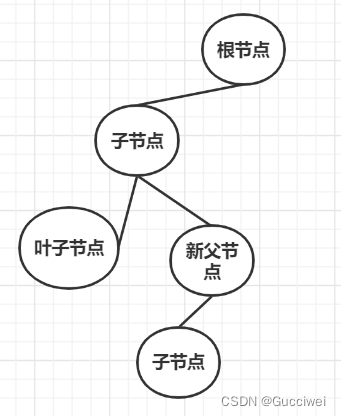
2.决策树实例：

       假设给了一个动物的名字它的一些特征，然后我们需要根据这些特征来判断这个动物是否属于哺乳动物。

动物名称体温呼吸胎生毛发哺乳动物猫恒温肺是是是蛇冷血腮否否否

         **决策树如下**：

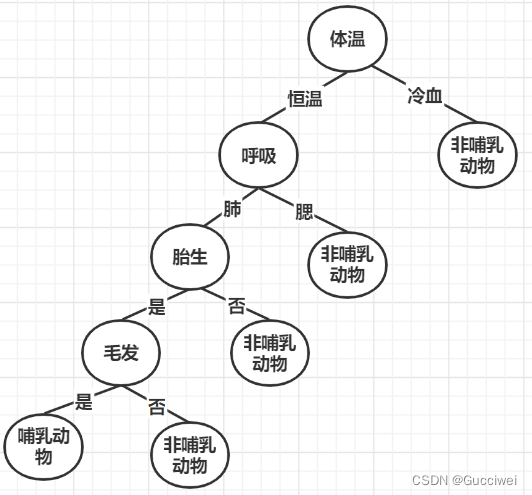
二、决策树构造的ID3算法

1.决策树的构造过程

动物名称食物体温呼吸方式胎生毛发生活环境哺乳动物老虎肉食恒温肺是是草原是蛇肉食冷血腮否否森林否鱼杂食冷血腮否否水里否羊草恒温肺是是草原是长颈鹿草恒温肺是是草原是熊猫杂食恒温肺是是森林是大像草恒温肺是否森林是青蛙肉冷血腮否否水里否乌龟肉冷血腮否否水里否蓝鲸肉恒温肺是否水里是

第一步：将所有的特征看成一个个节点。（特征：体温，呼吸方式，胎生，毛发等）

第二步：遍历当前特征的子节点，找到最适合的划分点。计算划分之后所有子节点的纯度信息。（比如：体温这个特征按照恒温和冷血来划分）

第三步：使用第二步遍历所有特征，选出该特征最优的划分方式，得出最终的子节点。

上述决策过程存在两个问题：

1.应该选择哪一个特征最适合划分？

2.什么时候停止划分？

2.使用ID3算法划分特征

    信息熵：熵(entropy)表示混乱程度，熵越大，越混乱。假设有一个集合D,其中有X个随机变量，其中第i个元素在集合中出现的概率为Pi。

H(D)=-\sum_{i=1}^{x} pi\log_{2}{pi}

  其中pi表示类i的数量占比。假设二分类问题A,B两类，如果A的数量等于B的数量，那么分类节点的纯度就会达到最低，熵等于1，只有当节点的信息都属于A类或者是B类时，熵=1。 

    信息增益：（ingormation gain）,表示已知A的特征信息，而使得B类信息的不确定性降低的程度。计算公式如下：

Gain(D,A)=H(D)-H(D|A) =H(D)-\sum_{v=1}^{V} \frac{|D^{v} |}{|D|} H(D^{v} )

  对于一个数据集，将所有的特征属性进行划分操作，之后将划分操作的结果集的纯度进行比较，选择纯度高的特征属性作为当前的划分节点。

三、实现决策树

1.建立数据集：每行数据代表一个样本，每个样本的前6个数据代表6个特征，第7个数据代表样本的分类。下面的标签表示每个样本的这6个特征分别是啥，创建的这六个样本分别是老虎，蛇，鱼，羊，熊猫和蓝鲸。

def createDataSet():
    dataSet = [[0,0,0,0,0,0,'是'],
               [1,1,1,1,0,1,'否'],
               [1,1,1,1,1,2,'否'],
               [0,0,0,0,2,0,'是'],
               [0,0,0,1,2,1,'是'],
               [0,0,0,1,0,2,'是']]
    #（0恒温，1冷血），（0肺，1腮），（0胎生，1非胎生），（0有毛发，1无毛发）
    #(0肉食，1杂食，2草)，（0草原，1森林，2水里）
    labels = ['体温','呼吸方式','胎生','毛发','食物','生活环境']
    return dataSet, labels

2.根据公式计算信息熵：featVec[-1]表示每个样本中的数据的最后一个数据的值，也就是“是”和“否”两个类别。

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)  #数据集样本数
    labelCounts = {}  #构建字典保存每个标签出现的次数
    for featVec in dataSet:
        #给每个分类(这里是[是,否])创建字典并统计各种分类出现的次数
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:   #计算信息熵
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * math.log(prob,2)   #信息增益计算熵
    return shannonEnt

3.按类别划分数据集：

def splitDataSet(dataSet,axis,value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:  #开始遍历数据集
            #featVec 是一维数组，下标为axis元素之前的值加入到reducedFeatVec
            reducedFeatVec = featVec[:axis]
            #下一行的内容axis+1之后的元素加入到reducedFeatVec
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    #返回划分好后的数据集
    return retDataSet

4.选择最后的数据特征作为划分标准：dataSet[0]代表第一个样本，[0,0,0,0,0,0,'是']，长度为7, 7-1=6，6表示该样本的特征数。

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0   #信息增益
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)  #值去重
        newEntropy = 0.0   #信息熵
        for value in uniqueVals: #计算信息增益
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        print("第%d个特征的信息增益为%.1f"%(i,infoGain))
        if (infoGain > bestInfoGain):  #选出最大的信息增益
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

5.存储：用 字典储存统计出的每个属性)的各个值出现的次数

def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
        sortedClassCount = sorted(classCount.iteritems(),  key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

6.最后一步，创建树：

def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]   #当所有类型都相同时 返回这个类型
    if len(dataSet[0]) == 1:  #当没有可以在分类的特征集时
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])  #已经选择的特征不在参与分类
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        #对每个特征集递归调用建树方法
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree

7.结果:存在问题，当计算信息增益保留1位和保留4位小数时，前3个特征的信息增益无法比较，也就是说可以直接根据这个动物的体温直接判断这个动物是哺乳动物还是非哺乳动物，或者是胎生和毛发也可以确定这个动物是否是哺乳动物。出现这个情况的原因应该是数据样本数量较少，还有ID3这个算法的原因。

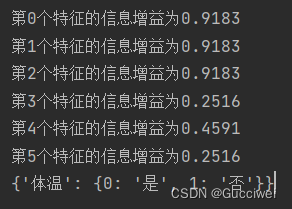
8.完整代码：

import math
import operator
import numpy as np
from numpy import tile

def createDataSet():
    dataSet = [[0,0,0,0,0,0,'是'],
               [1,1,1,1,0,1,'否'],
               [1,1,1,1,1,2,'否'],
               [0,0,0,0,2,0,'是'],
               [0,0,0,1,2,1,'是'],
               [0,0,0,1,0,2,'是']]
    #（0恒温，1冷血），（0肺，1腮），（0胎生，1非胎生），（0有毛发，1无毛发）
    #(0肉食，1杂食，2草)，（0草原，1森林，2水里）
    labels = ['体温','呼吸方式','胎生','毛发','食物','生活环境']
    return dataSet, labels

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)  #数据集样本数
    labelCounts = {}  #构建字典保存每个标签出现的次数
    for featVec in dataSet:
        #给每个分类(这里是[是,否])创建字典并统计各种分类出现的次数
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:   #计算信息熵
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * math.log(prob,2)   #信息增益计算熵
    return shannonEnt

def splitDataSet(dataSet,axis,value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:  #开始遍历数据集
            #featVec 是一维数组，下标为axis元素之前的值加入到reducedFeatVec
            reducedFeatVec = featVec[:axis]
            #下一行的内容axis+1之后的元素加入到reducedFeatVec
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    #返回划分好后的数据集
    return retDataSet

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0   #信息增益
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)  #值去重
        newEntropy = 0.0   #信息熵
        for value in uniqueVals: #计算信息增益
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        print("第%d个特征的信息增益为%.4f"%(i,infoGain))
        if (infoGain > bestInfoGain):  #选出最大的信息增益
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
        sortedClassCount = sorted(classCount.iteritems(),  key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]   #当所有类型都相同时 返回这个类型
    if len(dataSet[0]) == 1:  #当没有可以在分类的特征集时
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])  #已经选择的特征不在参与分类
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        #对每个特征集递归调用建树方法
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
    return myTree

if __name__ == '__main__':

    myDat,labels = createDataSet()
    print(createTree(myDat, labels))

四、总结

1.决策树

优点：易于理解和解释，决策树分类很快，可以处理不相关特征数据。

缺点： 对缺失数据的数据集处理困难。它构建过程是一个递归的过程，需要确定停止条件，否则过程将不会结束。很容易出现过拟合问题。

2.ID3算法

ID3只适合在小规模数据集上使用。

3.此次实验暂时无法将决策树可视化

原因：plt.的安装包出现问题。

标签： 决策树 人工智能
本文转载自: https://blog.csdn.net/Gucciwei/article/details/127867733
版权归原作者 Gucciwei 所有， 如有侵权，请联系我们删除。
登录后发布评论

“机器学习——决策树的创建”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

机器人技术在安全领域的重要作用

安全学习记录——网络篇（一）

图腾柱PFC：HP1010为您的电动两轮车之旅提供绿色，高效，安全的动力

单元测试数据库回滚问题

这才是单元测试，之前我们都错了

【C语言基础】：字符函数和字符串函数

ChatGPT-Next-Web SSRF漏洞+XSS漏洞复现(CVE-2023-49785)

文章导航