Pytorch学习笔记（5）：torch.nn---网络层介绍（卷积层、池化层、线性层、激活函数层）

前期回顾：

Pytorch学习笔记（1）：基本概念、安装、张量操作、逻辑回归

Pytorch学习笔记（2）：数据读取机制（DataLoader与Dataset）

Pytorch学习笔记（3）：图像的预处理（transforms）

Pytorch学习笔记（4）：模型创建（Module）、模型容器（Containers）、AlexNet构建

一、卷积层—Convolution Layers

卷积运算：卷积核在输入信号（图像）上滑动，相应位置上进行乘加。

卷积核：又称滤波器，过滤器，可认为是某种模式，某种特征。

卷积过程：类似于用一个模板去图像上寻找与它相似的区域，与卷积核模式越相似，激活值越高，从而实现特征提取。

1.1 1d / 2d / 3d卷积

卷积维度：一般情况下，卷积核在几个维度上滑动，就是几维卷积

（1）1d卷积示意

（2）2d卷积示意

（3）3d卷积示意

1.2 卷积—nn.Conv2d()

nn.Conv2d

功能：对多个二维信号进行二维卷积

主要参数：

• in_channels：输入通道数
• out_channels：输出通道数，等价于卷积核个数
• kernel_size：卷积核尺寸
• stride：步长
• padding：填充个数（一般用来保持输入输出尺寸一致）
• dilation：空洞卷积大小
• groups：分组卷积设置
• bias：偏置

尺寸计算方式：

Conv2d运算原理：

主要代码段如下：

（1）加载图片，将图片处理成张量的形式：

# ================================= load img ==================================

path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "pig.jpeg")
print(path_img)
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
# 添加 batch 维度
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

（2） 进行卷积操作：

# =============== create convolution layer ==================

# ================ 2d
 flag = 1
#flag = 0
if flag:
    #定义一个卷积层
    conv_layer = nn.Conv2d(3, 1, 3)   # input:(i, o, size) weights:(o, i , h, w)
    # 初始化卷积层权值
    nn.init.xavier_normal_(conv_layer.weight.data)
    # nn.init.xavier_uniform_(conv_layer.weight.data)

    # 卷积运算
    img_conv = conv_layer(img_tensor)

（3）运行并打印图片：

# ================================= visualization ==================================
print("卷积前尺寸:{}\n卷积后尺寸:{}".format(img_tensor.shape, img_conv.shape))
img_conv = transform_invert(img_conv[0, 0:1, ...], img_transform)
img_raw = transform_invert(img_tensor.squeeze(), img_transform)
plt.subplot(122).imshow(img_conv, cmap='gray')
plt.subplot(121).imshow(img_raw)
plt.show()

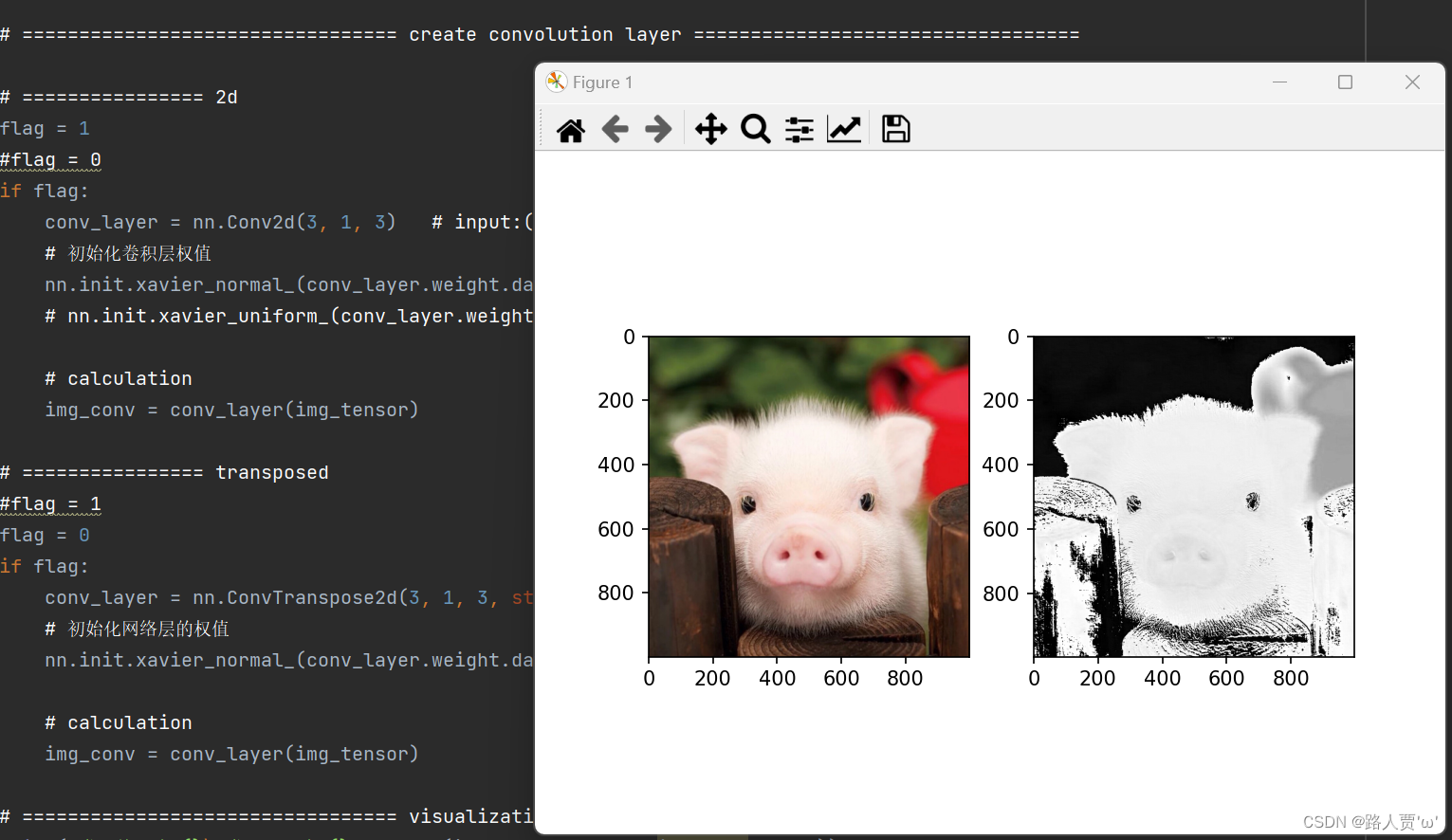
我们来看一下效果，可以看到，卷积核对特征进行了提取：

我们再看一下图像尺寸的变化：

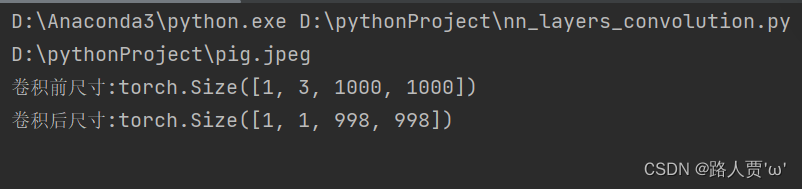
卷积前，图像尺寸是1000×1000, 卷积后， 图像尺寸是998×998。我们这里的卷积核设置， 输入通道3， 卷积核个数1， 卷积核大小3， 无padding，步长是1， 那么我们根据上面的公式， 输出尺寸:(1000−3)/1+1=998

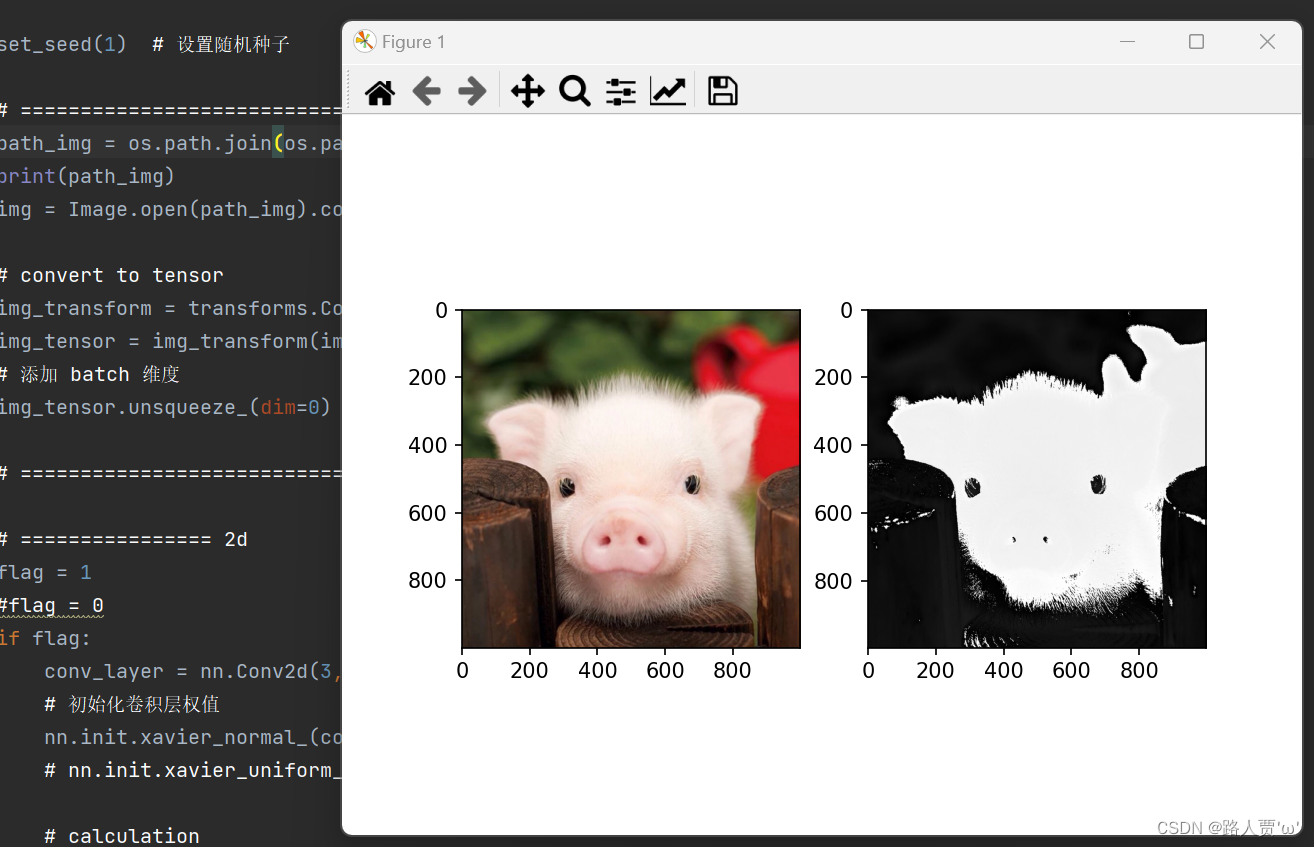
我们继续随机初始化卷积核权重进行卷积后，则会出现以下效果：

1.3 转置卷积—nn.ConvTranspose

nn.ConvTranspose2d

功能：转置卷积实现上采样

主要参数：

• in_channels：输入通道数
• out_channels：输出通道数
• kernel_size：卷积核尺寸
• stride：步长
• padding：填充个数
• dilation：空洞卷积大小
• groups：分组卷积设置
• bias：偏置

**转置卷积的尺寸计算（卷积运算的尺寸逆）： **

转置卷积代码如下：

# ================ transposed
flag = 1
# flag = 0
if flag:
    conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2)   # input:(input_channel, output_channel, size)
    # 初始化网络层的权值
    nn.init.xavier_normal_(conv_layer.weight.data)

    # calculation
    img_conv = conv_layer(img_tensor)

**转置卷积结果： **

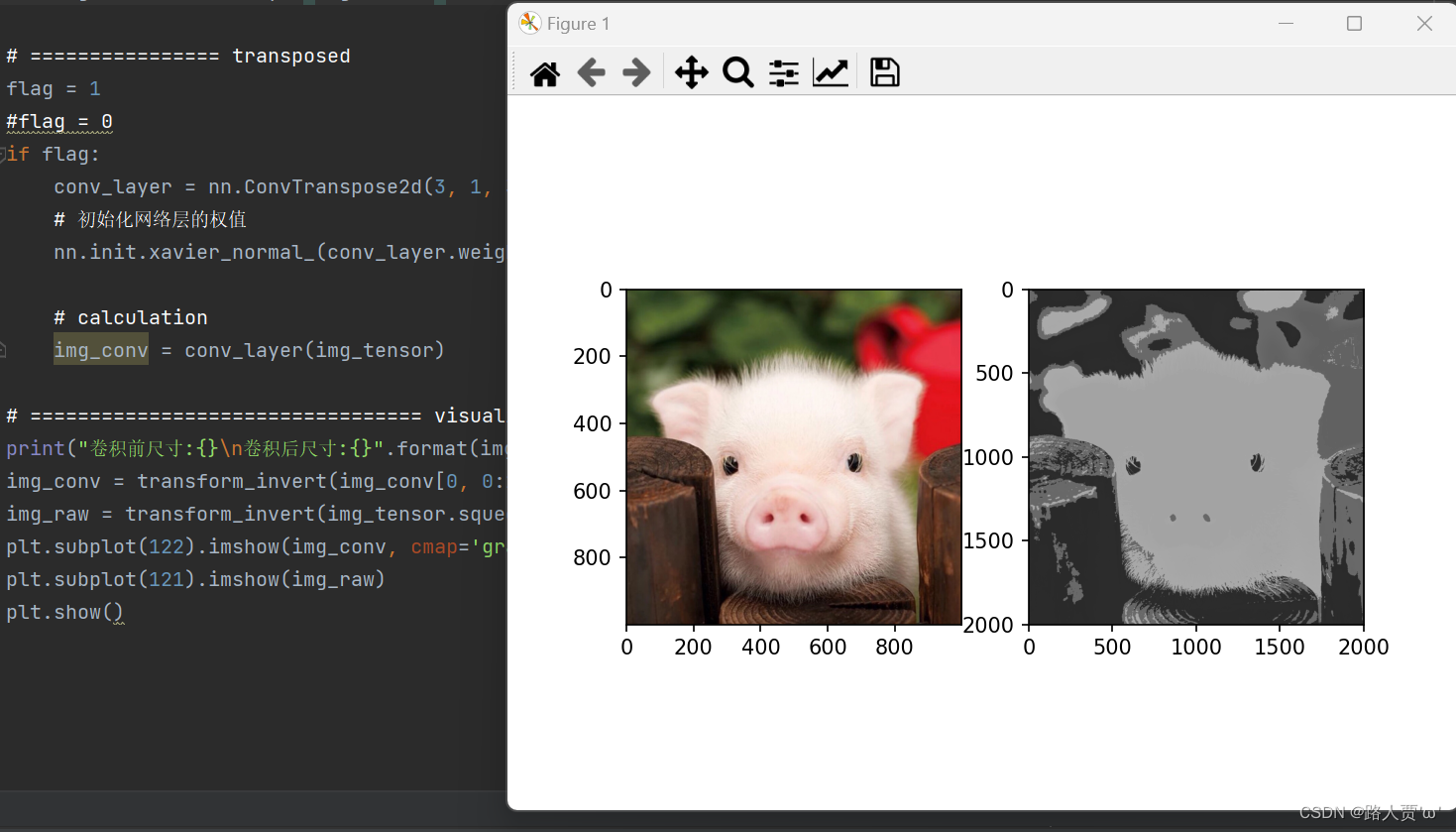
我们再看一下图像尺寸的变化：

我们发现，输入图像是1000的， 卷积核大小是3，stride=2， 所以输出尺寸：(1000−1)×2+3=2001

二、池化层—Pooling Layer

** 池化运算：**对信号进行“收集”并“总结”， 类似水池收集水资源， 因而叫作池化层。

“收集”：多变少

“总结”：最大值 or 平均值

如图用2×2的窗口进行池化操作，最大池化用最大值代替这个窗口，平均池化用平均值代替这个窗口。

（1）nn.MaxPool2d

功能：对二维信号（图像）进行最大值池化

主要参数：

• kernel_size：卷积核尺寸
• stride：步长
• padding：填充个数
• dilation：池化间隔大小
• ceil_mode：尺寸向上取整,默认为False
• return_indices：记录池化像素索引

*注意：*stride一般设置的与窗口大小一致，以避免重叠

具体代码如下：

数据预处理：

set_seed(1)  # 设置随机种子

# ================================= load img ==================================
path_img = os.path.join(os.path.dirname(os.path.abspath(__file__)), "pig.jpeg")
img = Image.open(path_img).convert('RGB')  # 0~255

# convert to tensor
img_transform = transforms.Compose([transforms.ToTensor()])
img_tensor = img_transform(img)
img_tensor.unsqueeze_(dim=0)    # C*H*W to B*C*H*W

最大池化代码：

# ================ maxpool
 flag = 1
#flag = 0
if flag:
    maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2))   # input:(i, o, size) weights:(o, i , h, w)
    img_pool = maxpool_layer(img_tensor)

我们来看一下最大池化的效果：

输出尺寸变化：

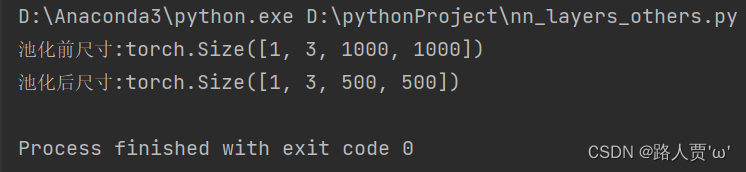
我们可以发现，图像基本上没什么差别，但是图像的尺寸减少了一半， 所以池化层是可以帮助我们剔除一些冗余像素或减少后面计算量。

（2）nn.AvgPool2d

功能：对二维信号（图像）进行平均值池化

主要参数：

• kernel_size：卷积核尺寸
• stride：步长
• padding：填充个数
• dilation：池化间隔大小
• count_include_pad ：填充值用于计算
• divisor_override：除法因子（自定义分母）

平均池化代码：

# ================ avgpool
flag = 1
#flag = 0
if flag:
    avgpoollayer = nn.AvgPool2d((2, 2), stride=(2, 2))   # input:(i, o, size) weights:(o, i , h, w)
    img_pool = avgpoollayer(img_tensor)

我们来看一下平均池化的效果：

输出尺寸变化：

最大值池化和平均池化的差别：最大池化的亮度会稍微亮一些，毕竟它都是取的最大值，而平均池化是取平均值。

（3）nn.MaxUnpool2d

功能：对二维信号（图像）进行最大值池化上采样（反池化：将大尺寸图像变为小尺寸图像）

主要参数：

• kernel_size：卷积核尺寸
• stride：步长
• padding：填充个数

这里的参数与池化层是类似的。唯一的不同就是前向传播的时候我们需要传进一个indices， 我们的索引值，要不然不知道把输入的元素放在输出的哪个位置上。

反池化代码：

# ================ max unpool
flag = 1
#flag = 0
if flag:
    # pooling
    img_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)
    #最大值池化保留索引    
    maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)
    img_pool, indices = maxpool_layer(img_tensor)

    # unpooling
    img_reconstruct = torch.randn_like(img_pool, dtype=torch.float)
    #反池化操作
    maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))
    img_unpool = maxunpool_layer(img_reconstruct, indices)

    print("raw_img:\n{}\nimg_pool:\n{}".format(img_tensor, img_pool))
    print("img_reconstruct:\n{}\nimg_unpool:\n{}".format(img_reconstruct, img_unpool))

输出结果：

三、线性层—Linear Layer

线性层又称为全连接层，其每个神经元与上一层所有神经元相连实现对前一层的线性组合，线性变换。

** nn.Linear**

功能：对一维信号（向量）进行线性组合

主要参数：

• in_features：输入结点数
• out_features：输出结点数
• bias：是否需要偏置

计算公式：y = 𝒙𝑾𝑻 + 𝒃𝒊𝒂𝒔

**具体代码如下： **

# ================ linear
flag = 1
# flag = 0
if flag:
    inputs = torch.tensor([[1., 2, 3]])
    linear_layer = nn.Linear(3, 4)
    linear_layer.weight.data = torch.tensor([[1., 1., 1.],
                                             [2., 2., 2.],
                                             [3., 3., 3.],
                                             [4., 4., 4.]])

    #设置偏置
    linear_layer.bias.data.fill_(0)
    output = linear_layer(inputs)
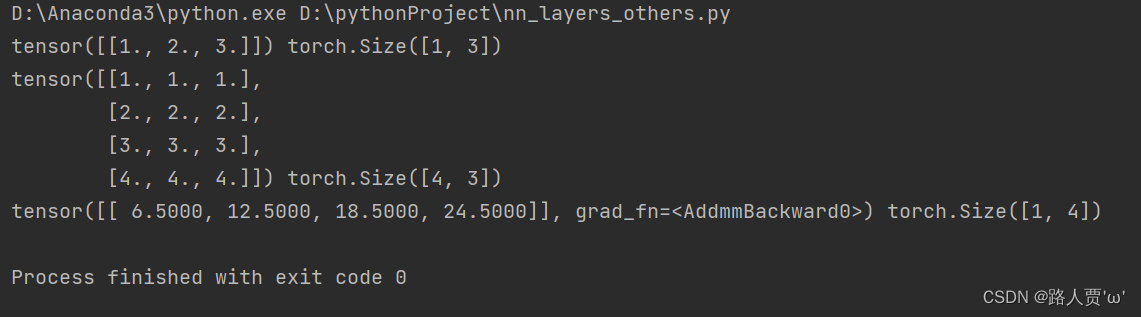
    print(inputs, inputs.shape)
    print(linear_layer.weight.data, linear_layer.weight.data.shape)
    print(output, output.shape)

** 运行结果：**

偏置为0：

偏置为0.5：

四、激活函数层—Activate Layer

激活函数对特征进行非线性变换，赋予多层神经网络具有深度的意义

（1）nn.Sigmoid

代码：

m = nn.Sigmoid()
input = torch.randn(2)
output = m(input)

（2）nn.tanh

代码：

m = nn.Tanh()
input = torch.randn(2)
output = m(input)

（3）nn.ReLU

代码：

  >>> m = nn.ReLU()
  >>> input = torch.randn(2)
  >>> output = m(input)

（4）nn.LeakyReLU

• negative_slope：负半轴斜率

** 代码：**

m = nn.LeakyReLU(0.1)
input = torch.randn(2)
output = m(input)

（5）nn.PReLU

• init：可学习斜率

**代码： **

m = nn.PReLU(3)
output = m(input)
print(output)

（6）nn.RReLU

• lower：均匀分布下限
• upper：均匀分布上限

** 代码：**

>>> m = nn.RReLU(0.1, 0.3)
>>> input = torch.randn(2)
>>> output = m(input)

本文参考：

系统学习Pytorch笔记五：nn的网络层介绍(卷积层，池化层，激活函数，全连接层等)

[PyTorch 学习笔记] 3.3 池化层、线性层和激活函数层 - 知乎 (zhihu.com)