还记得LeCun被拒的论文VICReg吗,今天我们就来说说它
在深度网络中权重和激活那个更重要?显然是权重,因为我们可以从权重推导出网络的激活。但是深度网络是非线性嵌入函数;我们只想要这种非线性嵌入。在这种嵌入基础上进行训练并获得结果(例如分类),我们要么需要在分类网络中使用线性分类器,要么需要在输出的特征中计算相似度。但是与权重衰减正则化相比,特征嵌入正则化在论文中却很少被提到和使用。通过权重衰减的正则化可以明显影响网络的性能,尤其是在小数据集上[3]。同样,特征嵌入也可以带来重大影响,例如避免模式崩溃(model collapse)。在本文中,我将介绍两个相关的特征嵌入正则化器:SVMax [1] 和 VICReg [2]。
SVMax 和 VICReg 都是无监督的正则化器,它们都支持监督学习和非/自监督学习,在训练期间可以处理单独的小批量,所以不需要对数据集进行其他的预处理。为了统一起见本篇文章将使用相同的符号来描述两者:我们有一个网络 N,它接受一个大小为 b 的 mini-batch输入 并生成一个 d 维嵌入,即我们有一个输出特征嵌入矩阵 E ∈ R^{b × d},如图 1 所示。矩阵 E 可以从任何网络层中提取,但它通常是从网络的倒数第二层中提取的,即在全局平均池化层之后。
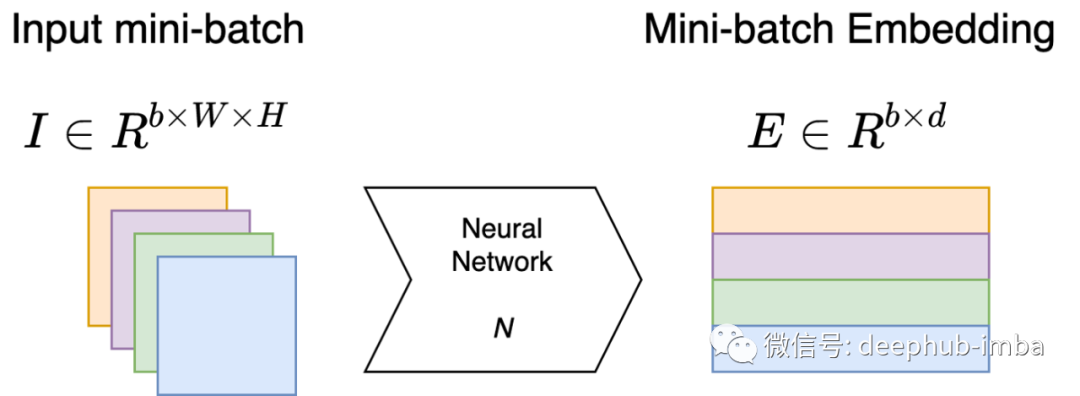
图1:网络N在训练过程中,对于规模为b的小批量,生成特征嵌入矩阵E∈R^{b × d}。
SVMax 和 VICReg 都显式地对单层的特征嵌入输出进行了正则化,这样也就隐式地对网络的权重进行了正则化。对于 d 维特征嵌入,SVMax 和 VICReg 都旨在激活所有维度。换句话说,两个正则化器的目标是让每个神经元(维度)同样有可能触发。这样可以使某些维度(神经元)始终处于活动/非活动状态而与输入无关,也就避免了模式崩溃(model collapse)。
模式崩溃(model collapse):也称为 Helvetica scenario是GAN中提出的感念。当生成器学习将几个不同的输入 z 值映射到同一输出点时发生的问题。实际上完全模式崩溃很少见,但部分模式崩溃很常见。部分模式崩溃是指生成器制作包含相同颜色或纹理主题的多张图像,或包含同一物体的不同视图的多张图像的场景。
简单形象地来讲,模式崩溃就是团队中的人员对的目标的理解不同,所以整个团队虽然都在努力的工作,但是都是按照自己理解的目标前进,没有统一的领导所以整个团队都乱成一团了!
SVMax
SVMax [1] 被提出用于度量学习(Metric Learning)也就是常说的相似度学习,其中特征嵌入在单位圆上进行归一化,即 l2 归一化。因此,SVMax 旨在将特征嵌入均匀地分散在单位圆上,如图 2(右)所示。在该图中矩形矩阵 E 的奇异值之间存在显着差异。当特征在单个或几个维度上极化时,如图 2(左)所示,单个或几个奇异值较大 而其余的小。相反当特征均匀分散时,所有维度都变得活跃并且所有奇异值都增加,即平均奇异值增加。
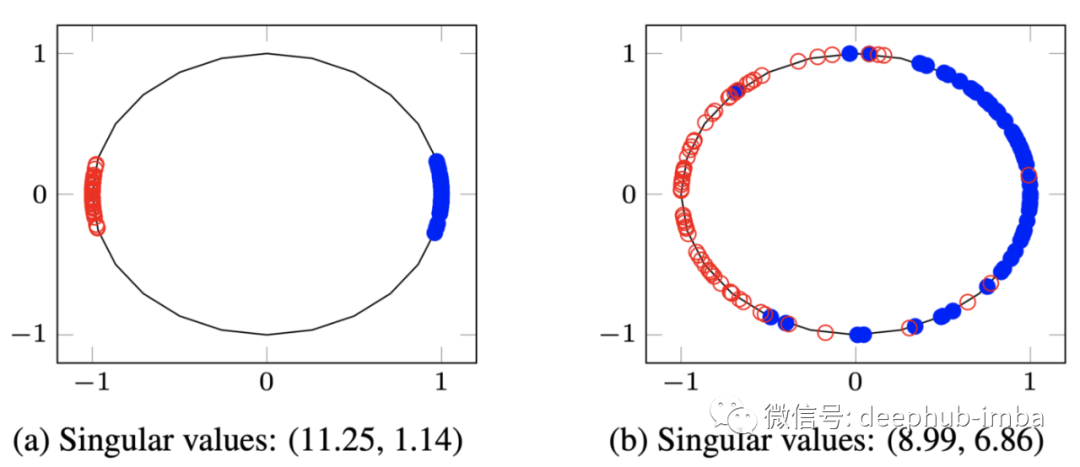
图 2:分散在 2D 单位圆上的特征嵌入。在(a)中,特征在单个轴上极化;主轴(横)轴奇异值大,副(纵)轴奇异值小。在(b)中,特征在两个维度上均匀分布;两个奇异值都比较大。
SVMax 利用这一观察结果并正则化 E 以最大化其平均奇异值。SVMax 的最简单形式如下
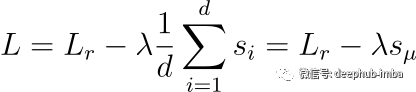
图 3:原始的 SVMax 公式。L_r 是使用 SVMax 正则化器之前的原始损失函数,而 s_μ 是要最大化的平均奇异值。
其中 s_μ 是要最大化的平均奇异值,L_r 是原始损失函数(例如,交叉熵)。
SVMax 进一步利用单位圆(l2 归一化)约束来建立平均奇异值 s_μ 的刚性下限和上限。例如当矩阵 E 的秩为 1,即 Rank(E)=1 时,s_μ 的下限成立。这是模式崩溃的一个明显案例,其中单个维度始终处于活动状态。在这种情况下,s_μ 的下限等于
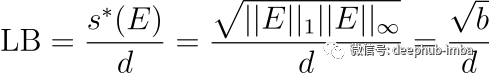
图 4:当除第一个(最大的)奇异值之外的所有奇异值都为零时,平均奇异值的下限成立。s*(E)是当所有其他奇异值都为零时最大奇异值的值。
其中 ||E||_1 和 ||E||_∞ 分别是 L-1 范数和 L-Infinity 范数。类似地,SVMax 在 s_μ 上建立一个上限如下
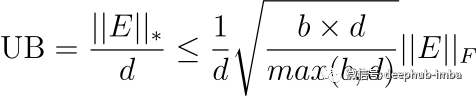
图 5:使用核范数 ||E||_* 和 Frobenius 范数 ||E||_F 建立的平均奇异值的上限。
这些界限带来两个好处:(1)很容易调整 SVMax 的平衡超参数 λ(图 3),因为在训练开始之前就知道 s_μ 的范围;(2) 平均奇异值及其边界作为量化指标来评估训练后的网络——包括非正则化网络。例如,图 6 评估了用不同批量大小训练的四个网络。对于每个网络,平均奇异值是在分割后的测试数据上计算的,即训练后评估。与非正则化网络相比,使用 SVMax 训练的网络显着更好地利用了特征嵌入。
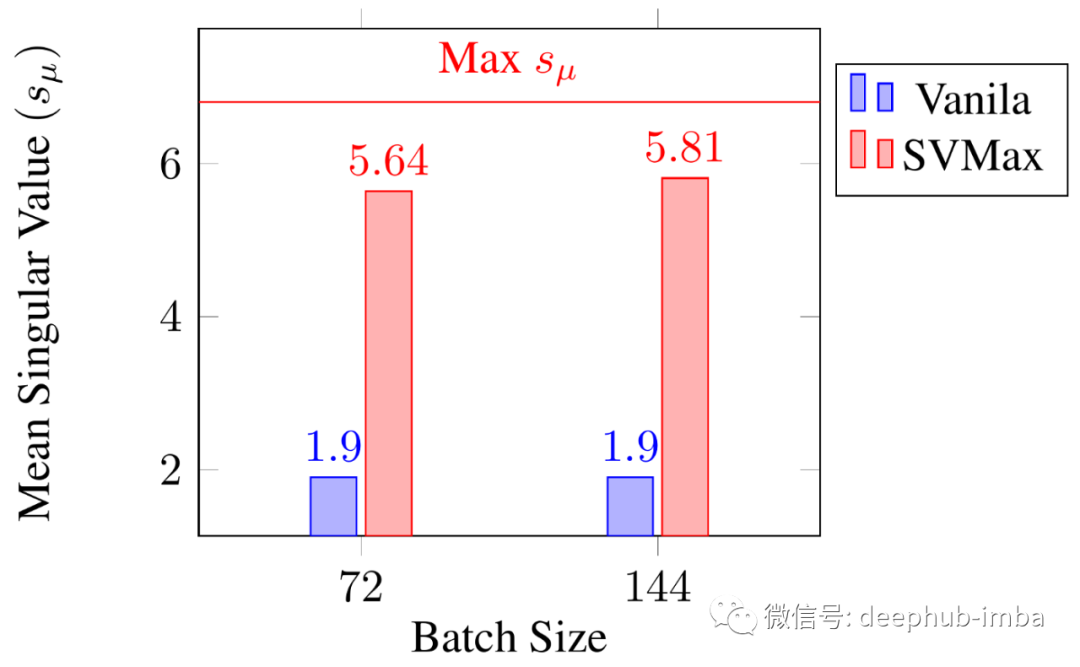
图 6:四种不同特征嵌入(度量学习)网络的平均奇异值。X 和 Y 轴表示小批量大小 b 和 CUB-200 测试拆分的特征嵌入的 s_μ。特征嵌入是使用对比损失进行训练的,包含了有和没有 SVMax的结果。水平红线表示 s_μ 的上限。
尽管SVMax很简单,并且有严格的数学界限,但它的计算成本很高。平均奇异值的计算复杂度随着矩阵维数的增加而增加。这就是下一个方法VICReg的改进之处,它提供了一种更轻量的计算方式并且也很有效果。
VICReg
VICReg [2] 就是LeCun大神被拒的论文了😄,如果特征嵌入不进行归一化时,也可以用于自监督学习。VICReg 有三个概念,但本文将只关注一个概念——方差。该概念旨在激活特征嵌入矩阵 E 中的每个维度。VICReg 计算小批量 E 的标准偏差 (std),如图 7 所示。这会生成一个具有 d 维度的向量,每个维度 表示单个维度的激活。标准差为零的维度是崩溃维度——维度始终处于打开/关闭状态。
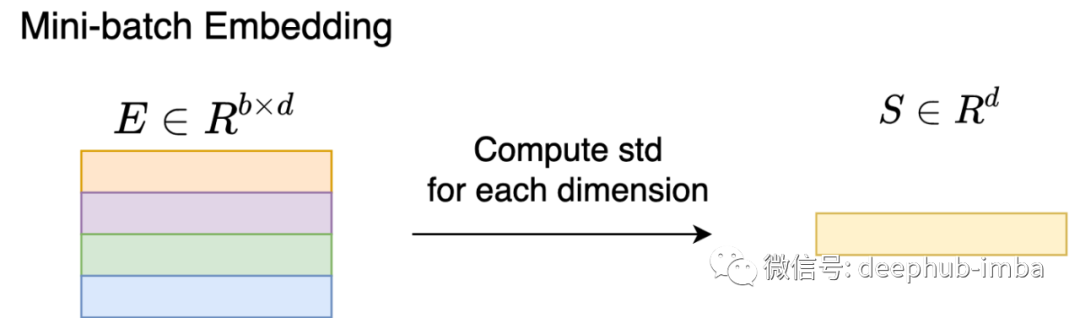
图7:给定特征嵌入矩阵E∈R^{b × d}, VICReg计算维数为d的标准差向量S。标准差作为度量来评估维度的激活。
VICReg中的方差项表示如下:
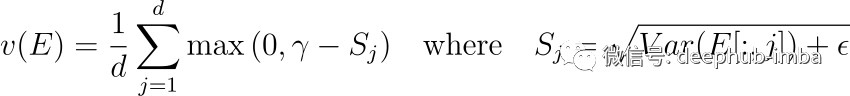
图8:VICReg中的方差项计算特征嵌入矩阵e中各d维的标准差(std),VICReg 鼓励标准差为 γ。ϵ 是一个防止数值不稳定性的小标量。
其中 γ 是一个超参数,表示每维所需的标准偏差,ϵ 是防止数值不稳定性的小标量。
这个公式鼓励标准偏差在每个维度上等于 γ。论文中表示这样做应该可以防止映射到同一向量上的所有输入崩溃。由于嵌入未归一化,VICReg 无法对标准偏差项的范围或界限做出任何假设。VICReg 有两个超参数:与 SVMax 一样的 λ(图 3)和 γ。
基准测试
对于定性的评估,SVMax 和 VICReg 都可以在没有显式负采样的情况下减轻模式崩溃。两个正则化器在不使用训练技巧(如输出量化、梯度裁剪、等)的情况下收敛到非常准确的特征嵌入。两篇论文都来自具有不同计算能力的不同组织。因此,SVMax 评估是比较原始的,而 VICReg 是相对较新的。使用线性分类器在冻结的 ImageNet 预训练网络之上进行微调并对这两个正则化器进行自监督学习的基准测试如下:
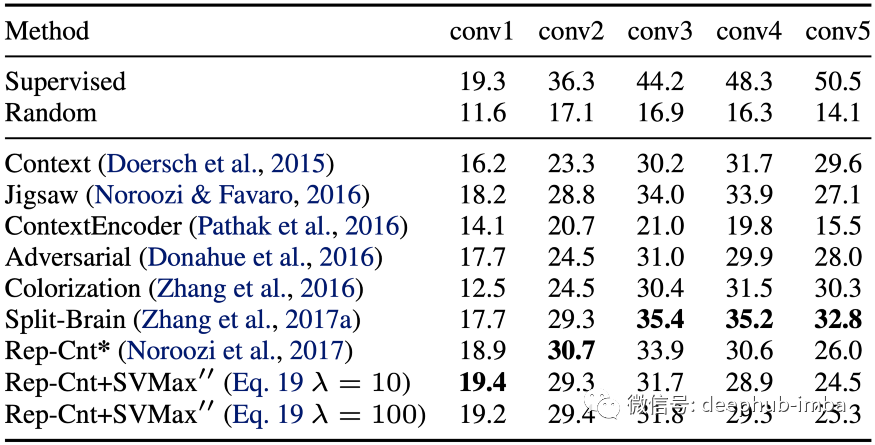
表 1:使用带有 AlexNet 主干的自监督学习的定量 SVMax 评估。通过 ImageNet 分类评估预训练网络 N,并在冻结卷积层之上使用线性分类器。对于每一层卷积特征都会在空间上调整大小,直到剩下的维度少于 10K。在 1000 个对象分类任务上训练一个全连接层,然后是 softmax。
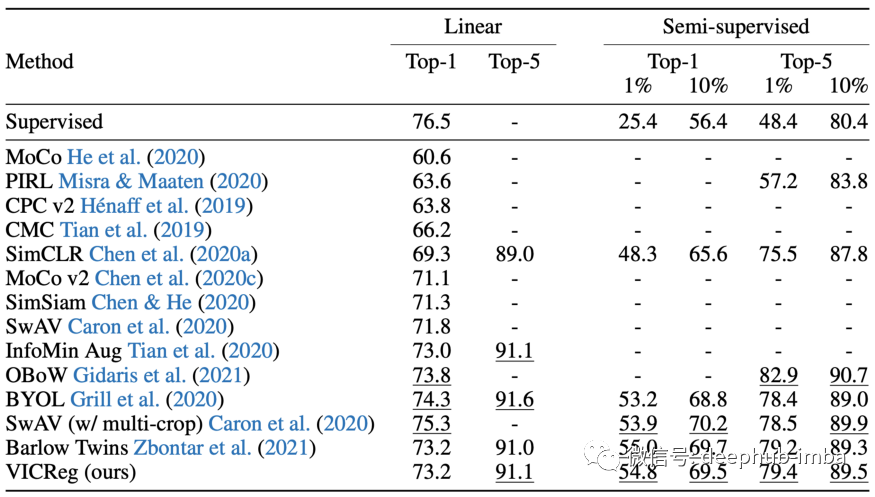
表 2:对使用 VICReg 预训练的 ResNet-50 主干获得的表征进行评估:(1)基于 ImageNet 冻结表征的线性分类;(2) 在来自 1% 和 10% ImageNet 样本的微调表示之上的半监督分类。这里使用了 Top-1 和 Top-5 的准确率(以 % 为单位)。前 3 名最佳自我监督方法使用下划线强调。
VICReg 更专注于自监督学习和模式崩溃问题,而 SVMax 使用监督度量学习可以提供进一步评估。虽然 SVMax 在度量学习中没有达到最先进的结果,但在未调整超参数时它提供了卓越的性能。例如当使用大学习率 (lr) 进行训练时,度量学习方法会学习较差的嵌入和发散。SVMax 使这些监督方法更具弹性,尤其是在学习率较大的情况下,如图 9 所示。
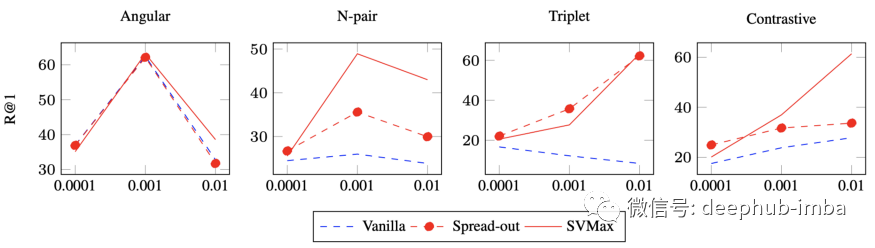
图 9:斯坦福 CARS196 的定量评估。X 和 Y 轴分别表示学习率 lr 和 recall@1 性能。
总结
SVMax 和 VICReg 都是很好的论文。两者都是无监督的,并支持各种网络架构和任务。每个都提供了大量的实验。对特征嵌入文献感兴趣的人强烈推荐这些论文。并且 SVMax 和 VICReg都有PyTorch 的实现。
与 VICReg 相比,SVMax 论文更容易阅读因为它专注于一个想法。相比之下,VICReg 提供了多个概念,其中一个概念是从另一篇论文 Barlow twins 论文中借用的 [4]
与 SVMax 相比,VICReg 对最近的基准进行了大量的定量评估。FAIR 有的是 GPU :)关于权重衰减与特征嵌入正则化器,SVMax 和 VICReg 都对单层的输出进行了正则化。相比之下权重衰减始终应用于所有网络权重(层)。
但是目前还没看到有一篇论文评估这些特征嵌入正则化器在应用于所有层时的影响。如前所述,权重衰减对 [3] 产生了重大影响,我很想知道特征正则化器是否也有类似的影响。
引用
[1] Taha, A., Hanson, A., Shrivastava, A. and Davis, L., 2021. SVMax: A Feature Embedding Regularizer.
[2] Bardes, A., Ponce, J. and LeCun, Y., 2021. Vicreg: Variance-invariance-covariance regularization for self-supervised learning.
[3] Power, A., Burda, Y., Edwards, H., Babuschkin, I. and Misra, V., 2021. Grokking: Generalization beyond overfitting on small algorithmic datasets.
[4] Zbontar, J., Jing, L., Misra, I., LeCun, Y. and Deny, S., 2021. Barlow twins: Self-supervised learning via redundancy reduction.
作者:Ahmed Taha