SHA-3
SHA-3的历史

2015年通过公募展SHA-3选出了一个名为KECCAK的哈希函数,作为SHA-3的代表。因此这两个名字代表着同一个哈希函数。
在SHA-3面世之前,SHA-1被广泛使用。SHA-1被王小云教授破解后,MD系列的哈希函数不再安全,此后SHA-3被要求使用非MD系列的哈希函数。SHA2虽然目前阶段仍然使用中,但是由于SHA-2和SHA-1是同样的动作原理,都是MD系列的构造,因此基于王教授的研究可能不再安全。即非MD系列的哈希函数需求下创生了SHA-3。
这种新的构造被称为海绵结构,海绵结构不仅使用在哈希函数领域,更在其他多个领域被使用,有效率和安全的保障。

SHA-3项目开启后,从08年提交的64个哈希中,根据层选,经历了51,14,5的选拔,最终KECCAK被选拔。选择的标准是安全性,可用性和效率。五个final-list的哈希函数还是有必要了解一下名字的。15年基于KECCAK提出了SHA-3算法,可以理解为KECCAK的某些特殊情况下的某些特殊参数的作用形式。
XOF函数:同时公布了两种XOF函数SHAKE128,256, 这种函数是可用让输出值的长度变为任意长度的算法。
那么为什么KECCAK最终获胜了,它的优势有哪些?
- 海绵结构:像海绵一样,能够很好的吸收水分份和很好的挤出水分。具体结构会在后面分析
- 性能:软件层面性能表现不错,硬件层面性能远胜于其他优胜候补
- 安全性:提供了哈希安全三要素(抗碰撞性,第一、第二原像抗性)的同时,还对侧信道攻击具有抗性。
海绵结构

像海绵一样有吸水和出水两个过程。因此有吸收和输出两个阶段。
首先最重要的是padding。即为了满足哈希函数 输入条件,需要扩张某些数据的末尾来凑够位数,如1024bit的块处理。
吸收阶段:然后把处理后的数据块分段加入如图所示的步骤中,每次输入的bit数都是相等 ,都是r bit。输入的长度相等,且对于函数f而言,输入和输出的长度也相当。这里区别于MD系列输入的位数大于输出,这里是前后一致的,输入和输出都是r+c bit。这个过程中还有KECCAK-p[1600,24]这个参数参与运算。
输出阶段:每次输出长度等于r bit的数据。
海绵构造中最重要的三个参数是函数f,padding方法pad,和rate r。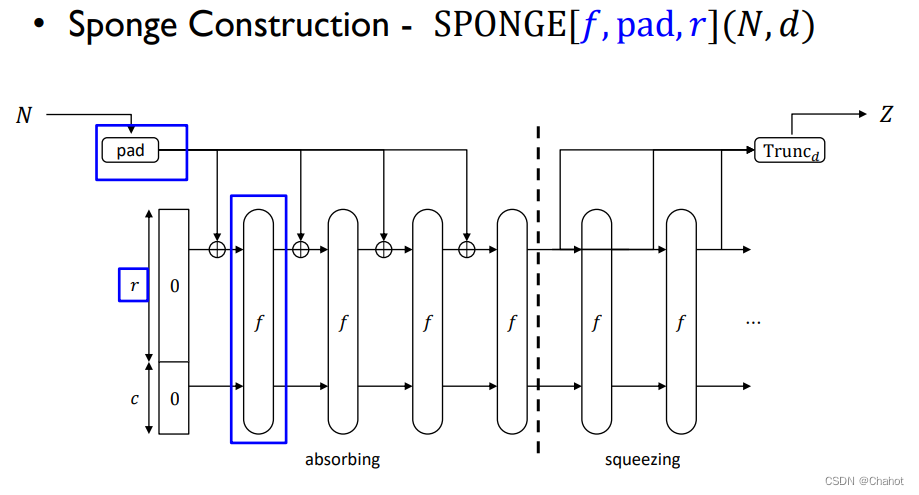
SPONGE(f,pad,r)[N,d]这样的构造下最终输出Z是哈希函数。其中N是任意位数的信息,d是输出的哈希值的长度。
函数F中线性函数和非线性函数需要适当的加入和调整才能保住输入和输出的长度相等。
b=r+c,它被称为f的宽度。r是输入的位数被称为rate,r越大意味着输入的数据位数越来越多。c是b-r,是用来调整输入长度的参数,c越大,如果r是固定的,意味着f函数要求的输入位数变多,此时需要调整输入的长度,主要作用就是用来调整的。
吸收阶段与输出阶段
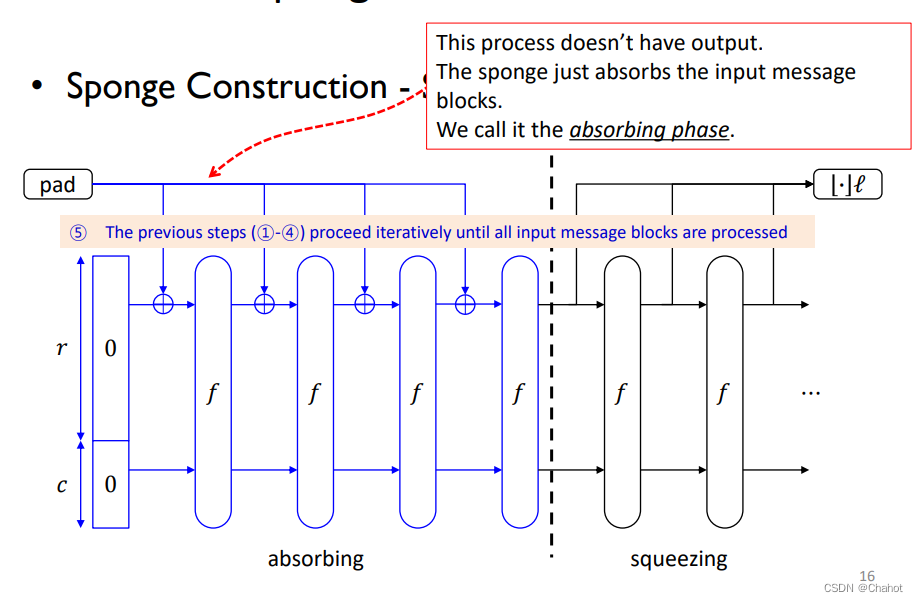
从结构上而言,吸收阶段的输入数据的任意比特分成n次,每次以r比特输入。总输入的位数是n*r,然后每次输入的函数会在xor运算后直接输入函数f,然后调节参数c也会输入函数f,最终产生两个输出,位数分别是r和c。经历n轮这样相同的运算后,所以的需要的数据已经全部输入,此时开始准备输出。
输出也是分轮次输出,每次输出rbit然后在某一时刻将所有的得到输出连接起来,每个输出的长度为r bit。
到此为止海绵结构的运作原理都已经理解了,注意r和c的初始值都是0即可。
接下来理解一下算法。
f的定义为使用函数 keccak-p[1600,24]
pad使用的算法为Multi-rate
r和c只要定义其中一个就可以求出另一个,因此这里定义c为
l
e
n
(
d
i
g
e
s
t
)
∗
2
len(digest)*2
len(digest)∗2,假设输出的哈希值最终是224,那么这个c=448,那r=1600-448=1152
算法整体的先定义各种参数,P是全体输入,根据N的输入进行padding,然后确定输入轮次n,无非就是最终padding后的程度除以r即可。然后就可以得到c和b。重复步骤7和8进行哈希运算,最终的要一个r的组合体Z,然后将Z剪切到d bit即可。整个过程和之前的图示是相同的。
双工海绵
这是一个吸收和输出阶段同时进行的构造,效率更高。在认证密码和随机数生成时被广发使用,输入和输出的长度是相等的。
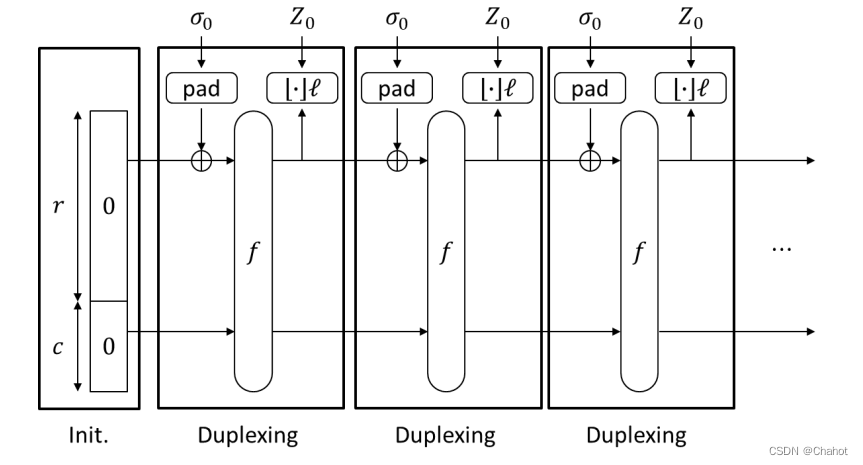
如图所示,输入padding后的数据后进行xor运算并通过函数f,输出值立刻输出成Z。输入与输出的间隔非常短,只有一个f函数的流程。
KECCAK-p

这个函数内有两个参数,分贝是b和n。其中b的选值从上述数组中任选其一即可。
KECCAK函数是一个块函数,她的整体构造也是呈三维立体状的、总结而言有下图所示的函数步骤。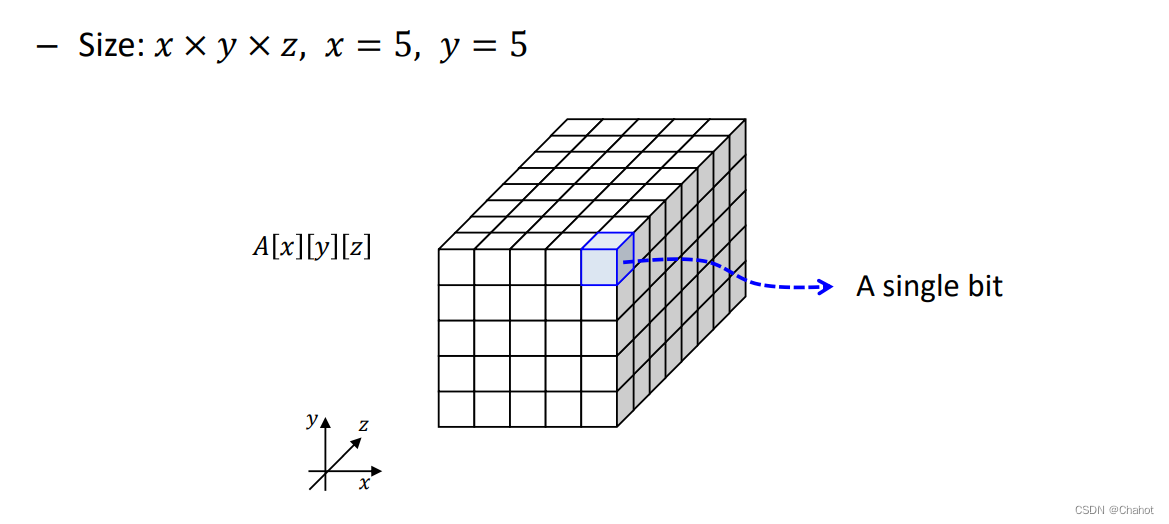
其中三维模型中,xy固定为5,只有深度不同,深度被称为lane。这个根据lane 的长度决定这个三维物体的深度。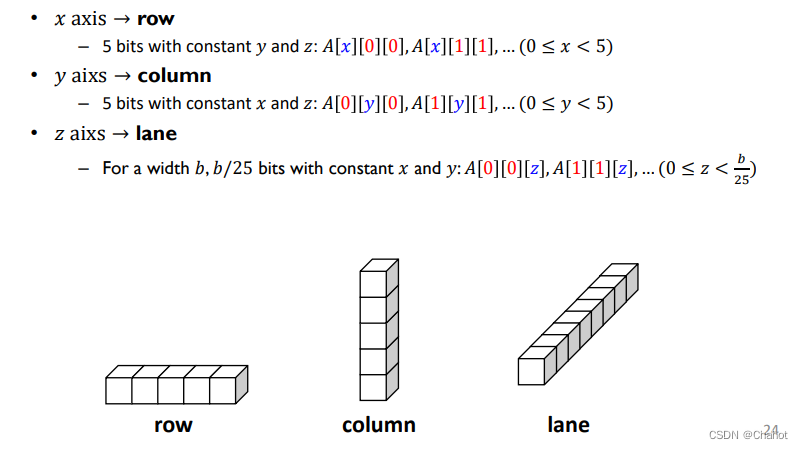
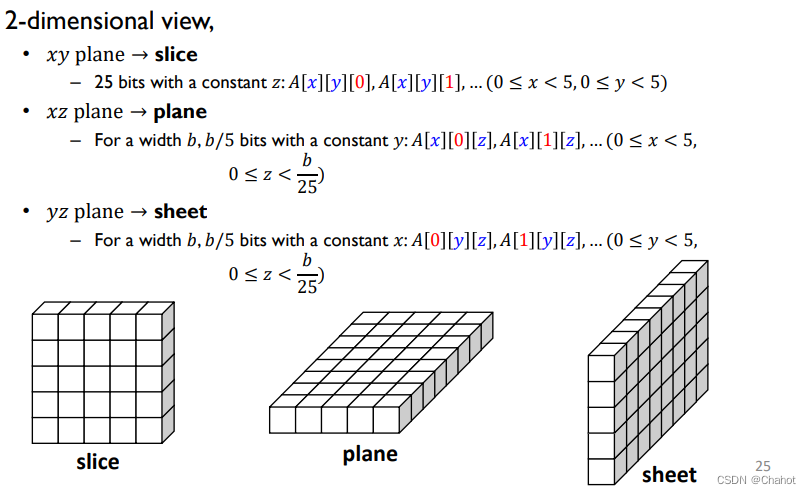
上两个图是在一维和二维的情况下一些形容xyz方向的术语表达。
其中的函数
θ
\theta
θ: 将两个列进行XOR运算并获得一个1bit单位
ρ
ρ
ρ:对一个lane中的某个bit进行旋转
π
π
π:将一个slice根据lane进行重新排序,可以理解为对slice的重新排序
χ
\chi
χ:非线性运算,将行的值变为其他值
ι
\iota
ι: 讲一个立方体里的某个lane根据i这个index进行和与其他数值的xor运算从而变化其值
θ
\theta
θ
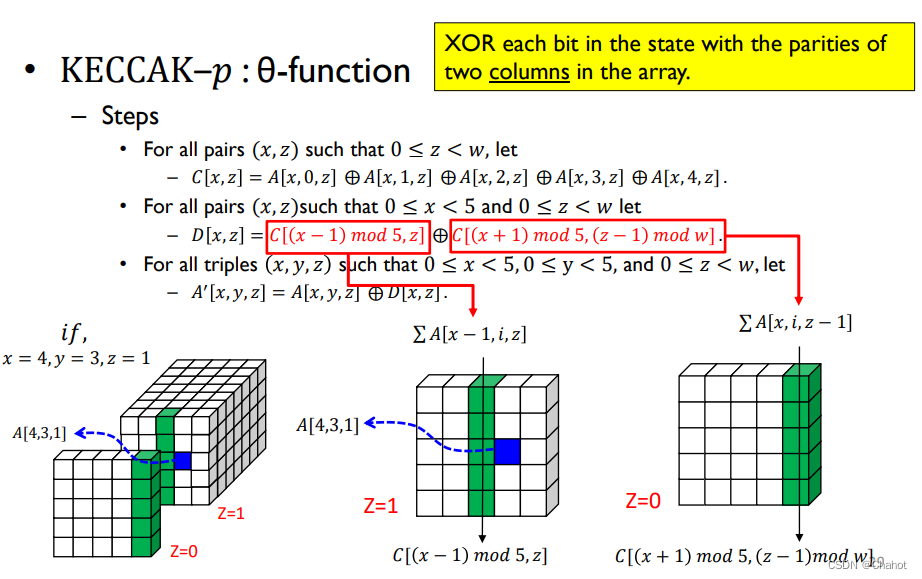

这是将两列的数据拿出来然后求XOR到一个值,然后将这个值替换到目标的一个单位bit上,步骤如上。
ρ
ρ
ρ

这个函数从图片上理解可能会有些复杂,需要用数式一起理解。w是width的缩写,即lane的长处,t是一个临时变量。ρ[8]的8是指w=8.
此时代入上面的公式进行的计算结果。z是位于区间[0-7]的整数。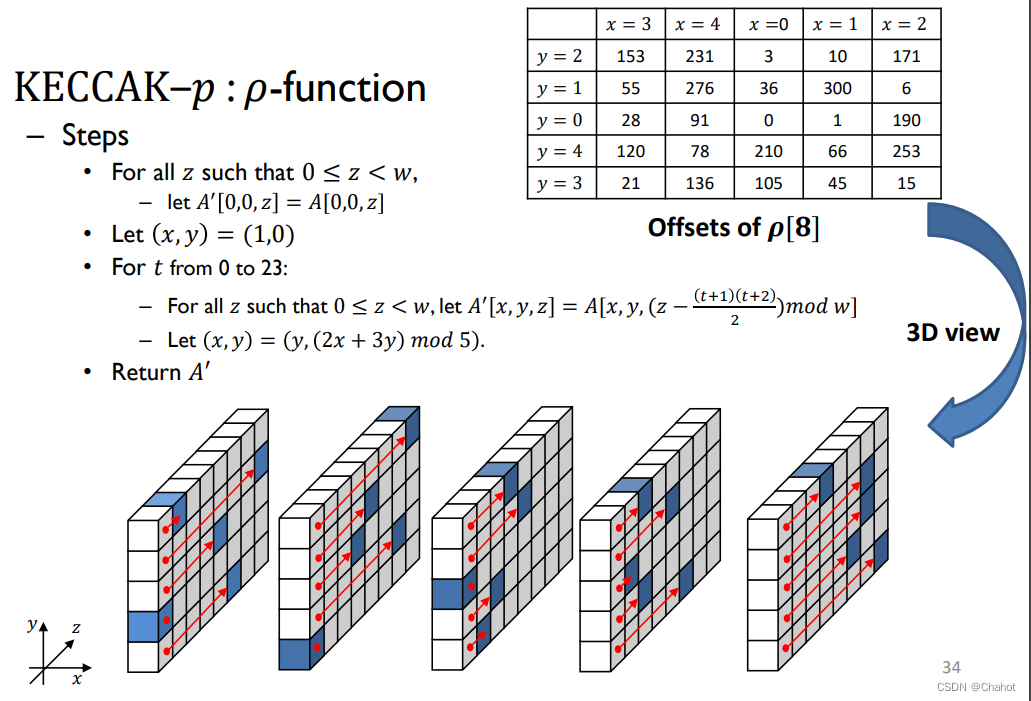
x=1,y=0时,代入公式计算可得offset移动量为1。换言之每个单位比特,图中的最小方块向lane方向移动一格,如果是最后一个位置则移动到最前方的位置。
这个函数运算完毕后,每个sheet的所有单位lane中的单位bit都会发生一定顺序的位移。
π
π
π
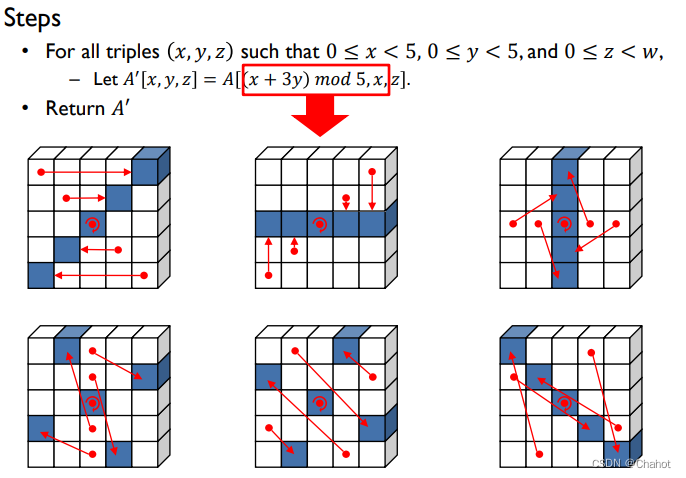
之前的定义说了这是一个根据slice来旋转lane的方法,为了好理解不妨把slice改为的lane长度设为1,则剩下的所有lane聚合到可视的第一面中。如图所示,本质上是一种旋转
图1表示的是对角线旋转九十度后的到达蓝色对角线的样子,图2表示的是对角线旋转45度后水平的样子,图3表达的是旋转九十度后的样子。图四45度,图5九十度,图6不是旋转,但是是对中心点的中心对称变化,这是一个基于硬件的变化,因此这个函数与其他四种函数不同在硬件上的实现效果要比软件上好得多。
χ
\chi
χ
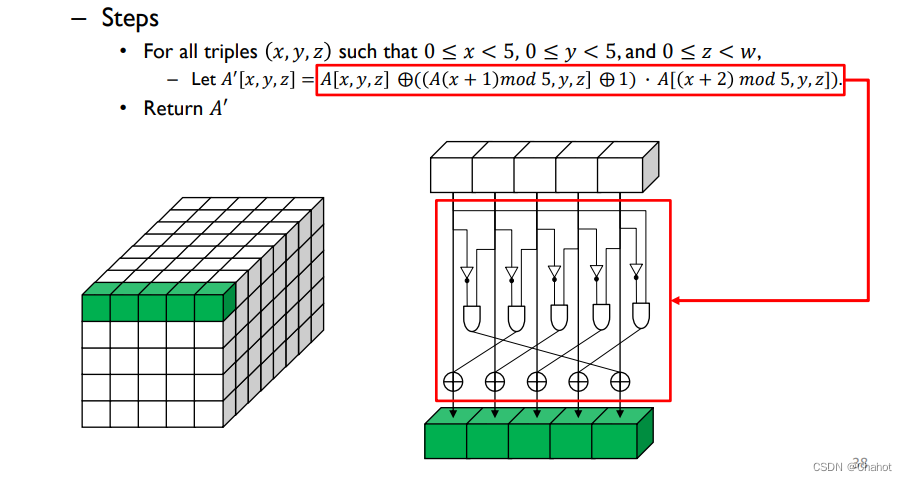
通过图示的方法将一个行的所有数值进行更新。
ι
\iota
ι

这是一个更新lane值的函数,具体的过程如下:
t是一个八位二进制数,而图中的lane也是一个8位数组。令R=1000 0000并用数字零放在R的前面连接他形成一个9位二进制数。这个二进制的某些位数去做一些更新,使用xor运算,更新后再以附加位为基准,将R的多出的位数剪切掉,最终返还R的0号index所指向的数据。
Multi-rate padding

这是一个很简单的padding方法,在需要padding 的尾部后空出两位,然后追加10…01的组合,中间由n个需要的0组成。
如上图所示,加入输出长度d=224,c=2d,则c=448。那么r=1600-448=1152。空出来 两位填入01后追加10…01的padding。这就是这个算法的全部内容。这里空出来的两位被称为suffix,在SHA3哈希里的值被定为01,在SHA3XOF中被定义为1111。
总体而言,本文涉及到的KECCAK函数原理如图所示。
这里简单提及一下SHA-3XOF,简单来说就是M后追加1111的二进制数后参与的KECCAK运算。和SHA-3区分即可。
版权归原作者 Chahot 所有, 如有侵权,请联系我们删除。