【数据结构】堆排序、TopK问题(堆的应用)

文章目录

五.堆排序

前言

既然最近学习了堆，堆的一个重要应用就是进行堆排序，这里提一下：堆排序即快排的一种。在后面的学习中，我们会学习很多排序方法。今就向各位浅谈下快排之一：堆排序 ，堆排序即利用堆的思想来进行排序。

• 假如我们有一串乱序数组，如下：

14，2，8，6，20，13，7，1

现在想要对它进行排序，应该怎么做呢？

法一.直接建堆排序

上篇文章，我们模拟实现了堆，实现后即可对一串乱序数组进行堆排序。假设我们排升序，且堆为小根堆。实现过程非常简单。

首先，把数组的每个元素（HeapPush）插入到堆中。

其次，我们知道小根堆的堆顶是最小的数字，依次遍历堆顶（HeapTop）的元素，将堆顶元素赋值到数组里，从下标0开始，赋值后删除（HeapPop）堆顶元素，++数组下标。此时堆就会重新调整，最终堆顶依旧是最小的，再重复上述赋值堆顶到数组的操作，直到堆为空（isHeapEmpty）

//堆排序 --- 升序voidHeapSort(int* a,int size){//创建堆结构并初始化
    HP hp;HeapInit(&hp);//将数组元素插入堆中for(int i =0; i < size; i++){HeapPush(&hp, a[i]);}//依次遍历，取堆顶赋值数组，++下标，删除堆顶元素，依次循环，直至堆为空size_t j =0;while(!HeapEmpty(&hp)){
        a[j++]=HeapTop(&hp);HeapPop(&hp);}//记得销毁动态开辟空间HeapDestroy(&hp);}intmain(){int a[]={14，2，8，6，20，13，7，1};HeapSort(a,sizeof(a)/sizeof(int));//实现堆排序for(int i =0; i <sizeof(a)/sizeof(int); i++){printf("%d ", a[i]);//打印}printf("\n");return0;}

运行结果：

复杂度分析

for(int i =0; i < size; i++){HeapPush(&hp, a[i]);}while(!HeapEmpty(&hp)){
    a[j++]=HeapTop(&hp);HeapPop(&hp);}

时间复杂度：O(N*logN)

空间复杂度：O(N)

for循环的时间复杂度为O(N* logN)，因为HeapPush函数的内部执行过程就是把数组的每个元素插入堆中，有N次。接着，每插入一个数据都要重新向上调整（AdjustUp）高度次以确保为堆形态，每个元素都要调整高度次，高度为logN，综上此段为O(N*logN)。while循环的时间复杂度也是O(N * logN)，原理类似，这里不过多赘述。

综上，时间复杂度为O(N*logN)，确实比我们先前的冒泡排序O(N^2)要快不少。但是，这个方法排序是不够好的，因为难道说为了实现堆排序还要自己手写一个完整的堆吗？这么复杂的实现堆的过程还不如不用堆排序了，而且这种方法的空间复杂度也非常大，达到了惊人的O(N)。原因是实现堆的过程是动态开辟的，数组有多少元素，就开辟能够存储这些元素的空间，所以空间复杂度自然是O(N)。

可不可以换一种更好的方法，但同样是利用堆的思想实现快排呢？

法二.直接对数组建堆

前面我们已经知晓，完全二叉树的存储形式为数组，为什么还要实现一个堆呢？直接把数组改成堆难道不香嘛？由此我们相处直接对数组建堆。

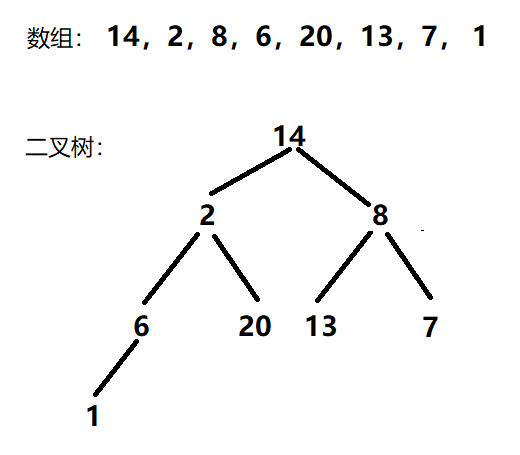
接下来，我们就要进行建堆了，有两种方法：

1. 使用向上调整建堆，插入数据的思想建堆
2. 使用向下调整建堆

向上调整建堆

首先，我们把第一个数字看成堆，当第二个数字插入进去的时候，进行向上调整算法，使其确保为小堆，向上调整的算法在上篇博文已详细讲解过，不过多赘述。具体插入数据过程就是遍历数组，确保数组里每一个数进行向上调整算法。

图解：

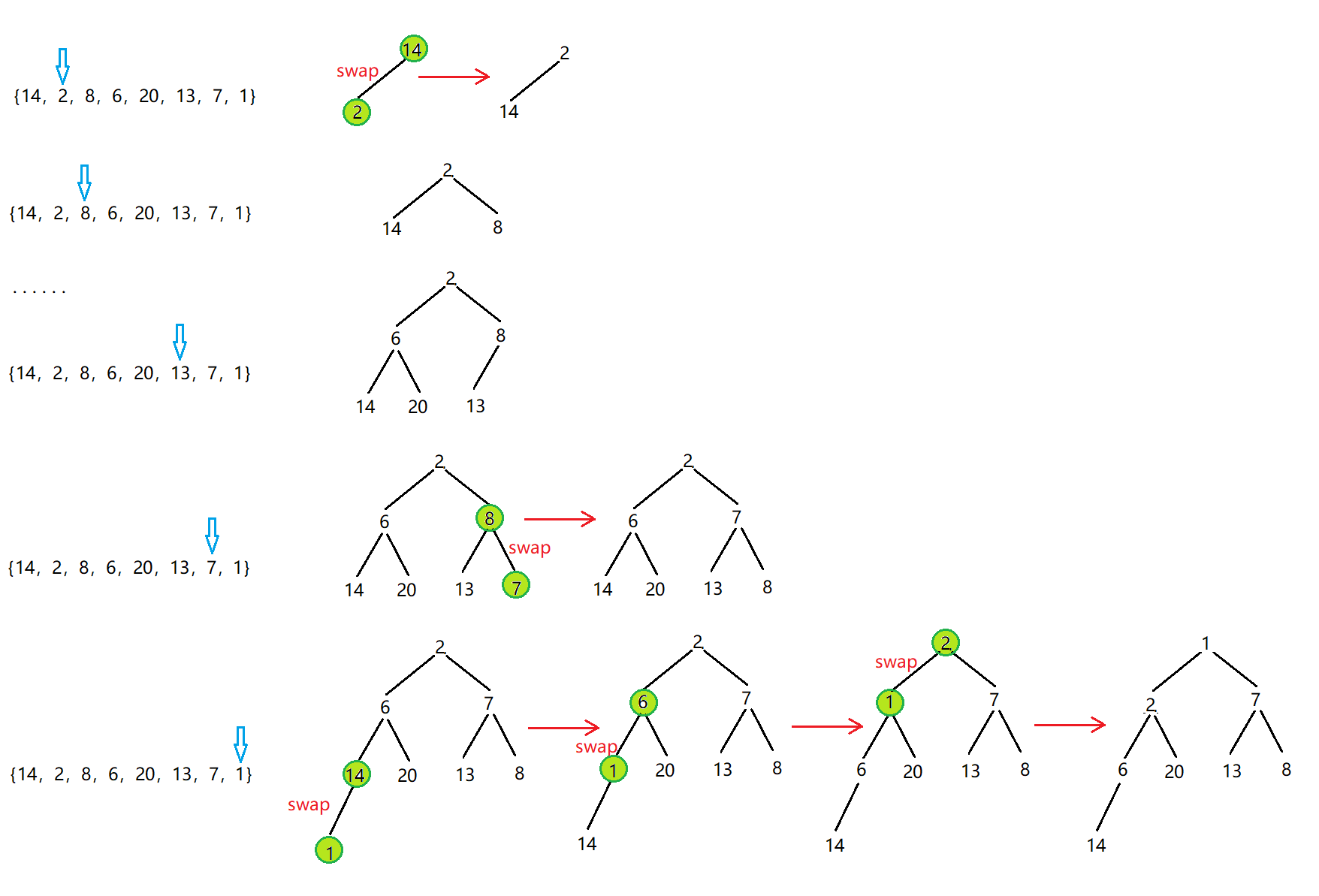
代码：

//交换voidSwap(int* pa,int* pb){int tmp =*pa;*pa =*pb;*pb = tmp;}//向上调整算法voidAdjustUp(int* a,int child){int parent =(child -1)/2;while(child >0){//if (a[child] > a[parent]) //大根堆if(a[child]< a[parent])//小根堆{Swap(&a[child],&a[parent]);
            child = parent;
            parent =(child -1)/2;}else{break;}}}//升序voidHeapSort(int* a,int n){//建堆//1.向上调整int i =0;for(i =1; i < n; i++)//应该从i=1时遍历，因为第一个数据在堆里不需要调整，后续再插入时调整{AdjustUp(a, i);}}intmain(){int a[]={14，2，8，6，20，13，7，1};HeapSort(a,sizeof(a)/sizeof(int));for(int i =0; i <sizeof(a)/sizeof(int); i++){printf("%d ", a[i]);}return0;}

运行结果：

向下调整建堆

问题：能直接进行向下建堆吗？
答案：不能

解析：首先回顾下使用向下调整的前提是什么？必须得确保根结点的左右子树均为小堆才可，而我们创建的数组为乱序的，无法直接使用向下调整。

解决办法：从倒数第一个非叶结点开始向下调整，从下往上调
分析：从该解决方案中，我们首先要找到这个倒数第一个非叶结点的数在哪？其实最后一个结点的父亲即为倒数第一个非叶结点。当我们找到这个非叶结点时，把它和它的孩子看成一个整体，进行向下调整。调整后，再将次父节点向前挪动，再次向下调整，依次循环下去。

再回顾下父亲和孩子间的关系：

1. leftchild = parent * 2 + 1
2. rightchild = parent * 2 + 2
3. parent = (child - 1) / 2

图解：

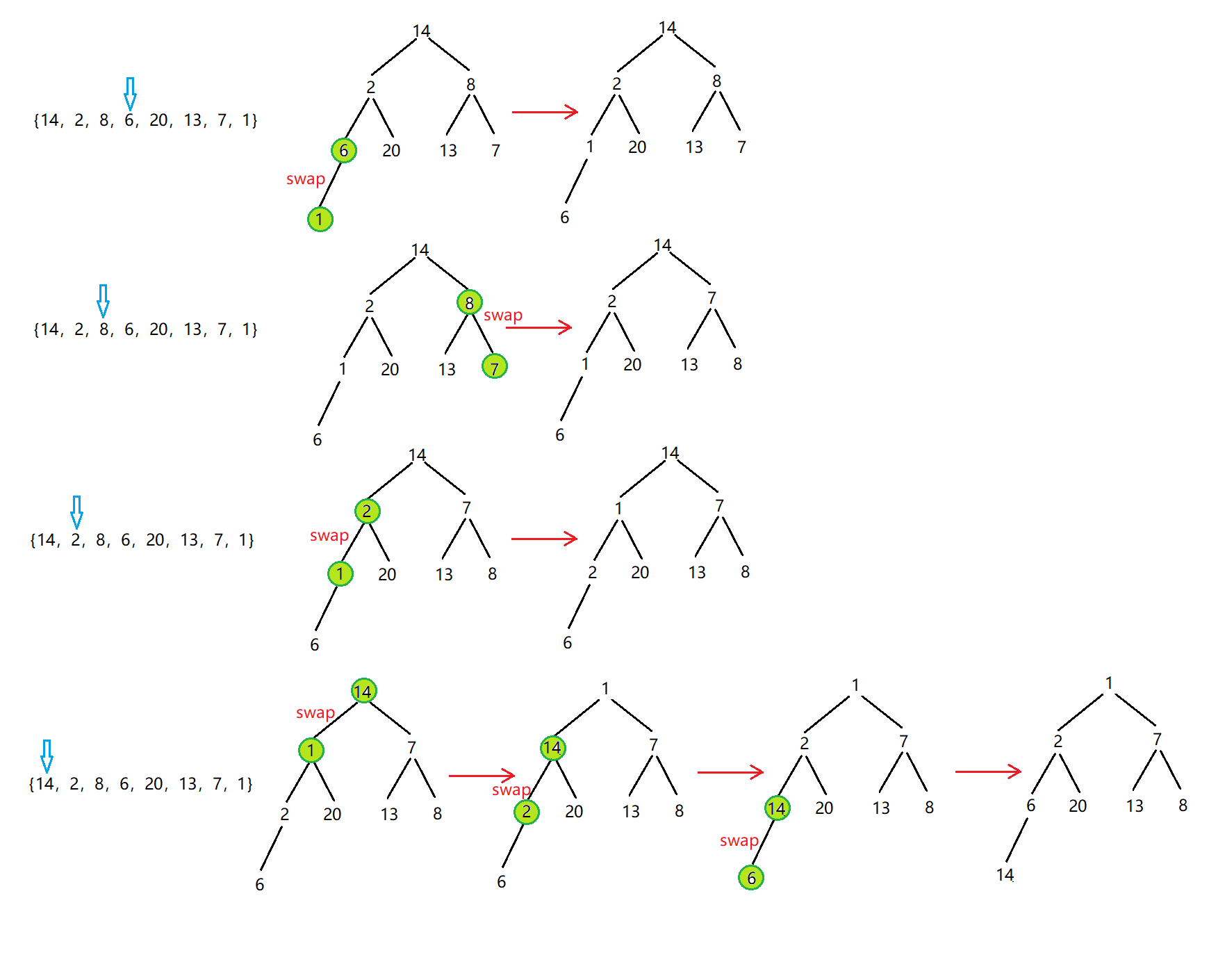
代码：

//交换voidSwap(int* pa,int* pb){int tmp =*pa;*pa =*pb;*pb = tmp;}//向下调整算法voidAdjustDown(int* data,int n,int parent){int child =2* parent +1;//计算子节点//当子节点调整到堆尾时结束循环while(child < n){//找出较小的子节点if((minChild +1)< n && data[minChild]> data[minChild +1]){
            minChild++;}//如果父节点大于较小的子节点就交换if(data[minChild]< data[parent]){Swap(&data[minChild],&data[parent]);
            parent = minChild;
            minChild =2* parent +1;}else{break;}}}//升序voidHeapSort(int* a,int n){//建堆//2、向下调整for(int i =(n -1-1)/2; i >=0; i--){AdjustDown(a, n, i);}}intmain(){int a[]={14，2，8，6，20，13，7，1};HeapSort(a,sizeof(a)/sizeof(int));for(int i =0; i <sizeof(a)/sizeof(int); i++){printf("%d ", a[i]);}return0;}

运行结果：

建堆复杂度分析

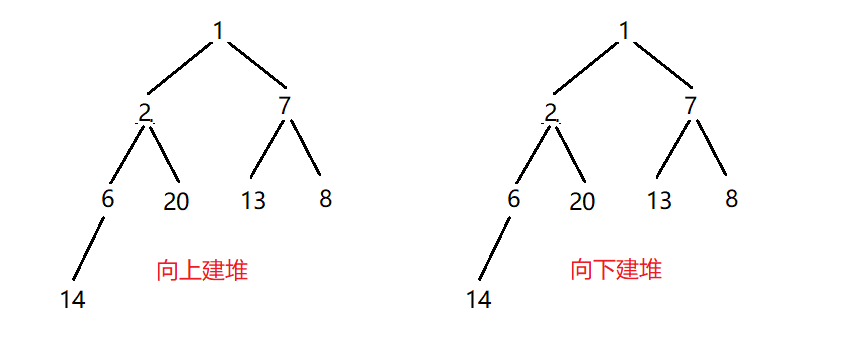
从上图中，我们可以看出，使用不同的方式建堆最后的样子是相同的，其实这里出现了一个巧合，向上建堆和向下建堆最后的结果有可能不一样，那哪种方式好呢？下面我们从复杂度来分析那种方式好。

向上调整建堆

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个节点不影响最终结果)：

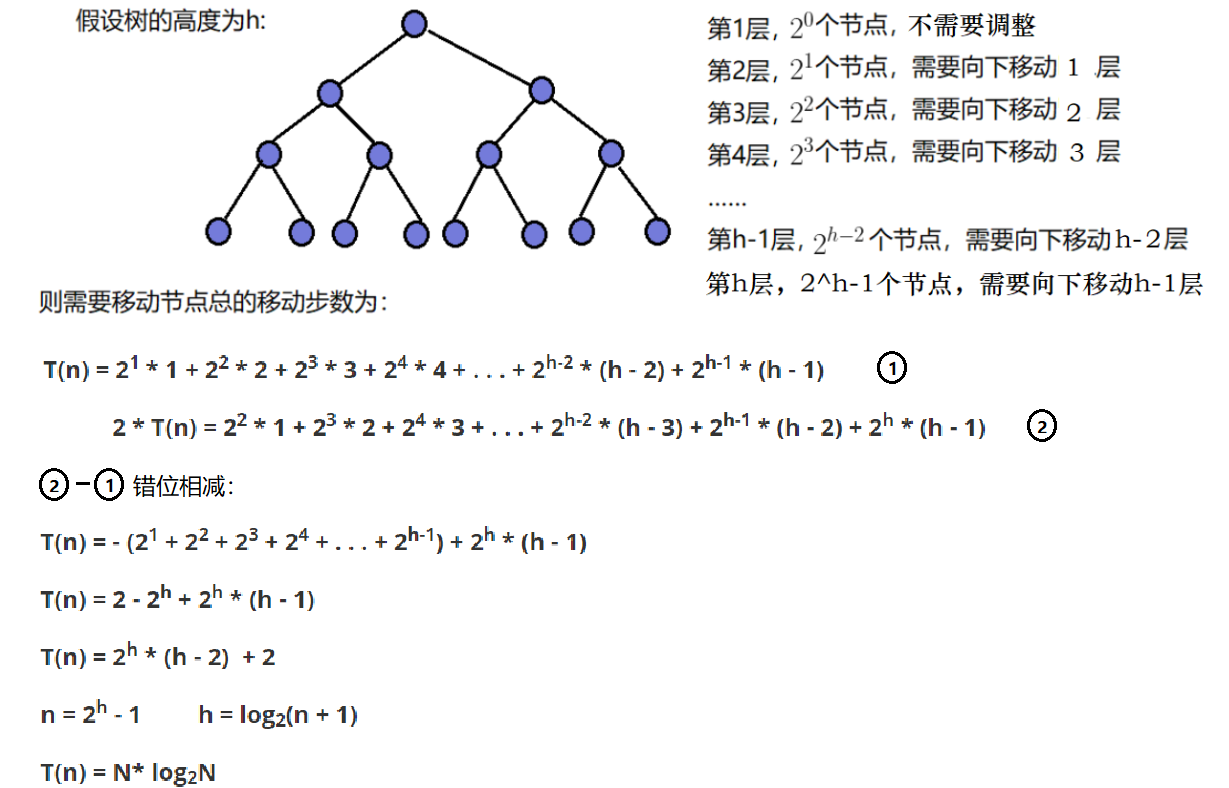
如上图，最终可以得到向上调整建堆的时间复杂度为：*O(NlogN)**；

向下调整建堆

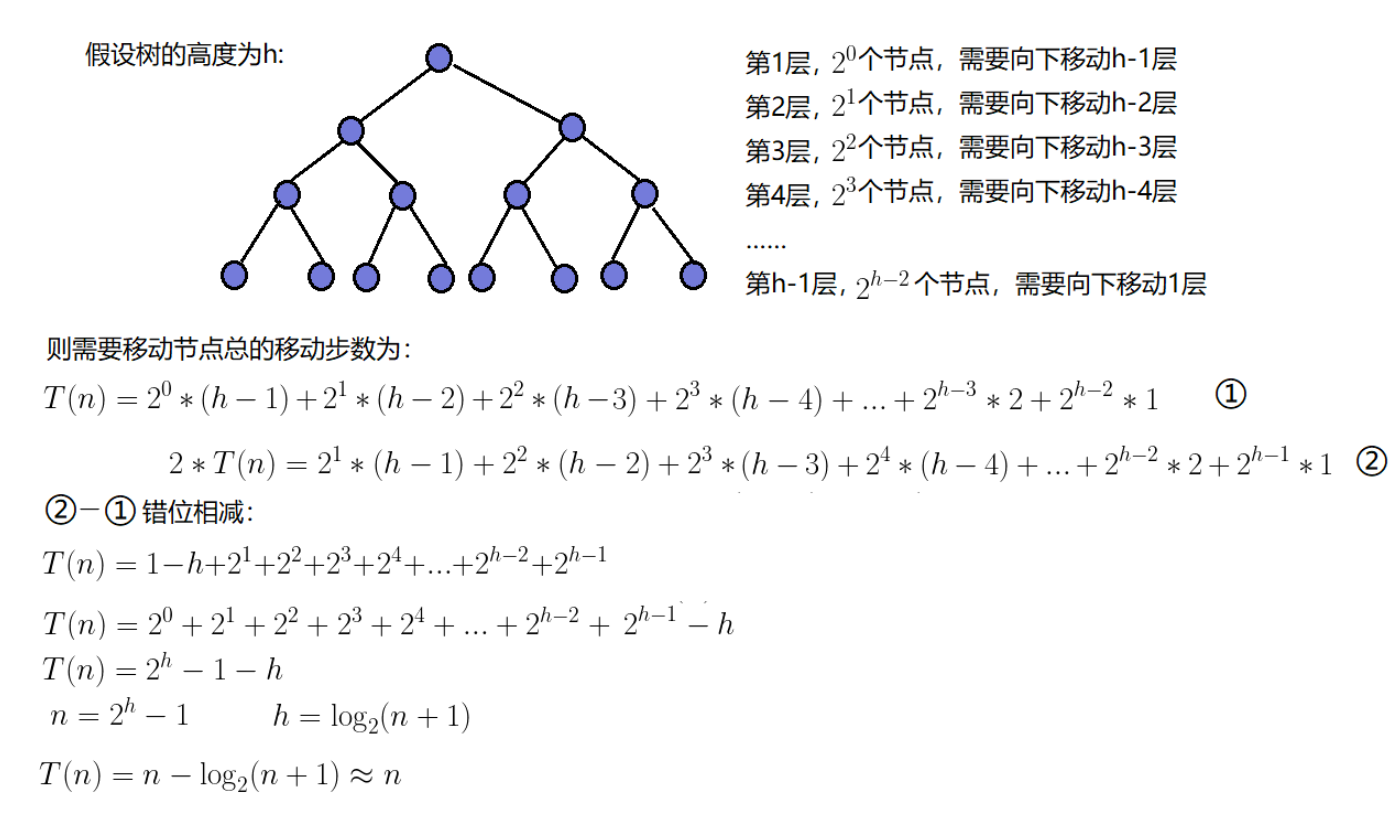
如上图，向下调整建堆的时间复杂度为：**O(N)**；

综合上面两种建堆方法，**建堆的时间复杂度为：O(N)**；

对比：

通过上述计算，我们得到如下：

1. 向上建堆：O(N*logN)
2. 向下建堆：O(N)

由此可见，使用向下建堆的方式更优，其时间复杂度较小。当然，使用向上建堆也是可以的，只不过向下建堆更好一点。

升序能否建小堆？

答案：不能

解释：从上文我们已经知道建堆用向下建堆是比较优的，为O(N)，并且建好堆后第一个位置的数字即为最小的，此时第一个数字已经确定了并且是最小的，但如若使用小堆的话，也就是需要从第二个数字开始往后看成一个堆，此时关系就全乱了，不再符合小堆的性质，此时也就意味着我们需要从第二个数字往后重新向下建堆，以确保此时的堆顶也就是数组第二个元素为次小的，并以此类推重新建堆确保第三个次小的，依次循环下去……如果这样做，还不如直接遍历选数!太复杂了。

解决方案：升序建大堆

选数排序（建大堆）

先看下建好大堆的样子：

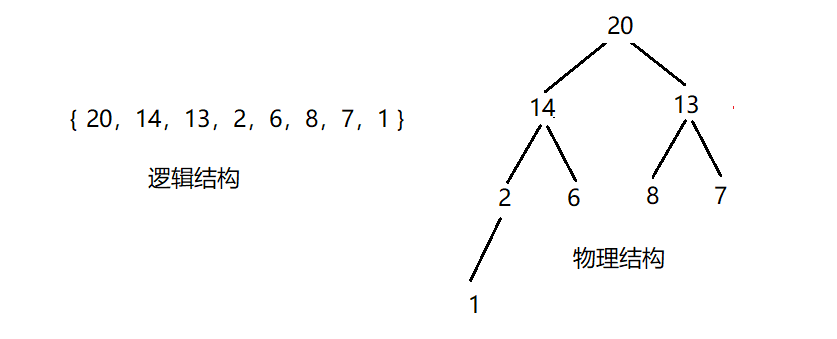
思路：

首先，得明确我们建堆后，此时堆顶就是最大的数据，现在我们把第一个数字和最后一个数字交换，把最后一个数字不看做堆里的，只需要数组个数N–即可。此时的左子树和右子树依旧是大堆，再进行向下调整即可。

画图解析过程：

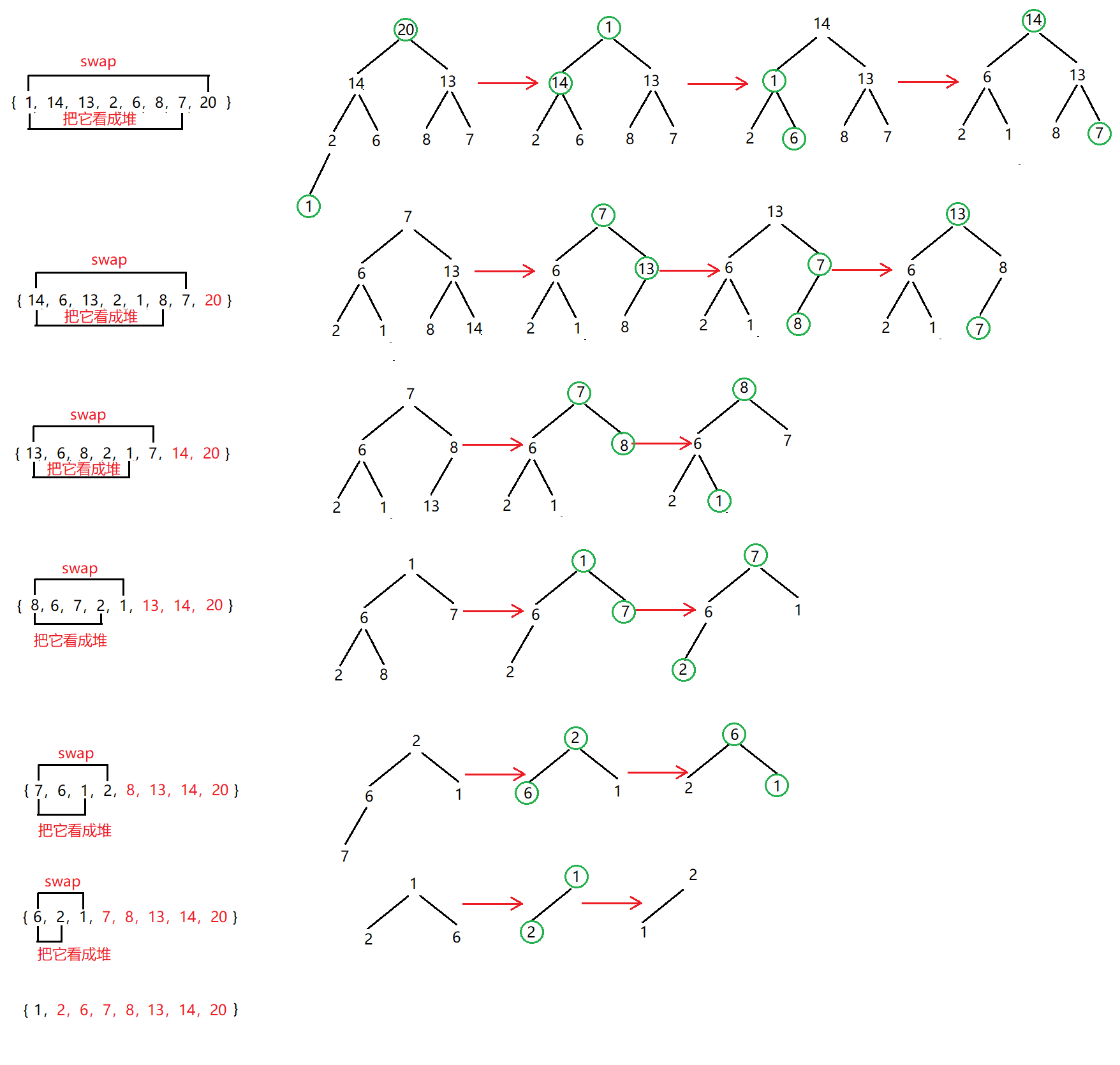
//交换两个节点voidSwap(int* p1,int* p2){int tmp =*p1;*p1 =*p2;*p2 = tmp;}//向上调整 -- 大堆voidAdjustUp(int a[],int child){int parent =(child -1)/2;//找出父节点while(child >0)//当调整到根节点时不再调整{if(a[parent]< a[child]){Swap(&a[parent],&a[child]);}else{break;}//迭代
        child = parent;
        parent =(child -1)/2;}}//向下调整 -- 大堆voidAdjustDown(int a[],int n,int parent){int maxchild = parent *2+1;//找到左孩子（左孩子+1得到右孩子）while(maxchild < n)//调整到数组尾时不再调整{if(maxchild +1< n && a[maxchild +1]> a[maxchild]){
            maxchild +=1;}if(a[parent]< a[maxchild]){Swap(&a[parent],&a[maxchild]);}else{break;}//迭代
        parent = maxchild;
        maxchild = parent *2+1;}}voidHeapSort(int a[],int n){//建堆 -- 向上调整建堆：O(N*logN)//int i = 1;//for (i = 1; i < n; i++)//{//    AdjustUp(a, i);//}//建堆 -- 向下调整建堆：O(N)for(int i =(n -1-1)/2; i >=0; i--)//n-1找到最后一个叶节点，该节点-1/2找到倒数第一个父节点{AdjustDown(a, n, i);}//排序 -- 升序（建大堆，向下调整）：O(N*logN)//选数for(int i = n -1; i >0; i--){Swap(&a[i],&a[0]);//交换堆尾和堆顶的元素AdjustDown(a, i,0);//向下调整}}intmain(){int a[]={15,1,19,25,8,34,65,4,27,7};int n =sizeof(a)/sizeof(a[0]);//堆排序HeapSort(a, n);for(int i =0; i < n; i++){printf("%d ", a[i]);}return0;}

六.TopK问题

TOP-K问题：N个数里面找出最大/最小的前k个。一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，我们能想到的方法有很多，如下：

1. 排序 – 时间复杂度：O(N * logN) 空间复杂度：O(1) – 要求进一步优化。
2. 建立N个数的大堆，Pop K次，就可以找出最大的前K个 – 时间复杂度：O(N+logN*k) 空间复杂度：O(1)

问题：
有可能N非常大，以至于远大于K。比如100亿个数里面找出最大的前10个。此时上面的方法就不能用了，因为此时会导致内存不够。就好比我现在想知道100亿个整数需要多少空间？

1G = 1024MB
1024MB = 1024 * 1024KB
1024 * 1024KB = 1024 * 1024 * 1024Byte ≈ 10亿字节
一个整数4个字节，100亿个整数400亿个字节，≈40G
40个G内存根本放不下，说明100亿个整数是放在磁盘中的，也就是文件中。由此得知上述方法不得行，得寻找一个更优解。

解决方案：
用前K个数建立一个K个数的小堆，然后剩下的N-K个依次遍历，如果比堆顶的数据大，就替换它进堆（向下调整），最后堆里面的K个数就是最大的K个。

复杂度： 时间复杂度：O(K + logK * (N-K)) 空间复杂度：O(K)

实现过程:

//创建一个文件，并且随机生成一些数字voidCreateDataFile(constchar* filename,int N){
    FILE* Fin =fopen(filename,"w");if(Fin ==NULL){perror("fopen fail");exit(-1);}srand(time(0));for(int i =0; i < N; i++){fprintf(Fin,"%d ",rand()%10000);}}//建堆，选前K个最大的数并且打印voidPrintTopK(constchar* filename,int k){assert(filename);
    FILE* fout =fopen(filename,"r");if(fout ==NULL){perror("fopen fail");exit(-1);}//小堆int* minHeap =(int*)malloc(sizeof(int)* k);if(minHeap ==NULL){perror("malloc fail");exit(-1);}//读前K个元素for(int i =0; i < k; i++){fscanf(fout,"%d",&minHeap[i]);}//建k个数的堆for(int j =(k -1-1)/2; j >=0; j--){AdjustDown(minHeap, k, j);}//读取后N-k个int val =0;while(fscanf(fout,"%d",&val)!=EOF){if(val > minHeap[0]){
            minHeap[0]= val;AdjustDown(minHeap, k,0);}}for(int i =0; i < k; i++){printf("%d ", minHeap[i]);}printf("\n");free(minHeap);fclose(fout);}intmain(){int N =10000;constchar* filename ="Data.txt";int k =10;CreateDataFile(filename, N);PrintTopK(filename, k);return0;}