DFS篇--入门须知

** 🐏小羊简介：**

---

💖博客主页：小羊不会飞

🚀年龄：20 大二在读

💪爱好：干饭，运动，码代码，看书，旅游

📃即将更新：

🎯1、BFS算法

🎯2、手把手带你搭建个人博客网站

🚍：感兴趣的朋友，赶紧上车吧！！

🎉欢迎关注🔍点赞👍收藏🎇留言📙

🎄有任何疑问，欢迎留言讨论！！！

---

前言：

   啊啊啊，小羊开更了，最近忙完了软著的事情（见下图），接下来终于开始准备算法的学习了，如果有时间的话，博主打算寒假出一期"手把手创建网站"的博客，感兴趣的小伙伴欢迎关注💖！

   好了，回归正题，博主最近学习了一下**DFS算法**，也算是弄清楚了上个学期的一些小疑惑吧，刷过蓝桥真题的小伙伴应该都知道**DFS、BFS**的重要性，所以今天博主会通过两个小例题来带大家学习一下**DFS算法**，下期更新**BFS算法**，敬请期待！！

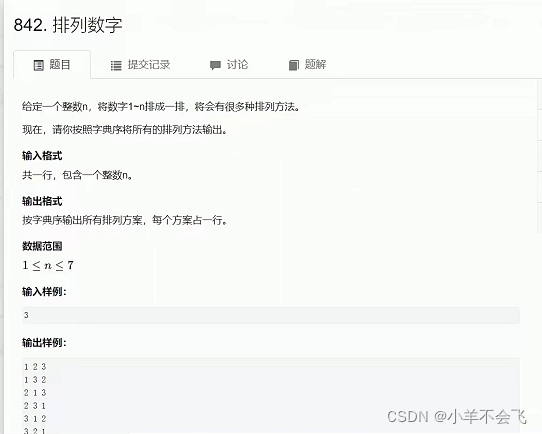
排列数字

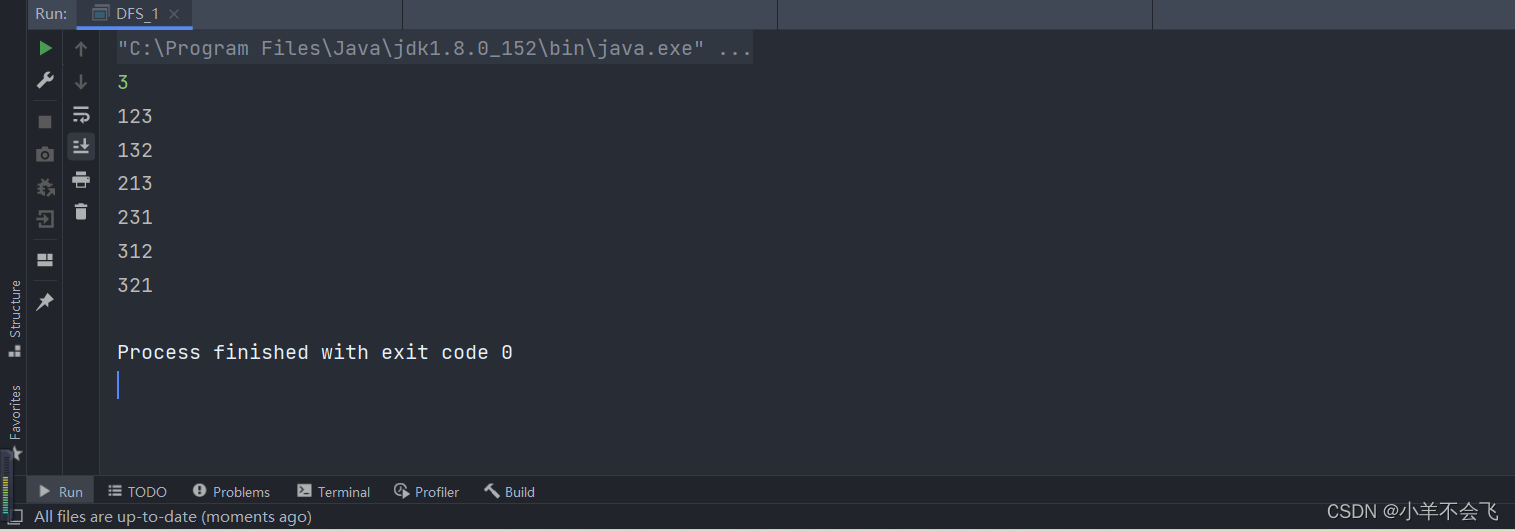
import java.util.Scanner;

/**
 * @author yx
 * @date 2022-01-29 14:23
 */
/*
排列数字问题
 */
public class DFS_1 {
    static boolean st[]=new boolean[10];//这两个数组是公用的所以要设置成静态的
    static int path[]=new int[10];

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n=scanner.nextInt();
        dfs(0,n);
        return;
    }
    static void dfs(int u,int n){
        if(u==n){//当遍历到最底部时，输出路径上所有的数
            for (int i=0;i<n;i++){
                System.out.print(path[i]);
            }
            System.out.println("");
            return;
        }
        //下面这段代码需要细细去理解
        for (int i=1;i<=n;i++){
            if(!st[i]){//刚开始赋值的时候默认st[i]为false
                path[u]=i;
                st[i]=true;
                dfs(u+1,n);
                st[i]=false;//回溯，恢复原节点
            }
        }
    }
}

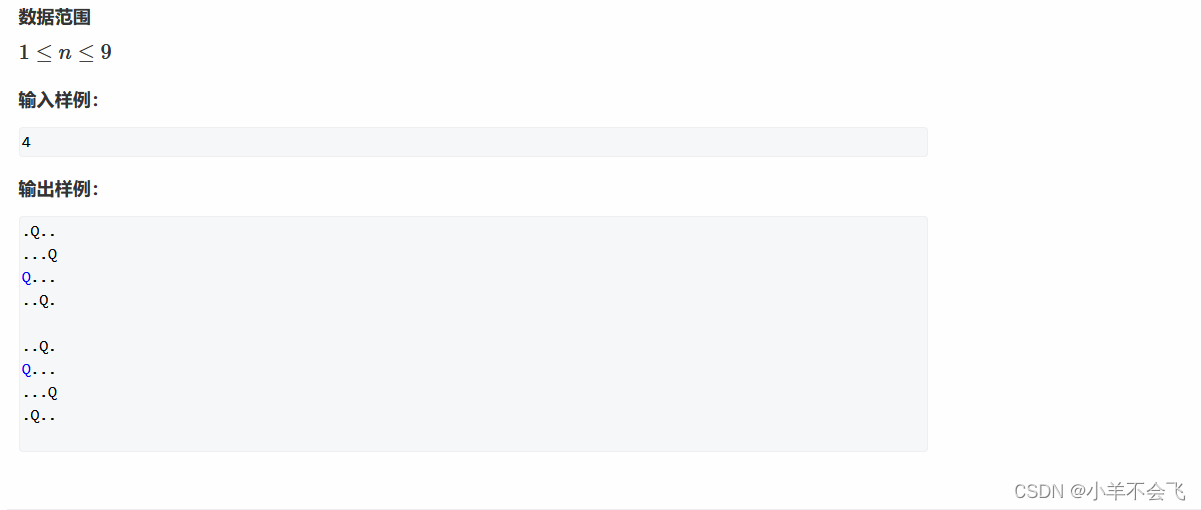
n-皇后问题

import java.util.Scanner;

/**
 * @author yx
 * @date 2022-01-29 23:11
 */
/*
八皇后问题
 */
public class DFS_2 {
    static char g[][]=new char[4][4];
    static boolean col[] = new boolean[20];
    static boolean dg[] = new boolean[20];//对角线数组
    static boolean udg[] = new boolean[20];//反对角线数组 

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n=scanner.nextInt();
        for (int i=0;i<n;i++){
            for (int j=0;j<n;j++){
                g[i][j]='.';
            }
        }
        dfs(0,n);
    }
    static void dfs(int u,int n){
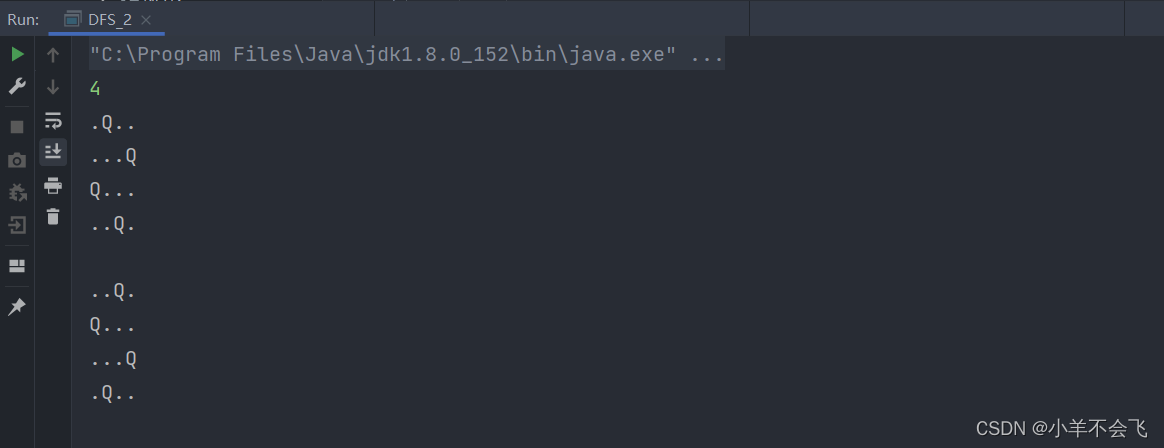
        if (u==n){
            for (int i=0;i<n;i++) System.out.println(g[i]);
            System.out.println("");
            return;
        }
        for (int i=0;i<n;i++){
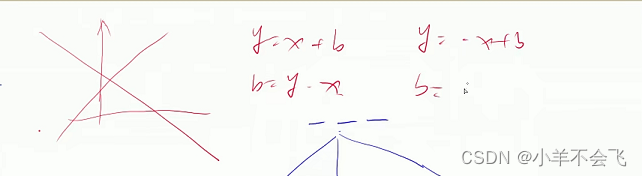
            if (!col[i]&&!dg[u+i]&&!udg[n-u+i]){//下标的原有如图解析所示
                g[u][i]='Q';
                col[i]=dg[u+i]=udg[n-u+i]=true;//表示（u，i）点的列、正斜对角线上被占用
                dfs(u+1,n);//递归
                col[i]=dg[u+i]=udg[n-u+i]=false;//回溯，回复原来的状态
                g[u][i]='.';
            }
        }
    }
}

dg[ u+i]、udg[n-u+i]内下标数字的解析

** 总结：**

** DFS的核心思想就是递归，上面这两个例子多花时间琢磨琢磨，静下心来感受算法的美。 **