人工智能学习框架—飞桨Paddle人工智能

1.人工智能框架

机器学习的三要素：模型、学习策略、优化算法。

当我们用机器学习来解决一些模式识别任务时，一般的流程包含以下几个步骤：

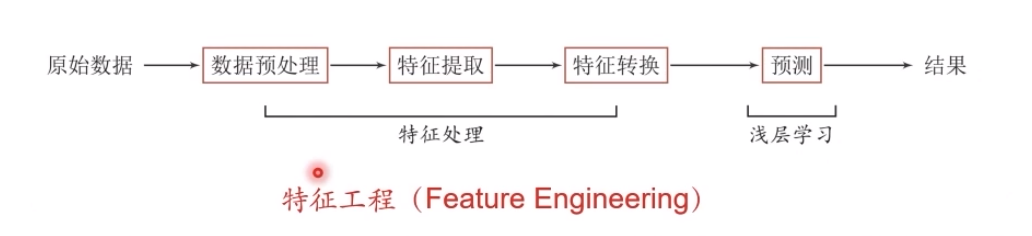
uTools_1691925173170

1.1.浅层学习和深度学习

浅层学习(Shallow Learning)：不涉及特征学习，其特征主要靠人工经验或特征转换方法来抽取。

底层特征VS高层语义：人们对文本、图像的理解无法从字符串或者图像的底层特征直接获得

深度学习通过构建具有一定“深度”的模型，可以让模型来自动学习好的特征表示（从底层特征，到中层特征，再到高层特征)，从而最终提升预测或识别的准确性。

uTools_1691925398973

深度学习的数学描述：

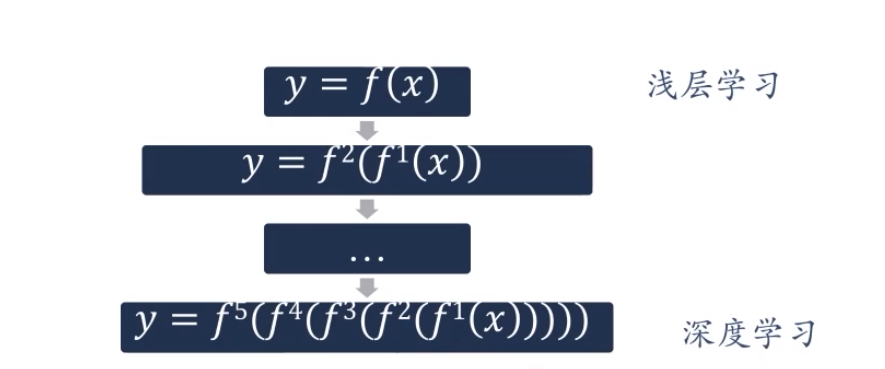
uTools_1691925529241

fl(x)为非线性函数，不一定连续。

深度学习的难点：

y=f^5^(f^4^(f^3^(f^2^(f^1^(x)))))

贡献度分配问题：一个复杂系统中每个组件对最终评价的贡献。

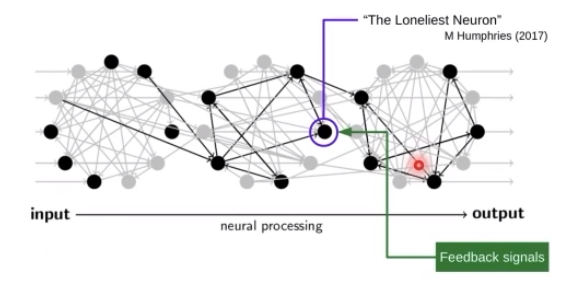
uTools_1691925707504

如何解决贡献度分配问题：

其中我们一般采用的方法就是求偏导数，也就是使用误差反向传播算法，这是我们学习神经网络的时候接触到过的。

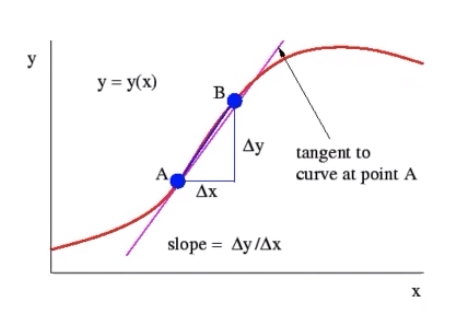
贡献度：

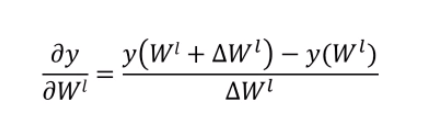
uTools_1691926340292

我们要知道一点，那就是神经网络天然不是深度学习，但深度学习天然是神经网络！

1.2.神经网络与深度学习的关系

人工智能的一个子领域

神经网络：一种以（人工）神经元为基本单元的模型

深度学习：一类机器学习问题，主要解决贡献度分配问题

uTools_1691926405209

我们都明白，机器（深度）学习非常有可能成为计算机学科的关键技术。

机器学习必然会发展到深度学习，不一定是神经网络，基于不可微架构的深度学习可能是未来方向。对于计算机学科是如此，而对于其他学科也是联系十分的紧密，深度学习也越来越多地成为传统学科的关键技术，涉及到数学、物理、化学、医药、天文、地理。

经过两周腾讯比赛，我对深度学习和强化学习有了自己的感悟：

理论支撑不足
调参一头雾水
模型无法解释
改进没有方向

当然，也有玩笑的成分在里面，也算是我和人工智能的第一次接触下来的感慨吧，领域多、知识点多，理论和实践紧密结合。

面对这些问题我们该怎么做嘞？

没错，就是肝各种前置知识，当然并行一起也可以。数学方面，就是线性代数、微积分、变分法、概率论、优化以及信息论。

我们需要在学习中逐步形成下面这张图的知识体系：

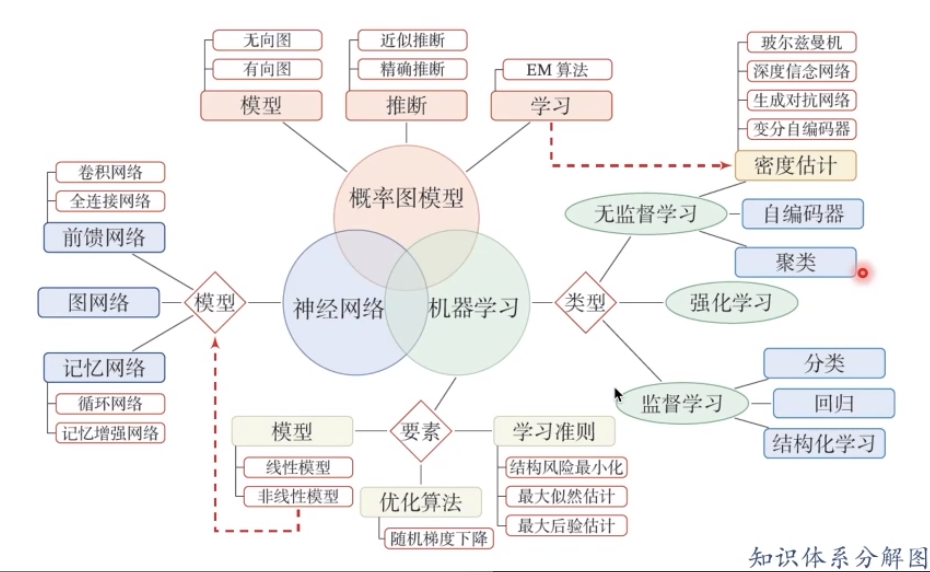
uTools_1691928991675

机器学习实践流程中的五要素：

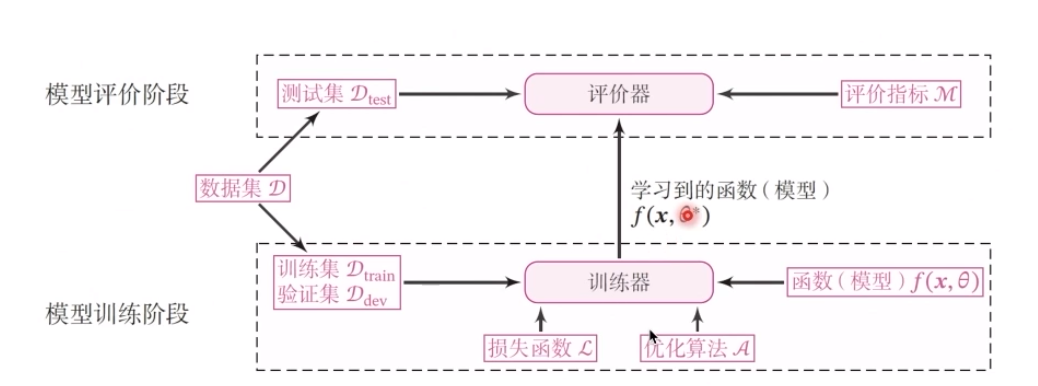
uTools_1691929291525

1.3.Runner类

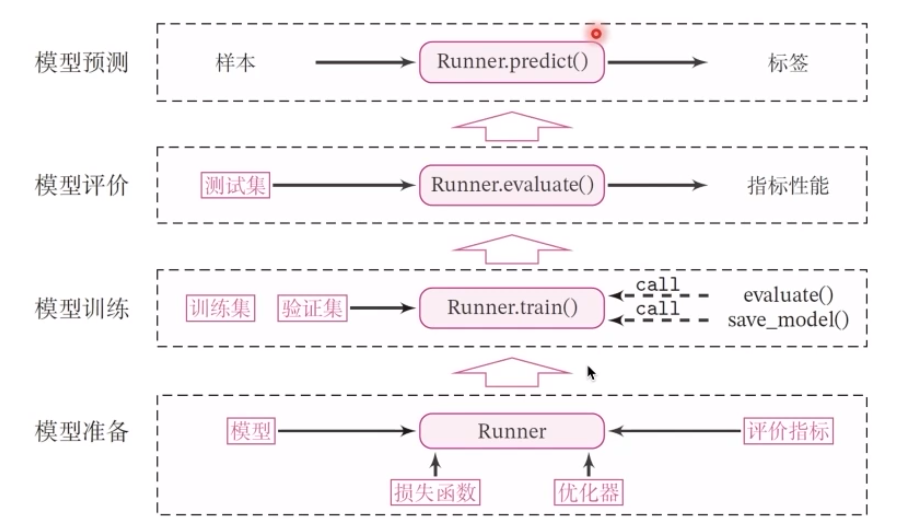
uTools_1691929456233

看到图上的箭头了吗，我们在模型准备中就是通过相应的损失函数、评价指标之后，也就是runner运行以后确定了模型合规，然后送到训练中，可能是强化训练进行探索，也可能是别的东西。像我们在腾讯开悟的比赛中，就是这样的形式，训练一定的时间就会出相应的模型，再提交到指定的平台进行模型评价和测试评估。

代码模板：

class Runner(object):
    def __init__(self, model, optimizer, loss_fn, metric):
        self.model = model #模型
        self.optimizer = optimizer #优化器
        self.1oss_fn = 1oss_fn #损失函数
        self.metric = metric #评价指标
        
    # 模型训练
    def train(self, train_dataset, dev_dataset=None, **kwargs):
        pass
    
    # 模型评价
    def evaluate(self, data_set, **kwargs):
        pass
    
    # 模型预测
    def predict(self, x, **kwargs):
        pass
    
    # 模型保存
    def save_model(self, save_path):
        pass
    
    # 模型加载
    def load_model(self, model_path):
        pass

1.4.张量与算子

数据的表现形式是张量

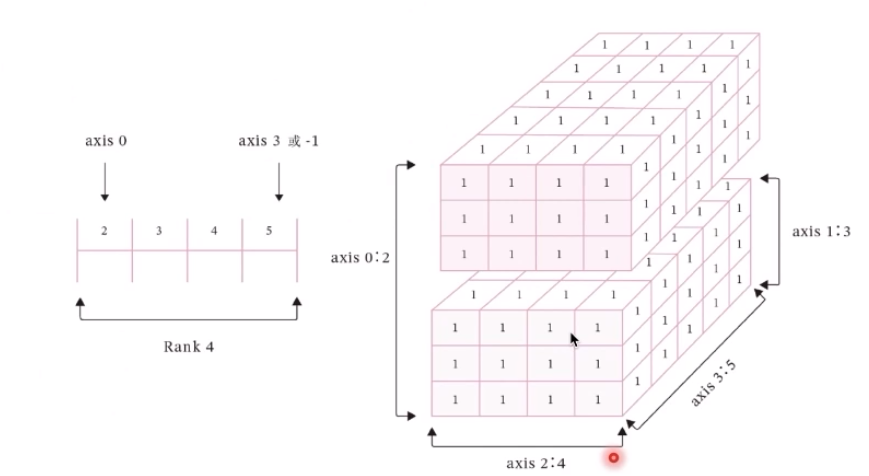
uTools_1691936884794

模型的基本单位：算子

class Op(object):
    def __init__(self):
        pass
    
    def __call__(self, inputs):
        return self.forward(inputs)
    
    # 前向函数
    # 输入：张量inputs
    # 输出：张量outputs
    def forward(self, inputs):
        # return outputs
        raise NotImplementedError
        
    # 反向函数
    # 输入：最终输出对outputs的梯度outputs_grads
    # 输出：最终输出对inputs的梯度inputs_grads
    def backward(self,outputs_grads):
        # return inputs_grads
        raise NotImplementedError

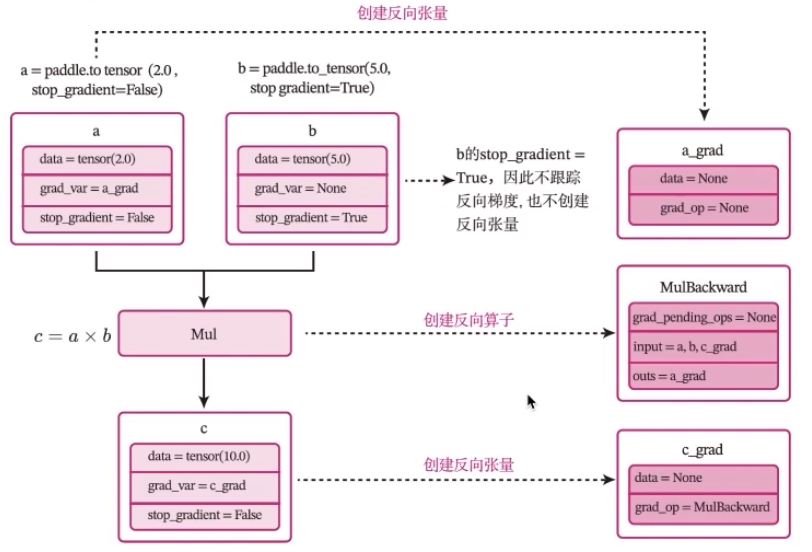
加法算子的前向和反向计算过程

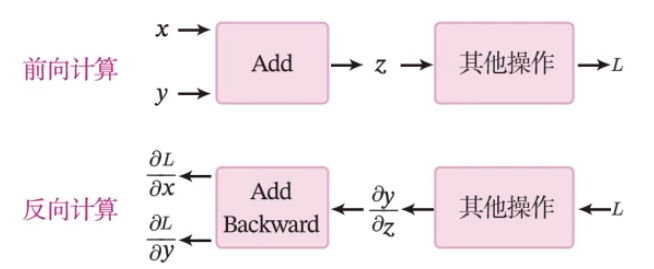
uTools_1691937846915

一个复杂的机器学习模型（比如神经网络）可以看做一个复合函数

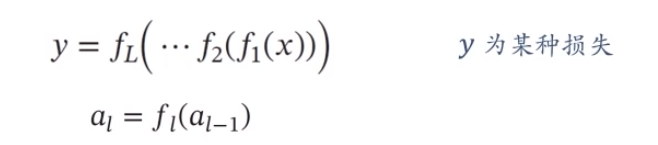
uTools_1691936991723

参数学习：梯度计算

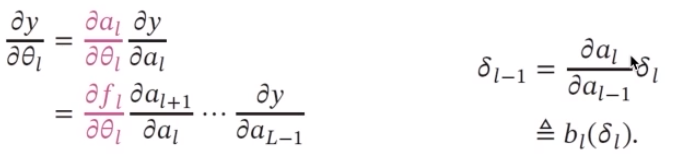
uTools_1691937058504

为了继承飞桨的

paddle.nn.layer

类

uTools_1691937923275

蒲公英一书中实现的Runner类：

RunnerV1

用于线性回归模型的训练，其中训练过程通过直接求解析解的方式得到模型参数，没有模型优化及计算损失函数过程，模型训练结束后保存模型参数

Runner V2

主要增加的功能为：①在训练过程中引入梯度下降法进行模型优化.

②在模型训练过程中计算训练集和验证集上的损失及评价指标并打印，在训练过程中保存最优模型

Runner V3

主要增加三个功能：使用随机梯度下降法进行参数优化.训练过程使用

DataLoader

加载批量数据.模型加载与保存中，模型参数使用

state_dict

方法获取，使用

state_dist

加载

Runner V3

基本上可以应用于大多数机器学习任务。

算子库nndl

从模型构建角度出发，借鉴深度学习框架中算子的概念，从基础开始一步步实现自定义的基本算子库，进一步通过组合自定义算子来搭建机器学习模型，最终搭建自己的机器学习模型库nndl。

在实践过程中不仅知其然还知其所以然，更好地掌握深度学习的模型和算法，并理解深度学习框架的实现原理。

2.NNDL开源库

NNDL (Neural Network Distillation Library) 是一个用于深度学习研究的开源库，主要用于知识蒸馏（Knowledge Distillation）任务。

知识蒸馏是一种将大型预训练模型（教师模型）的知识转移到小型模型（学生模型）的方法。NNDL 提供了一个框架，支持使用图像分类任务进行知识蒸馏，包括模型定义、训练和测试等过程。

该库主要特点包括：

支持多种流行的深度学习框架，如 TensorFlow 和 PyTorch。
提供多个预训练的教师模型，以及学生模型的蒸馏训练。
针对图像分类任务，支持各种数据增强和网络结构。
可用于开发高效的神经网络模型，包括卷积神经网络、循环神经网络等。

请注意，NNDL 是一个相对较新的开源库，可能存在一些限制和缺陷。在使用过程中，请确保您理解其工作原理和适用范围，并根据需要进行适当的调整和优化。

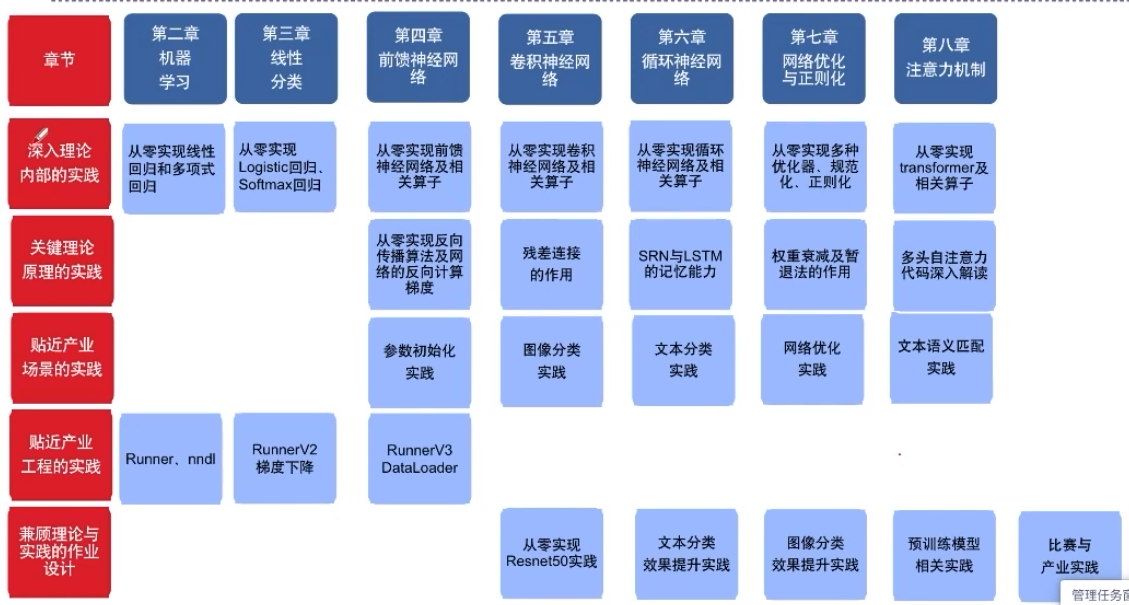
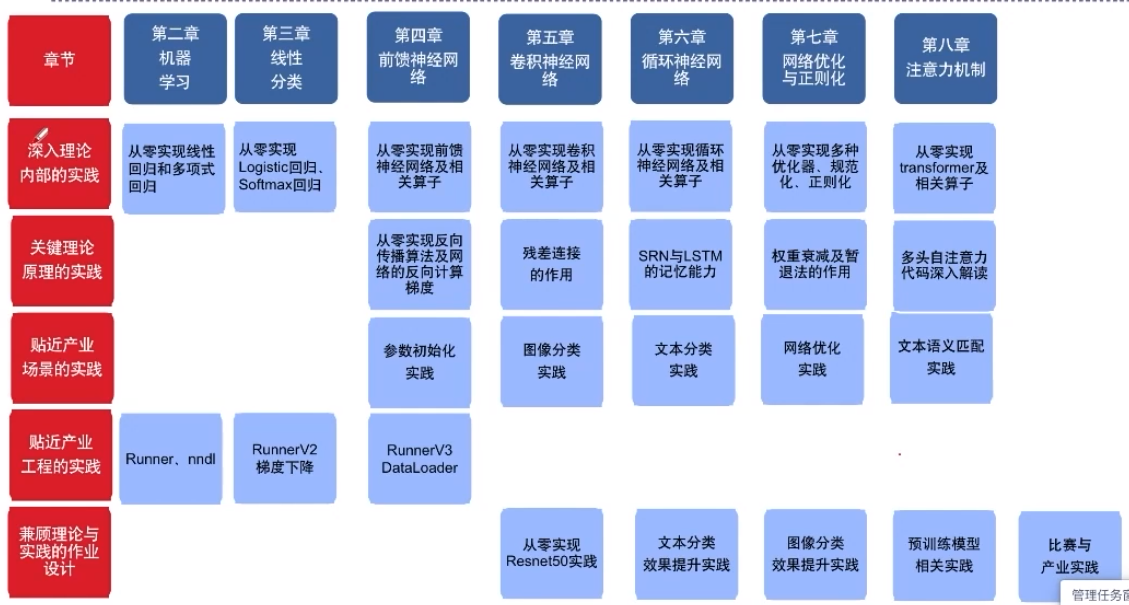
NNDL案例与实践的特色在于：

深入理论内部的实践，比如：从0实现反向传播、卷积、transformer等。
关键理论原理的实践，比如：SRN的记忆能力与梯度爆炸、LSTM的记忆能力等。
贴近产业场景的实践，比如：cnn实现图像分类、mn实现文本分类、transformer实现语义匹配等。
贴近产业工程的实践，比如：基于训练框架Runnert的实验、逐步完善的nnd工具包、模型精度速度的分析方法等。
兼顾理论与实践的作业设计，比如：基础知识回顾与实践，动手比赛和产业应用实践等。

uTools_1692010723000

3.模型训练

使用Runner，进行相关模型训练配置，即可启动模型训练

# 指定运行设备
use_gpu = True if paddle.get_device().startswith("gpu") else False
if use_gpu:
    paddle.set_device('gpu:0')
# 学习率大小
lr = 0.001
# 批次大小
batch_size = 64
# 加载数据
train_loader = io.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = io.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = io.DataLoader(test_dataset, batch_size=batch_size)
# 定义网络
model = resnet19_model
# 定义优化器，这里使用Adam优化器以及l2正则化策略，相关内容在后续会有相应的教程
optimizer = opt.Adam(learning_rate=lr, parameters=model.parameters(), weight_decay=0.005)
# 定义损失函数
loss_fn = F.cross_entropy
# 定义评价指标
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 启动训练
log_steps = 3000
eval_steps = 3000
runner.train(train_loader,dev_loader,num_epochs=30,log_steps=log_steps,
             eval_steps=eval_steps,save_path="best_model.pdparams")

4.残差网络

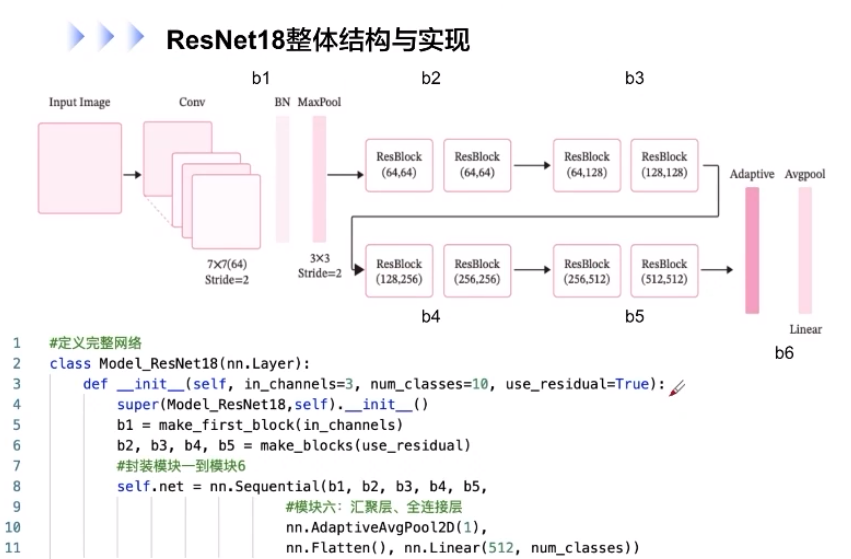
残差网络：在神经网络模型中给非线性层增加直连边的方式来缓解梯度消失问题，从而使训练深度神经网络变得更加容易
残差单元：一个典型的残差单元由多个级联的卷积层和一个跨层的直连边组成ResBlock f(x) = f(x; θ)+x
Transformer：加与规范层，H=LN(H+X)
Gradient Boosting：Greedy Function Approximation:A Gradient Boosting Machine，GBDT:Gradient Boosting Decision Tree

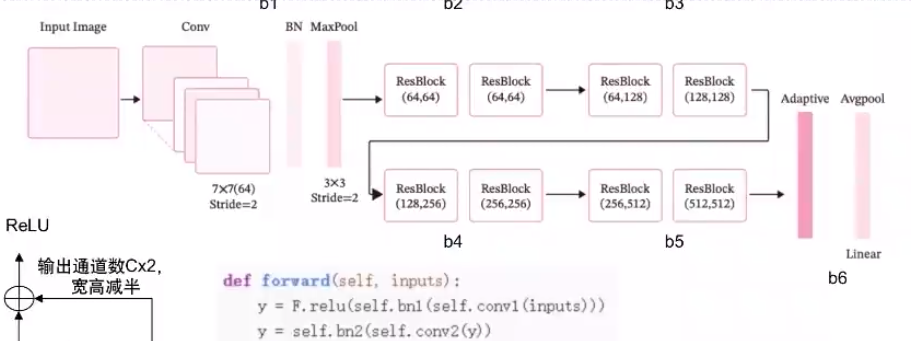
uTools_1692012181100

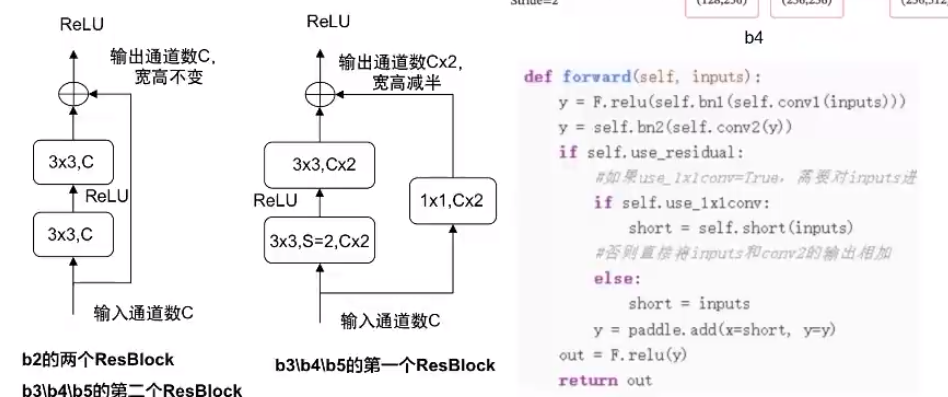
uTools_1692012202408

ResNet18整体结构与实现：

uTools_1692012728749

# 定义完整网络
class Model_ResNet18(nn.Layer):
    def __init__(self, in_channels=3, num_classes=10, use_residual=Ture):
        super(Model_ResNet18, self).__init__()
        b1 = make_first_block(in_channels)
        b2, b3, b4, b5 = make_blocks(use_residual)
        # 封装模板1到模板6
        self.net = nn.Sequential(b1, b2, b3, b4, b5,
                                # 模块6：汇聚层、全连接层
                                nn.AdaptiveAvgPool2D(1),
                                nn.Flatten(), nn.Linear(512, num_classes))

然后针对构建ResNet18中各模块，后序会有所介绍，这里就以b1为例，展示一下它相应的代码

def make_first_block(in_channels):
    # m模块1：7*7卷积、批归一化、汇聚
    b1 = nn.Sequential(nn.Conv2D(in_channels, 64, kernel_size=7, stride=2, padding=3),
                      nn.BatchNorm2D(64), nn.ReLU(),
                      nn.MaxPool2D(kernel_size=3, stride=2, padding=1))
    return b1

通常而言，特别是是在模型评价中，不带残差连接的ResNet18网络的准确率是远小于加了残差连接的神经网络的，模型效果差别是相当显著的。

5.卷积神经网络应用及原理

5.1.卷积神经网络

卷积一词我们并不陌生，我们在学习深度学习或者强化学习经常会遇到卷积这个概念。简而言之，卷积就是将我们的数据进行处理，处理得足够小，足以让我们的机器去识别。

在二维卷积算子中，我们的目的是在具体实现上，以互相运算来代替卷积，对于一个输入矩阵X∈RMN，使用滤波器W∈RUV进行运算。

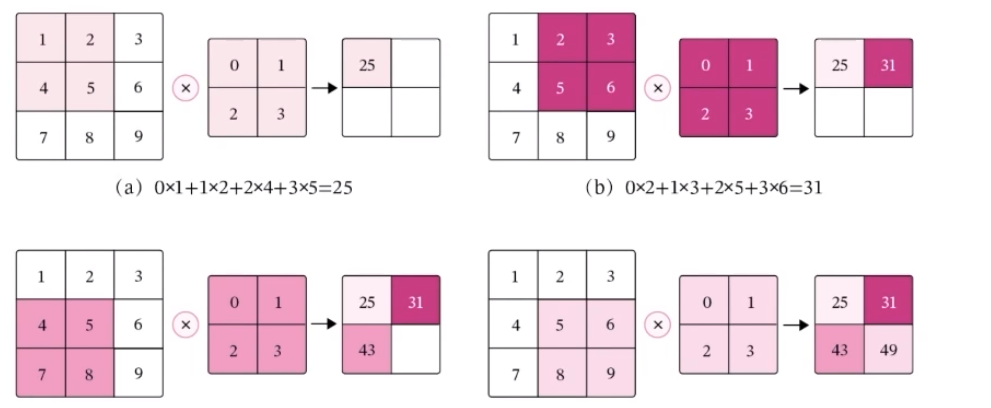
uTools_1692013957228

上面的深色区域也就是我们所说的滑动窗口（嘿嘿，情不自禁想起了y总算法基础课里的滑动窗口一题，那个是一个典型的动态规划问题），为了实现局部信息到全局信息的融合，通过权值共享实现了参数量的不增加，降低了网络模型的复杂度，减少了权值的数目。参数的。在整个网络的训练过程中，包含权值的卷积核也会随之更新，直到训练完成。

输出特征图大小：

M' = M - U + 1

N' = N - V + 1

特性：

局部连接：第i层中的每一个神经元都只和第i-1层中某个局部窗口内的神经元相连，构成一个局部连接网络。
权重共享：所有作为参数的卷积核W∈RU*V对于第i层的所有神经元都是相同的。

二维卷积算子：

可以随机构造一个二维输入矩阵

paddle.seed(100)
inputs = paddle.to_tensor([[[1.,2.,3.],[4.,5.,6.],[7.,8.,9.]]])

conv2d = Conv2D(kernel_size=2)
outputs = conv2d(inputs)
print("input:{}\noutput:{}"format(inputs,outputs))

5.2.API说明

API（Application Programming Interface，应用程序编程接口）是一种定义软件组件之间如何通信的规范。它提供了一种标准化的接口，允许不同的软件系统之间进行交互和通信。

API通常是一组预先定义的函数、方法、类和对象，开发人员可以使用这些接口来调用软件组件的功能。API还规定了如何传递参数、返回值以及错误处理等细节。

API说明通常包括以下内容：

接口名称和功能描述：提供接口的名称和功能描述，让开发人员了解该接口的作用和用途。
输入参数说明：详细说明每个输入参数的名称、类型、意义和用法，以确保开发人员正确地使用这些参数。
返回值说明：解释每个返回值的含义和用法，以及在成功或失败时返回什么样的数据。
错误处理说明：描述可能会出现的错误和异常情况，并提供相应的处理方法。
其他注意事项：提供其他与接口相关的信息和注意事项，例如使用限制、安全要求等。

通过阅读API说明，开发人员可以更好地理解接口的用途和使用方法，从而更有效地使用API进行软件开发和集成。

paddle.create_parameter(shape,dtype,attr=None)

功能：创建一个可学习的

Parameter

变量

输入：

Parameter

变量的形状、数据类型、属性

输出：创建的Parameter变量

二维卷积算子的参数量

对于一个输入矩阵X∈RMxN，使用滤波器W∈RUxV进行运算，卷积核的参数量为：U×V

假设有一个32×32大小的图像，使用隐藏层神经元个数为1的全连接前馈网络进行处理：

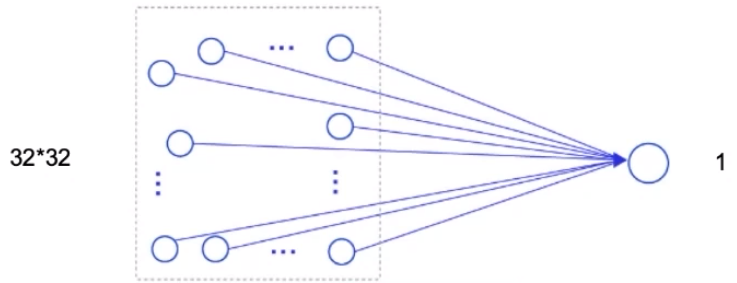
uTools_1692017872092

32 * 32 + 1 =1025

使用3 * 3卷积核进行处理，参数量为：9

5.3.二维卷积算子的计算量

计算量：网络乘加运算总次数

FLOPs=M' * N' * U * V

假设有一个32×32大小的图像，使用3×3卷积核进行处理，计算量为：

M' = M - U + 1 = 30

N' = N - V + 1 = 30

FL0Ps = M' × N' × U × V = 30 × 30 × 3 × 3 = 8100

5.4.感受野

这个概念也不陌生，是指神经元或感受器能接受刺激的空间范围。在视觉系统中，它通常指的是视网膜上一个简单的、没有特定方向性的感受器（即非方向性光感受器）能接收到的空间范围。在中枢中，某一神经元的感受野是分布于其胞体和树突上，是在时间和空间上能被神经元响应的各种形式的光刺激模式（即特定的空间频率特性）的总和。

就如下面两个特征图：

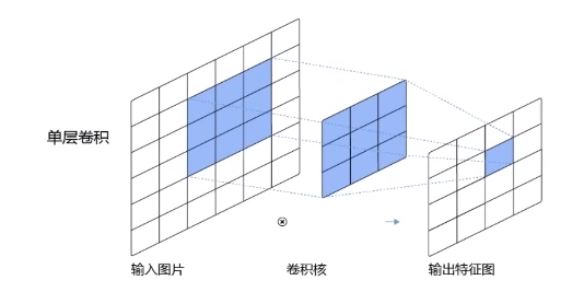
uTools_1692018794565

感受野大小：3 x 3

输出特征图上的像素点所能感受到的输入数据的范围

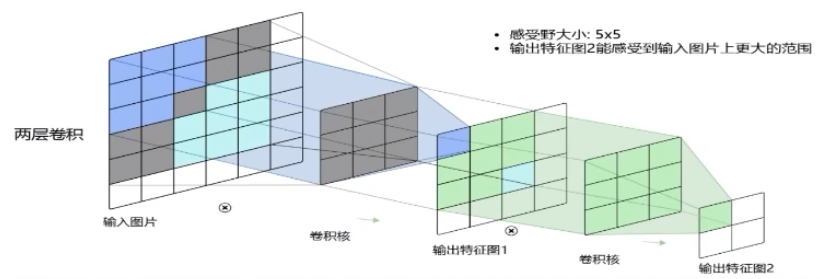
uTools_1692018861836

5.5.带步长和零填充的二维卷积算子

步长(Stride)

在所有维度上每隔S个元素计算一次，S称为卷积的步长

对于一个输入矩阵X∈RMxW，使用滤波器W∈RUxV进行运算

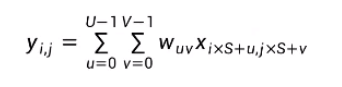
uTools_1692020011940

零填充（Zero Padding)

如果不进行填充，当卷积核尺寸大于时，输出特征会缩减

对输入进行零填充可以对卷积核的宽度和输出的大小进行独立的控制

对于一个输入矩阵X∈RMxN，使用滤波器W∈RUxV进行运算，步长为S，并进行零填充后，输出矩阵大小为：

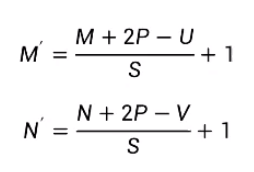
uTools_1692020088081

参数量：U x V

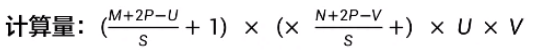
uTools_1692020121840

带步长和零填充的二维卷积算子代码

class Conv2D(nn.Layer):
    def __init__(self, kernel_size, stride=1, padding=0,
                 weight_attr=paddle.ParamAttr(initializer=nn.initializer.Constant(value=1.0))):
        super(Conv2D, self).__init__()
        self.weight = paddle.create_parameter(shape=[kernel_size,kernel_size],
                                             dtype='float32',
                                             attr=weight_attr)
        # 步长
        self.stride = stride
        # 零填充
        self.padding = padding
        
    def forward(self, X):
        # 零填充
        new_X = paddle.zeros([X.shape[0], X.shape[1]+2*self.padding, X.shape[2]+2*self.padding])
        new_X[:, self.padding:X.shape[1]+self.padding, self.padding:X.shape[2]+self.padding] = X
        u, v = self.weight.shape
        output_w = (new_X.shap[1] - u) // self.stride + 1
        output_h = (new_X.shap[2] - u) // self.stride + 1
        output = paddle.zeros([X.shape[0], output_w, output_h])
        for i in range(0, output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = paddle.sum(
                new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*self.weight,
                axis=[1,2])
                return output
            
inputs = paddle.randn(shape=[2, 8, 8])
conv2d_padding = Conv2D(kernel_size=3, padding=1)
outputs = conv2d_padding(inputs)
print("When kernel_size=3,padding=1 stride=1,input's shape:{}output's shape:()"format(inputs.shape,outputs.shape))
conv2d_stride Conv2D(kernel_size=3,stride=2,padding=1)
outputs conv2d_stride(inputs)

卷积神经网络

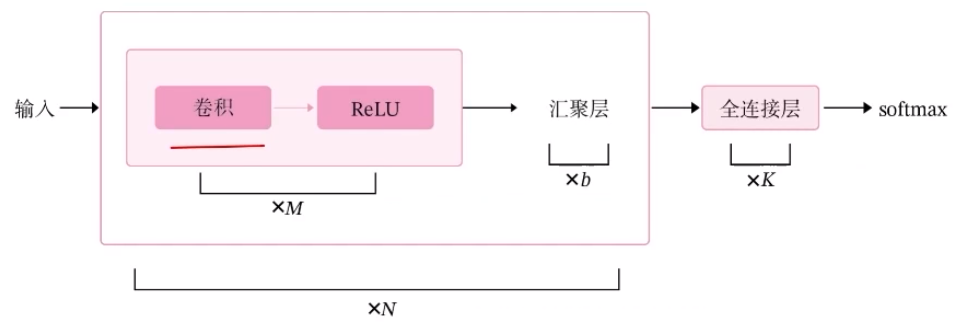
uTools_1692026218401

6.卷积层算子

输入通道：等于输入特征图的深度D

例如：输入是灰度图像，则输入通道数为1；输入是彩色图像，分别有R、G、B三个通道，则输入通道数为3；输入是深度D的特征图，则输入通道数为D

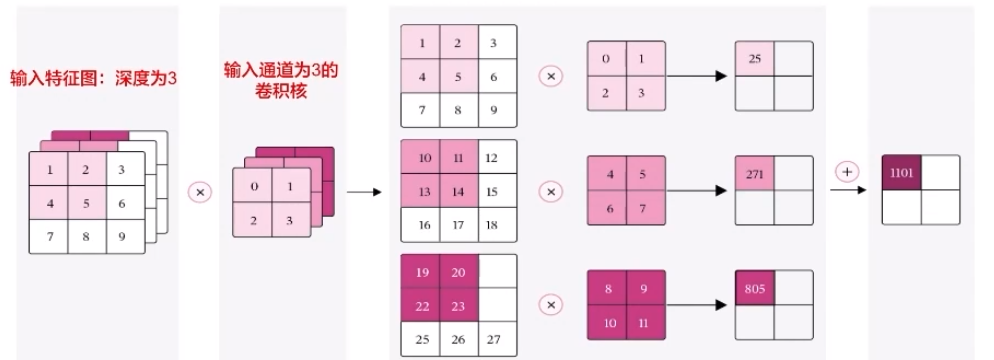
uTools_1692026260543

6.1.多通道卷积层算子

class Conv2D(nn.Layer):
    def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0,
                weight_attr=paddle.ParamAttr(initializer=nn.initializer.Constant(value=1.0)),
                bias_attr=paddle.ParamAttr(initializer.Constant(value=0.0))):
        super(Conv2D, self).__init__()
        #创建卷积核
        self.weight = paddle.create_parameter(shape=[out_channels, in_channels, kernel_size, kernel_size],
                                              dtype='float32',
                                              attr=weight_attr)
        #创建偏置
        self.bias = paddle.create_parameter(shape=[out_channels, 1],
                                            dtype='float32',
                                            attr=bias_attr)
        self.stride = stride
        self.padding = padding
        #输入通道数
        self.in_channels = in_channels
        #输出通道数
        self.out_channels = out_channels
    #基础卷积运算
    def single_forward(self, X, weight):
        #零填充
        new_X = paddle.zeros([X.shape[0],X.shape[1]+2*self.padding,X.shape[2]+2*self.padding])
        new_X[:,self.padding:X.shape[1]+self.padding,self.padding:X.shape[2]+self.padding]=x
        u,v weight.shape
        output_w =(new_X.shape[1]u)//self.stride +1
        output_h (new_X.shape[2]-v)//self.stride 1
        output paddle.zeros([X.shape[e],output_w,output_h])
        for i in range(0,output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = paddle.sum(
                new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*self.weight,
                axis=[1,2])
                return output

6.2.汇聚层算子

平均汇聚：将输入特征图划分多个为M'×N'大小的区域，对每个区域内的神经元活性值取平均值作为这个区域的表示

最大汇聚：使用输入特征图的每个子区域内所有神经元的最大活性值作为这个区域的表示

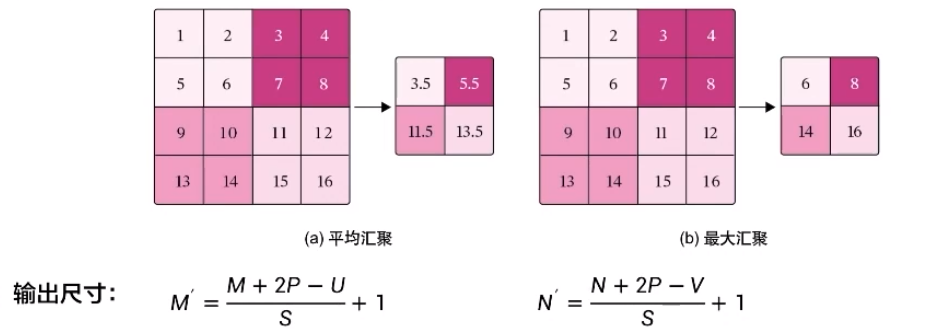
uTools_1692107743509

平移不变：当输入数据做出少量平移时，经过汇聚运算后的大多数输出还能保持不变。

参数量：0 计算量：最大汇聚为0 平均汇聚为

M' x N' x P

6.3.双向LSTM和注意力机制的文本分类-注意力层

嵌入层：将输入句子中的词语转换成向量表示；

LSTM层：基于双向LSTM网络来构建句子中的上下文表示；

注意力层：使用注意力机制从LSTM的输出中筛选和聚合有效特征；

线性层：输出层，预测对应的类别得分。

6.4.注意力机制

从N个输入向量中选择出和某个特定任务相关的信息。

输入向量：

X=[x1;...;Xn]

小，其中

Xn

是向量，X∈RNxD其中n是序列长度，D表示每个元素的维度

查询向量：q，任务相关

uTools_1692111100737

打分函数

加强模型，双线性模型

点积模型，缩放点积模型

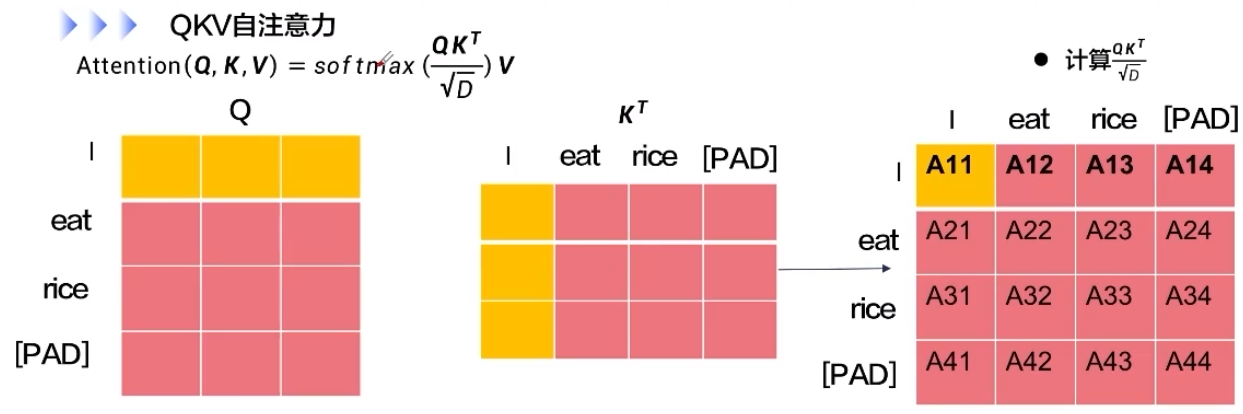
QKV自注意力的深度代码解读

uTools_1692111844835

标签：学习 linux windows

本文转载自: https://blog.csdn.net/Williamtym/article/details/128302652
版权归原作者 Williamtym 所有，如有侵权，请联系我们删除。