0
0

【C++】一篇了解AVL实现细节（易懂图解版）

文章目录

AVL是啥

AVL是一颗高度平衡的搜索二叉树，每颗子树的左右高度差不超过1，这种结构实际上是为了方便查找而设计的，由于普通的二叉搜索树在一些特定的情况会变成单叉树，此时就会成为一个单链表，单链表的查找就是O（N）了，所以AVL的设计是想通过插入和删除的麻烦来铸造一个查找方便的容器。

AVL树的所有操作时间复杂度都是O（logN）

开始学习！！

AVL节点定义

节点定义：我们通过三叉链配合_bf（平衡因子）实现，所谓的平衡因子就是检测树是否已经不高度平衡的一个依据。

template<classK>structTreeNode{TreeNode(const K& val):_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0),_val(val){}//三叉链
    TreeNode<K>* _left;// 左节点
    TreeNode<K>* _right;//右节点
    TreeNode<K>* _parent;//父节点int _bf;// 平衡因子
    K _val;// 节点的值};

节点插入

平衡因子更新的情况：当插入新的节点的时候，该节点的父节点的平衡因子会发生变化，若插入在父节点的右树，父节点平衡因子加加，若插入在父节点的左侧，父节点的平衡因子减减。

  • 1.当父节点的平衡因子为1/-1时，说明在此期间这颗父节点所在的子树的高度发生了变化，而这种变化可能会影响上一层，所以要向上更新。
  • 2.若父节点的平衡因子为0，为0则说明新增加的节点填补了子树本来矮的那一边，并不影响子树的高度，也就不用更新上一层了。
  • 3.若平衡因子为2/-2，说明该子树的左右高度差超过了1，需要进行翻转，翻转过后无需往父节点更新了。

单旋的情况分为四种：左单旋，右单旋，左右双旋，右左双旋。

左单旋

同理，但在60的右子树插入节点的时候，若跟新到30平衡因子为2后，若60的平衡因子为1时，此时需要左单旋。
左单旋总结：
1.改变两个左右指针，改变三个父指针，考虑b存不存在的情况，考虑30为根节点的情况，改变30和60的平衡因子。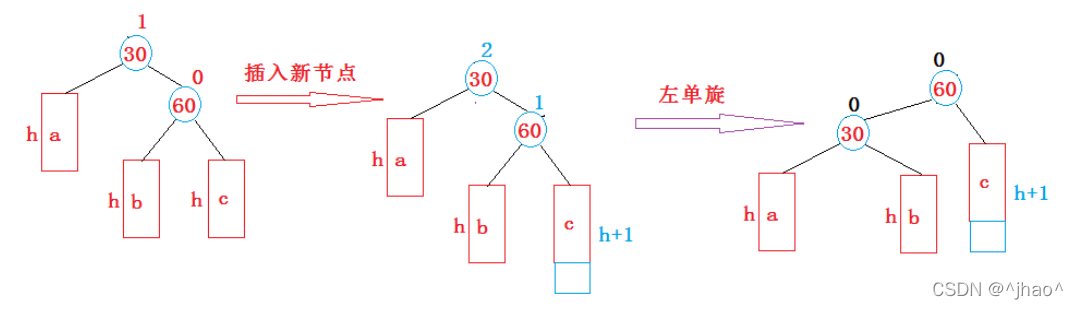
在这里插入图片描述
具体情况分析{1，2，3}：
当3是新插入节点，需要更改的节点有1的父亲节点（1可能不是根，需要特判）的右指针，1的父节点以及右节点的指向，2的父节点的指向，2的左节点的指向。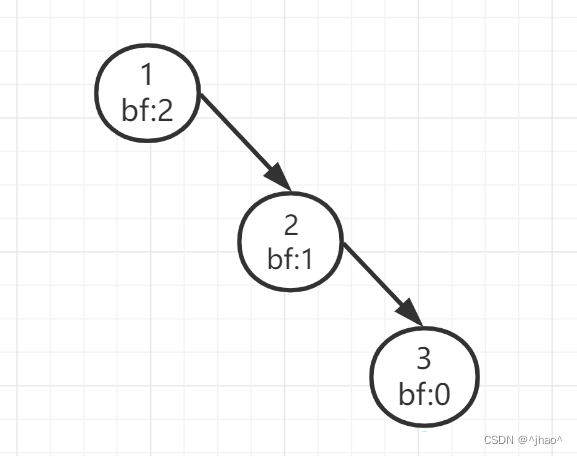
在这里插入图片描述
复杂情况分析：
此时需要更改的节点除了上面的除外，还有1.5的父节点需要指向1，这个很容易被忽略。
并且插入的节点在3的左侧和右侧对于翻转而言没有太大区别，而在左右双旋则有区别。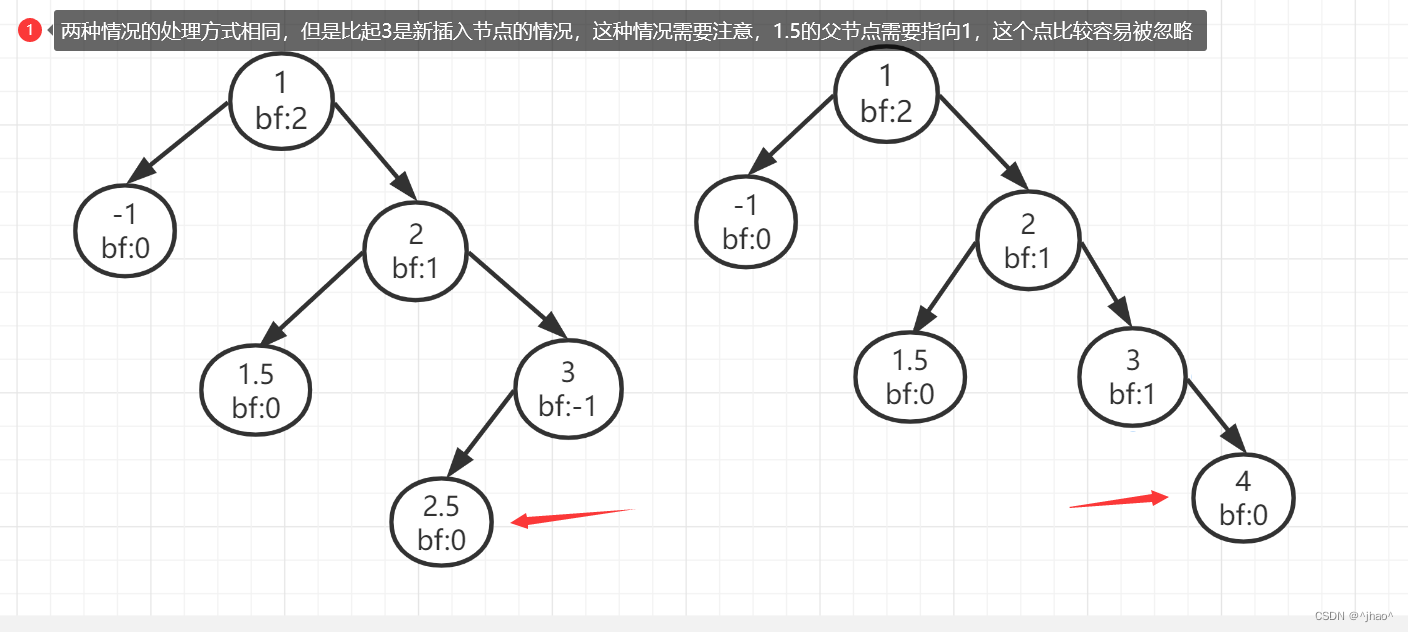
在这里插入图片描述

voidRotateL(Node* father){
        Node* subR = father->_right;
        Node* subRL = subR->_left;//两个左右指针
        father->_right = subRL;
        subR->_left = father;

        Node* ppNode = father->_parent;//处理三个父指针if(subRL){
            subRL->_parent = father;}
        father->_parent = subR;//父亲跟新到头节点的情况if(father == _root){
            _root = subR;
            subR->_parent =nullptr;}else{//ppNode结构体的指针指向没有改变if(ppNode->_left == father){
                ppNode->_left = subR;
                subR->_parent = ppNode;}else{
                ppNode->_right = subR;
                subR->_parent = ppNode;}}//处理平衡因子，只有father和subR的子树发生了变化
        father->_bf = subR->_bf =0;}

右单旋

当30的左子树插入了一颗节点，不管插入在30的左子树的哪个部分，都会导致30的平衡因子变成-1，所以需要往60跟新，60跟新后平衡因子为-2，需要进行翻转。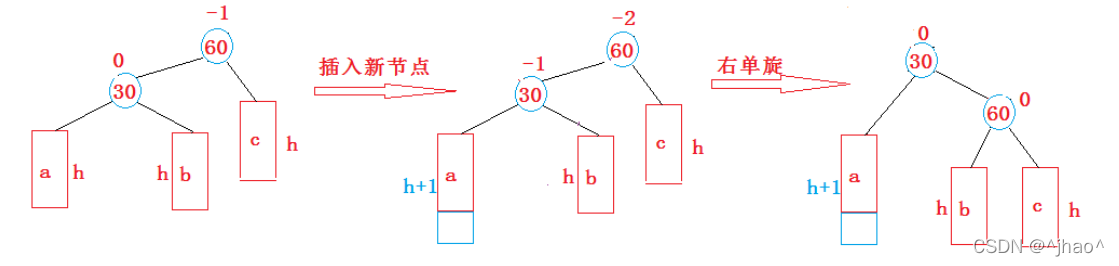
在这里插入图片描述
右单选分析：
60的左子树相当于高于60的右子树，所以需要右旋转，因为30的平衡因子为-1，此时需要进行右单旋。即60要充当30的右子树，所以提前将30的右子树插入到60的左子树，30的右子树再链接60。旋转完成过后由于60，30的左右子树发生了变化，所以只有他们的平衡因子需要发生变化，即右单旋需要将他们的平衡因子改变为0，并且由于是三叉链，需要对b树的父亲指针和60，30的父亲指针进行变化。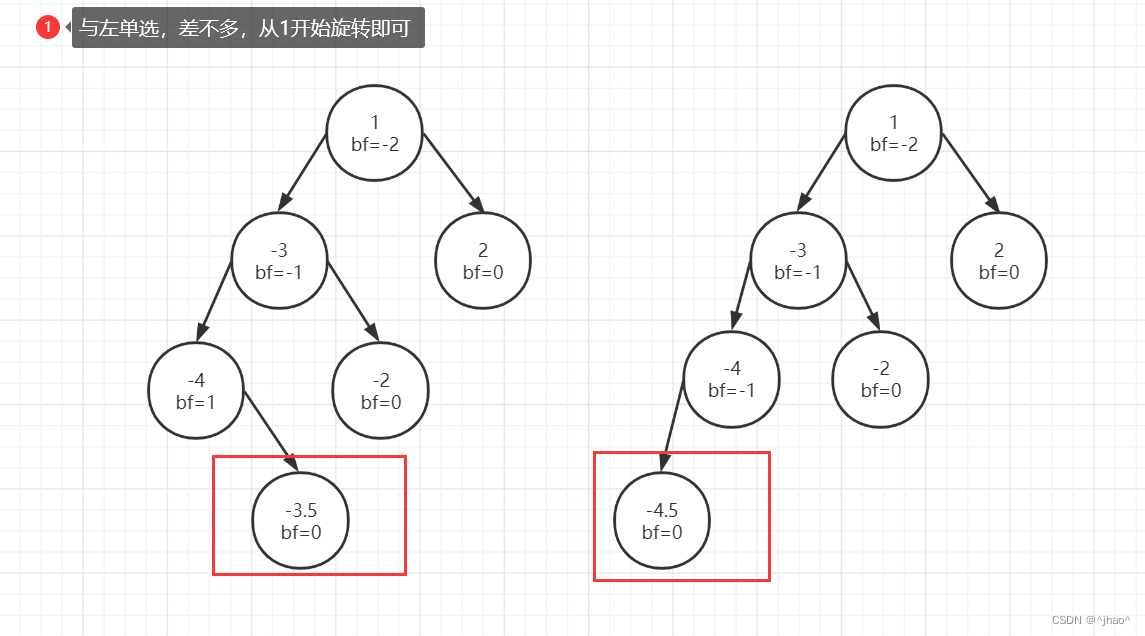
在这里插入图片描述

右单选总结：两个左右指针的变化，三个父亲节点的变化，还需要考虑父亲是根的情况。特判h==0时，b树不存在则不需要更改父亲节点。

//father为上述过程的60，subL即30，subLR即b子树voidRotateR(Node* father){
        Node* subL = father->_left;
        Node* subLR = subL->_right;
        Node* ppNode = father->_parent;//两个左右指针
        father->_left = subLR;
        subL->_right = father;//三个头指针if(subLR){
            subLR->_parent = father;}
        father->_parent = subL;
        subL->_parent = ppNode;//ppNode为NULL或其他都可以if(father == _root){
            _root = subL;}else{if(ppNode->_left == father){
                ppNode->_left = subL;}else{
                ppNode->_right = subL;}}
        subL->_bf = father->_bf =0;}

难点来咯~~

左右单旋

考虑的情况：60为新插入的节点（h==0的情况）
若60为新增节点，则左右单旋后的90，30，60的平衡因子均为0，改变30，60，90的父节点，再设置60为新增节点即可。

若在60的左或右子树插入则只有最后30，60，90的平衡因子有差异而已，都是先以30为父节点左旋，再以90为父节点右旋。
情况2：往60的左子树插入
在这里插入图片描述
情况3：往60的右子树插入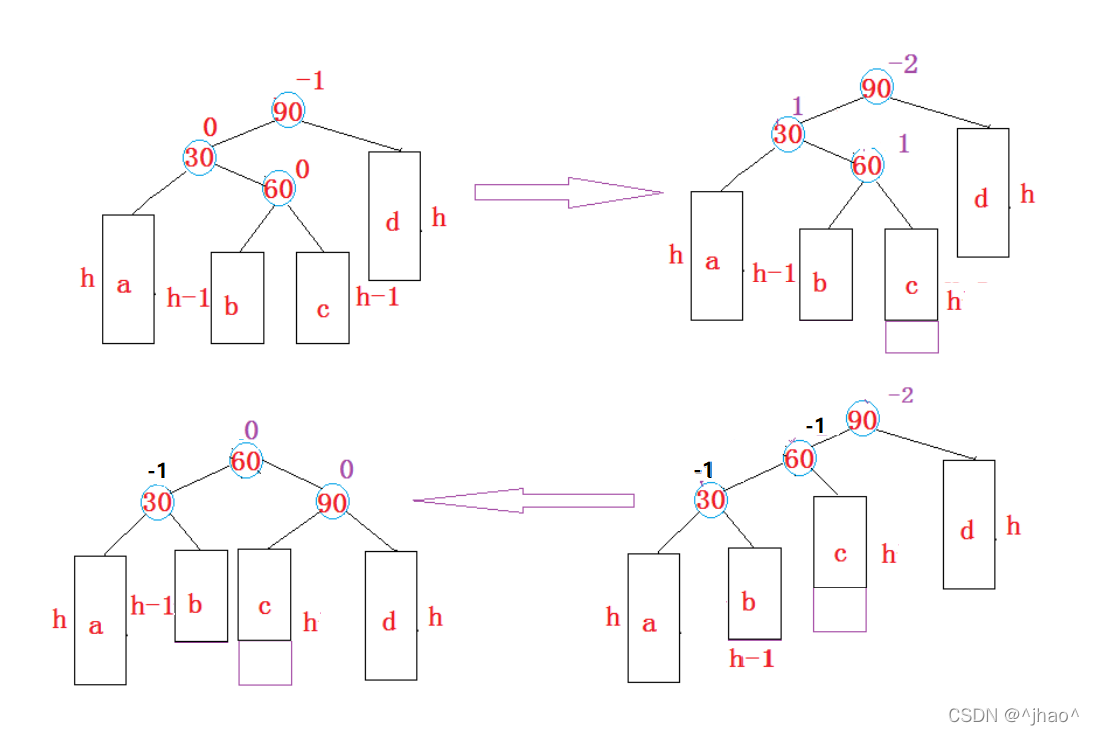在这里插入图片描述

voidRotateLR(Node* parent){
        Node* subL = parent->_left;
        Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);//三种情况的平衡因子需要跟新//关键看subLR的平衡因子，确定插入节点是它本身还是左右//只影响三个节点左右节点，所以只有他们的高度差会变if(bf ==0){
            subLR->_bf = subLR->_bf = parent->_bf =0;}elseif(bf ==1){/*parent->_bf = -1;
            subLR->_bf = subL->_bf = 0;*/
            parent->_bf = subLR->_bf =0;
            subL->_bf =-1;}elseif(bf ==-1){/*subL->_bf = 1;
            subLR->_bf = parent->_bf = 0;*/
            subL->_bf = subLR->_bf =0;
            parent->_bf =1;}else{assert(false);}}

同理右左双旋(配合图片编写代码最佳)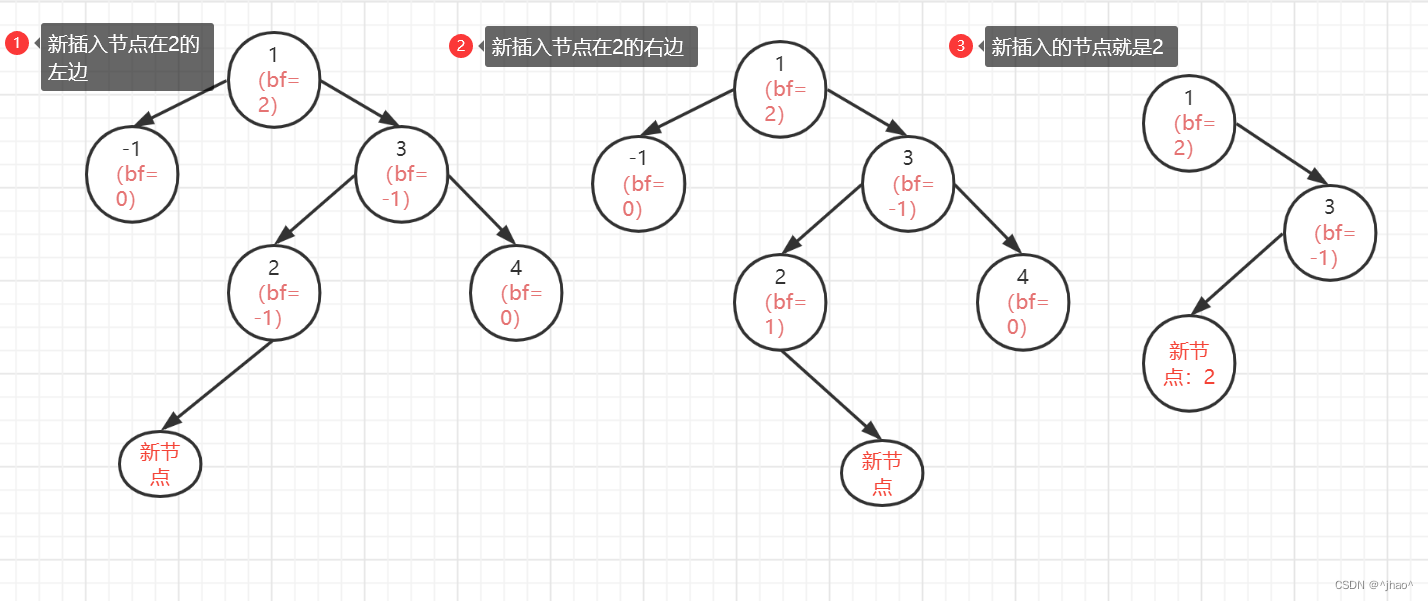
在这里插入图片描述

voidRotateRL(Node* parent){
        Node* subR = parent->_right;
        Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if(bf ==0){
            subR->_bf = subRL->_bf = parent->_bf =0;}elseif(bf ==-1){/*parent->_bf = 1;
            subRL->_bf = subR->_bf = 0;*/
            parent->_bf = subRL->_bf =0;
            subR->_bf =1;}elseif(bf ==1){/*subR->_bf = -1;
            parent->_bf = subRL->_bf = 0;*/
            parent->_bf =-1;
            subRL->_bf = subR->_bf =0;}else{assert(false);}}

判断是否为AVL树

intHeight(Node* node){if(node ==nullptr)return0;return std::max(Height(node->_left),Height(node->_right))+1;}bool_is_avl(Node* root){if(root ==nullptr)returntrue;int leftHeight =Height(root->_left);int rightHeight =Height(root->_right);if(rightHeight - leftHeight != root->_bf){
                cout <<"平衡因子错误:"<<root->_val<<" "<< root->_bf <<" "<< rightHeight - leftHeight << endl;}returnabs(leftHeight - rightHeight)<2&&_is_avl(root->_left)&&_is_avl(root->_right);}

注意：

  • 旋转过后，影响到的节点，bf==2的节点以及其父亲节点，及其左/右节点，以及其左右/右左节点（若不为空）都会受到影响。
  • 在左右双旋和右左双旋的情况当中，当在叶子节点插入的位置不同，会造成三种情况，其中可以使用左右双旋的基础上各自在每个节点空闲处添加节点得到不同的测试用例。
  • 三种情况导致的最后的平衡因子都不相同，所以需要注意。

实现代码

实现的注意细节：
在找到空姐点的时候，父节点连接时需要通过节点值进行比较，不能直接通过节点进行比较，

因为父节点的左右节点可能都为空

编码：
这个实现变量的定义有些不同，但是实现还是按照上面相似的。

AVLTree.hpp

#pragmaonce#include<iostream>#include<stack>#include<queue>#include<assert.h>using std::queue;using std::stack;template<classT>structAVLTreeNode{AVLTreeNode(const T& data =T()):_pLeft(nullptr),_pRight(nullptr),_pParent(nullptr),_data(data),_bf(0){}

    AVLTreeNode<T>* _pLeft;
    AVLTreeNode<T>* _pRight;
    AVLTreeNode<T>* _pParent;
    T _data;int _bf;// 节点的平衡因子};// AVL: 二叉搜索树 + 平衡因子的限制template<classT>classAVLTree{typedef AVLTreeNode<T> Node;public:AVLTree():_pRoot(nullptr){}// 在AVL树中插入值为data的节点boolInsert(const T& data){
        Node* newNode =newNode(data);if(_pRoot ==nullptr){//一开始的根就是平衡因子为0的
            _pRoot = newNode;returntrue;}//找到合适的根节点位置进行插入
        Node* cur = _pRoot;
        Node* parent =nullptr;//中序遍历是有序的，即左边比根小，右边比根大while(cur){
            parent = cur;if(cur->_data > data){
                cur = cur->_pLeft;}elseif(cur->_data < data){
                cur = cur->_pRight;}else{delete newNode;returnfalse;//键值冗余}}//cur最终在叶子节点,进行连接if(parent->_data > data){
            newNode->_pParent = parent;
            parent->_pLeft = newNode;}else{
            newNode->_pParent = parent;
            parent->_pRight = newNode;}//查看是否进行翻转//累加路径上的节点的bf值，查看是否需要翻转
        cur = newNode;while(cur->_pParent){
            Node* parent = cur->_pParent;if(parent->_pLeft == cur){
                parent->_bf--;if(parent->_bf ==-2){if(cur->_bf ==-1){//右旋RotateR(parent);break;}else{//左右双旋RotateLR(parent);break;}}elseif(parent->_bf ==0)//当更新到0的时候表明这颗子树已经平衡了，不会影响上面{break;}}else{
                parent->_bf++;if(parent->_bf ==2){if(cur->_bf ==1){//左旋即可RotateL(parent);break;}else{// -1 右左双旋RotateRL(parent);break;}}elseif(parent->_bf ==0)//当更新到0的时候表明这颗子树已经平衡了，不会影响上面{break;}}
            cur = parent;}returntrue;}voidcengxu(){
        queue<Node*> q;
        cout << _pRoot->_data << endl;
        q.push(_pRoot);while(!q.empty()){
            Node* front = q.front();
            q.pop();if(front)
                cout << front->_data <<" ";else
                cout <<"nullptr"<<" ";if(front)
                q.push(front->_pLeft);if(front)
                q.push(front->_pRight);}}// AVL树的验证boolIsAVLTree(){return_IsAVLTree(_pRoot);}voidOrder(){_Order(_pRoot);}
    vector<int> v;void_Order(Node* node){if(node ==nullptr)return;_Order(node->_pLeft);
        cout << node->_data <<" ";
        v.push_back(node->_data);_Order(node->_pRight);}intHeight(Node* root){if(root ==nullptr)return0;int leftHeight =Height(root->_pLeft);int rightHeight =Height(root->_pRight);return leftHeight > rightHeight ? leftHeight +1: rightHeight +1;}bool_IsBalance(Node* root){if(root ==nullptr)returntrue;int leftHeight =Height(root->_pLeft);int rightHeight =Height(root->_pRight);if(rightHeight - leftHeight != root->_bf){
            cout <<"平衡因子异常:"<< root->_data <<" "<< root->_bf <<" real "<< rightHeight - leftHeight << endl;}returnabs(rightHeight - leftHeight)<2&&_IsBalance(root->_pLeft)&&_IsBalance(root->_pRight);}boolIsBalance(){return_IsBalance(_pRoot);}private:// 右单旋voidRotateR(Node* pParent)//pParent为bf不平衡的点{
        Node* left = pParent->_pLeft;
        Node* lleft = left->_pLeft;
        Node* pFather = pParent->_pParent;
        Node* lRight = left->_pRight;
        pParent->_pLeft = left->_pRight;if(lRight){
            lRight->_pParent = pParent;}
        left->_pRight = pParent;
        pParent->_pParent = left;
        left->_pParent = pFather;//若是根这里就指向NULL//调节平衡因子
        pParent->_bf =0;
        left->_bf =0;if(pFather ==nullptr){//说明调整的是根节点
            _pRoot = left;return;}if(pFather->_data > left->_data){
            pFather->_pLeft = left;}else{
            pFather->_pRight = left;}}// 左单旋voidRotateL(Node* pParent){
        Node* right = pParent->_pRight;
        Node* rRight = right->_pRight;
        Node* rLeft = right->_pLeft;
        Node* pFather = pParent->_pParent;if(rLeft){
            rLeft->_pParent = pParent;}
        pParent->_pRight = right->_pLeft;
        right->_pLeft = pParent;
        pParent->_pParent = right;
        right->_pParent = pFather;//调节平衡因子
        right->_bf = pParent->_bf =0;if(pFather ==nullptr){
            _pRoot = right;return;}if(pFather->_data > right->_data){
            pFather->_pLeft = right;}else{
            pFather->_pRight = right;}}// 右左双旋voidRotateRL(Node* pParent){
        Node* right = pParent->_pRight;
        Node* rLeft = right->_pLeft;int bf = rLeft->_bf;RotateR(right);RotateL(pParent);if(bf ==1){
            right->_bf =0;
            pParent->_bf =-1;}elseif(bf ==-1){
            right->_bf =1;
            pParent->_bf =0;}elseif(bf ==0){
            pParent->_bf = right->_bf = rLeft->_bf =0;}else{assert(false);}}// 左右双旋voidRotateLR(Node* pParent){
        Node* left = pParent->_pLeft;
        Node* lRight = left->_pRight;int bf = lRight->_bf;RotateL(left);RotateR(pParent);
        lRight->_bf =0;if(bf ==1){
            left->_bf =-1;
            pParent->_bf =0;}elseif(bf ==-1){
            left->_bf =0;
            pParent->_bf =1;}elseif(bf ==0){
            left->_bf = lRight->_bf = pParent->_bf =0;}else{assert(false);}}private:
    Node* _pRoot;};

Test.cc

测试随机插入若干个数据，查看是否依旧是红黑树

#include<iostream>usingnamespace std;#include"AVLTree.hpp"#include<vector>intmain(){srand(0);
    AVLTree<int> tree;for(int i =0; i <100000;++i){
        tree.Insert(rand()%100000);}if(tree.IsBalance()){
        cout <<"This is AVL Tree!!"<< endl;}else{
        cout <<"This is Not AVL Tree....."<< endl;}return0;}
标签： c++ 算法
本文转载自: https://blog.csdn.net/weixin_52344401/article/details/123216882
版权归原作者 ^jhao^ 所有， 如有侵权，请联系我们删除。
登录后发布评论

“【C++】一篇了解AVL实现细节（易懂图解版）”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

手把手教你安装AoiAWD

Spring Boot实现多数据库动态连接与配置指南

Spring Boot项目中结合MyBatis详细使用

MySQL 表的增删改查

Linux系统下Nginx的安装部署（两种方式）

【深度学习入门篇 ④ 】Pytorch实现手写数字识别

K8s 集群（kubeadm） CA 证书过期解决方案

文章导航