【特别篇】基于动态规划的武器指挥系统火力分配模型

【特别篇】武器指挥分配决策火力问题的代码复现

写在前面

本文仍然只是B站相关视频的代码复现，感兴趣的朋友可以进一步了解武器指挥分类决策火力问题的更多内容。

笔者简介:CCNU计科，喜欢看日漫唱歌看球和弹钢琴，还有偶像梅老板。

问题描述

火力分配属于一种资源分配问题，将供应量有限的若干种资源，比如说资金、机器设备、劳力、武器和兵力等，分配给若干个使用者，使得目标函数达到最优值。

问题就是，我方舰队计划用m枚同型导弹，攻击敌方的n个目标，每个目标的价值不同，被导弹击毁的概率仍然不同。问题是：如何合理分配使用导弹，使得毁伤敌人目标的效果可以最优?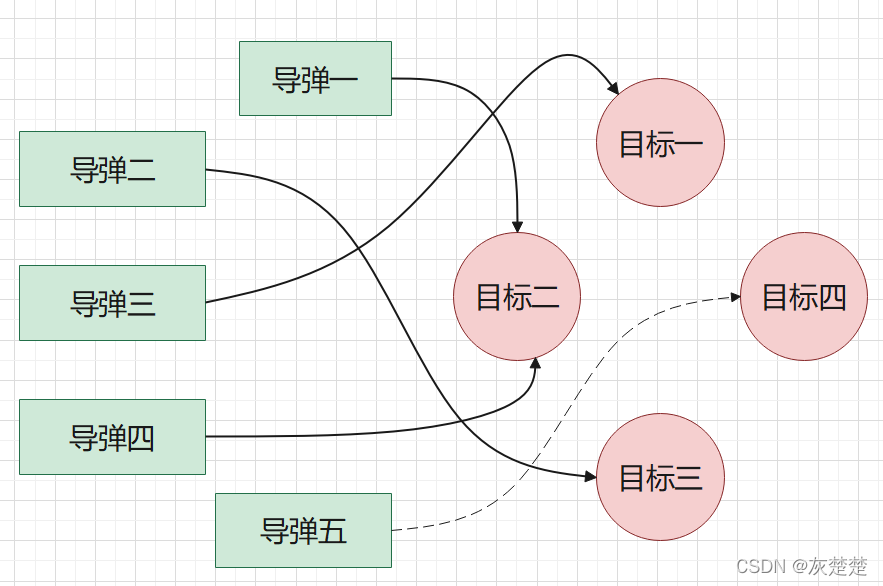

（一个战争导弹分配攻击目标的图示）

问题假设

建立模型，离不开现实方面的限制和假设，我们分析约定如下:

1)由于目标的防御能力、大小、距离、站位不同，导致每个目标的命中率不同。

2）攻击目标在敌方编队中的价值不同，比如说主目标通常攻击价值比较高，有的目标威胁程度比较强，因此在我们导弹资源有限的前提下，攻击敌方目标是具有优先级的。

3）作战阶段是可以划分为若干个互相联系的阶段；每个阶段都需要作出决策，并且遵循多米诺骨牌效应的方式影响着下一阶段的决策。也就是说后一阶段的决策是建立在前一阶段决策结果的基础上的。各个阶段所决定的决策构成一个序列，形成整个作战过程的方略。

4）在模型中，我们的每个阶段抽象为对目标1、目标2、直到目标n的导弹攻击。就是第一个阶段攻击目标1，第n个阶段攻击目标n这样依次类推下去。

模型建立

我方具有m枚同一型号的导弹，攻击敌方n个目标，每个目标的价值为Ck,且Xk为向第k个目标发射的导弹数量,且第k个目标被命中毁坏的概率为Pk，PK表达式如下：

Pk=1-e^(-ak*xk)

如果说我们要建立规划模型，那么可以书写如下：

目标函数: max V=Sum( Ck * (1-e ^ (-ak * xk )) ) (k=1…m)
s.t. Sum(Xk)=m ( Sum() 为求和符号 )
(k=1…m) Xk为整数，k=1,2,…,n

那你就要问了，这个Xk是什么东西呢?原来Xk就是表示第K阶段的决策变量，比如说第一阶段我打出2枚导弹，第二阶段我打出1枚导弹，第三阶段我一枚都不打出，直到第四阶段我打出2枚导弹，由此状态变量就是：

X1=2，X2=1，X3=0，X4=2

那么分配给第K个目标直至第n个目标的导弹总数用x表示就是:

x=Sum(Xi) (i=k…m)

这个表格可以怎么理解呢？哼哼，其实像xk这一系列的状态变量就是第k个阶段所使用的的导弹数量，而Xk’就是第k个阶段总导弹数量的剩余量。

然后呢，你怎么衡量导弹对第k个目标的毁伤效果呢？毕竟最好的情况就是击中一个目标就寄一个目标，但是这是有概率的，我们假设了Pk=1-e^(-ak*xk)的表达式。

其中ak可以理解为由目标的防御能力、大小、距离、站位不同等因素共同决定的参数，这是需要数据支撑和人为调整的。
由此，对第K个目标的毁伤效果衡量的函数可以表达为:

Vk(x)=Ck * ( 1- e ^ (-ak * xk ))

最后我们再规定一个目标最优函数fk(x),表示将x枚导弹分配给第K个目标直至第n个目标的毁伤效果。

请大家牢牢地记住以上几个表达式的含义，因为我们马上就要来到动态规划的模型建立了哈！

动态规划

我们先截个原视频里面的图用来表示模型：

其中fn(x)就是第n阶段对目标n的目标最优函数，就是第n个阶段的效能函数。

重点是第二个表达式该如何表示，通俗的说，我们是从后面向前面进行推导，fk+1(x-xk)表示了将(x-xk) 枚导弹分配给第K+1个目标直至第n个目标的最优毁伤效果。也就是说，我们需要得到第k个阶段的最佳毁伤效果，因为从第k+1个阶段到第n个阶段已经最优，但是潜在的限制仍然是x,也就是导弹剩余的分配量。

咋感觉你讲的云里雾里的，俺听不懂呢！没有关系，我们实例化来看看怎么解释。

战争火力模拟

身临其境，与敌军对弈，我军拥有导弹m=5,现在有敌人目标n=4,依据视频案例数据，我们给出Ck，ak的具体数值如下: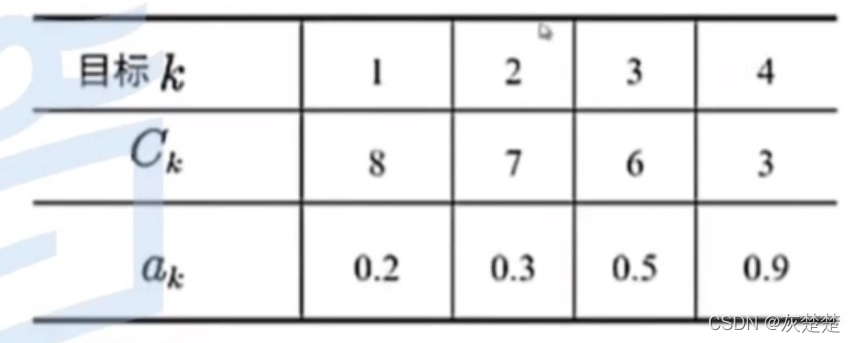

利用效能函数公式，计算出各个阶段的效能函数如图所示：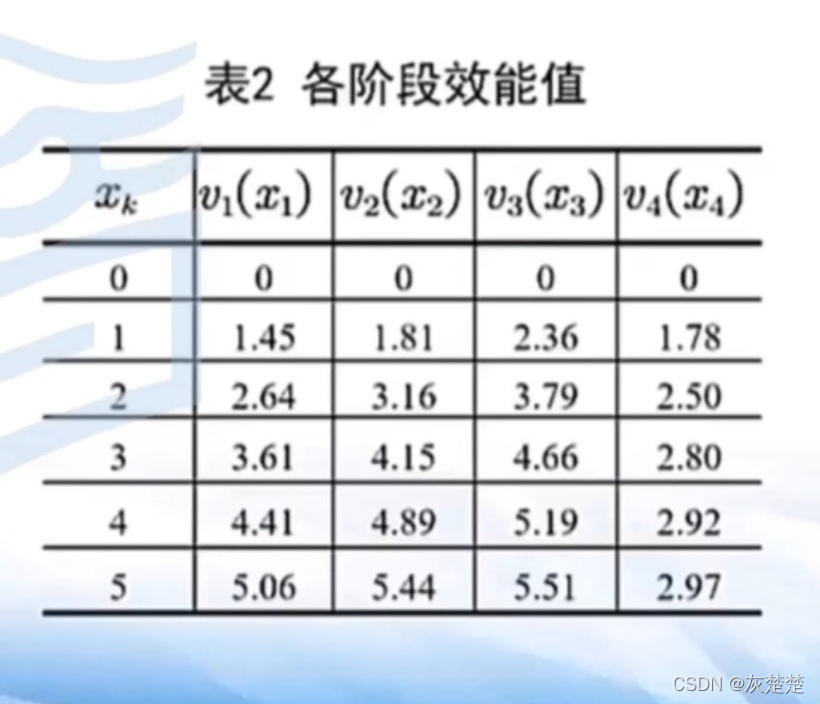

这样的话每个阶段用几枚导弹达到的效能都已经表现了出来。然后我们就是一个逆向思维，从第4阶段向第三阶段求解f3(x)的表达式值。
x4f4(x)0011.7822.5032.8042.9252.97
通过表格我们知道了第四阶段的目标最优函数值，可以确定f4,然后就是对于f3的确定了，那我们其实也是一个讨论的方式：

1.假设第3阶段只剩下1颗导弹，则：
f3(x)=[ v3(0) + f4(1) ] = 1.78 ------(1)

f3(x)=[ v3(1) + f4(0) ] = 2.36 -------(2)

2.假设第三阶段只剩下2颗导弹，则：
f3(x)=[ v3(0) + f4(2) ] = 2.5 ---------(3)

f3(x)=[ v3(1) + f4(1) ] = 4.14 ---------(4)

f3(x)=[ v3(2) + f4(0) ] = 3.79 ----------(5)

我们相当于将所有方案枚举出来，从第三阶段只剩下1颗，2颗，3颗，4颗，5颗，分五种情况讨论，然后取每种情况中的最大值作为该种情况下的最佳方案，然后就可以得到下表:
x3f300 **(第三阶段剩余0枚)**12.36 **(第三阶段剩余1枚)**14.14 (第三阶段剩余2枚)25.57 (第三阶段剩余3枚)36.44 (第三阶段剩余4枚)37.16 (第三阶段剩余5枚)
由此可以类比推理，得到每一个阶段的最优损伤效益值。最后形成的就是一个方案序列[1，1，2，1]。至此，导弹火力问题建模可以暂告一段落了。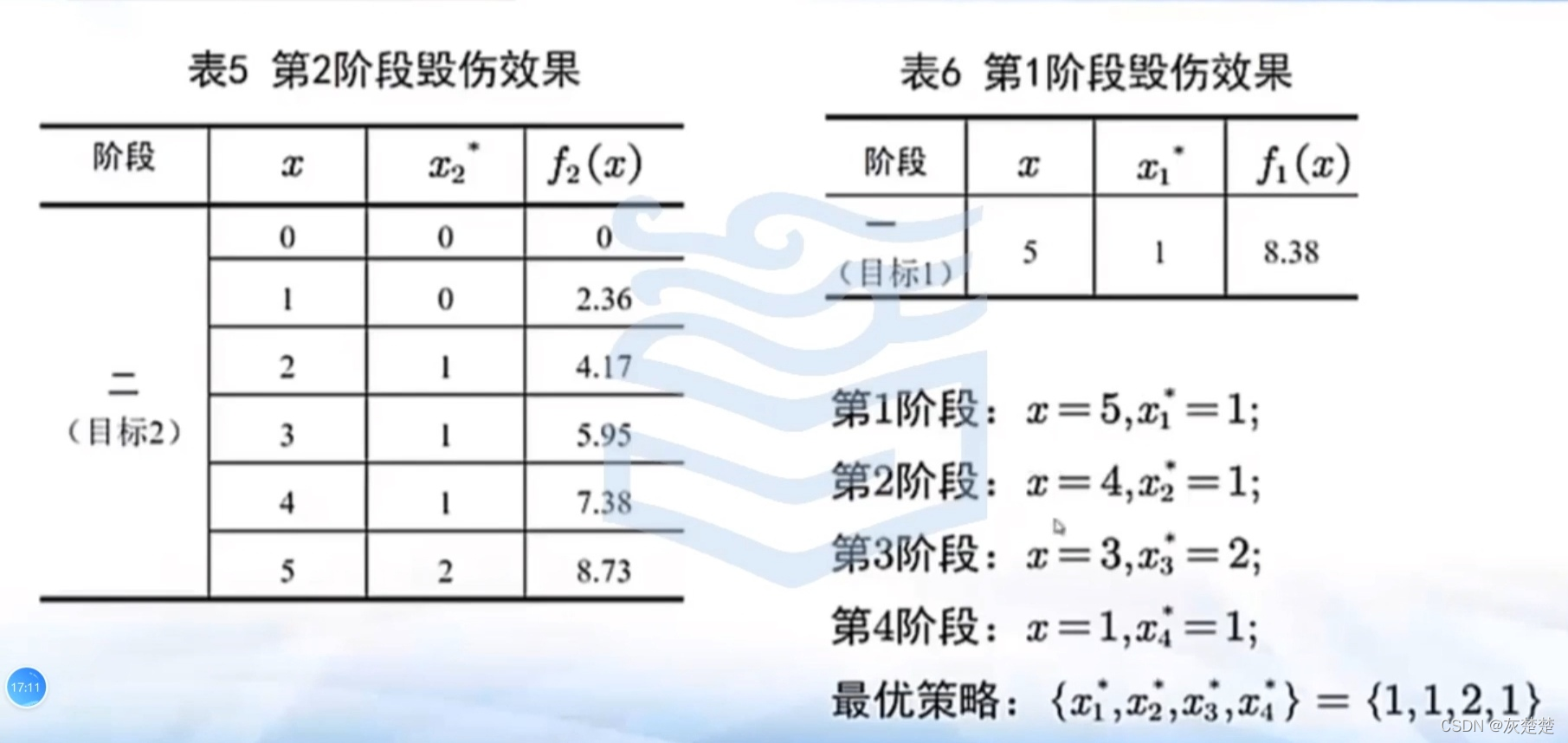

最后本例子的MATLAB代码将在代码区全部分享。
需要注意的是,我这里每个阶段攻击目标的价值和目标被攻击的概率是利用rand设置的分别在 [5,50] , [0,1] 区间里面的随机数，因此理解动态规划的一个工作流程是至关重要的一点。

代码区

n=4;%攻击的目标数量
m=5;%我方持有的导弹数量
c=rand(1,4)*(50-5)+5;%每个目标攻击价值
a=rand(1,4);%每个目标攻击概率
v=[];%效能函数
for i=0:5
    v=[v;c.*(1-exp(-a*i))];
end
%%由第四阶段求第三阶段
m3v=-inf;
m3i=-inf;
f3=[];
f3i=[];for i=1:5for j=0:i
f=v(j+1,3)+v(i-j+1,4);if f>m3v
m3v=f;
m3i=j+1;
end
end
f3=[f3,m3v];
f3i=[f3i,m3i];
 end
f3=[0;f3'];
f3i=f3i-1;v(:,3)=f3;%%由第3阶段求第2阶段
m3v=-inf;
m3i=-inf;
f2=[];
f2i=[];for i=1:5for j=0:i
f=v(j+1,2)+v(i-j+1,3);if f>m3v
m3v=f;
m3i=j+1;
end
end
f2=[f2,m3v];
f2i=[f2i,m3i];
 end
f2=[0;f2'];
f2i=f2i-1;v(:,2)=f2;%%由第2阶段求第1阶段
m3v=-inf;
m3i=-inf;
f1=[];
f1i=[];for i=1:5for j=0:i
f=v(j+1,1)+v(i-j+1,2);if f>m3v
m3v=f;
m3i=j+1;
end
end
f1=[f1,m3v];
f1i=[f1i,m3i];
 end
f1=[0;f1'];
f1i=f1i-1;v(:,1)=f1;
cc=[];%最优方案序列
[id1,id11]=max(f1)%id1为全局最大效益
cc=[cc,f1i(1,id11-1)]%id11用来找出全局最大效益下，第一阶段的导弹分配数

if id11-1-cc(1)>0%保证每一个阶段的导弹剩余量大于0
cc=[cc,f2i(1,id11-1-cc(1))]
end

if id11-1-cc(1)-cc(2)>0%保证每一个阶段的导弹剩余量大于0
cc=[cc,f3i(1,id11-1-cc(1)-cc(2))]
end

if id11-1-cc(1)-cc(2)-cc(3)>0%保证每一个阶段的导弹剩余量大于0
cc=[cc,m-cc(1)-cc(2)-cc(3)]
end