C++牛客周赛43题目分享（3）小红平分糖果，小红的完全平方数，小苯的字符串变化，小红的子数组排列判断

1.前言

哈喽大家好啊，就在刚刚的周日，结束了牛客周赛 Round 43，今天继续为大家分享一些题解，希望对大家有所帮助，也请大家多多支持我哦~

2.四道题目

2.1小红平分糖果

2.1.1题目描述

2.1.2输入描述

2.1.3输出描述

2.1.4示例

2.1.5代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

int main(){
    int n=0;
    scanf("%d",&n);
    if(n%2==0)printf("%d %d",n/2,n/2);
    else printf("-1");
    return 0;
} 

第一道题就是一道简单的签到题，认真审题就没有问题~

2.2小红的完全平方数

2.1.1题目描述

2.1.2输入描述

2.1.3输出描述

2.1.4示例

2.1.5代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;

void func()
{
    long long x;
    cin>>x;
    long long l=sqrt(x);
    long long r=l+1;
    if((x-l*l)%2==0)cout<<(x-l*l)/2;
    else cout<<(r*r-x)/2;
    
}
int main()
{
    func();
    return 0;
}

第二道题考了一道有关完全平方数的问题：

在解决这道题之前，我们需要先明白完全平方数的一个性质，每一个完全平方数都是由连续的自然数平方得出，由于自然数的顺序是奇数偶数交错，且奇数乘以奇数仍未奇数，偶数乘以偶数仍未偶数，因此，每一个完全平方数也是奇数偶数相交错。

---

在知晓这一个性质之后就可以开始敲代码了，先寻找输入的这个数在哪俩个相邻的完全平方数之间，然后寻找该数离哪一个完全平方数的距离是偶数，最后输出即可。

以上代码中是直接打印出了模拟出来的结果，可以先自己在演草本上写写。

2.3小苯的字符串变化

2.1.1题目描述

2.1.2输入描述

2.1.3输出描述

2.1.4示例

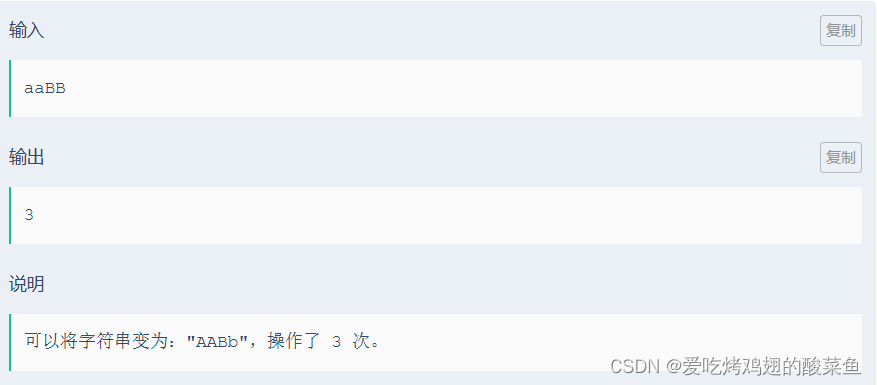
2.1.5代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;

const int N=100005;
char s[N];
int a[N],b[N];
int m=0,locate=0,ans=1e9;

int main(){
    scanf("%s",s);
    m=strlen(s);
    if(s[0]>='a'&&s[0]<='z')a[0]=1;

    for(int i=1;i<m;i++){
        if(s[i]>='a'&&s[i]<='z'){
            a[i]=a[i-1]+1;
        }
        else a[i]=a[i-1];
    }
    
    for(int j=m-1;j>=0;j--){
        if(s[j]>='A'&&s[j]<='Z'){
            b[j]=b[j+1]+1;
        }
        else b[j]=b[j+1];
    }
    
    for(int n=0;n<m-1;n++){
        ans=min(ans,a[n]+b[n+1]);
    }
    cout<<ans<<endl;
    return 0;
} 

这一道题有一点前缀和的感觉，接下来是题目思路：

根据题意，任何一个位置都可以作为那一个“分界点”，即前面小写字母（包括本分界点）都变成大写字母，后面的大写字母（不包括本分界点）都变成小写字母。因此根据这个逻辑，我们可以将每一个字母都作为“分界点”并利用循环分别计算前后大小写字母个数。

---

先按照题意输入，然后先进行第一个字母的判断（因为循环处可能会出现越界，所以将边界点拿出来单独处理），接着俩个循环（一个正向，一个反向）分别计算字母数量，最后再利用一个循环取所有分界点中，俩个字母数目相加的最小值，最后输出即可。

2.4小红的子数组排列判断

2.1.1题目描述

2.1.2输入描述

2.1.3输出描述

2.1.4示例

2.1.5代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

int n=0,k=0;//数组大小与连续子数组大小
int a[100005];//存储定义排列
int b[100005];//存储当下数字状态
int num=0;//存储当下k数组中有多少不同的数字
int ans=0;//记录答案

int main(){
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++)scanf("%d",&a[i]);
    
    for(int i=0;i<k;i++){
        b[a[i]]++;
        if(b[a[i]]==1)num++;
    }
    if(num==k)ans++;//判断前k个是否满足题意
    
    for(int i=k;i<n;i++){
        b[a[i-k]]--;
        if(b[a[i-k]]==0)num--;
        b[a[i]]++;
        if(b[a[i]]==1)num++;
        if(num==k)ans++;
    }
    cout<<ans<<endl;
    return 0;
} 

这道题当时拿到手里的时候，感觉题目很清晰但自己唯一能想到的方法就是暴力（就是一直不断利用for循环），但我也知道这样也会爆TLE，所以接下来给大家分享一个比较良好的算法整体思路如下：

---

先来为大家讲解一下题意：

我这里输入的数组与k值分别为：

数组：3 2 3 1 2 3 2 1 2 3 1 3

k值：3

我们从第一个开始往后模拟（每次往后递推一位）：

3 2 3不满足。2 3 1满足。3 1 2满足。1 2 3满足。2 3 2不满足。

3 2 1满足。2 1 2不满足。1 2 3满足。2 3 1满足。3 1 3不满足。

综上所述，输出结果应为6。

---

从以上的模拟我们应该能发现规律，每次往后地推一位只是少了第一个数多了最后一个数，在判断该子序列是否满足题意时也大可不必采用for循环大法，可以通过判断每位数出现的次数，如果出现的次数num刚好等于k，那么ans++；相反如果子序列中有重复的数，num<k，那么ans不做处理，最后输出即可。

---

（还有一点也需要提到的是，如果输入的数中有大于k的数字，应当continue，但对该题无影响，这样操作更加严谨）

3.小结

今天的这四道题虽然题目较为简单，但对平时解题时思路的拓展仍有借鉴意义，看完了不要忘了点个赞喔。感谢大家的支持~