连通块（dfs）java实现

前言

连通块问题属于图的深度优先遍历dfs，本文章通过求连通块的个数简单案例，来介绍dfs解决连通块问题。

例题链接

http://oj.hzjingma.com/p/29?view=classic

例题中给到的是char类型地图，' . ' 代表不通路，' W ' 代表可连通，具体情况根据题目给的进行修改。

什么是连通块

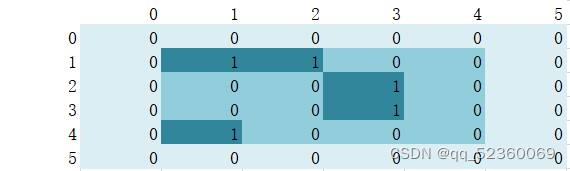
如图整个表格为一个55二维数组，用来表示整个地图，白色填充为二维数组下标，最外层浅绿色代表地图的边界（为什么创建边界下文有提到），较为深颜色的为存放数据的二维数组，即下标（1~4）（1~4）。而颜色最深的块就是连通块，图中给出的就有三个连通块（上下左右连通，不考虑斜对连通）。

具体思路

除了行数列数以及开辟二维数组地图，还需要一个与地图同样大小的二维数组visitied，用来表示当前节点是否已经被访问过了。具体思路同图的dfs类似，当遍历到一个结点为1表示该节点可以连通（根据题目给的可能不同）并且没被访问过就进行深度遍历。

具体看代码。

代码

import java.util.Scanner;
/**
 * 注意本例题中 
 * char[][]map地图   值为' . ' 代表不通，' W '代表可以连通
 * int[][] visitied访问标记，初始值0未访问，1已访问
 * @author lenovo
 *
 */

public class Main {
    static int n,m,ans;
    static char[][] map;
    static int[][] vistied;
    static int[][] step= {{1,0},{0,1},{-1,0},{0,-1}};
    /*
     * 上下左右移动遍历搜索
     *  1 ,0 表示 x + 1 ，y + 0 向右移动，其他同理
     *  如果为八向连通 则加上, { 1, 1 }, { 1, -1 }, { -1, 1 }, { -1, -1 } 代表斜向移动
     */
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        n=sc.nextInt();
        m=sc.nextInt();
        map=new char[n+2][m+2];
        vistied=new int[n+2][m+2];
        //初始化地图，创建边界
        for (int i = 0; i <= n+1; i++) {
            map[i][0] = '.';
            map[i][m+1] = '.';
        }
        for (int i = 0; i <= m+1; i++) {
            map[0][i] = '.';
            map[n+1][i] = '.';
        }
        //录入数据图（1~n）*（1~m）
        for (int i = 1; i <= n; i++) {
            String s=sc.next();
            int k=0;
            for (int j = 1; j <= m; j++) {
                map[i][j]=s.charAt(k++);
            }
        }
        //从1-n 1-m一次遍历整张数据图
        for (int x = 1; x <=n; x++) {
            for (int y =1; y <=m; y++) {
                //如果当前节点为'W'可以连通 并且为被访问则说明存在一个连通块
                if(vistied[x][y] ==0 && map[x][y] == 'W') {
                    ans++;//连接块数量+1
                    vistied[x][y] = 1;//当前节点标记为已经访问，以免重复判断
                    dfs(x,y);//进行深度优先遍历，将与其连通的所有节点都标记为已经访问。
                    //遍历完后从(1,1)到下一个节点(1,2)继续遍历，一次类推，直到所有节点全遍历完。
                }
            }
        }
        System.out.println(ans);
    }
    private static void dfs(int x, int y) {
        /**
         * step.length - 1 = 3
         * 0 1 2 3 四步代表上下左右均走一遍
         */
        for (int i = 0; i <=(step.length - 1); i++) {
            int newx=x+step[i][0]; //x移动
            int newy=y+step[i][1];//y移动
            //如果移动后的节点 为 'W'可连通，并且未访问，则以移动后的节点为起点继续移动
            if(map[newx][newy] =='W' && vistied[newx][newy] ==0) {
                vistied[newx][newy] = 1;//标记为已访问
                dfs( newx, newy);
            }
        }
    }
    
}

注意

   在实际应用时，为了防止当结点位于边界时，例如结点下标为(0,0)，其左结点下标为(-1,0),这时-1会越界。因此开辟二维数组的大小总是比题目中给到的n*m多两行，即开辟（n+2）*(m+2)大小的二维数组。