目录
列生成(Column generation)
是一种解决大型线性程序的有效算法。
相关教程
- 【从零开始】coin-or/CoinUtils Osi Clp Cgl Cbc源码构建debug(CLion/CMake)
相关文献
- Column generation(wikipedia)
- 干货 | 10分钟带你彻底了解column generation(列生成)算法的原理附java代码
- 列生成和分支定价
- 线性规划技巧: 列生成(Column Generation)
- 列生成算法原理(单纯形基础)
- 列生成(Column Generation)算法
- 【Column Generation思考-02】|从对偶的角度理解Cutting Stock Problem【更新版本】
- Gilmore P C, Gomory R E. A linear programming approach to the cutting-stock problem[J]. Operations research, 1961, 9(6): 849-859.
- 运筹说 第21期 | 算法介绍之列生成算法
前言
之前一直想跟大家分享一下
列生成(Column generation)
,也全网搜了许多文档、视频、论文等。大部分教程抽象程度较高,需要具备大量的基础知识才能看明白,于是写一篇尽可能0基础上手的分享,希望能帮到也在从事相关行业的你。
一定有人会问,有没有行生成算法?当然有啦!!!有机会之后给大家分享!!!——@小猪快跑
从一个例子出发:Cutting Stock Problem
问题描述
卖家有3种长度的木材:9cm(5元),14cm(9元),16cm(10元)。
买家需要木材:4cm(30根),5cm(20根),7cm(40根)。
于是卖家需要通过
切割木材
满足买家的需求,而且卖家希望
成本最低
从而达到受益最大。
分析
首先我们来简单思考下,一根9cm的木材能有多少种切法满足买家需要的4cm,5cm,7cm
cost(元)切前木材长度(cm)4cm木材数量5cm木材数量7cm木材数量5910059200590105911059001
本着不浪费的中华传统美德,显然
第二行的切法比第一行更好
一些哟(^U^)ノ~YO
我们一般习惯称一种切割方法为
cutting pattern
。
好啦,之后就非常easy的搞定之后的(只保留比较好的pattern)。
All Cutting Pattern:
cost(元)切前木材长度(cm)4cm木材数量5cm木材数量7cm木材数量符号59200
x
1
x_1
x159110
x
2
x_2
x259001
x
3
x_3
x3914300
x
4
x_4
x4914210
x
5
x_5
x5914120
x
6
x_6
x6914101
x
7
x_7
x7914011
x
8
x_8
x8914002
x
9
x_9
x91016400
x
10
x_{10}
x101016201
x
11
x_{11}
x111016111
x
12
x_{12}
x121016030
x
13
x_{13}
x13
于是我们只需要从
All Cutting Pattern
里面确定
每个Pattern需要几次
就行了。(举个例子:比如
x
1
=
30
\bm{x_1=30}
x1=30代表我们使用第1种切法切了30根9cm长度的木材)。
我们目标是用
最少的钱
完成买家的需求,也就是每个Pattern的
c
o
s
t
×
数量
\bm{cost\times }\textbf{数量}
cost×数量的总和。
5 x 1 + 5 x 2 + 5 x 3 + 9 x 4 + 9 x 5 + 9 x 6 + 9 x 7 + 9 x 8 + 9 x 9 + 10 x 10 + 10 x 11 + 10 x 12 + 10 x 13 5x_1+5x_2+5x_3+9x_4+9x_5+9x_6+9x_7+9x_8+9x_9+10x_{10}+10x_{11}+10x_{12}+10x_{13} 5x1+5x2+5x3+9x4+9x5+9x6+9x7+9x8+9x9+10x10+10x11+10x12+10x13
另外呢我们需要
满足买家数量上的要求
。
4cm要超过30根:
2 x 1 + x 2 + 0 x 3 + 3 x 4 + 2 x 5 + x 6 + x 7 + 0 x 8 + 0 x 9 + 4 x 10 + 2 x 11 + x 12 + 0 x 13 ≥ 30 2x_1+x_2+0x_3+3x_4+2x_5+x_6+x_7+0x_8+0x_9+4x_{10}+2x_{11}+x_{12}+0x_{13}\geq 30 2x1+x2+0x3+3x4+2x5+x6+x7+0x8+0x9+4x10+2x11+x12+0x13≥30
5cm要超过20根:
0 x 1 + x 2 + 0 x 3 + 0 x 4 + x 5 + 2 x 6 + 0 x 7 + x 8 + 0 x 9 + 0 x 10 + 0 x 11 + x 12 + 3 x 13 ≥ 20 0x_1+x_2+0x_3+0x_4+x_5+2x_6+0x_7+x_8+0x_9+0x_{10}+0x_{11}+x_{12}+3x_{13}\geq 20 0x1+x2+0x3+0x4+x5+2x6+0x7+x8+0x9+0x10+0x11+x12+3x13≥20
7cm要超过70根:
0 x 1 + 0 x 2 + x 3 + 0 x 4 + 0 x 5 + 0 x 6 + x 7 + x 8 + 2 x 9 + 0 x 10 + x 11 + x 12 + 0 x 13 ≥ 40 0x_1+0x_2+x_3+0x_4+0x_5+0x_6+x_7+x_8+2x_9+0x_{10}+x_{11}+x_{12}+0x_{13}\geq 40 0x1+0x2+x3+0x4+0x5+0x6+x7+x8+2x9+0x10+x11+x12+0x13≥40
建模
Master Problem(MP)
根据上面的分析,我们已经有了决策变量
x
i
x_i
xi,我们有了目标函数
最少的钱
,我们也有了相应的约束
满足买家数量上的要求
,于是乎我们可以来建模啦!!!
定义决策变量
x i \bm{x_i} xi为使用第 i i i种Pattern的根数。 min 5 x 1 + 5 x 2 + 5 x 3 + 9 x 4 + 9 x 5 + 9 x 6 + 9 x 7 + 9 x 8 + 9 x 9 + 10 x 10 + 10 x 11 + 10 x 12 + 10 x 13 \min{5x_1+5x_2+5x_3+9x_4+9x_5+9x_6+9x_7+9x_8+9x_9+10x_{10}+10x_{11}+10x_{12}+10x_{13}} min5x1+5x2+5x3+9x4+9x5+9x6+9x7+9x8+9x9+10x10+10x11+10x12+10x13 s . t . s.t. s.t. 2 x 1 + x 2 + 0 x 3 + 3 x 4 + 2 x 5 + x 6 + x 7 + 0 x 8 + 0 x 9 + 4 x 10 + 2 x 11 + x 12 + 0 x 13 ≥ 30 2x_1+x_2+0x_3+3x_4+2x_5+x_6+x_7+0x_8+0x_9+4x_{10}+2x_{11}+x_{12}+0x_{13}\geq 30 2x1+x2+0x3+3x4+2x5+x6+x7+0x8+0x9+4x10+2x11+x12+0x13≥30 0 x 1 + x 2 + 0 x 3 + 0 x 4 + x 5 + 2 x 6 + 0 x 7 + x 8 + 0 x 9 + 0 x 10 + 0 x 11 + x 12 + 3 x 13 ≥ 20 0x_1+x_2+0x_3+0x_4+x_5+2x_6+0x_7+x_8+0x_9+0x_{10}+0x_{11}+x_{12}+3x_{13}\geq 20 0x1+x2+0x3+0x4+x5+2x6+0x7+x8+0x9+0x10+0x11+x12+3x13≥20 0 x 1 + 0 x 2 + x 3 + 0 x 4 + 0 x 5 + 0 x 6 + x 7 + x 8 + 2 x 9 + 0 x 10 + x 11 + x 12 + 0 x 13 ≥ 40 0x_1+0x_2+x_3+0x_4+0x_5+0x_6+x_7+x_8+2x_9+0x_{10}+x_{11}+x_{12}+0x_{13}\geq 40 0x1+0x2+x3+0x4+0x5+0x6+x7+x8+2x9+0x10+x11+x12+0x13≥40 x i ∈ N x_i\in\mathbb{N} xi∈N每一列:
一种可行的切割方案需要被执行的次数,或者
多少根棒材使用这种切割方案每一行:
一种棒材的需求必须要被满足
Restricted Master Problem(RMP)
有时候
MP
的规模会非常大,于是我们考虑如果先用几种
Pattern
得到一个可行的方案(可能不是最优解),然后我们有了这个可行解后再去依次看如果增加其他
Pattern
会不会有更好的解,而直接求解
MP
可能在给定时间内无法得到可行解。
于是顺着这个思路我们构建
RMP
(要注意我们选择的
Pattern
至少能得到一个可行解):
定义决策变量
x i \bm{x_i} xi为使用第 i i i种Pattern的根数。 min 5 x 1 + 5 x 2 + 5 x 3 \min{5x_1+5x_2+5x_3} min5x1+5x2+5x3 s . t . s.t. s.t. 2 x 1 + x 2 + 0 x 3 ≥ 30 2x_1+x_2+0x_3\geq 30 2x1+x2+0x3≥30 0 x 1 + x 2 + 0 x 3 ≥ 20 0x_1+x_2+0x_3\geq 20 0x1+x2+0x3≥20 0 x 1 + 0 x 2 + x 3 ≥ 40 0x_1+0x_2+x_3\geq 40 0x1+0x2+x3≥40 x i ∈ N x_i\in\mathbb{N} xi∈N
Restricted Linear Master Problem(RLMP)
常规的列生成方法都是解决LP问题的,这时候我们做一些适当的松弛(也就是
x
i
∈
N
x_i\in\mathbb{N}
xi∈N变成
x
i
≥
0
x_i\geq 0
xi≥0)。
于是顺着这个思路我们构建
RLMP
(要注意
RLMP
的可行解并不一定是
RMP
的可行解,但我们只需要把解上取整即可):
定义决策变量
x i \bm{x_i} xi为使用第 i i i种Pattern的根数。 min 5 x 1 + 5 x 2 + 5 x 3 \min{5x_1+5x_2+5x_3} min5x1+5x2+5x3 s . t . s.t. s.t. 2 x 1 + x 2 + 0 x 3 ≥ 30 2x_1+x_2+0x_3\geq 30 2x1+x2+0x3≥30 0 x 1 + x 2 + 0 x 3 ≥ 20 0x_1+x_2+0x_3\geq 20 0x1+x2+0x3≥20 0 x 1 + 0 x 2 + x 3 ≥ 40 0x_1+0x_2+x_3\geq 40 0x1+0x2+x3≥40 x i ≥ 0 x_i\geq 0 xi≥0
然后我们可以用
LP求解器
直接求解上述模型(这里我用
Clp
来举例,当然你可以使用你喜欢的求解器)
(为了排版整洁方便阅读,我会把代码放在文末)
直接运行得到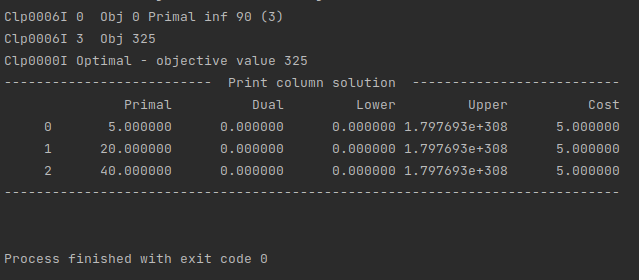
理论上来说我们应该对结果
上取整,但我们将在得到松弛后的
MP解之后再上取整会更方便高效,所以这里我们不进行
上取整(不过好像刚好解是整数Σ(⊙▽⊙"a——@小猪快跑):
O b j e c t i v e v a l u e = 325 Objective \: value = 325 Objectivevalue=325 x 1 = 5 x_1 = 5 x1=5 x 2 = 20 x_2 = 20 x2=20 x 3 = 40 x_3 = 40 x3=40我们试图来解释一下solution的含义:
用5个Pattern 1(也就是说选了5根9cm的木材,每根都切成2个4cm),类似的又用了20个Pattern 2和40个Pattern 3,这样的选择能使我们总花费最少——325元。
Dual of Restricted Linear Master Problem
现在我们从另一个角度来考虑
RMP。
【卖家】直接购买成品(切割后的木材),转手卖给客户,类似中间商。
【卖家】目标:最多花多少钱购买成品挣得要比自己生产多。
【卖家】约束:需要给成品定一个心理价位。这些心理价位必须满足:对于任意切割方案,购买成品的钱 <= 自己生产的钱。(比如说,卖家花5元买到1根9cm的木材可以切割成2个4cm成品,也就是说卖家如果直接购买2个4cm的成品价格超过5元那不如自己生产了。写成公式:
2 y 1 ≤ 5 2y_1\leq 5 2y1≤5,其中 y 1 \bm{y_1} y1为4cm木材的心理价格)————————————————————————————————————————————————————————
定义决策变量y i \bm{y_i} yi分别为4cm(30根),5cm(20根),7cm(40根)木材的心理价格。 max 30 y 1 + 20 y 2 + 40 y 3 \max{30y_1+20y_2+40y_3} max30y1+20y2+40y3 s . t . s.t. s.t. 2 y 1 + 0 y 2 + 0 y 3 ≤ 5 2y_1+0y_2+0y_3\leq 5 2y1+0y2+0y3≤5 y 1 + y 2 + 0 y 3 ≤ 5 y_1+y_2+0y_3\leq 5 y1+y2+0y3≤5 0 y 1 + 0 y 2 + y 3 ≤ 5 0y_1+0y_2+y_3\leq 5 0y1+0y2+y3≤5 y i ≥ 0 y_i\geq 0 yi≥0
直接求解: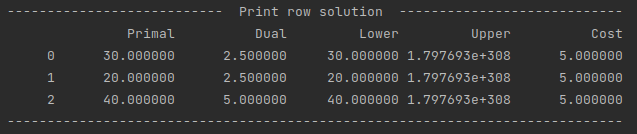
O b j e c t i v e v a l u e = 325 Objective \: value = 325 Objectivevalue=325 y 1 = 2.5 y_1 = 2.5 y1=2.5 y 2 = 2.5 y_2 = 2.5 y2=2.5 y 3 = 5.0 y_3 = 5.0 y3=5.0我们试图来解释一下solution的含义:
4cm、5cm、7cm成品木材的心理价格分别是2.5元、2.5元、5元,最多花325元购买成品挣得要比自己生产多。也就是说只要
价格比2.5元、2.5元、5元低,卖家就赚了。
Subproblem
- 单纯形法检验数的含义:该产品(变量)的市场价格与该产品的隐含成本之差。市场价格高于隐含成本,即检验数大于零时,则可将该产品投入生产。
- 原问题检验数对应其对偶问题的一个基解
如果你知道检验数的概念,会很快理解subproblem,不过在这里我会假设你不知道,试图用最简单的方法让你理解——@小猪快跑
在
dual问题中我们计算出成品的心理价格。接下来我们想知道是不是存在更省钱的Pattern。
首先我们来思考一下如何判定一个Pattern是不是更省钱。
例子1:9cm的木材完全浪费掉也是一种Pattern,但一根9cm的木材要5元,也就是说卖家损失了5元。
例子2:Pattern 9:14cm木材(9元)切割成2根7cm成品(使用Pattern 1、2、3的7cm心理价格是5元)。也就是卖家只用Pattern 1、2、3这三种切割方法的时候,只要用低于5元的价格购买7cm再卖掉就比自己切割赚钱了,而如果加上了Pattern 9,卖家如果用5元的价格就不如自己直接用Pattern 9来的赚钱,而是必须低于4.5元(9元/2)的价格购买7cm再卖掉才比自己切割赚钱。
有了上面两个例子我们已经逐渐清晰如何去判定一个Pattern是不是更省钱。
也就是说我们的目标是去寻找一个新Pattern:新Pattern切割后的成品在老Pattern下的心理价格 > 新Pattern的价格定义决策变量
a j \bm{a_{j}} aj是新Pattern切割后4cm,5cm,7cm木材的数量。新Pattern切割后的成品在老Pattern下的心理价格【
2.5 a 1 + 2.5 a 2 + 5 a 3 2.5a_1+2.5a_2+5a_3 2.5a1+2.5a2+5a3】>新Pattern的价格【9元(14cm)】即:
2.5 a 1 + 2.5 a 2 + 5 a 3 > 9 2.5a_1+2.5a_2+5a_3>9 2.5a1+2.5a2+5a3>9 ⇒ 9 − ( 2.5 a 1 + 2.5 a 2 + 5 a 3 ) < 0 \Rightarrow 9-(2.5a_1+2.5a_2+5a_3)<0 ⇒9−(2.5a1+2.5a2+5a3)<0(不等号左边我们一般称之为检验数,这就是我们常说的
检验数判定解是否是最优解)
这里我们用一个约束转换成目标函数的小技巧:令z = 9 − ( 2.5 a 1 + 2.5 a 2 + 5 a 3 ) z=9-(2.5a_1+2.5a_2+5a_3) z=9−(2.5a1+2.5a2+5a3),如果 min z \min z minz比0还大,那说明不存在 z > 0 z>0 z>0的解,也就是不存在更省钱的Pattern。新Pattern切割后总长度不能超过原始木材长度:
4 a 1 + 5 a 2 + 7 a 3 ≤ 14 4a_1+5a_2+7a_3\leq 14 4a1+5a2+7a3≤14综合起来就是:
min 9 − ( 2.5 a 1 + 2.5 a 2 + 5 a 3 ) \min{9-(2.5a_1+2.5a_2+5a_3)} min9−(2.5a1+2.5a2+5a3) 4 a 1 + 5 a 2 + 7 a 3 ≤ 14 4a_1+5a_2+7a_3\leq 14 4a1+5a2+7a3≤14
于是我们分别建立9cm、14cm、16cm的Subproblem :
————————————————————————————————————————————————————————
Subproblem 1(9cm,5元)
定义决策变量a j \bm{a_{j}} aj是Pattern切割后4cm,5cm,7cm木材的数量。 min z = 5 − ( 2.5 a 1 + 2.5 a 2 + 5 a 3 ) \min{z=5-(2.5a_1+2.5a_2+5a_3)} minz=5−(2.5a1+2.5a2+5a3) s . t . s.t. s.t. 4 a 1 + 5 a 2 + 7 a 3 ≤ 9 4a_1+5a_2+7a_3\leq 9 4a1+5a2+7a3≤9 a i ∈ N a_i\in\mathbb{N} ai∈N求解得:
a = ( 2 , 0 , 0 ) T , z = 0 a=(2,0,0)^T, z=0 a=(2,0,0)T,z=0————————————————————————————————————————————————————————
Subproblem 2(14cm,9元)
定义决策变量a j \bm{a_{j}} aj是Pattern切割后4cm,5cm,7cm木材的数量。 min z = 9 − ( 2.5 a 1 + 2.5 a 2 + 5 a 3 ) \min{z=9-(2.5a_1+2.5a_2+5a_3)} minz=9−(2.5a1+2.5a2+5a3) s . t . s.t. s.t. 4 a 1 + 5 a 2 + 7 a 3 ≤ 14 4a_1+5a_2+7a_3\leq 14 4a1+5a2+7a3≤14 a i ∈ N a_i\in\mathbb{N} ai∈N求解得:
a = ( 0 , 0 , 2 ) T , z = − 1 \bm{a=(0,0,2)^T, z=-1} a=(0,0,2)T,z=−1————————————————————————————————————————————————————————
Subproblem 3(16cm,10元)
定义决策变量a j \bm{a_{j}} aj是Pattern切割后4cm,5cm,7cm木材的数量。 min z = 10 − ( 2.5 a 1 + 2.5 a 2 + 5 a 3 ) \min{z=10-(2.5a_1+2.5a_2+5a_3)} minz=10−(2.5a1+2.5a2+5a3) s . t . s.t. s.t. 4 a 1 + 5 a 2 + 7 a 3 ≤ 16 4a_1+5a_2+7a_3\leq 16 4a1+5a2+7a3≤16 a i ∈ N a_i\in\mathbb{N} ai∈N求解得:
a = ( 4 , 0 , 0 ) T , z = 0 a=(4,0,0)^T, z=0 a=(4,0,0)T,z=0
迭代
我们发现Subproblem 2的
z < 0 z<0 z<0,于是我们把 a = ( 0 , 0 , 2 ) T a=(0,0,2)^T a=(0,0,2)T这个Pattern加入到RLMP中,因为这就是我们找到的更省钱的Pattern。
定义决策变量x i \bm{x_i} xi为使用第 i i i种Pattern的根数。 min 5 x 1 + 5 x 2 + 5 x 3 + 9 x 9 \min{5x_1+5x_2+5x_3+9x_9} min5x1+5x2+5x3+9x9 s . t . s.t. s.t. 2 x 1 + x 2 + 0 x 3 + 0 x 9 ≥ 30 2x_1+x_2+0x_3+0x_9\geq 30 2x1+x2+0x3+0x9≥30 0 x 1 + x 2 + 0 x 3 + 0 x 9 ≥ 20 0x_1+x_2+0x_3+0x_9\geq 20 0x1+x2+0x3+0x9≥20 0 x 1 + 0 x 2 + x 3 + 2 x 9 ≥ 40 0x_1+0x_2+x_3+2x_9\geq 40 0x1+0x2+x3+2x9≥40 x i ≥ 0 x_i\geq 0 xi≥0
求解后得到:
O b j e c t i v e v a l u e = 305 Objective \: value = 305 Objectivevalue=305 x 1 = 5 x_1 = 5 x1=5 x 2 = 20 x_2 = 20 x2=20 x 3 = 0 x_3 = 0 x3=0 x 9 = 20 x_9 = 20 x9=20 y 1 = 2.5 y_1 = 2.5 y1=2.5 y 2 = 2.5 y_2 = 2.5 y2=2.5 y 9 = 4.5 y_9 = 4.5 y9=4.5由于
x 3 = 0 x_3=0 x3=0,所以我们可以从模型中舍去 x 3 x_3 x3。于是我们分别建立9cm、14cm、16cm的Subproblem :
————————————————————————————————————————————————————————
Subproblem 1(9cm,5元)
定义决策变量a j \bm{a_{j}} aj是Pattern切割后4cm,5cm,7cm木材的数量。 min z = 5 − ( 2.5 a 1 + 2.5 a 2 + 4.5 a 9 ) \min{z=5-(2.5a_1+2.5a_2+4.5a_9)} minz=5−(2.5a1+2.5a2+4.5a9) s . t . s.t. s.t. 4 a 1 + 5 a 2 + 7 a 9 ≤ 9 4a_1+5a_2+7a_9\leq 9 4a1+5a2+7a9≤9 a i ∈ N a_i\in\mathbb{N} ai∈N求解得:
a = ( 2 , 0 , 0 ) T , z = 0 a=(2,0,0)^T, z=0 a=(2,0,0)T,z=0————————————————————————————————————————————————————————
Subproblem 2(14cm,9元)
定义决策变量a j \bm{a_{j}} aj是Pattern切割后4cm,5cm,7cm木材的数量。 min z = 9 − ( 2.5 a 1 + 2.5 a 2 + 4.5 a 9 ) \min{z=9-(2.5a_1+2.5a_2+4.5a_9)} minz=9−(2.5a1+2.5a2+4.5a9) s . t . s.t. s.t. 4 a 1 + 5 a 2 + 7 a 9 ≤ 14 4a_1+5a_2+7a_9\leq 14 4a1+5a2+7a9≤14 a i ∈ N a_i\in\mathbb{N} ai∈N求解得:
a = ( 0 , 0 , 2 ) T , z = 0 a=(0,0,2)^T, z=0 a=(0,0,2)T,z=0————————————————————————————————————————————————————————
Subproblem 3(16cm,10元)
定义决策变量a j \bm{a_{j}} aj是Pattern切割后4cm,5cm,7cm木材的数量。 min z = 10 − ( 2.5 a 1 + 2.5 a 2 + 4.5 a 9 ) \min{z=10-(2.5a_1+2.5a_2+4.5a_9)} minz=10−(2.5a1+2.5a2+4.5a9) s . t . s.t. s.t. 4 a 1 + 5 a 2 + 7 a 9 ≤ 16 4a_1+5a_2+7a_9\leq 16 4a1+5a2+7a9≤16 a i ∈ N a_i\in\mathbb{N} ai∈N求解得:
a = ( 4 , 0 , 0 ) T , z = 0 a=(4,0,0)^T, z=0 a=(4,0,0)T,z=0
所有的Subproblem目标
z ≥ 0 z \geq 0 z≥0,那就说明不存在更好的Pattern,于是最终的解(记得上取整):
x 1 = 5 , x 2 = 20 , x 9 = 20 x_1 = 5, x_2 = 20, x_9 = 20 x1=5,x2=20,x9=20
以上整个算法过程我们就称之为——列生成
列生成:Cutting Stock Problem
本节需要一定的运筹学基础,但如果你已经看完上文的话,我相信理解起来也会非常简单了。——@小猪快跑
提出Gomory割的大佬Gomory在IBM的时候,与另一个大佬Gilmore 共同提出了著名的Column Generation:
参考文献:
@article{gilmore1961linear,
title={A linear programming approach to the cutting-stock problem},
author={Gilmore, Paul C and Gomory, Ralph E},
journal={Operations research},
volume={9},
number={6},
pages={849–859},
year={1961},
publisher={INFORMS}
}
问题描述
卖家有
n
n
n种长度的木材:
L
i
L_i
Li m(
c
i
c_i
ci元)
买家需要
m
m
m种长度的木材:
l
i
l_i
li m(
d
i
d_i
di根)
于是卖家需要通过
切割木材
满足买家的需求,而且卖家希望
成本最低
从而达到受益最大。
建模
Master Problem(MP)
min
∑
i
=
1
n
c
i
x
i
s
.
t
.
∑
i
=
1
n
a
i
j
x
i
≥
b
i
,
j
=
1
,
2
,
.
.
.
,
m
x
i
∈
N
,
∀
i
\begin{aligned} & \min{\sum_{i=1}^n c_ix_i} \\ & s.t. \sum_{i=1}^n a_{ij}x_i \geq b_i , j=1,2,...,m \\ & x_i\in\mathbb{N}, \forall i \end{aligned}
mini=1∑ncixis.t.i=1∑naijxi≥bi,j=1,2,...,mxi∈N,∀i
Restricted Master Problem(RMP)
min
∑
i
=
1
k
c
i
x
i
s
.
t
.
∑
i
=
1
k
a
i
j
x
i
≥
b
i
,
j
=
1
,
2
,
.
.
.
,
m
x
i
∈
N
,
∀
i
\begin{aligned} & \min{\sum_{i=1}^k c_ix_i} \\ & s.t. \sum_{i=1}^k a_{ij}x_i \geq b_i , j=1,2,...,m \\ & x_i\in\mathbb{N}, \forall i \end{aligned}
mini=1∑kcixis.t.i=1∑kaijxi≥bi,j=1,2,...,mxi∈N,∀i
也就是MP问题变量数从
n
n
n减少到
k
k
k个,需要注意我们强制了
x
i
(
i
>
k
)
x_i(i>k)
xi(i>k)的变量为非基变量。
Dual of Restricted Master Problem
为了在Subproblem中计算检验数:
σ
j
=
c
j
−
c
B
B
−
1
a
j
\sigma_j = c_j-c_BB^{-1}a_j
σj=cj−cBB−1aj,我们需要计算出
c
B
B
−
1
c_BB^{-1}
cBB−1,一般来说他有两重含义:
- 通过求解RMP问题得到的影子价格(shadow price)。
- 通过求解RMP对偶问题得到的对偶变量(dual variable)。
我们一般使用第2种对偶问题求解。因为RMP一般变量极多,而单纯形法对于变量多的问题求解很困难。
原问题的变量对应对偶问题的约束,目标系数对应约束边界,约束矩阵倒转过来。
所以在对偶问题上就没有这个困扰。
Subproblem
min
c
j
−
∑
ω
i
a
i
j
s
.
t
.
∑
i
=
1
m
l
i
a
i
≤
L
j
a
i
≥
0
,
∀
i
\begin{aligned} & \min c_j-\sum \omega_i a_{ij} \\ & s.t. \sum_{i=1}^m l_{i}a_i \leq L_j \\ & a_i\geq 0, \forall i \end{aligned}
mincj−∑ωiaijs.t.i=1∑mliai≤Ljai≥0,∀i
迭代
检验数小于0的话,就把Pattern加入列,进行下一次迭代,直到所有检验数大于等于0。最后上取整结果即可。
流程图
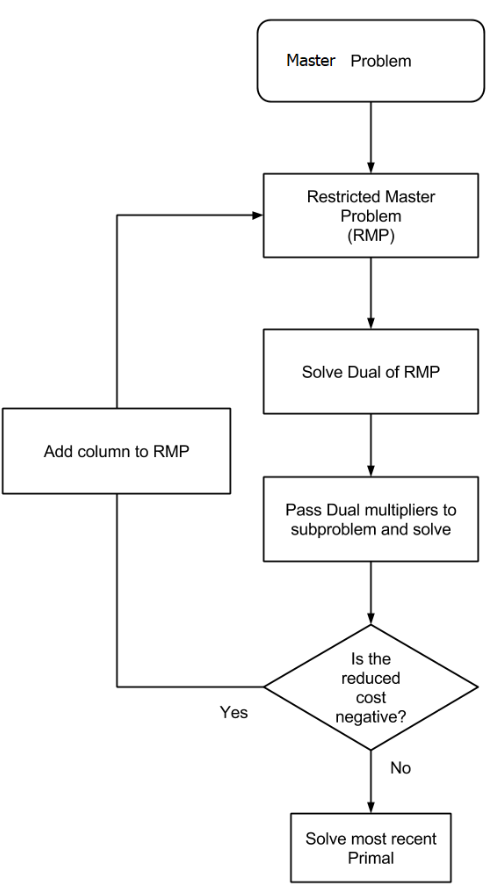
总结
- 列生成算法主要用于求解
变量多,但大部分变量取值为0的线性规划问题。 - 总体思路是先选出小部分变量构建
RMP(也就是其余变量取值都是0)快速得到一个可行解,之后再通过Subproblem计算检验数(reduced cost)寻找有没有更好的变量加入模型再次求解,直到找不到更好的变量。 - 为什么增加变量可以让目标值更好呢?原问题增加变量=>对偶问题增加约束=>对偶问题最优值不变或者变小(对偶问题是max问题,约束越多可行域越小,自然目标函数优度下降)=>原问题最优值不变或者变小(对偶问题和原问题最优解是一样的) 事实上,我们需要找的变量是能在对偶问题中让最优解不满足新增的约束。
版权归原作者 ymzhu385 所有, 如有侵权,请联系我们删除。