hash原理与应用
一、背景知识
在了解hash算法之前,先思考如下问题:
- 使用 word 文档时,word 如何判断某个单词是否拼写正确?
- 网络爬虫程序,怎么让它不去爬相同的 url 页面?
- 垃圾邮件过滤算法如何设计?
- 公安办案时,如何判断某嫌疑人是否在网逃名单中?
- 缓存穿透问题如何解决?
了解平衡二叉树: 平衡二叉树查找数据采用二分查找,每次查找排除一半。平衡的目的是增删改之后,保证下次搜索能够稳定排除一半的数据。
平衡二叉树增删改查的时间复杂度为
O
(
log
2
n
)
O(\log_2n)
O(log2n)。比如,100万个节点,最多比较 20 次;10 亿
个节点,最多比较 30 次;
平衡二叉树通过比较保证有序,通过每次排除一半的元素达到快速索引的目的。
#mermaid-svg-ylFmJioFy5jjoSnt {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-ylFmJioFy5jjoSnt .error-icon{fill:#552222;}#mermaid-svg-ylFmJioFy5jjoSnt .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-ylFmJioFy5jjoSnt .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-ylFmJioFy5jjoSnt .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-ylFmJioFy5jjoSnt .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-ylFmJioFy5jjoSnt .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-ylFmJioFy5jjoSnt .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-ylFmJioFy5jjoSnt .marker{fill:#333333;stroke:#333333;}#mermaid-svg-ylFmJioFy5jjoSnt .marker.cross{stroke:#333333;}#mermaid-svg-ylFmJioFy5jjoSnt svg{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-ylFmJioFy5jjoSnt .label{font-family:"trebuchet ms",verdana,arial,sans-serif;color:#333;}#mermaid-svg-ylFmJioFy5jjoSnt .cluster-label text{fill:#333;}#mermaid-svg-ylFmJioFy5jjoSnt .cluster-label span{color:#333;}#mermaid-svg-ylFmJioFy5jjoSnt .label text,#mermaid-svg-ylFmJioFy5jjoSnt span{fill:#333;color:#333;}#mermaid-svg-ylFmJioFy5jjoSnt .node rect,#mermaid-svg-ylFmJioFy5jjoSnt .node circle,#mermaid-svg-ylFmJioFy5jjoSnt .node ellipse,#mermaid-svg-ylFmJioFy5jjoSnt .node polygon,#mermaid-svg-ylFmJioFy5jjoSnt .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-ylFmJioFy5jjoSnt .node .label{text-align:center;}#mermaid-svg-ylFmJioFy5jjoSnt .node.clickable{cursor:pointer;}#mermaid-svg-ylFmJioFy5jjoSnt .arrowheadPath{fill:#333333;}#mermaid-svg-ylFmJioFy5jjoSnt .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-ylFmJioFy5jjoSnt .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-ylFmJioFy5jjoSnt .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-ylFmJioFy5jjoSnt .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-ylFmJioFy5jjoSnt .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-ylFmJioFy5jjoSnt .cluster text{fill:#333;}#mermaid-svg-ylFmJioFy5jjoSnt .cluster span{color:#333;}#mermaid-svg-ylFmJioFy5jjoSnt div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-ylFmJioFy5jjoSnt :root{--mermaid-font-family:"trebuchet ms",verdana,arial,sans-serif;}
二分查找
有序数组
平衡二叉树
平衡多路搜索树
多层级有序链表
跳表
红黑树
AVL
B树
B+树
二、散列表
平衡二叉树通过比较让结构有序,从而提升收搜索效率。在平衡二叉树中,搜索数据时总是对key进行比较,如果在海量数据中使用这种方式,搜索效率会很低。
相较于平衡二叉树,散列表是一种不比较key,而是根据key计算key在表中的位置的数据结构;是key和其所在存储地址的映射关系。散列表通过此方式达到快速索引的目的。
注意:散列表的节点中key-value是存储在一起的。
structnode{void*key;void*val;structnode*next;};
2.1、散列表的构成
(1)hash函数。hash函数的作用是映射,把key映射到具体存储的位置,通过key找到其存储地址。
(2)数组。key通过hash函数找到数组的位置(hash出来的值要对数组长度取余),该位置就是存储key-value的地方。
2.2、hash函数
映射函数
Hash(key)=addr
;
hash
函数可能会把两个或两个以上的不同 key 映射到同一地址,这种情况称之为冲突(或者hash 碰撞);hash函数的作用是将Key映射为地址。
注意,hash函数可能会把两个或两个以上的不同key映射到同一地址,这种现象称为hash冲突。
hash函数的选择:
- 计算速度快。因为如果计算速度慢,还不如直接比较Key。
- 强随机分布(等概率、均匀地分布在整个地址空间)
- 常用的hash函数: - murmurhash1:速度快、但质量一般。- murmurhash2:速度比较快、质量比较好,因此是使用最广泛的一种。- murmurhash3:计算速度慢,但质量是最好的。- siphash: redis6.0 当中使用,rust 等大多数语言选用的 hash 算法来实现 hashmap。- cityhash 等都具备强随机分布性。- 不同hash算法的效率、速度、质量测试:测试地址。
- siphash 主要解决字符串接近的强随机分布性 。
2.3、散列表的操作流程
散列表的插入操作和搜索操作都要经过hash函数找到key对应的存储地址。首先,key经过hash函数hash(key)得到一个64bit或32bit的整数maddr;然后maddr对数组长度取余,得到的值就是存储节点的位置。
- 插入流程:key-value对要存储到散列表中,首先将key通过hash函数进行hash,生成64位或32位的一个整数;然后利用这个整数对数组长度进行取余,得到的值必定能落在数组的某个槽位中;最后在该槽位增加一个节点,完成数据的存储池。
- 搜索流程:同样的,也是通过将key通过hash函数进行hash运算生成一个64位或32位的整数;然后利用这个整数对数组长度进行取余,得到该值所在数组的某个槽位。
- hans运算是一个线性运算,相同的key通过运算后得到的值总是相同的。相同的值对数组长度取余必定落在相同的数组槽位。
#mermaid-svg-DsIq0rQhIJVKaJkQ {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-DsIq0rQhIJVKaJkQ .error-icon{fill:#552222;}#mermaid-svg-DsIq0rQhIJVKaJkQ .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-DsIq0rQhIJVKaJkQ .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-DsIq0rQhIJVKaJkQ .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-DsIq0rQhIJVKaJkQ .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-DsIq0rQhIJVKaJkQ .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-DsIq0rQhIJVKaJkQ .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-DsIq0rQhIJVKaJkQ .marker{fill:#333333;stroke:#333333;}#mermaid-svg-DsIq0rQhIJVKaJkQ .marker.cross{stroke:#333333;}#mermaid-svg-DsIq0rQhIJVKaJkQ svg{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-DsIq0rQhIJVKaJkQ .label{font-family:"trebuchet ms",verdana,arial,sans-serif;color:#333;}#mermaid-svg-DsIq0rQhIJVKaJkQ .cluster-label text{fill:#333;}#mermaid-svg-DsIq0rQhIJVKaJkQ .cluster-label span{color:#333;}#mermaid-svg-DsIq0rQhIJVKaJkQ .label text,#mermaid-svg-DsIq0rQhIJVKaJkQ span{fill:#333;color:#333;}#mermaid-svg-DsIq0rQhIJVKaJkQ .node rect,#mermaid-svg-DsIq0rQhIJVKaJkQ .node circle,#mermaid-svg-DsIq0rQhIJVKaJkQ .node ellipse,#mermaid-svg-DsIq0rQhIJVKaJkQ .node polygon,#mermaid-svg-DsIq0rQhIJVKaJkQ .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-DsIq0rQhIJVKaJkQ .node .label{text-align:center;}#mermaid-svg-DsIq0rQhIJVKaJkQ .node.clickable{cursor:pointer;}#mermaid-svg-DsIq0rQhIJVKaJkQ .arrowheadPath{fill:#333333;}#mermaid-svg-DsIq0rQhIJVKaJkQ .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-DsIq0rQhIJVKaJkQ .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-DsIq0rQhIJVKaJkQ .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-DsIq0rQhIJVKaJkQ .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-DsIq0rQhIJVKaJkQ .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-DsIq0rQhIJVKaJkQ .cluster text{fill:#333;}#mermaid-svg-DsIq0rQhIJVKaJkQ .cluster span{color:#333;}#mermaid-svg-DsIq0rQhIJVKaJkQ div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-DsIq0rQhIJVKaJkQ :root{--mermaid-font-family:"trebuchet ms",verdana,arial,sans-serif;}
指针数组
0
1
2
3
4
5
6
7
node
node
node
node
node
散列表的指针数组通常是动态增加的过程,最开始定义的数组长度为4,当数据增多时将长度翻倍变成8,以此类推,16、32、… 。随着删除元素越来越多,散列表的数组长度也会自动缩小。
注意,散列表是无序的,通过牺牲有序性来提高它的效率。而平衡二叉树是通过保证有序性来提高它的搜索效率。散列表通过映射的关系不保证有序性,但可以查询某个节点在哪个位置。
2.4、hash冲突
冲突产生原因: 在数组大小不变情况下,随着添加的元素(数据)的越来越多,必然产生冲突;而且hash是随机性的,这也可能会产生冲突。
比如把n+1个元素放入n大小的数组,势必有一个空间需要存放两个元素,这就是冲突。另外,hash是随机的,产生的数对数组长度取余很可能相同,这也会冲突。
举个经典的数学原理:抽屉原理。桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。 抽屉原理的一般含义为:“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1个元素放到n个集合中去,其中必定有一个集合里至少有两个元素。” 抽屉原理有时也被称为鸽巢原理。它是组合数学中一个重要的原理。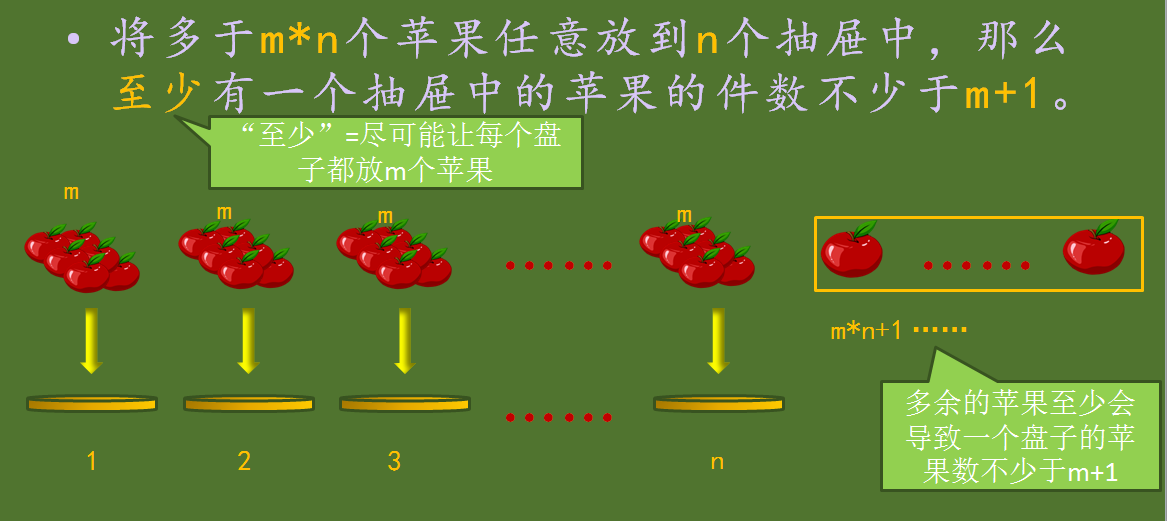
hash冲突的定义:多个key经过hash函数,然后对数组长度取余,落在同一个数组槽位,这时就产生冲突。
描述hash冲突激烈程度和存储密度的参数/系数:负载因子。负载因子用于描述冲突的激烈程度和存储的密度;负载因子越小,冲突概率越小,负载因子越大,冲突概率越大。
计算公式:负载因子=数组存储元素的个数 / 数组长度。
2.5、hash冲突的处理
解决冲突的方法有很多,开源框架中比较常用的有:链表法 / 拉链法、开放寻址法等。
一般,链表法和开放寻址法适用于负载因子在合理范围内的情况,即数组存储元素的个数小于数组长度的情况。
(1)链表法 / 拉链法。 使用场景:redis、STL的unordered_*系列、java的一些容器中 等等。
链表法是常用的处理冲突的方式。通过引用链表来处理hash冲突;散列表中的数组是指针数组,通过一个链表,将落在同一个槽位的元素连接起来;即将冲突元素用链表链接起来。
但可能出现极端情况,冲突元素比较多,该冲突链表过长;这个时候可以考虑将链表转换为红黑树、最小堆;由原来链表时间复杂度
O
(
n
)
O(n)
O(n)转换为红黑树时间复杂度
O
(
log
2
n
)
O(\log_2n)
O(log2n);可以采用超过 256(经验值)个节点的时候将链表结构转换为红黑树或堆结构。
#mermaid-svg-5vQpnKcz7XTw8ohz {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-5vQpnKcz7XTw8ohz .error-icon{fill:#552222;}#mermaid-svg-5vQpnKcz7XTw8ohz .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-5vQpnKcz7XTw8ohz .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-5vQpnKcz7XTw8ohz .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-5vQpnKcz7XTw8ohz .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-5vQpnKcz7XTw8ohz .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-5vQpnKcz7XTw8ohz .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-5vQpnKcz7XTw8ohz .marker{fill:#333333;stroke:#333333;}#mermaid-svg-5vQpnKcz7XTw8ohz .marker.cross{stroke:#333333;}#mermaid-svg-5vQpnKcz7XTw8ohz svg{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-5vQpnKcz7XTw8ohz .label{font-family:"trebuchet ms",verdana,arial,sans-serif;color:#333;}#mermaid-svg-5vQpnKcz7XTw8ohz .cluster-label text{fill:#333;}#mermaid-svg-5vQpnKcz7XTw8ohz .cluster-label span{color:#333;}#mermaid-svg-5vQpnKcz7XTw8ohz .label text,#mermaid-svg-5vQpnKcz7XTw8ohz span{fill:#333;color:#333;}#mermaid-svg-5vQpnKcz7XTw8ohz .node rect,#mermaid-svg-5vQpnKcz7XTw8ohz .node circle,#mermaid-svg-5vQpnKcz7XTw8ohz .node ellipse,#mermaid-svg-5vQpnKcz7XTw8ohz .node polygon,#mermaid-svg-5vQpnKcz7XTw8ohz .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-5vQpnKcz7XTw8ohz .node .label{text-align:center;}#mermaid-svg-5vQpnKcz7XTw8ohz .node.clickable{cursor:pointer;}#mermaid-svg-5vQpnKcz7XTw8ohz .arrowheadPath{fill:#333333;}#mermaid-svg-5vQpnKcz7XTw8ohz .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-5vQpnKcz7XTw8ohz .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-5vQpnKcz7XTw8ohz .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-5vQpnKcz7XTw8ohz .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-5vQpnKcz7XTw8ohz .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-5vQpnKcz7XTw8ohz .cluster text{fill:#333;}#mermaid-svg-5vQpnKcz7XTw8ohz .cluster span{color:#333;}#mermaid-svg-5vQpnKcz7XTw8ohz div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-5vQpnKcz7XTw8ohz :root{--mermaid-font-family:"trebuchet ms",verdana,arial,sans-serif;}
指针数组
0
1
2
3
4
5
6
7
node
node
node
node
node
(2)开放寻址法。使用场景:布隆过滤器。
开放寻址法将所有的元素都存放在哈希表的数组中(这个数组不再是指针数组),不使用额外的数据结构。一般使用线性探查的的思路解决:
- 当插入新元素时,使用hash函数在hash表中定位元素的位置;
- 检查数组中该槽位索引是否存在元素,如果该槽位为空,则插入数据,否则进入(3)。
- 在第二点检测的槽位索引上加一定步长接着检查第二点;加步长有以下几种:- i+1,i+2,i+3,i+4,…,i+n。这种方式缺点比较大,当key非常接近时,落在数组的槽位都是非常接近的,一直往下找就可能造成由O(1)的时间复杂度退化成O(n)的时间复杂度。- i- 1 2 1^2 12,i+ 2 2 2^2 22,i- 3 2 3^2 32,i+ 4 2 4^2 42,…。对上面的方式进行改进,虽然可以缓解hash聚集,但不能解决hash聚集问题。当hash聚集多了之后,也会慢慢的生成hash聚集问题。- 双重hash。解决hash聚集现象,本质上是线性探查的的思路。前两种都会产生同类hash聚集,也就是近似值它的hash值也近似,那么它的数组槽位也靠近,形成 hash 聚集;第一种同类聚集冲突在前,第二种只是将聚集冲突延后; 可以使用双重哈希来解决上面出现hash聚集现象。比如,在.net HashTable类的hash函数Hk定义如下: Hk(key) = [GetHash(key) + k * (1 +(((GetHash(key) >> 5) + 1) %(hashsize – 1)))] % hashsize 在此 (1 + (((GetHash(key) >> 5) + 1) %(hashsize – 1))) 与 hashsize互为素数(两数互为素数表示两者没有共同的质因⼦);执⾏了 hashsize 次探查后,哈希表中的每⼀个位置都有且只有⼀次被访问到,即对于给定的 key,对哈希表中的同⼀位置不会同时使⽤Hi 和 Hj。
(3)扩容和缩容。
上面两种解决hash冲突的方式都是负载因子在合理范围内的情况。当负载因子不在合理范围内是,即数组存储元素的个数大于数组长度的情况,可以使用扩容和缩容的方式避免hash冲突。
- 当used > size,即要使用的空间大于数组的长度,这时就需要通过扩容来避免或降低冲突。扩容通常采用翻倍扩容。
- 当used < 0.1 * size,即要使用的空间远远小于数组的长度,这时就需要缩容;缩容不能解决冲突,只能节约空间,减少内存浪费。
- rehash,重新hash。因为容量发生了改变,前面解释过key在数组的位置是通过key % size的方式;所以,需要重新做key % new_size找到key的槽位,然后重新放到新的数组中去。
#mermaid-svg-A6qgCz4GDbl9HmU7 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-A6qgCz4GDbl9HmU7 .error-icon{fill:#552222;}#mermaid-svg-A6qgCz4GDbl9HmU7 .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-A6qgCz4GDbl9HmU7 .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-A6qgCz4GDbl9HmU7 .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-A6qgCz4GDbl9HmU7 .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-A6qgCz4GDbl9HmU7 .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-A6qgCz4GDbl9HmU7 .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-A6qgCz4GDbl9HmU7 .marker{fill:#333333;stroke:#333333;}#mermaid-svg-A6qgCz4GDbl9HmU7 .marker.cross{stroke:#333333;}#mermaid-svg-A6qgCz4GDbl9HmU7 svg{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-A6qgCz4GDbl9HmU7 .label{font-family:"trebuchet ms",verdana,arial,sans-serif;color:#333;}#mermaid-svg-A6qgCz4GDbl9HmU7 .cluster-label text{fill:#333;}#mermaid-svg-A6qgCz4GDbl9HmU7 .cluster-label span{color:#333;}#mermaid-svg-A6qgCz4GDbl9HmU7 .label text,#mermaid-svg-A6qgCz4GDbl9HmU7 span{fill:#333;color:#333;}#mermaid-svg-A6qgCz4GDbl9HmU7 .node rect,#mermaid-svg-A6qgCz4GDbl9HmU7 .node circle,#mermaid-svg-A6qgCz4GDbl9HmU7 .node ellipse,#mermaid-svg-A6qgCz4GDbl9HmU7 .node polygon,#mermaid-svg-A6qgCz4GDbl9HmU7 .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-A6qgCz4GDbl9HmU7 .node .label{text-align:center;}#mermaid-svg-A6qgCz4GDbl9HmU7 .node.clickable{cursor:pointer;}#mermaid-svg-A6qgCz4GDbl9HmU7 .arrowheadPath{fill:#333333;}#mermaid-svg-A6qgCz4GDbl9HmU7 .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-A6qgCz4GDbl9HmU7 .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-A6qgCz4GDbl9HmU7 .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-A6qgCz4GDbl9HmU7 .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-A6qgCz4GDbl9HmU7 .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-A6qgCz4GDbl9HmU7 .cluster text{fill:#333;}#mermaid-svg-A6qgCz4GDbl9HmU7 .cluster span{color:#333;}#mermaid-svg-A6qgCz4GDbl9HmU7 div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-A6qgCz4GDbl9HmU7 :root{--mermaid-font-family:"trebuchet ms",verdana,arial,sans-serif;}
扩容
rehash
缩容
旧数组的key重新映射,搬到新数组中,释放旧数组的内存
2.6、STL unordered_* 散列表的实现
在 STL 中 unordered_map、unordered_set、unordered_multimap、unordered_multiset 四个容器的底层实现都是散列表。
#mermaid-svg-9Tyfoebnzb3vHBZV {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-9Tyfoebnzb3vHBZV .error-icon{fill:#552222;}#mermaid-svg-9Tyfoebnzb3vHBZV .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-9Tyfoebnzb3vHBZV .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-9Tyfoebnzb3vHBZV .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-9Tyfoebnzb3vHBZV .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-9Tyfoebnzb3vHBZV .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-9Tyfoebnzb3vHBZV .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-9Tyfoebnzb3vHBZV .marker{fill:#333333;stroke:#333333;}#mermaid-svg-9Tyfoebnzb3vHBZV .marker.cross{stroke:#333333;}#mermaid-svg-9Tyfoebnzb3vHBZV svg{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-9Tyfoebnzb3vHBZV .label{font-family:"trebuchet ms",verdana,arial,sans-serif;color:#333;}#mermaid-svg-9Tyfoebnzb3vHBZV .cluster-label text{fill:#333;}#mermaid-svg-9Tyfoebnzb3vHBZV .cluster-label span{color:#333;}#mermaid-svg-9Tyfoebnzb3vHBZV .label text,#mermaid-svg-9Tyfoebnzb3vHBZV span{fill:#333;color:#333;}#mermaid-svg-9Tyfoebnzb3vHBZV .node rect,#mermaid-svg-9Tyfoebnzb3vHBZV .node circle,#mermaid-svg-9Tyfoebnzb3vHBZV .node ellipse,#mermaid-svg-9Tyfoebnzb3vHBZV .node polygon,#mermaid-svg-9Tyfoebnzb3vHBZV .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-9Tyfoebnzb3vHBZV .node .label{text-align:center;}#mermaid-svg-9Tyfoebnzb3vHBZV .node.clickable{cursor:pointer;}#mermaid-svg-9Tyfoebnzb3vHBZV .arrowheadPath{fill:#333333;}#mermaid-svg-9Tyfoebnzb3vHBZV .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-9Tyfoebnzb3vHBZV .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-9Tyfoebnzb3vHBZV .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-9Tyfoebnzb3vHBZV .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-9Tyfoebnzb3vHBZV .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-9Tyfoebnzb3vHBZV .cluster text{fill:#333;}#mermaid-svg-9Tyfoebnzb3vHBZV .cluster span{color:#333;}#mermaid-svg-9Tyfoebnzb3vHBZV div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-9Tyfoebnzb3vHBZV :root{--mermaid-font-family:"trebuchet ms",verdana,arial,sans-serif;}
STL
红黑树
散列表
set
map
multiset
multimap
unorder_set
unorder_map
unorder_multiset
unorder_multimap
原理图:
一般,hash table里面的槽位单独通过链表串联所属槽位的数据;STL散列表的槽位指针不再这么做,而是做了优化:将后面具体结点串成一个单链表,而槽位指针指向上一个的结点。
unordered_map的类定义如下:
template<class_Key,class_Tp,class_Hash= hash<_Key>,class_Pred= std::equal_to<_Key>,class_Alloc= std::allocator<std::pair<const _Key, _Tp>>>classunordered_map{typedef __umap_hashtable<_Key, _Tp, _Hash, _Pred, _Alloc> _Hashtable;
_Hashtable _M_h;}
看下_Hashtable具体定义:
template<bool _Cache>using __umap_traits = __detail::_Hashtable_traits<_Cache,false,true>;template<typename_Key,typename_Tp,typename_Hash= hash<_Key>,typename_Pred= std::equal_to<_Key>,typename_Alloc= std::allocator<std::pair<const _Key, _Tp>>,typename_Tr= __umap_traits<__cache_default<_Key, _Hash>::value>>using __umap_hashtable = _Hashtable<_Key, std::pair<const _Key, _Tp>,
_Alloc, __detail::_Select1st,
_Pred, _Hash,
__detail::_Mod_range_hashing,
__detail::_Default_ranged_hash,
__detail::_Prime_rehash_policy, _Tr>;
举个例子:
现在的hash table是空的,还没有数据插入,当第一个hash(key) % array_size插入时,假设这个hash(key) % array_size=4,那么4的
_hash_node_base*
指向头指针
_M_before_begin
,
_M_before_begin.next
等于新插入的
_hash_node_base*
;后面又来一个插入,假设hash(key) % array_size=1,那么1的
_hash_node_base*
指向头结点
_M_before_begin
,
_M_before_begin.next
等于新插入的
_hash_node_base*
,新插入的
_hash_node_base.next
等于4的
_hash_node_base
,4的槽位指针指向新插入的
_hash_node_base*
。目的是将所有的节点串成一个单链表,以便实现迭代器。当前槽位的指针指向上一个槽位的位置是为了方便进行头插法。
2.7、小结
散列表需要掌握的知识点:
- 散列表与其他数据结构的比较,比如平衡二叉树。平衡二叉树通过比较Key,增、删、改操作都要保证结构有序,稳定搜索时间复杂度在 O ( l o g 2 n ) O(log_2n) O(log2n)(二分查找)。而散列表是找key与存储位置的映射关系,整个过程是无序的。
- 散列表的组成:hash函数、数组、运算流程/算法;确定映射关系。
- 函数函数有映射的作用,选择hash时需要注意几点:计算速度快、强随机分布性。常用的hash函数会选择murmurhash2、cityhash、siphash。
- 散列表操作流程是根据hash(key) % size = index找到存储位置。既使参数hash冲突了,链表法的解决方案还是需要通过比较key来找到value。Java的hashmap会将其组织成一个最小堆结构,因为单链表的时间复杂度是O(n),通过将其转换为红黑树或堆的数据结构可以将时间复杂度降低到 O ( l o g 2 n ) O(log_2n) O(log2n)。这是一种优化思路。
- hash冲突中需要注意负载因子的重要性,以及解决冲突的方式。负载因子在合理范围内(负载因子小于1)可以使用链表法或开放寻址法解决hash冲突。负载因子不在合理范围内则可以使用扩容并进行rehash来解决hash冲突。
- 注意STL散列表的优化方案。
思维导图:
三、布隆过滤器 (Bloom Filter)
3.1、背景
无论是使用散列表还是平衡二叉树(红黑树、B树、B+树等)的数据结构,都存储了key-value值。而有些场景,内存是有限的,仅需要了解key是否存在,不想知道具体内容(value)。这时就需要布隆过滤器。
布隆过滤器是一种概率型数据结构,它的特点是高效的插入和查询,能确定某个字符串一定存在或者可能存在。
布隆过滤器不存储具体数据,所以占用空间小,查询结果存在误差,但误差可控,同时不支持删除操作。
布隆过滤器的使用场景:
(1)一个巨大的数据文件,需要知道是否存在某个key,如果把整个文件读取进行查找,这个效率就比较低。那么可以添加一个布隆过滤器,插入数据时对key做标识,查询key是否存在时直接查询key是否在布隆过滤器,从而判断key是不是存在文件中。布隆过滤器仅仅只能判断key是否存在,不能获得value值。
(2)一个数据库查询,想要查询数据库中是否存在key,可以添加一个布隆过滤器,查询key时直接查询布隆过滤器,不需要IO操作,大大提升查询效率。
3.2、布隆过滤器的构成
布隆过滤器的原理本质上和散列表是一样的。但布隆过滤器为了节约内存,不是使用的数组,而是使用的位图(bitmap)。位图的特点是它的槽位只有两种状态:0或者1。
(1)位图。bit的数组,实现方式有多种。
// 例如
vector<char> bitmap;// 一个字节,8个bit位uint64_t bitmap;
(2)n个hash函数。
映射关系计算公式:m %
2
n
2^n
2n = m &(
2
n
−
1
2^n-1
2n−1)
举例:
使用
byte buf[8]
构建64 bit 的位图,那么n=i*8+j;假设hash(key)=173,先对总长度
8
×
8
8\times8
8×8 = 64取余:n=173%64=173&63=45;然后对宽度8进行取余:j=n%8=45%8=5;最后再对宽度8进行整除:i=n/8=45/8=5。因此得到坐标(5,5)位置将其置 1。
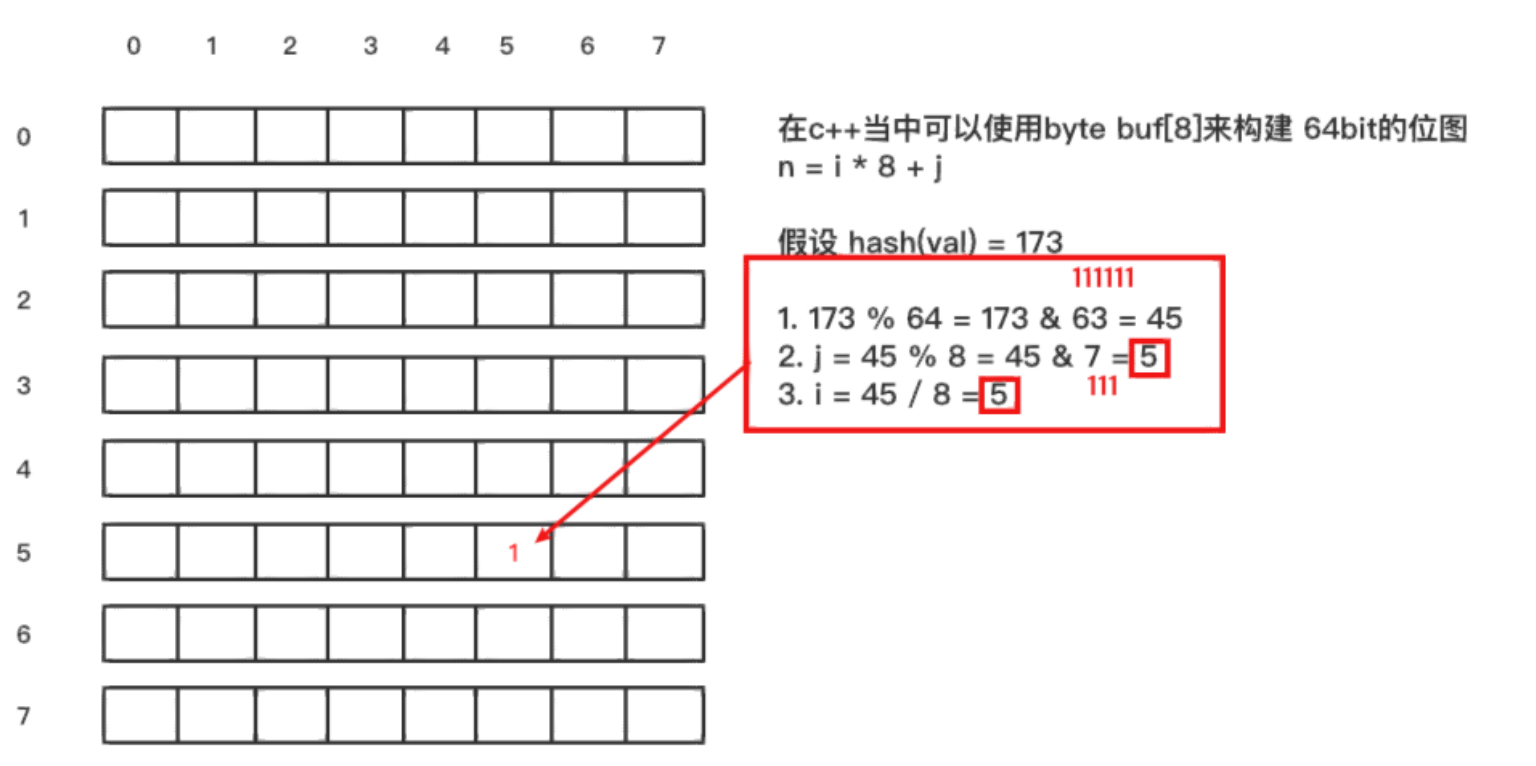
3.3、布隆过滤器原理
当一个元素加入位图时,通过k个hash函数将元素映射到位图的k个点,并把它们置1;当检索时,再通过k个hash函数运算检查位图的k个点是否都为1;如果有不为1的点,那么认为该key不存在;如果全部为1,则可能存在。
布隆过滤器是不支持删除操作的,原因在于:
- 在位图中每个槽位只有两种状态(0或者1),一个槽位被置为1,但不确定它被设置了多少次;也不知道被多少个key hash映射而来;以及具体被哪个hash函数映射而来。
- 只要有一个槽位为0,则key一定不存在;如果key映射的所有槽位都为1,不能说明一定存在,只能说明可能存在(假阳率)。
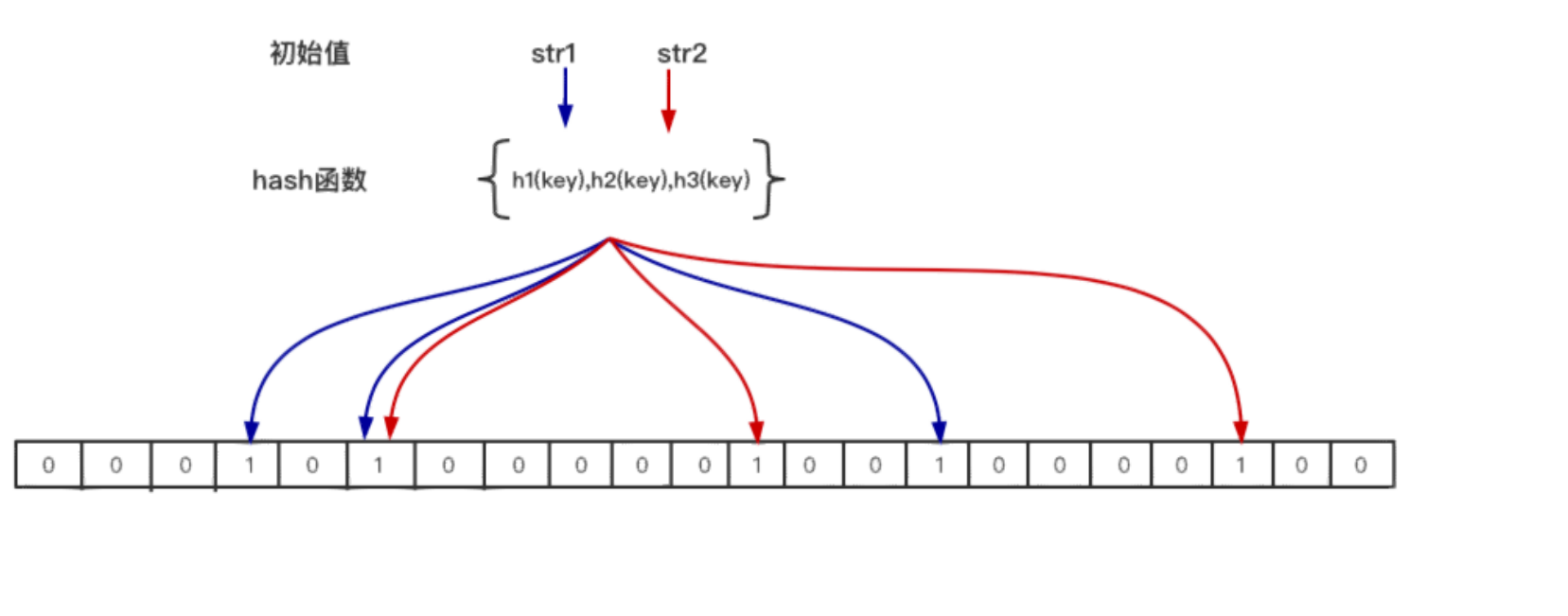
如上图,位图长度未知,有两个key,三个hash函数。这个怎么进行操作的呢?
- 存储:首先将
str1分别依次对三个hash函数进行hash,然后就可以在位图中锁定三个存储位置并相应的置为1。str2也同样的经过三个hash函数得到三个存储位置并相应的置为1。 - 搜索:将key通过三个hash函数进行hash,找到在位图上具体的位置,只要发现其中有一个位置的值为0,则这个key肯定不存在;因为如果key存在,那么所有位置都应该是1。注意,即使所有都为1,不能说明该key一定存在,因为有假阳率。
布隆过滤器可以判断一个key一定不存在,不能判断一个key一定存在。布隆过滤器中的位图大小远远大于要存储的数据。
布隆过滤器的假阳率是可控的,可以通过配置来控制假阳率。
3.4、应用场景
前面介绍了布隆过滤器的原理,除了原理还需要掌握如何利用布隆过滤器解决实际问题。布隆过滤器通常用于判断某个 key 一定不存在的场景,同时允许判断存在时有误差的情况。
常见处理场景:
- 缓存穿透的解决。
- 热 key 限流。
缓存场景:为了减轻数据库(mysql)的访问压力,在server 端与数据库(mysql)之间加入缓存用来存储热点数据。
缓存穿透:server端请求数据时,缓存和数据库都不包含该数据,最终请求压力全部涌向数据库。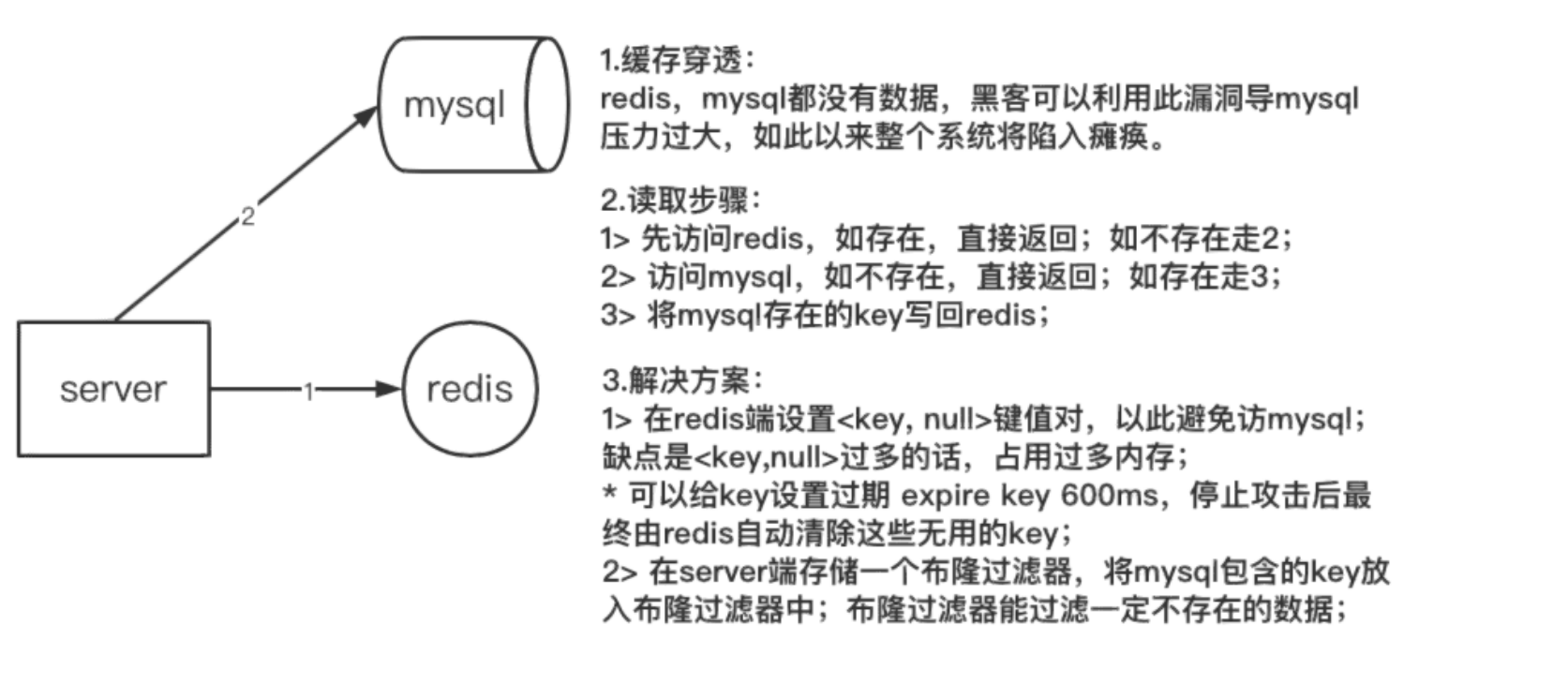
数据请求步骤,如图中 2 所示:
- 先访问redis,如果存在则直接返回,如果不存在则走2访问数据库;
- 访问数据库,如果不存在直接返回,如果存在则将MySQL存在的key写回redis。
发生原因:黑客利用漏洞伪造数据攻击或者内部业务 bug 造成大量重复请求不存在的数据。
解决方案,如图中 3 所示:
- 在redis设置<key,null>键值对,依次避免访问数据库;缺点是<key,null>过多会占用过多内存,可以给key设置过期expire key 600ms,停止攻击后最终由redis自动清除无用的key。
- 在服务端(server)存储一个布隆过滤器,将MySQL存在的key放入布隆过滤器中,布隆过滤器可以过滤一定不存在的数据。
3.5、应用分析
在实际应用中,该选择多少个 hash 函数?要分配多少空间的位图?预期存储多少元素?如何控制误差?
通常有四个参数可以控制布隆过滤器。
- n : 预期布隆过滤器中元素的个数,如上图 只有str1和str2 两元素 那么 n=2。
- p : 假阳率,在0-1之间。
- m: 位图所占空间。
- k : hash函数的个数。
可以使用如下公式计算:
n = ceil(m / (-k / log(1 - exp(log§ / k))))
p = pow(1 - exp(-k / (m / n)), k)
m = ceil((n * log(p)) / log(1 / pow(2, log(2))));
k = round((m / n) * log(2));
这些公式的证明这里就不展开了,这里主要从应用的角度介绍它们。
数学公式:
n
=
⌈
m
÷
(
−
k
÷
log
(
1
−
e
(
log
(
p
)
÷
k
)
)
)
⌉
n=\lceil m\div(-k\div\log(1-e^{(\log(p)\div k))}) \rceil
n=⌈m÷(−k÷log(1−e(log(p)÷k)))⌉
p
=
(
1
−
e
−
k
÷
(
m
÷
n
)
)
k
p=(1-e^{-k\div(m\div n)})^k
p=(1−e−k÷(m÷n))k
m
=
⌈
(
n
×
log
(
p
)
)
÷
log
(
1
÷
2
log
2
)
⌉
m=\lceil (n\times\log(p)) \div \log(1\div 2^{\log2} ) \rceil
m=⌈(n×log(p))÷log(1÷2log2)⌉
r
o
u
n
d
(
(
m
÷
n
)
∗
log
2
)
round((m\div n)*\log2)
round((m÷n)∗log2)
假设:
n = 6000
p = 0.000000001
m = 258797 (31.59KiB)
k = 30
得到如下关系图: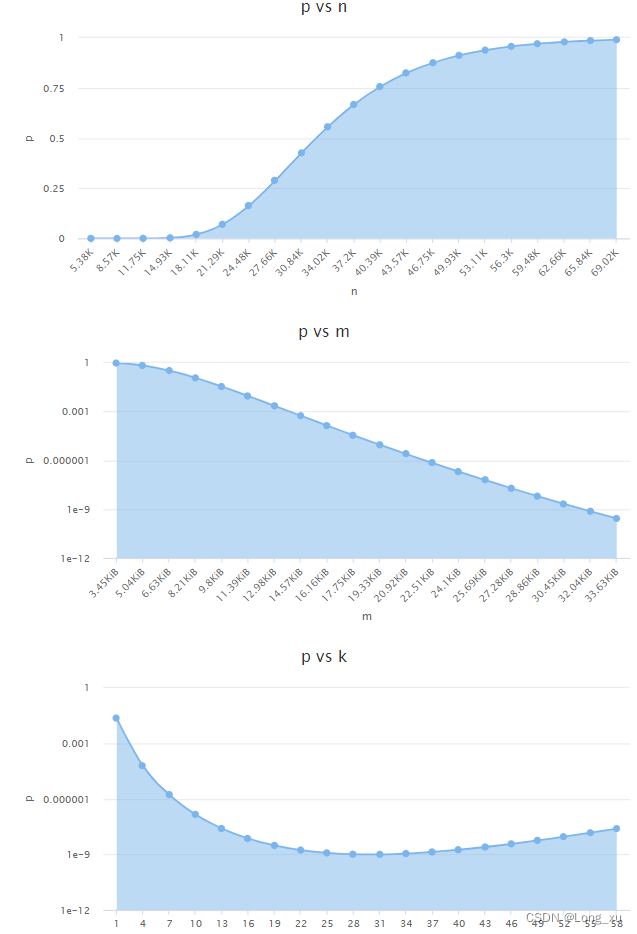
(1)假阳率p会随着插入元素的增多而逐渐变高。
(2)假阳率p会随着位图所占空间的增大而减小。
(3)假阳率p会随着hash函数个数增多,呈现快速减小后缓慢增长的趋势。hash函数个数在31时假阳率最低。这里可以验证一个结论:在hash函数中,在31处出现冲突的概率最低。
在实际使用布隆过滤器时,首先需要确定 n 和 p,通过上面的运算得出 m 和 k;推荐一个布隆过滤器计算器可以选出合适的值。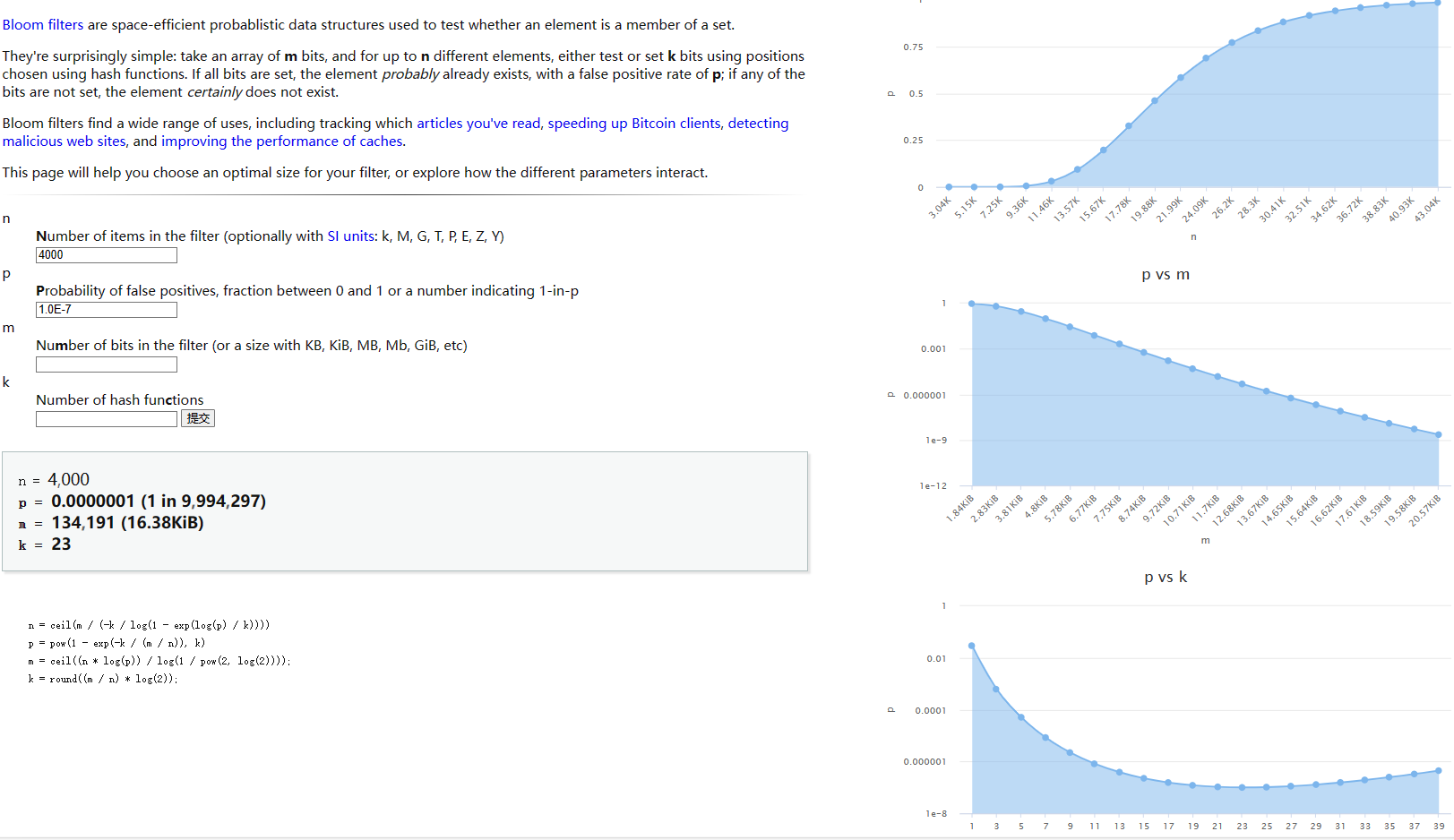
选择hash函数:
选择一个 hash 函数,通过给 hash 传递不同的种子偏移值,采用线性探寻的方式构造多个 hash 函数。
#defineMIX_UINT64(v)((uint32_t)((v>>32)^(v)))uint64_t hash1 =MurmurHash2_x64(key, len, Seed);uint64_t hash2 =MurmurHash2_x64(key, len,MIX_UINT64(hash1));for(i =0; i < k; i++)// k 是hash函数的个数{
Pos[i]=(hash1 + i*hash2)% m;// m 是位图的⼤⼩}
所谓不同的hash函数主要是seed不一样创造出来的。在实际应用中会有一个seed表,用于不断的计算偏移值。每次生成hash函数的时候会把seed值修改,通过不同的数值运算来得到hash函数。在使用过程中会先填充一个随机种子,然后进行偏移计算,最终得到所需的hash函数。
3.6、布隆过滤器的实际使用
为了避免篇幅过长,代码已经上传到gitee,感兴趣可以点击了解。里面包含布隆过滤器的实现源码和三个使用示例。
布隆过滤器的接口分为两个部分:
- 计算所需的四个参数:n、p、m、k;主要是根据n、和p计算出m和k。利用一个类封装好,包含计算m、k的值。
- 布隆过滤器。会准备一个位图,实现插入元素的接口,定义hash函数的最大个数,确定布隆过滤器的长度,预期插入元素的个数,已经插入元素的个数,seed随机值,具体的假阳率等等。
使用过程:先插入,然后contain。
3.7、小结
布隆过滤器的特征:
- 能确定一个key一定不存在,可控假阳率确定存在。
- 不能删除。可以通过准备两个布隆过滤器来解决删除时也降低假阳率,添加放在第一个布隆过滤器,删除放在第二个布隆过滤器。判断key是否存在时先判断key是否在第二个布隆过滤器(目的是检查之前是否删除过该key),如果之前删除过该key,就可以将该key加入第一个布隆过滤器。
- 使用过程中根据n和p计算出m和k。hash函数的生成使用开放寻址法进行。
思维导图:
四、分布式一致性hash
分布式一致性hash主要解决分布式缓存中的扩容问题。
4.1、背景
假设一个服务器,只有一个缓存结点,当存储的数据越来越多时,效率就越来越低,这时就需要增加结点进行分流分压。那么如何实现优雅的扩容(数据随机、均匀分布)?首先想到使用hash方法解决,但扩容时(增加结点)会出现算法改变;比如原来有n个结点,key通过hash(key)%n确定存储在哪个结点,现在添加新的结点变成了n+1,key通过hash(key)%(n+1)寻找存储结点就会出现缓存失效。
#mermaid-svg-gibdoiCo4e9wc9uU {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-gibdoiCo4e9wc9uU .error-icon{fill:#552222;}#mermaid-svg-gibdoiCo4e9wc9uU .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-gibdoiCo4e9wc9uU .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-gibdoiCo4e9wc9uU .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-gibdoiCo4e9wc9uU .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-gibdoiCo4e9wc9uU .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-gibdoiCo4e9wc9uU .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-gibdoiCo4e9wc9uU .marker{fill:#333333;stroke:#333333;}#mermaid-svg-gibdoiCo4e9wc9uU .marker.cross{stroke:#333333;}#mermaid-svg-gibdoiCo4e9wc9uU svg{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-gibdoiCo4e9wc9uU .label{font-family:"trebuchet ms",verdana,arial,sans-serif;color:#333;}#mermaid-svg-gibdoiCo4e9wc9uU .cluster-label text{fill:#333;}#mermaid-svg-gibdoiCo4e9wc9uU .cluster-label span{color:#333;}#mermaid-svg-gibdoiCo4e9wc9uU .label text,#mermaid-svg-gibdoiCo4e9wc9uU span{fill:#333;color:#333;}#mermaid-svg-gibdoiCo4e9wc9uU .node rect,#mermaid-svg-gibdoiCo4e9wc9uU .node circle,#mermaid-svg-gibdoiCo4e9wc9uU .node ellipse,#mermaid-svg-gibdoiCo4e9wc9uU .node polygon,#mermaid-svg-gibdoiCo4e9wc9uU .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-gibdoiCo4e9wc9uU .node .label{text-align:center;}#mermaid-svg-gibdoiCo4e9wc9uU .node.clickable{cursor:pointer;}#mermaid-svg-gibdoiCo4e9wc9uU .arrowheadPath{fill:#333333;}#mermaid-svg-gibdoiCo4e9wc9uU .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-gibdoiCo4e9wc9uU .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-gibdoiCo4e9wc9uU .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-gibdoiCo4e9wc9uU .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-gibdoiCo4e9wc9uU .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-gibdoiCo4e9wc9uU .cluster text{fill:#333;}#mermaid-svg-gibdoiCo4e9wc9uU .cluster span{color:#333;}#mermaid-svg-gibdoiCo4e9wc9uU div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-gibdoiCo4e9wc9uU :root{--mermaid-font-family:"trebuchet ms",verdana,arial,sans-serif;}
扩容
扩容n=4
缓存失效
缓存失效
1号结点
2号结点
3号结点
0号结点
hash(key=1)%4=1
hash(key=2)%4=2
hash(key=3)%4=3
hash(key=4)%4=0
现在n=3
1号结点
2号结点
0号结点
hash(key=1)%3=1
hash(key=2)%3=2
hash(key=3)%3=0
hash(key=4)%3=1
分布式一致性hash就解决了缓存扩容的问题。为解决缓存失效,首先会固定算法;然后改变查找节点的映射关系。
分布式一致性hash算法将hash空间组织成一个虚拟的圆环,圆环大小为
2
32
2^{32}
232 。
算法为:hash(ip) %
2
32
2^{32}
232,最终会得到一个 [0,
2
32
−
1
2^{32}-1
232−1] 之间的一个无符号整型,这个整数代表服务器的编号;多个服务器都通过这种方式在 hash 环上映射一个点来标识该服务器的位置;当用户操作某个 key,通过同样的算法生成一个值,沿环顺时针定位某个服务器,那么该 key 就在该服务器中。
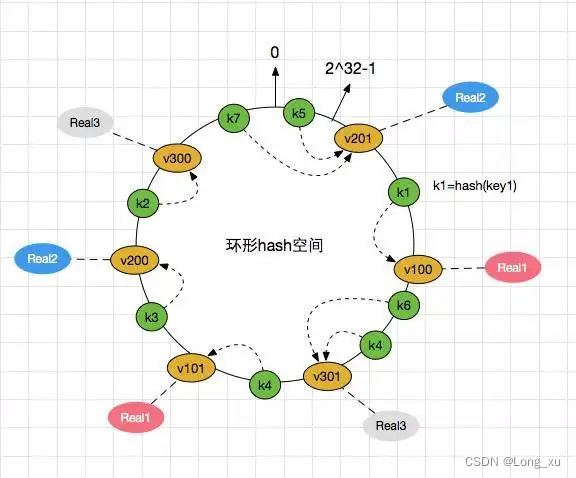
4.2、一致性hash原理
(1)映射空间可抽象为一个环,长度为
2
32
2^{32}
232,范围为[0,
2
32
−
1
2^{32}-1
232−1],每个服务器节点根据自己的哈希值被映射到这个环上;
(2)判断一条数据属于哪个服务器节点的方法:根据数据的哈希值,去哈希环找到第一个大于等于数据哈希值的机器(可以理解为离它最近)。如果数据的哈希值大于当前最大的机器哈希值,那么就把这个数据放在位置最靠前(哈希值最小)的机器上,因为是一个环。
(3)为了解决实际机器过少导致的数据倾斜问题(例如目前一共3个机器,机器A、B的哈希值分别为1和2,而另一个机器C的哈希值为 2^32-1,那么大部分的数据都会被分给机器C),引入了虚拟节点概念,虚拟节点相当于真实节点的分身,一个真实节点可以有很多个虚拟节点,当数据被分配给这些虚拟节点时,本质上是分给这个真实节点的。由于数量变多了,数据分布的均衡性会有所提高;
(4)新增节点时:例如原本的节点哈希值列表为[1,100,500,1000],新增节点800后,在501~799范围内的数据原本是分给哈希值为1000的节点的,现在要把这部分数据迁移到节点800;
(5)删除节点:例如原本的节点哈希值列表为[1,100,500,800,1000],删除节点500后,原本范围是101~500的数据要迁移到节点800.
4.3、应用场景
(1)分布式缓存;将数据均衡地分散在不同的服务器当中,用来分摊缓存服务器的压力;
(2)解决缓存服务器数量变化尽量不影响缓存失效.
4.4、hash偏移
hash算法得到的结果是随机的,不能保证服务器节点均匀分布在hash环上;分布不均造成请求访问不均匀,服务器承受的压力不均匀。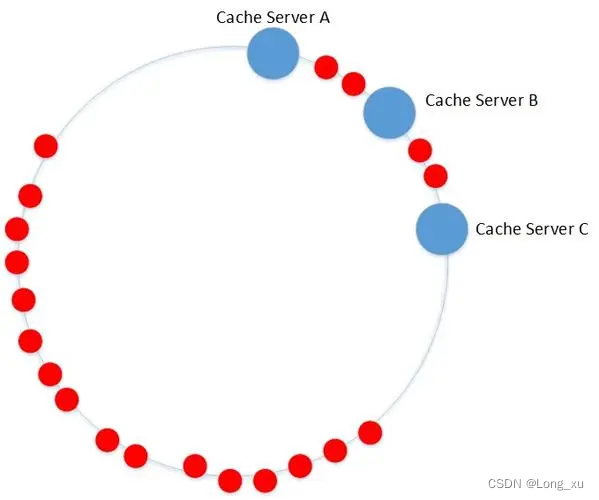
为了解决实际机器过少导致的数据倾斜问题(例如目前一共3个机器,机器A、B的哈希值分别为1和2,而另一个机器C的哈希值为 2^32-1,那么大部分的数据都会被分给机器C),引入了虚拟节点概念,虚拟节点相当于真实节点的分身,一个真实节点可以有很多个虚拟节点,当数据被分配给这些虚拟节点时,本质上是分给这个真实节点的。由于数量变多了,数据分布的均衡性会有所提高;
4.5、hash迁移
新增节点时,例如原本的节点哈希值列表为[1,100,500,1000],新增节点800后,在501~799范围内的数据原本是分给哈希值为1000的节点的,现在要把这部分数据迁移到节点800。
4.6、虚拟结点
为了解决哈希偏移的问题,增加了虚拟节点的概念;理论上,哈希环上节点数越多,数据分布越均衡;为每个服务节点计算多个哈希节点(虚拟节点);通常做法
是,hash(“IP:PORT:seqno”) %
2
32
2^{32}
232。
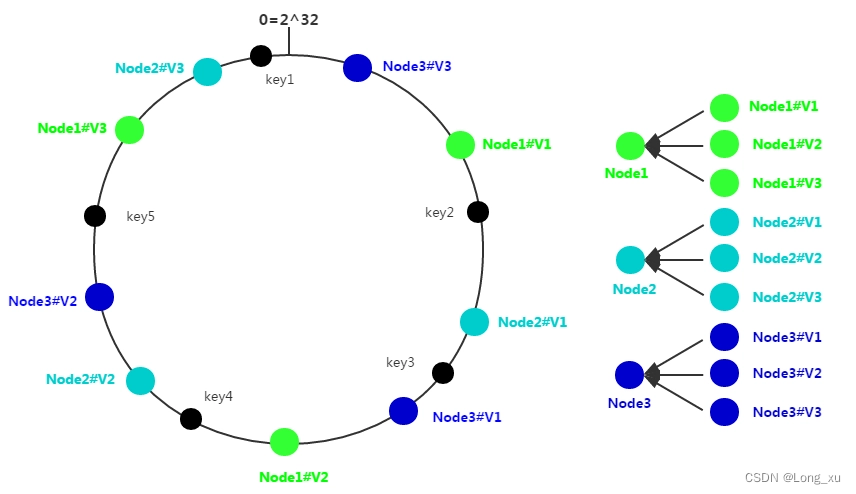
添加虚拟节点解决了哈希偏移的问题,同时使hash迁移的数据量变小;这对工程应用来说是非常重要的,因为在做数据迁移的过程中,整个系统是不能提供服务的。
4.7、思维导图

五、思考
(1)只用 2GB 内存在 20 亿个整数中找到出现次数最多的数?
关键点,内存有限、海量数据、次数最多。要找出现次数最多,那么就一定要统计,使用key-value键值对,key保存整数,value保存出现次数。统计可以使用散列表来解决。
对于key-value键值对,key是整数占4字节,如果按照最坏情况(即1个整数出现20 亿次),value可以使用uint32存储(uint32可达21亿多,刚好能存储下20亿),uint32也是占4字节;因此一个key-value对占8个字节。如果要在内存中处理20亿个数据就需要
2000000000
×
8
=
16
G
B
2000000000 \times 8=16 GB
2000000000×8=16GB内存,超出2GB内存的限制。
要在有限内存里处理,可以采用拆分的思维,将20亿拆分成若干等份。那么采用什么策略来拆分?首先要清楚,20亿的数据是散列分布的,不能采用等分的方式,我们的目的要把相同的整数放在同一个文件中,hash函数可以实现这个目的(相同的key经过hash得到的值总是相同)。
一个hash函数两个用途,一方面是对数据拆分将相同整数放入同一个文件或等份,另一方面将其应用到散列表中(散列表的存储数据取余)。hash函数具有强随机性,数据属于海量数据,那么数据拆分多少份?可以计算最差情况需要拆分多少份和最好的情况需要拆分多少份,如果随机性不能达到预期,再增加份数。
比如,将20亿拆分为10份(如果不能达到预期的随机性再增大),平均的情况是每份2亿,具体情况再具体调整。
#mermaid-svg-vUXDic2iVYQ2seNM {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-vUXDic2iVYQ2seNM .error-icon{fill:#552222;}#mermaid-svg-vUXDic2iVYQ2seNM .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-vUXDic2iVYQ2seNM .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-vUXDic2iVYQ2seNM .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-vUXDic2iVYQ2seNM .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-vUXDic2iVYQ2seNM .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-vUXDic2iVYQ2seNM .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-vUXDic2iVYQ2seNM .marker{fill:#333333;stroke:#333333;}#mermaid-svg-vUXDic2iVYQ2seNM .marker.cross{stroke:#333333;}#mermaid-svg-vUXDic2iVYQ2seNM svg{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-vUXDic2iVYQ2seNM .label{font-family:"trebuchet ms",verdana,arial,sans-serif;color:#333;}#mermaid-svg-vUXDic2iVYQ2seNM .cluster-label text{fill:#333;}#mermaid-svg-vUXDic2iVYQ2seNM .cluster-label span{color:#333;}#mermaid-svg-vUXDic2iVYQ2seNM .label text,#mermaid-svg-vUXDic2iVYQ2seNM span{fill:#333;color:#333;}#mermaid-svg-vUXDic2iVYQ2seNM .node rect,#mermaid-svg-vUXDic2iVYQ2seNM .node circle,#mermaid-svg-vUXDic2iVYQ2seNM .node ellipse,#mermaid-svg-vUXDic2iVYQ2seNM .node polygon,#mermaid-svg-vUXDic2iVYQ2seNM .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-vUXDic2iVYQ2seNM .node .label{text-align:center;}#mermaid-svg-vUXDic2iVYQ2seNM .node.clickable{cursor:pointer;}#mermaid-svg-vUXDic2iVYQ2seNM .arrowheadPath{fill:#333333;}#mermaid-svg-vUXDic2iVYQ2seNM .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-vUXDic2iVYQ2seNM .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-vUXDic2iVYQ2seNM .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-vUXDic2iVYQ2seNM .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-vUXDic2iVYQ2seNM .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-vUXDic2iVYQ2seNM .cluster text{fill:#333;}#mermaid-svg-vUXDic2iVYQ2seNM .cluster span{color:#333;}#mermaid-svg-vUXDic2iVYQ2seNM div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-vUXDic2iVYQ2seNM :root{--mermaid-font-family:"trebuchet ms",verdana,arial,sans-serif;}
key
key
拆分
0
1
2
3
4
5
6
7
8
9
20 亿个整数
hash(key) % 10
hash(key) % array_size
散列表
总结
hash的应用:
#mermaid-svg-IFwhS0Q1RvrtdIwb {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-IFwhS0Q1RvrtdIwb .error-icon{fill:#552222;}#mermaid-svg-IFwhS0Q1RvrtdIwb .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-IFwhS0Q1RvrtdIwb .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-IFwhS0Q1RvrtdIwb .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-IFwhS0Q1RvrtdIwb .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-IFwhS0Q1RvrtdIwb .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-IFwhS0Q1RvrtdIwb .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-IFwhS0Q1RvrtdIwb .marker{fill:#333333;stroke:#333333;}#mermaid-svg-IFwhS0Q1RvrtdIwb .marker.cross{stroke:#333333;}#mermaid-svg-IFwhS0Q1RvrtdIwb svg{font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-IFwhS0Q1RvrtdIwb .label{font-family:"trebuchet ms",verdana,arial,sans-serif;color:#333;}#mermaid-svg-IFwhS0Q1RvrtdIwb .cluster-label text{fill:#333;}#mermaid-svg-IFwhS0Q1RvrtdIwb .cluster-label span{color:#333;}#mermaid-svg-IFwhS0Q1RvrtdIwb .label text,#mermaid-svg-IFwhS0Q1RvrtdIwb span{fill:#333;color:#333;}#mermaid-svg-IFwhS0Q1RvrtdIwb .node rect,#mermaid-svg-IFwhS0Q1RvrtdIwb .node circle,#mermaid-svg-IFwhS0Q1RvrtdIwb .node ellipse,#mermaid-svg-IFwhS0Q1RvrtdIwb .node polygon,#mermaid-svg-IFwhS0Q1RvrtdIwb .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-IFwhS0Q1RvrtdIwb .node .label{text-align:center;}#mermaid-svg-IFwhS0Q1RvrtdIwb .node.clickable{cursor:pointer;}#mermaid-svg-IFwhS0Q1RvrtdIwb .arrowheadPath{fill:#333333;}#mermaid-svg-IFwhS0Q1RvrtdIwb .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-IFwhS0Q1RvrtdIwb .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-IFwhS0Q1RvrtdIwb .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-IFwhS0Q1RvrtdIwb .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-IFwhS0Q1RvrtdIwb .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-IFwhS0Q1RvrtdIwb .cluster text{fill:#333;}#mermaid-svg-IFwhS0Q1RvrtdIwb .cluster span{color:#333;}#mermaid-svg-IFwhS0Q1RvrtdIwb div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-IFwhS0Q1RvrtdIwb :root{--mermaid-font-family:"trebuchet ms",verdana,arial,sans-serif;}
hash
hash函数以及冲突处理
散列表, 也称为哈希表
应用: STL中的unordered_map
布隆过滤器
应用: MySQL缓存方案
应用: rocksdb中的数据查找
应用: hyperloglog, redis的数据结构
分布式一致性hash
应用: redis cluster集群
分布式一致性hash算法通过固定算法,改变查找结点的映射关系,数据迁移,避免缓存失效,解决分布式扩容的问题;通过虚拟节点的方式保证数据均衡。
在大数据中,涉及到大文件或海量数据的,解决方案都是通过hash将大文件拆分为小文件;涉及单台机器无法承受或处理不过来的问题,解决方案都是通过hash分流到多台机器;选择hash的原因是利用其强随机分布的特性,以及把相同的数据分配到相同的位置。
版权归原作者 Lion Long 所有, 如有侵权,请联系我们删除。