完整题目:
链接:https://pan.baidu.com/s/16E1X35O13NWIij72OClVgQ?pwd=1234
提取码:1234
文章目录
一、题目

二、问题分析
三、模型假设
1.用于组装小组件的材料充足。
2.生产过程中,不会因为工厂停电、机械故障等突发情况打断生产。
3.工厂资金流正常,不会因为缺乏资金而影响生产。
4.只有最终产品机器人有外部需求,其他组件不对外销售。
5.机器人的需求按计划而定,不受市场价格波动的影响。
四、符号说明
符号说明单位d第几天天MA1d , MA2d ,MA3d … MC3d小组件第d天的组装数量个SA1d , SA2d ,SA3d … SC3d小组件第d天的剩余数量个MAd , MBd ,MCd大组件第d天的组装数量个SAd , SBd ,SCd大组件第d天的剩余数量个DWd机器人第d天的需求数量个MWd机器人第d天的组装数量个SWd机器人第d天的剩余数量个Td第d天总工时限制工时RA1,RA2,…RB,RC该组件的单件存储费用元FA1,FA2,…,FB,FC该组件的生产准备费用元XWd第d天是否生产机器人的0-1变量-Rd第d天的库存费用元Fd第d天的生产准备费用元checkDatet第t次检修的日期天Tbigd第d天总工时限制工时DWpredictd未来某周第d天机器人的需求数量个
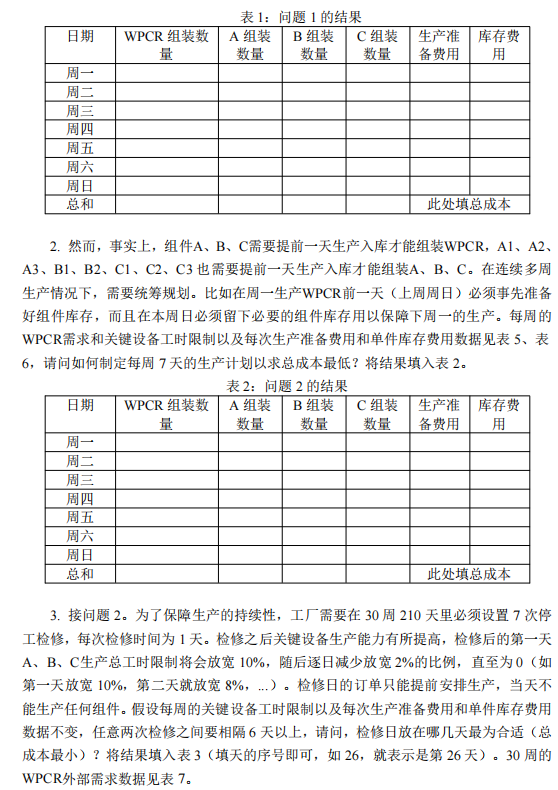
五、问题一模型的建立与求解
5.1 问题一模型的建立
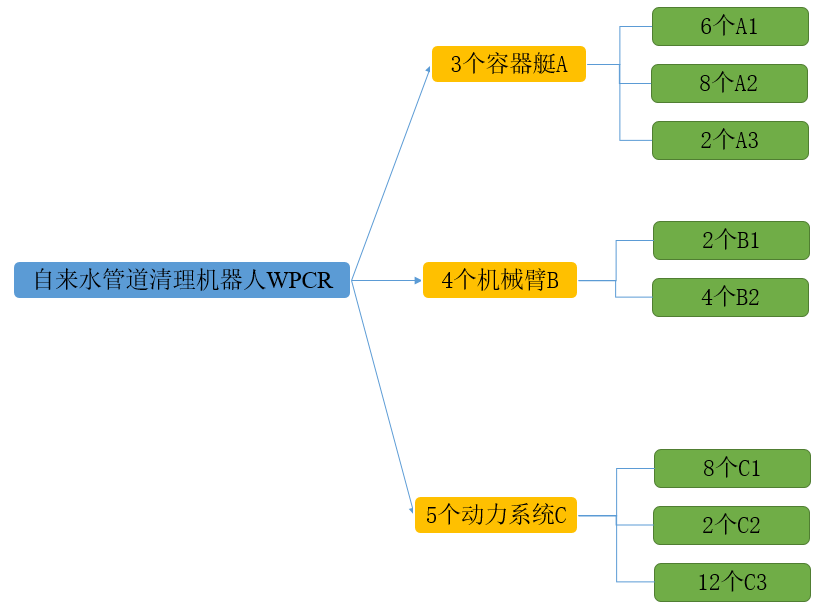
5.1.1 小组件组装大组件
此处以组装大组件A为例。组装一个大组件A,需要6个小组件A1,8个小组件A2,2个小组件A3。
在第d天时,用于组装大组件A的小组件A1数量是:第d天(当天)组装的小组件数量 MA1d和第d-1天(昨天)剩余的小组件数量SA1d-1之和,即MA1d+SA1d-1。小组件A2、A3的数量同理可得。
组装一个大组件A需要6个小组件A1,若只考虑A1,则最多可以组装大组件的数量为:
[
M
A
1
d
+
S
A
1
d
−
1
6
]
(1)
\left[ \begin{matrix} \frac{MA1_d+SA1_{d-1}}{6} \end{matrix} \right] \tag{1}
[6MA1d+SA1d−1](1)
注:此处符号[ ]为向下取整,即取比自己小的最大整数。
同理,若只考虑A2,则最多可以组装大组件A的数量为:
[
M
A
2
d
+
S
A
2
d
−
1
8
]
(2)
\left[ \begin{matrix} \frac{MA2_d+SA2_{d-1}}{8} \end{matrix} \right] \tag{2}
[8MA2d+SA2d−1](2)
若只考虑A3,则最多可以组装大组件A的数量为:
[
M
A
3
d
+
S
A
3
d
−
1
2
]
(3)
\left[ \begin{matrix} \frac{MA3_d+SA3_{d-1}}{2} \end{matrix} \right] \tag{3}
[2MA3d+SA3d−1](3)
因此,第d天大组件A的组装数量的最大值为:
m
i
n
[
(
M
A
1
d
+
S
A
1
d
−
1
6
,
M
A
2
d
+
S
A
2
d
−
1
8
,
M
A
3
d
+
S
A
3
d
−
1
2
)
]
(4)
min\left[ \begin{pmatrix} \frac{MA1_d+SA1_{d-1}}{6}, \frac{MA2_d+SA2_{d-1}}{8}, \frac{MA3_d+SA3_{d-1}}{2} \end{pmatrix} \right]\tag{4}
min[(6MA1d+SA1d−1,8MA2d+SA2d−1,2MA3d+SA3d−1)](4)
注:这里需要向下取整
每天机器人的需求数量是不同的,再满足订单的需求下,工厂组装大组件A时,并不一定要等于该最大值。因此,在第d天,大组件A的组装数量应当满足如下约束条件:
M
A
d
⩽
m
i
n
[
(
M
A
1
d
+
S
A
1
d
−
1
6
,
M
A
2
d
+
S
A
2
d
−
1
8
,
M
A
3
d
+
S
A
3
d
−
1
2
)
]
(5)
MA_d \leqslant min\left[ \begin{pmatrix} \frac{MA1_d+SA1_{d-1}}{6}, \frac{MA2_d+SA2_{d-1}}{8}, \frac{MA3_d+SA3_{d-1}}{2} \end{pmatrix} \right]\tag{5}
MAd⩽min[(6MA1d+SA1d−1,8MA2d+SA2d−1,2MA3d+SA3d−1)](5)
同理可得,在第d天,大组件B,C的组装数量应当满足如下约束条件:
M
B
d
⩽
m
i
n
[
(
M
B
1
d
+
S
B
1
d
−
1
2
,
M
B
2
d
+
S
B
2
d
−
1
4
,
)
]
(6)
MB_d \leqslant min\left[ \begin{pmatrix} \frac{MB1_d+SB1_{d-1}}{2}, \frac{MB2_d+SB2_{d-1}}{4}, \end{pmatrix} \right]\tag{6}
MBd⩽min[(2MB1d+SB1d−1,4MB2d+SB2d−1,)](6)
M
C
d
⩽
m
i
n
[
(
M
C
1
d
+
S
C
1
d
−
1
8
,
M
C
2
d
+
S
C
2
d
−
1
2
,
M
C
2
d
+
S
C
2
d
−
1
12
)
]
(6)
MC_d \leqslant min\left[ \begin{pmatrix} \frac{MC1_d+SC1_{d-1}}{8}, \frac{MC2_d+SC2_{d-1}}{2}, \frac{MC2_d+SC2_{d-1}}{12} \end{pmatrix} \right]\tag{6}
MCd⩽min[(8MC1d+SC1d−1,2MC2d+SC2d−1,12MC2d+SC2d−1)](6)
5.1.2 小组件的剩余
用小组件组装大组件后,小组件有可能会有剩余。此处以小组件A1为例。
在第d天,小组件A1的剩余数量,应当满足,第d天组装的小组件数量MA1d,和第d-1天剩余的小组件数量SA1d-1之和,减去第d天对Al的消耗数量。组装一个大组件A,需要6个小组件A1。因此,第d天Al的消耗数量为6×MAd。故第d天A1的剩余数量SA1d如下所示:
S
A
1
d
=
M
A
1
d
+
S
A
1
d
−
1
−
6
∗
M
A
d
(7)
SA1_d=MA1_d+SA1_{d-1} -6*MA_d \tag{7}
SA1d=MA1d+SA1d−1−6∗MAd(7)
今天有的-消耗的=剩下的
(今天组装的+昨天剩下的)-消耗的=剩下的
其他小组件的剩余数量同理可得:
S
A
2
d
=
M
A
2
d
+
S
A
2
d
−
1
−
8
∗
M
A
d
SA2_d=MA2_d+SA2_{d-1} -8*MA_d
SA2d=MA2d+SA2d−1−8∗MAd
S
A
3
d
=
M
A
3
d
+
S
A
3
d
−
1
−
2
∗
M
A
d
SA3_d=MA3_d+SA3_{d-1} -2*MA_d
SA3d=MA3d+SA3d−1−2∗MAd
S
B
1
d
=
M
B
1
d
+
S
B
1
d
−
1
−
2
∗
M
B
d
SB1_d=MB1_d+SB1_{d-1} -2*MB_d
SB1d=MB1d+SB1d−1−2∗MBd
S
B
2
d
=
M
A
1
d
+
S
A
1
d
−
1
−
4
∗
M
B
d
(8)
SB2_d=MA1_d+SA1_{d-1} -4*MB_d \tag{8}
SB2d=MA1d+SA1d−1−4∗MBd(8)
S
C
1
d
=
M
C
1
d
+
S
C
1
d
−
1
−
8
∗
M
C
d
SC1_d=MC1_d+SC1_{d-1} -8*MC_d
SC1d=MC1d+SC1d−1−8∗MCd
S
C
2
d
=
M
C
2
d
+
S
C
2
d
−
1
−
2
∗
M
C
d
SC2_d=MC2_d+SC2_{d-1} -2*MC_d
SC2d=MC2d+SC2d−1−2∗MCd
S
C
3
d
=
M
C
3
d
+
S
C
3
d
−
1
−
12
∗
M
C
d
SC3_d=MC3_d+SC3_{d-1} -12*MC_d
SC3d=MC3d+SC3d−1−12∗MCd
5.1.3 机器人的组装数量计算 大组件剩余
机器人的组装,即用大组件组装机器人,与用小组件组装大组件同理,因此第d天机器人的组装数量如下:
M
W
d
⩽
m
i
n
[
(
M
A
1
d
+
S
A
1
d
−
1
3
,
M
B
2
d
+
S
B
2
d
−
1
4
,
M
C
2
d
+
S
C
2
d
−
1
5
)
]
(9)
MW_d \leqslant min\left[ \begin{pmatrix} \frac{MA1_d+SA1_{d-1}}{3}, \frac{MB2_d+SB2_{d-1}}{4}, \frac{MC2_d+SC2_{d-1}}{5} \end{pmatrix} \right]\tag{9}
MWd⩽min[(3MA1d+SA1d−1,4MB2d+SB2d−1,5MC2d+SC2d−1)](9)
其中,MWd 为机器人组装数量,MAd 为第d天大组件A的组装数量,SAd-1 为第d-1天大组件A的剩余数量。
用大组件组装机器人,大组件可能会有所剩余。其计算方法与计算小组件的剩余数量同理,如下所示:
S
A
d
=
M
A
d
+
S
A
d
−
1
−
3
∗
M
W
d
SA_d=MA_d+SA_{d-1} -3*MW_d
SAd=MAd+SAd−1−3∗MWd
S
B
d
=
M
B
d
+
S
B
d
−
1
−
4
∗
M
W
d
(10)
SB_d=MB_d+SB_{d-1} -4*MW_d \tag{10}
SBd=MBd+SBd−1−4∗MWd(10)
S
C
d
=
M
C
d
+
S
C
d
−
1
−
5
∗
M
W
d
SC_d=MC_d+SC_{d-1} -5*MW_d
SCd=MCd+SCd−1−5∗MWd
5.1.4 机器人组装数量约束
工厂接受的机器人需求的所有订单到期必须全部交货,因此第d天机器人的组装数量MWd与第d-1天机器人的剩余数量SWd之和,应大于第d天的需求量DWd。
M
W
d
+
S
W
d
−
1
⩾
D
W
d
(12)
MW_d+SW_{d-1} \geqslant DW_d \tag{12}
MWd+SWd−1⩾DWd(12)
5.1.5 机器人剩余
每日按订单销售机器人后,可能会有所剩余。第d天机器人的剩余SWd 等于第d天组装数量MWd 与第d-1天的剩余量SWd-1 之和减去当天的订单数量DWd 。即
S
W
d
=
M
W
d
+
S
W
d
−
1
−
D
W
d
(12)
SW_d=MW_d+SW_{d-1} -DW_d \tag{12}
SWd=MWd+SWd−1−DWd(12)
5.1.6 没有库存 没有剩余
第一天开始时没有任何组件库存,即:
S
A
1
0
=
S
A
2
0
=
S
A
3
0
=
S
B
1
0
=
S
B
2
0
=
S
C
1
0
=
S
C
2
0
=
S
C
3
0
(13)
SA1_0=SA2_0=SA3_0=SB1_0=SB2_0=SC1_0=SC2_0=SC3_0 \tag{13}
SA10=SA20=SA30=SB10=SB20=SC10=SC20=SC30(13)
S
A
0
=
S
B
0
=
S
C
0
=
0
(13)
SA_0=SB_0=SC_0=0 \tag{13}
SA0=SB0=SC0=0(13)
第七天结束后不会留下任何组件库存,即
S
A
1
7
=
S
A
2
7
=
S
A
3
7
=
S
B
1
7
=
S
B
2
7
=
S
C
1
7
=
S
C
2
7
=
S
C
3
7
SA1_7=SA2_7=SA3_7=SB1_7=SB2_7=SC1_7=SC2_7=SC3_7
SA17=SA27=SA37=SB17=SB27=SC17=SC27=SC37
S
A
7
=
S
B
7
=
S
C
7
=
0
(14)
SA_7=SB_7=SC_7=0 \tag{14}
SA7=SB7=SC7=0(14)
S
W
7
=
0
SW_7=0
SW7=0
5.1.7 工时的限制
生产1件A需要占用3个工时,生产1件B需要占用5个工时,生产1件C需要占用5个工时。一次需要满足如下约束条件:
3
×
M
A
d
+
5
×
M
B
d
+
5
×
M
C
d
⩽
T
d
(15)
3\times MA_d+5\times MB_d+5\times MC_d \leqslant T_d \tag{15}
3×MAd+5×MBd+5×MCd⩽Td(15)
5.1.8 库存费用
某一天结束时某组件有库存在,则工厂必须付出一定的库存费用,而库存费用与组件的剩余数量成正比。因此,根据第d天组件的剩余数量,即可表示出小组件,大组件,机器人的库存费用。
R
s
m
a
l
l
A
d
=
R
A
1
×
S
A
1
d
+
R
A
2
×
S
A
2
d
+
R
A
3
×
S
A
3
d
RsmallA_d =RA1\times SA1_d+RA2\times SA2_d+RA3\times SA3_d
RsmallAd=RA1×SA1d+RA2×SA2d+RA3×SA3d
R
s
m
a
l
l
B
d
=
R
B
1
×
S
B
1
d
+
R
B
2
×
S
B
2
d
RsmallB_d =RB1\times SB1_d+RB2\times SB2_d
RsmallBd=RB1×SB1d+RB2×SB2d
R
s
m
a
l
l
C
d
=
R
C
1
×
S
C
1
d
+
R
C
2
×
S
C
2
d
+
R
C
3
×
S
C
3
d
(16)
RsmallC_d =RC1\times SC1_d+RC2\times SC2_d+RC3\times SC3_d \tag{16}
RsmallCd=RC1×SC1d+RC2×SC2d+RC3×SC3d(16)
R
b
i
g
d
=
R
A
×
S
A
d
+
R
B
×
S
B
d
+
R
C
×
S
C
d
Rbig_d =RA\times SA_d+RB\times SB_d+RC\times SC_d
Rbigd=RA×SAd+RB×SBd+RC×SCd
其中,RA1为大组件A的单件库存费用,SA1d为大组件A第d天的剩余数量。其他符号同理。RsmallAd、RsmallBd、RsmallCd为小组件A、B、C第d天的库存费用,Rbig大组件第d天的库存费用,Rd为第d天的总库存费用。
求和即为第d天的库存费用:
R
d
=
R
s
m
a
l
l
A
d
+
R
s
m
a
l
l
B
d
+
R
s
m
a
l
l
C
d
+
R
b
i
g
d
+
R
W
×
S
W
d
(17)
R_d =RsmallA_d+RsmallB_d+RsmallC_d+Rbig_d+RW\times SW_d \tag{17}
Rd=RsmallAd+RsmallBd+RsmallCd+Rbigd+RW×SWd(17)
5.1.9 生产准备费用
工厂在生产组件产品时,需要付出一个与生产数量无关的固定成本,称为生产准备费用,为了便于计算固定成本,此处引入0-1变量。以生产机器人的0-1变量XWd为例。若第d天生产了机器人,则XWd为1;若第d天没有生产机器人,则XWd为0。如下所示
X
W
d
=
{
1
M
W
d
>
0
0
M
W
d
=
0
(18)
XW_d=\begin{cases} 1 & MW_d>0 \\ 0 & MW_d=0 \\ \end{cases}\tag{18}
XWd={10MWd>0MWd=0(18)
其他组件的0-1变量同理可得。
因此,根据所有组件的0-1变量,即可表示出小组件、大组件、机器人的生产准备费用。
F
s
m
a
l
l
A
d
=
X
A
1
d
×
F
A
1
+
X
A
2
d
×
F
A
2
+
X
A
3
d
×
F
A
3
FsmallA_d =XA1_d \times FA1+XA2_d \times FA2+XA3_d \times FA3
FsmallAd=XA1d×FA1+XA2d×FA2+XA3d×FA3
F
s
m
a
l
l
B
d
=
X
B
1
d
×
F
B
1
+
X
B
2
d
×
F
B
2
FsmallB_d =XB1_d \times FB1+XB2_d \times FB2
FsmallBd=XB1d×FB1+XB2d×FB2
F
s
m
a
l
l
C
d
=
X
C
1
d
×
F
C
1
+
X
C
2
d
×
F
C
2
+
X
C
3
d
×
F
C
3
(19)
FsmallC_d =XC1_d \times FC1+XC2_d \times FC2+XC3_d \times FC3 \tag{19}
FsmallCd=XC1d×FC1+XC2d×FC2+XC3d×FC3(19)
F
b
i
g
d
=
F
A
×
X
A
d
+
F
B
×
X
B
d
+
F
C
×
X
C
d
Fbig_d =FA\times XA_d+FB\times XB_d+FC\times XC_d
Fbigd=FA×XAd+FB×XBd+FC×XCd
其中,XA1d为第d天的是否生产A1的0-1变量,FA1为Al的生产准备费用。
其他符号同理。FsmallAd、FsmallBd、FsmallCd为小组件A、B、C第d天的生产准备费用,Fbig大组件第d天的库存费用。Fd为第d天的生产准备费用费用。
求和即为第d天的生产准备费用:
F
d
=
F
s
m
a
l
l
A
d
+
F
s
m
a
l
l
B
d
+
F
s
m
a
l
l
C
d
+
F
b
i
g
d
+
X
W
d
×
F
W
(20)
F_d =FsmallA_d+FsmallB_d+FsmallC_d+Fbig_d+XW_d\times FW \tag{20}
Fd=FsmallAd+FsmallBd+FsmallCd+Fbigd+XWd×FW(20)
5.1.10 目标函数
要求总成本最小,即库存费用与生产准备费用之和最小,即可得到目标函数:
m
i
n
C
=
∑
d
=
1
7
R
d
+
∑
d
=
1
7
F
d
(21)
min C=\sum_{d=1}^7R_d+\sum_{d=1}^7 F_d \tag{21}
minC=d=1∑7Rd+d=1∑7Fd(21)

5.2 问题一模型的求解
将模拟退火算法与粒子群算法相结合,使用MATLAB编写代码,求得问题一结果,如下所示。
clear all
clc
#每天WPCR需求量
WPCR=[39363840373340];#一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;#每天总工时
T=[4500250027502100250027501500];#ABC单位工时消耗
TA=3;
TB=5;
TC=5;#生产准备费用:A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[24012040605016080100180604070];#单件库存费用:A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[525361.5451.7323];#模拟退火-粒子群算法
T0=100;#初始化温度值
T_min=1;#设置温度下界
alpha=0.95;#温度的下降率
c1=0.4;c2=0.6;#学习因子
wmax=0.6;wmin=0.4;#惯性权重
num=1000;#颗粒总数,效果不好可以增加
X=[];
F=[];for i=1:num
[X(i,:),F(i,1)]=chushihua1(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C);
end
#以最小化为例[bestf,a]=min(F);
bestx=X(a,:);
trace(1)=bestf;while(T0>T_min)
XX=[];
FF=[];for i=1:num
[XX(i,:),FF(i,1)]=chushihua1(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C);
delta=FF(i,1)-F(i,1);if delta<0
F(i,1)=FF(i,1);
X(i,:)=XX(i,:);else
P=exp(-delta/T0);if P>rand
F(i,1)=FF(i,1);
X(i,:)=XX(i,:);
end
end
end
fave=mean(F);
fmin=min(F);for i=1:num
#权重更新if F(i)<=fave
w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);else
w=wmax;
end
[~,b]=min(F);
best=X(b,:);#当前最优解
v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));#速度
XX(i,:)=round(X(i,:)+v);#更新位置
XX(i,:)=max(XX(i,:),0);#不能小于0#检验,不满足条件则返回之前的变量
x=reshape(XX(i,:)',7,4)';#重新排列矩阵维度
J=jianyan1(X,WPCR,A_x,B_x,C_x);if length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))>0|sum(x(1,:))<sum(WPCR)| J==1
XX(i,:)=X(i,:);
end
#计算目标函数
FF(i,1)=fun1(X(i,:),WPCR,A_x,B_x,C_x,W,C);#更新最优if FF(i,1)<F(i,1)
F(i,1)=FF(i,1);
X(i,:)=XX(i,:);
end
end
ifmin(F)<bestf
[bestf,a]=min(F);
bestx=X(a,:);
end
trace=[trace;bestf];
T0=T0*alpha;
end
disp('最优解为:')
disp('WPCR组装数量、A组装数量、B组装数量、C组装数量')
disp(reshape(bestx',7,4))
disp('生产准备费用、库存费用')[~,f1,f2]=fun1(bestx,WPCR,A_x,B_x,C_x,W,C)
disp('总费用')
disp(bestf)
figure
plot(trace)
xlabel('迭代次数')
ylabel('函数值')
title('模拟退火算法')
legend('最优值')
function [X,F]=chushihua1(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C)#初始化变量、计算目标函数值
flag1=0;while flag1==0
X=[];
flag1=1;
KC_WPCR=zeros(1,length(WPCR));#记录每天WPCR库存
KC=zeros(3,length(WPCR));#记录每天ABC库存
SY_WPCR=zeros(1,length(WPCR));#记录每天交付WPCR情况
SY=zeros(3,length(WPCR));#记录每天使用ABC情况
SC_WPCR=zeros(1,length(WPCR));#记录每天组装WPCR情况
SC=zeros(3,length(WPCR));#记录每天生产ABC情况for i=1:length(WPCR)#循环遍历每个WPCRif i==1#第一天0库存
sub=[A_x,B_x,C_x].*WPCR(i);#求出每天的最小ABC需求量
up=[];
up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);#BC最低供应时,A最大供应量
up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);#AC最低供应时,B最大供应量
up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);#AC最低供应时,B最大供应量
up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])).*[A_x,B_x,C_x]);else
sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i-1)',0);#除了第一天,每天减去前一天的库存则为当天至少增加的需求量
up=[];
up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);#BC最低供应时,A最大供应量
up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);#AC最低供应时,B最大供应量
up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);#AC最低供应时,B最大供应量
up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])).*[A_x,B_x,C_x]);
end
#前面的变量会影响后面的变量范围,可能会出现上up小于sub的情况,毕竟有最大工时限制if length(find((up-sub)<0))>0#如果出现则重新生成
flag1=0;continue
end
flag2=0;while flag2==0
x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];#在区间内随机生成整数if x*[TA;TB;TC]<=T(i)#需求量必须满足在工时限制内
flag2=1;
end
end
#每天组装的WPCRif i==1
s=WPCR(i);#可组装最小数量
u=min(fix(x./[A_x,B_x,C_x]));#可组装最大数量else
s=WPCR(i)-KC_WPCR(i-1);
u=min(fix([x+KC(:,i-1)']./[A_x,B_x,C_x]));
end
#更新SC、KC、SY矩阵#生产
SC_WPCR(i)=randi([s,u]);
SC(:,i)=SC(:,i)+x';#放库存if i==1
KC_WPCR(i)=KC_WPCR(i)+SC_WPCR(i);
KC(:,i)=KC(:,i)+SC(:,i);else
KC_WPCR(i)=KC_WPCR(i-1)+SC_WPCR(i);
KC(:,i)=KC(:,i-1)+SC(:,i);
end
#使用
SY_WPCR(i)=WPCR(i);
SY(:,i)=[A_x;B_x;C_x].*SC_WPCR(i);#更新库存
KC_WPCR(i)=KC_WPCR(i)-WPCR(i);
KC(:,i)=KC(:,i)-SY(:,i);
end
X=[SC_WPCR;SC];
X=reshape(X',1,28);
end
X1=[SC_WPCR;SC];#生产
X2=[KC_WPCR;KC];#库存
X1(find(X1>0))=1;#最优情况,小件无库存但是有生产准备费用
f1=sum(X1.*[W(1);sum(W(2:5));sum(W(6:8));sum(W(9:12))],2);
f2=sum(X2.*C([1,2,6,9])',2);
F=sum(f1)+sum(f2);"
function J=jianyan1(X,WPCR,A_x,B_x,C_x)#检验变量参与运算后是否出现小于0的值,是则不满足条件
X=X';
KC_WPCR=zeros(1,length(WPCR));#记录每天WPCR库存
KC=zeros(3,length(WPCR));#记录每天ABC库存
SY_WPCR=zeros(1,length(WPCR));#记录每天交付WPCR情况
SY=zeros(3,length(WPCR));#记录每天使用ABC情况
SC_WPCR=zeros(1,length(WPCR));#记录每天组装WPCR情况
SC=zeros(3,length(WPCR));#记录每天生产ABC情况for i=1:length(WPCR)#循环遍历每个WPCR
x=X(i,2:4);#更新SC、KC、SY矩阵#生产
SC_WPCR(i)=X(i,1);
SC(:,i)=SC(:,i)+x';#放库存if i==1
KC_WPCR(i)=KC_WPCR(i)+SC_WPCR(i);
KC(:,i)=KC(:,i)+SC(:,i);else
KC_WPCR(i)=KC_WPCR(i-1)+SC_WPCR(i);
KC(:,i)=KC(:,i-1)+SC(:,i);
end
#使用
SY_WPCR(i)=WPCR(i);
SY(:,i)=[A_x;B_x;C_x].*SC_WPCR(i);#更新库存
KC_WPCR(i)=KC_WPCR(i)-WPCR(i);
KC(:,i)=KC(:,i)-SY(:,i);
end
if length(find(KC_WPCR<0))>0| length(find(KC<0))>0
J=1;else
J=0;
end
六、问题二模型的简历与求解
6.1 问题二模型的建立
6.1.1 小组件组装大组件
组件A、B、C需要提前一天生产入库才能组装 WPCR,A1、A2、A3、B1、B2、C1、C2、C3也需要提前一天生产入库才能组装A、B、C。因此,若想在周一有组件完成订单需求,则上周周日需要组装好周一需要的大组件A、B、C。而上周周日,用于组装大组件的小组件,则应当在上周周六组装好。
因此,第d天用于组装大组件的小组件的数量,应当是第d-1天组装完成的小组件数量与第d―1剩余的小组件数量之和。因此对(5) (6)式进行修改,得到大组件的约束条件,如下所示:
M
A
d
⩽
m
i
n
[
(
M
A
1
d
−
1
+
S
A
1
d
−
1
6
,
M
A
2
d
−
1
+
S
A
2
d
−
1
8
,
M
A
3
d
−
1
+
S
A
3
d
−
1
2
)
]
MA_d \leqslant min\left[ \begin{pmatrix} \frac{MA1_{d-1}+SA1_{d-1}}{6}, \frac{MA2_{d-1}+SA2_{d-1}}{8}, \frac{MA3_{d-1}+SA3_{d-1}}{2} \end{pmatrix} \right]
MAd⩽min[(6MA1d−1+SA1d−1,8MA2d−1+SA2d−1,2MA3d−1+SA3d−1)]
M
B
d
⩽
m
i
n
[
(
M
B
1
d
−
1
+
S
B
1
d
−
1
2
,
M
B
2
d
−
1
+
S
B
2
d
−
1
4
,
)
]
(22)
MB_d \leqslant min\left[ \begin{pmatrix} \frac{MB1_{d-1}+SB1_{d-1}}{2}, \frac{MB2_{d-1}+SB2_{d-1}}{4}, \end{pmatrix} \right]\tag{22}
MBd⩽min[(2MB1d−1+SB1d−1,4MB2d−1+SB2d−1,)](22)
M
C
d
⩽
m
i
n
[
(
M
C
1
d
−
1
+
S
C
1
d
−
1
8
,
M
C
2
d
−
1
+
S
C
2
d
−
1
2
,
M
C
3
d
−
1
+
S
C
3
d
−
1
12
)
]
MC_d \leqslant min\left[ \begin{pmatrix} \frac{MC1_{d-1}+SC1_{d-1}}{8}, \frac{MC2_{d-1}+SC2_{d-1}}{2}, \frac{MC3_{d-1}+SC3_{d-1}}{12} \end{pmatrix} \right]
MCd⩽min[(8MC1d−1+SC1d−1,2MC2d−1+SC2d−1,12MC3d−1+SC3d−1)]
6.1.2 小组件的剩余
第d天剩余的小组件数量,即需要存储的小组件数量,可以看为两部分。一部分为第d天组装的小组件数量,另一部分为第d天组装大组件的剩余部分,而剩余部分,应当是d-1天组装完成的小组件与第d―1剩余的小组件数量之和,减去第d天所消耗的数量,
第
d
天剩余
{
第
d
天组装的数量
+
(第
d
−
1
天组装的数量
+
第
d
−
1
天剩余的数量)
−
第
d
天消耗的数量
第d天剩余\begin{cases} 第d天组装的数量\\ +\\ (第d-1天组装的数量+第d-1天剩余的数量)-第d天消耗的数量 \end{cases}
第d天剩余⎩⎨⎧第d天组装的数量+(第d−1天组装的数量+第d−1天剩余的数量)−第d天消耗的数量
因此,小组件的剩余如下所示:
S
A
1
d
=
M
A
1
d
+
M
A
1
d
−
1
+
S
A
1
d
−
1
−
6
×
M
A
d
SA1_d=MA1_d+MA1_{d-1}+SA1_{d-1}-6 \times MA_d
SA1d=MA1d+MA1d−1+SA1d−1−6×MAd
S
A
2
d
=
M
A
2
d
+
M
A
2
d
−
1
+
S
A
2
d
−
1
−
8
×
M
A
d
SA2_d=MA2_d+MA2_{d-1}+SA2_{d-1}-8 \times MA_d
SA2d=MA2d+MA2d−1+SA2d−1−8×MAd
S
A
3
d
=
M
A
3
d
+
M
A
3
d
−
1
+
S
A
3
d
−
1
−
2
×
M
A
d
SA3_d=MA3_d+MA3_{d-1}+SA3_{d-1}-2 \times MA_d
SA3d=MA3d+MA3d−1+SA3d−1−2×MAd
S
B
1
d
=
M
B
1
d
+
M
B
1
d
−
1
+
S
B
1
d
−
1
−
2
×
M
B
d
SB1_d=MB1_d+MB1_{d-1}+SB1_{d-1}-2 \times MB_d
SB1d=MB1d+MB1d−1+SB1d−1−2×MBd
S
B
2
d
=
M
B
2
d
+
M
B
2
d
−
1
+
S
B
2
d
−
1
−
4
×
M
B
d
(23)
SB2_d=MB2_d+MB2_{d-1}+SB2_{d-1}-4 \times MB_d \tag{23}
SB2d=MB2d+MB2d−1+SB2d−1−4×MBd(23)
S
C
1
d
=
M
C
1
d
+
M
C
1
d
−
1
+
S
C
1
d
−
1
−
8
×
M
C
d
SC1_d=MC1_d+MC1_{d-1}+SC1_{d-1}-8 \times MC_d
SC1d=MC1d+MC1d−1+SC1d−1−8×MCd
S
C
2
d
=
M
C
2
d
+
M
C
2
d
−
1
+
S
C
2
d
−
1
−
2
×
M
C
d
SC2_d=MC2_d+MC2_{d-1}+SC2_{d-1}-2 \times MC_d
SC2d=MC2d+MC2d−1+SC2d−1−2×MCd
S
C
3
d
=
M
C
3
d
+
M
C
3
d
−
1
+
S
C
3
d
−
1
−
12
×
M
C
d
SC3_d=MC3_d+MC3_{d-1}+SC3_{d-1}-12 \times MC_d
SC3d=MC3d+MC3d−1+SC3d−1−12×MCd
6.1.3 机器人的组装数量计算 大组件剩余
机器人的组装与小组件组装大组件同理,第d天使用第d-1天组装或剩余的大组件组装机器人,约束条件如下所示:
M
W
d
⩽
m
i
n
[
(
M
A
1
d
−
1
+
S
A
1
d
−
1
3
,
M
B
2
d
−
1
+
S
B
2
d
−
1
4
,
M
C
3
d
−
1
+
S
C
3
d
−
1
5
)
]
(24)
MW_d \leqslant min\left[ \begin{pmatrix} \frac{MA1_{d-1}+SA1_{d-1}}{3}, \frac{MB2_{d-1}+SB2_{d-1}}{4}, \frac{MC3_{d-1}+SC3_{d-1}}{5} \end{pmatrix} \right]\tag{24}
MWd⩽min[(3MA1d−1+SA1d−1,4MB2d−1+SB2d−1,5MC3d−1+SC3d−1)](24)
大组件的剩余与小组件的剩余同理,如下所示:
S
A
d
=
M
A
d
+
M
A
d
−
1
+
S
A
d
−
1
−
3
×
M
W
d
SA_d=MA_d+MA_{d-1}+SA_{d-1}-3 \times MW_d
SAd=MAd+MAd−1+SAd−1−3×MWd
S
B
d
=
M
B
d
+
M
B
d
−
1
+
S
B
d
−
1
−
4
×
M
W
d
(25)
SB_d=MB_d+MB_{d-1}+SB_{d-1}-4 \times MW_d \tag{25}
SBd=MBd+MBd−1+SBd−1−4×MWd(25)
S
C
d
=
M
C
d
+
M
C
d
−
1
+
S
C
d
−
1
−
5
×
M
W
d
SC_d=MC_d+MC_{d-1}+SC_{d-1}-5 \times MW_d
SCd=MCd+MCd−1+SCd−1−5×MWd
6.1.4 机器人的组装数量约束与剩余计算
机器人的组装数量与剩余未修改,如下所示:
M
W
d
+
S
W
d
−
1
⩾
D
W
d
(26)
MW_d+SW_{d-1} \geqslant DW_d \tag{26}
MWd+SWd−1⩾DWd(26)
S
W
d
=
M
C
d
+
M
W
d
−
1
+
S
W
d
−
1
−
D
W
d
(26)
SW_d=MC_d+MW_{d-1}+SW_{d-1}-DW_d \tag{26}
SWd=MCd+MWd−1+SWd−1−DWd(26)
6.1.5 保障第二天的生产
为了保障下周周一的生产,本周周日结束便应当留下组件,因此问题一中的(13)(14)式应当不考虑。将下周周一看作第8天,因此第8天组装机器人的数量与第7天机器人的剩余数量之和应当不小于下周周一的订单数量39,如下所示:
M
W
8
+
S
W
8
−
1
⩾
39
(26)
MW_8+SW_{8-1} \geqslant 39 \tag{26}
MW8+SW8−1⩾39(26)
值得注意的是,在本周中,并未明确给出为了保障第d天机器人的生产,而对第d天的大组件的组装数量、第d-1天小组件组装数量的约束条件。但在(26)式中,有第d天机器人订单数量DWd,对第d天制造数量MWd的约束,在(24)式中有第d天机器人制造数量MWd,对第d-1天大组件的组装数量的约束,在(22)式中有第d天大组件组装数量对第d-1天小组件的组装数量的约束。
因此,保障第二天机器人生产数量的约束条件虽未明确给出,但己被暗含其中。
6.1.6 工时的限制
工时的限制并未修改,如下所示:
3
×
M
A
d
+
5
×
M
B
d
+
5
×
M
C
d
⩽
T
d
(27)
3\times MA_d+5\times MB_d+5\times MC_d \leqslant T_d \tag{27}
3×MAd+5×MBd+5×MCd⩽Td(27)
6.1.7 目标函数
目标函数并未修改,与问题一相同,如下所示:
m
i
n
C
=
∑
d
=
1
7
R
d
+
∑
d
=
1
7
F
d
(28)
min C=\sum_{d=1}^7R_d+\sum_{d=1}^7 F_d \tag{28}
minC=d=1∑7Rd+d=1∑7Fd(28)

6.2 问题二模型的求解
使用MATLAB编写代码,求得问题二的结果。
clear
clc
#每天WPCR需求量
WPCR=[39363840373340];#一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;
D_x=[6;8;2;2;4;8;2;12];#每天总工时
T=[4500250027502100250027501500];#ABC单位工时消耗
TA=3;
TB=5;
TC=5;#生产准备费用:A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[24012040605016080100180604070];#单件库存费用:A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[525361.5451.7323];#模拟退火-粒子群算法
T0=100;#初始化温度值
T_min=1;#设置温度下界
alpha=0.95;#温度的下降率
c1=0.4;c2=0.6;#学习因子
wmax=0.6;wmin=0.4;#惯性权重
num=1000;#颗粒总数
X=[];
F=[];for i=1:num
[X(i,:),F(i,1)]=chushihua2(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
end
#以最小化为例[bestf,a]=min(F);
bestx=X(a,:);
trace(1)=bestf;while(T0>T_min)
XX=[];
FF=[];for i=1:num
[XX(i,:),FF(i,1)]=chushihua2(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
delta=FF(i,1)-F(i,1);if delta<0
F(i,1)=FF(i,1);
X(i,:)=XX(i,:);else
P=exp(-delta/T0);if P>rand
F(i,1)=FF(i,1);
X(i,:)=XX(i,:);
end
end
end
fave=mean(F);
fmin=min(F);for i=1:num
#权重更新if F(i)<=fave
w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);else
w=wmax;
end
[~,b]=min(F);
best=X(b,:);#当前最优解
v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));%速度
XX(i,:)=round(X(i,:)+v);#更新位置
XX(i,:)=max(XX(i,:),0);#不能小于0#检验,不满足条件则返回之前的变量
x=reshape(XX(i,:)',7,4)';#重新排列矩阵维度
J=jianyan2(X,WPCR,A_x,B_x,C_x,D_x);if length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))>0|sum(x(1,:))<sum(WPCR)| J==1
XX(i,:)=X(i,:);
end
#计算目标函数
FF(i,1)=fun2(X(i,:),WPCR,A_x,B_x,C_x,W,C,D_x);#更新最优if FF(i,1)<F(i,1)
F(i,1)=FF(i,1);
X(i,:)=XX(i,:);
end
end
ifmin(F)<bestf
[bestf,a]=min(F);
bestx=X(a,:);
end
trace=[trace;bestf];
T0=T0*alpha;
end
disp('最优解为:')
disp('WPCR组装数量、A组装数量、B组装数量、C组装数量')
disp(reshape(bestx',7,4))
disp('生产准备费用、库存费用')[~,f1,f2]=fun2(bestx,WPCR,A_x,B_x,C_x,W,C,D_x)
disp('总费用')
disp(bestf)
figure
plot(trace)
xlabel('迭代次数')
ylabel('函数值')
title('模拟退火算法')
legend('最优值')
function [X,F]=chushihua2(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x)#初始化变量、计算目标函数值,小件提前两天,大件提前1天
flag1=0;while flag1==0
X=[];
nn=2;#延迟天数
flag1=1;
KC_WPCR=zeros(1,length(WPCR)+nn);#记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);#记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);#记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);#记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);#记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);#记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);#记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);#记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);#记录每天生产ABC小件情况for i=1:length(WPCR)#循环遍历每个WPCRif i==1#假设第一天刚好满足WPCR
sub=[A_x,B_x,C_x].*WPCR(i);#求出每天的WPCR最小ABC需求量
up=sub;else
sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i+nn-1)',0);#除了第一天,每天减去前一天的库存则为当天至少增加的需求量
up=[];
up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);#BC最低供应时,A最大供应量
up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);#AC最低供应时,B最大供应量
up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);#AC最低供应时,B最大供应量
up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])).*[A_x,B_x,C_x]);
end
#前面的变量会影响后面的变量范围,可能会出现上up小于sub的情况,毕竟有最大工时限制if length(find((up-sub)<0))>0#如果出现则重新生成
flag1=0;continue
end
flag2=0;while flag2==0
x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];#在区间内随机生成整数if x*[TA;TB;TC]<=T(i)#需求量必须满足在工时限制内
flag2=1;
end
end
#每天组装的WPCRif i==1
s=WPCR(i);#可组装最小数量
u=min(fix(x./[A_x,B_x,C_x]));#可组装最大数量else
s=WPCR(i)-KC_WPCR(i+nn-1);
u=min(fix([x+KC(:,i+nn-1)']./[A_x,B_x,C_x]));
end
#更新SC、KC、SY矩阵#生产
SC_WPCR(i+nn)=randi([s,u]);
SC(:,i+nn-1)=SC(:,i+nn-1)+x';
SC_x(1:3,i)=D_x(1:3).*SC(1,i+nn-1);
SC_x(4:5,i)=D_x(4:5).*SC(2,i+nn-1);
SC_x(6:8,i)=D_x(6:8).*SC(3,i+nn-1);#放库存
KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
KC(:,i+nn-1)=KC(:,i+nn-2)+SC(:,i+nn-1);if i==1
KC_x(:,i+nn-2)=SC_x(:,i+nn-2);else
KC_x(:,i+nn-2)=KC_x(:,i+nn-3)+SC_x(:,i+nn-2);
end
#使用
SY_WPCR(i+nn)=WPCR(i);
SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
SY_x(1:3,i+nn-1)=D_x(1:3).*SY(1,i+nn);
SY_x(4:5,i+nn-1)=D_x(4:5).*SY(2,i+nn);
SY_x(6:8,i+nn-1)=D_x(6:8).*SY(3,i+nn);#更新库存
KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
KC_x(:,i+nn-1)=KC_x(:,i+nn-2)-SY_x(:,i+nn-1);
end
X=[SC_WPCR(:,nn+1:end);SC(:,nn:end-1)];
X=reshape(X',1,28);
end
X1=[SC_WPCR(:,nn+1:end);SC(:,nn+1:end)];#生产
X2=[SC_x(:,nn+1:end)];#生产ABC小件
X3=[KC_WPCR(:,nn+1:end);KC(:,nn+1:end)];#库存ABC
X4=[KC_x(:,nn+1:end)];#库存ABC小件
X1(find(X1>0))=1;
X2(find(X2>0))=1;#最优情况,小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);
function [F,f1,f2]=fun2(X,WPCR,A_x,B_x,C_x,W,C,D_x)#初始化变量、计算目标函数值
X=reshape(X',7,4);
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);#记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);#记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);#记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);#记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);#记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);#记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);#记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);#记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);#记录每天生产ABC小件情况for i=1:length(WPCR)#循环遍历每个WPCR
x=X(i,2:4);#更新SC、KC、SY矩阵#生产
SC_WPCR(i+nn)=X(i,1);
SC(:,i+nn-1)=SC(:,i+nn-1)+x';
SC_x(1:3,i)=D_x(1:3).*SC(1,i+nn-1);
SC_x(4:5,i)=D_x(4:5).*SC(2,i+nn-1);
SC_x(6:8,i)=D_x(6:8).*SC(3,i+nn-1);#放库存
KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
KC(:,i+nn-1)=KC(:,i+nn-2)+SC(:,i+nn-1);if i==1
KC_x(:,i+nn-2)=SC_x(:,i+nn-2);else
KC_x(:,i+nn-2)=KC_x(:,i+nn-3)+SC_x(:,i+nn-2);
end
#使用
SY_WPCR(i+nn)=WPCR(i);
SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
SY_x(1:3,i+nn-1)=D_x(1:3).*SY(1,i+nn);
SY_x(4:5,i+nn-1)=D_x(4:5).*SY(2,i+nn);
SY_x(6:8,i+nn-1)=D_x(6:8).*SY(3,i+nn);#更新库存
KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
KC_x(:,i+nn-1)=KC_x(:,i+nn-2)-SY_x(:,i+nn-1);
end
X1=[SC_WPCR(:,nn+1:end);SC(:,nn+1:end)];#生产
X2=[SC_x(:,nn+1:end)];#生产ABC小件
X3=[KC_WPCR(:,nn+1:end);KC(:,nn+1:end)];#库存ABC
X4=[KC_x(:,nn+1:end)];#库存ABC小件
X1(find(X1>0))=1;
X2(find(X2>0))=1;#最优情况,小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);
function J=jianyan2(X,WPCR,A_x,B_x,C_x,D_x)#检验变量参与运算后是否出现小于0的值,是则不满足条件
X=X';
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);#记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);#记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);#记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);#记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);#记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);#记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);#记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);#记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);#记录每天生产ABC小件情况for i=1:length(WPCR)#循环遍历每个WPCR
x=X(i,2:4);#更新SC、KC、SY矩阵#生产
SC_WPCR(i+nn)=X(i,1);
SC(:,i+nn-1)=SC(:,i+nn-1)+x';
SC_x(1:3,i)=D_x(1:3).*SC(1,i+nn-1);
SC_x(4:5,i)=D_x(4:5).*SC(2,i+nn-1);
SC_x(6:8,i)=D_x(6:8).*SC(3,i+nn-1);#放库存
KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);
KC(:,i+nn-1)=KC(:,i+nn-2)+SC(:,i+nn-1);if i==1
KC_x(:,i+nn-2)=SC_x(:,i+nn-2);else
KC_x(:,i+nn-2)=KC_x(:,i+nn-3)+SC_x(:,i+nn-2);
end
#使用
SY_WPCR(i+nn)=WPCR(i);
SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);
SY_x(1:3,i+nn-1)=D_x(1:3).*SY(1,i+nn);
SY_x(4:5,i+nn-1)=D_x(4:5).*SY(2,i+nn);
SY_x(6:8,i+nn-1)=D_x(6:8).*SY(3,i+nn);#更新库存
KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
KC_x(:,i+nn-1)=KC_x(:,i+nn-2)-SY_x(:,i+nn-1);
end
if length(find(KC_WPCR<0))>0| length(find(KC<0))>0| length(find(KC_x<0))>0
J=1;else
J=0;
end
七、问题三模型的建立与求解
7.1 问题三模型的建立
7.1.1 时间变量的确定
本问中,时间由7天变为了30周210天,因此时间变量为
d
∈
(
−
1
,
0
,
1
,
.
.
.
,
208
,
209
,
210
)
(29)
d∈(-1,0,1,...,208,209,210)\tag{29}
d∈(−1,0,1,...,208,209,210)(29)
d=-1即第1周的上一周的周六,d=0为第1周的上一周的周日。d=1为第1周的周一,即该30周的第1天;d=210为第30周的周日,即该30周的最后一天。
7.1.2 停工检修的0-1变量
在建模中,若遇到变量可以取多个整数值的问题时,利用0-1变量是二进制变量的性质,可以使用一组0-1变量来取代该变量。因此,借助该性质,引入一组0-1变量来取代一个停工检修的0-1变量。
以第1次检修日期为例,建立关于第一次检修日的模型如下:
c
h
e
c
k
i
=
{
1
第
i
天要检修
0
第
i
天不检修
(29)
check_i=\begin{cases} 1 & 第i天要检修 \\ 0 & 第i天不检修 \\ \end{cases}\tag{29}
checki={10第i天要检修第i天不检修(29)

上式中,第一个式子为0-1变量,含义为第1次的检修日期是否为第d天。因为第1次检修日只能在这210天中的某一天,即只能是1天,所以引入上式第二个式子用于约束。
为了能够方便地得到第1次检修的日期的具体数值,故借助0-1变量是二进制变量(binary variable)的性质,引入上式中的第三个式子。例如第1次检修的日期为第3天,则
θ
13
=
1
(31)
θ_{13}=1 \tag{31}
θ13=1(31)
θ
11
=
θ
12
=
θ
14
=
.
.
.
=
θ
11
=
θ
1
(
210
)
=
0
(31)
θ_{11}=θ_{12}=θ_{14}=...=θ_{11}=θ_{1(210)}=0 \tag{31}
θ11=θ12=θ14=...=θ11=θ1(210)=0(31)
此时已经满足(30)式第二个式子。
则(30)式的第三个式子可以转化为:
c
h
e
c
k
1
=
2
1
θ
11
+
2
2
θ
12
+
.
.
.
+
2
210
θ
(
1
)
210
=
2
1
×
0
+
2
2
×
0
+
2
3
×
1
+
.
.
.
+
2
210
×
0
=
2
3
(31)
check_{1}=2^1θ_{11}+2^2θ_{12}+...+2^{210}θ_{(1)210} =2^1 \times 0+2^2 \times 0+2^3 \times 1+...+2^{210} \times 0=2^3 \tag{31}
check1=21θ11+22θ12+...+2210θ(1)210=21×0+22×0+23×1+...+2210×0=23(31)
通过(30)式第四个式子,可以直接得到第1次检修的日期,如下所示:
c
h
e
c
k
D
a
t
e
1
=
l
o
g
2
c
h
e
c
k
1
=
l
o
g
2
(
2
3
)
=
3
(32)
checkDate_1=log_2^{check1}=log_2^{(2^3)}=3 \tag{32}
checkDate1=log2check1=log2(23)=3(32)
因此,便得到了7次检修的0-1变量,如下所示:
其中,chechDatet 为第t次检修的具体日期。
7.1.3 检修间隔
为更加便利地给出两两检修日期间隔6天,先限制7次检修的顺序,即先对checkDatet,排序,如下所示:
c
h
e
c
h
D
a
t
e
i
<
c
h
e
c
h
D
a
t
e
i
+
1
,
i
∈
(
1
,
2
,
3...5
,
6
)
(34)
chechDate~i~ < chechDate~i+1~ ,i∈(1,2,3...5,6)\tag{34}
chechDate i <chechDate i+1 ,i∈(1,2,3...5,6)(34)
排序后,便给出两两检修日期间隔6天的约束,如下所示:
c
h
e
c
h
D
a
t
e
i
+
6
<
c
h
e
c
h
D
a
t
e
i
+
1
,
i
∈
(
1
,
2
,
3...5
,
6
)
(35)
chechDate~i~ +6< chechDate~i+1~ ,i∈(1,2,3...5,6)\tag{35}
chechDate i +6<chechDate i+1 ,i∈(1,2,3...5,6)(35)
7.1.4 定义大总工时限制矩阵
本问中的生产时长由7天变为了30周的210天,故重新定义大总工时限制矩阵: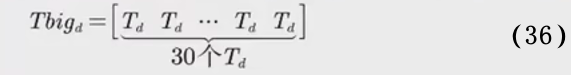
其中,Td 一周中第d天总工时限制。
故满足总工时限制的约束如下:
3
×
M
A
d
+
5
×
M
B
d
+
5
×
M
C
d
⩽
T
b
i
g
d
(37)
3 \times MA~d~ +5\times MB~d~ +5\times MC_d\leqslant Tbig_d \tag{37}
3×MA d +5×MB d +5×MCd⩽Tbigd(37)
7.1.5 检修后总工时限制放宽
对设备检修之后,生产能力有所提高,检修后的第1天后,生产总工时限制依次放宽10%、8%、…、2%、0%。因此在确定了7次检修的具体日期后,便可更改大总工时限制矩阵中的数值,使其满足检修后的放宽。更改公式如下所示:
T
b
i
g
(
c
h
e
c
h
D
a
t
e
+
o
f
f
s
e
t
)
=
T
b
i
g
(
c
h
e
c
h
D
a
t
e
+
o
f
f
s
e
t
)
×
(
1
+
(
0.1
−
0.02
×
o
f
f
s
e
t
)
)
(38)
Tbig_{(chechDate+offset)}= Tbig_{(chechDate+offset)} \times (1+(0.1-0.02 \times offset)) \tag{38}
Tbig(chechDate+offset)=Tbig(chechDate+offset)×(1+(0.1−0.02×offset))(38)
o
f
f
s
e
t
∈
(
0
,
1
,
.
.
.
4
,
5
)
offset∈(0,1,...4,5)
offset∈(0,1,...4,5)
其中1,offset为日期偏移量,从每次检修的日期向后偏移,每偏移一次,限制放宽减少2%。在偏移到5次时,限制放宽减少到0%,停止偏移。
7.1.6 检修日不能生产任何组件
设备检修日,不能生产任何组件,即检修日大组件,小组件,机器人的产量都为0,故约束条件如下:
M
A
1
j
=
M
A
2
j
=
M
A
3
j
=
M
B
1
j
=
M
B
2
j
=
M
C
1
j
=
M
C
2
j
=
M
C
3
j
=
0
MA1_j=MA2_j=MA3_j=MB1_j=MB2_j=MC1_j=MC2_j=MC3_j=0
MA1j=MA2j=MA3j=MB1j=MB2j=MC1j=MC2j=MC3j=0
M
A
j
=
M
B
j
=
M
C
j
=
M
W
j
=
0
(39)
MA_j=MB_j=MC_j=MW_j=0 \tag{39}
MAj=MBj=MCj=MWj=0(39)
j
∈
(
c
h
e
c
k
D
a
t
e
t
,
t
∈
(
1
,
2
,
.
.
.
6
,
7
)
)
j∈(checkDate_t,t∈(1,2,...6,7))
j∈(checkDatet,t∈(1,2,...6,7))
7.1.7 保证生产可以继续
为了保证30周210天结束后,第31周的周一,即第211天仍能够完成订单需求,故第211天机器人的生产数量 MW与第210天机器人的剩余数量SW11-,应不小于第211天机器人的需求量DW.1,其原理与6.1.5相同。约束条件如下所示:
M
W
211
+
S
W
211
−
1
⩾
D
W
211
(40)
MW_{211}+SW_{211-1}\geqslant DW_{211} \tag{40}
MW211+SW211−1⩾DW211(40)
题目中并未给出第211天机器人的需求量DW_{211},此处对30周的周一数据求平均并四舍五入,得到DW211=38。
其他约束条件与目标函数并未在问题二的模型进行改动,故此处不再赘述。
7.2 问题三模型的求解
使用MATLAB编写代码,求得问题三的结果。
clear
clc
#每天WPCR需求量
WPCR=[393638403733403933374334303942363538363541383636483435393836404040343940303640343637413641413829433331404242304035363833353741433542373633393832413640313437374139383538383833424229333937443835363840393838373444353638393939394328394138303835374041403541363540413738363738394138374437373736393341393742373628434032354540344338363736402845384038363540423131443631364040363443353239333336413438403534373739364037413941363244];
WPCR=reshape(WPCR',210,1)';
WPCR=[WPCR,WPCR(1:2)];#一个WPCR队ABC需求比例
A_x=3;
B_x=4;
C_x=5;
D_x=[6;8;2;2;4;8;2;12];#每天总工时
T=repmat([4500250027502100250027501500],1,30);
T=[T(end),T,T(1)];#ABC单位工时消耗
TA=3;
TB=5;
TC=5;#生产准备费用:A A1 A2 A3 B B1 B2 C C1 C2 C3
W=[24012040605016080100180604070];#单件库存费用:A A1 A2 A3 B B1 B2 C C1 C2 C3
C=[525361.5451.7323];#模拟退火-粒子群算法
T0=100;#初始化温度值
T_min=1;#设置温度下界
alpha=0.9;#温度的下降率
c1=0.4;c2=0.6;#学习因子
wmax=0.6;wmin=0.4;#惯性权重
num=2;#颗粒总数
X=[];
A=[];
F=[];for i=1:num
[X(i,:),A(i,:),F(i,1)]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
end
#以最小化为例[bestf,a]=min(F);
bestx=X(a,:);
bestA=A(a,:);
trace(1)=bestf;while(T0>T_min)
XX=[];
FF=[];
AA=[];for i=1:num
[XX(i,:),AA(i,:),FF(i,1)]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x);
delta=FF(i,1)-F(i,1);if delta<0
F(i,1)=FF(i,1);
X(i,:)=XX(i,:);
A(i,:)=AA(i,:);else
P=exp(-delta/T0);if P>rand
F(i,1)=FF(i,1);
X(i,:)=XX(i,:);
A(i,:)=AA(i,:);
end
end
end
fave=mean(F);
fmin=min(F);for i=1:num
#权重更新if F(i)<=fave
w=wmin+(F(i)-fmin)*(wmax-wmin)/(fave-fmin);else
w=wmax;
end
[~,b]=min(F);
best=X(b,:);#当前最优解#粒子群算法限制最多找10次位置
m=1;
flag=0;while flag==1
v=w.*randn(1,28)+c1*rand*(best-X(i,:))+c2*rand*(bestx-X(i,:));#速度
XX(i,:)=round(X(i,:)+v);#更新位置
XX(i,:)=max(XX(i,:),0);#不能小于0#检验,不满足条件则返回之前的变量
x=reshape(XX(i,:)',7,4)';#重新排列矩阵维度
J=jianyan3(x,AA(i,:),WPCR,A_x,B_x,C_x);if(length(find((sum(x(2:4,:).*[TA;TB;TC],1)-T)>0))==0&sum(x(1,:))>=sum(WPCR)& J==0)| m==10
XX(i,:)=X(i,:);else
m=m+1;
end
end
#计算目标函数
FF(i,1)=fun3(XX(i,:),AA(i,:),WPCR,A_x,B_x,C_x,W,C,D_x);#更新最优if FF(i,1)<F(i,1)
F(i,1)=FF(i,1);
X(i,:)=XX(i,:);
A(i,:)=AA(i,:);
end
end
ifmin(F)<bestf
[bestf,a]=min(F);
bestx=X(a,:);
bestA=A(a,:);
end
trace=[trace;bestf];
T0=T0*alpha;
end
disp('最优解为:')
disp('停检时间')
disp(bestA)
disp('WPCR组装数量、A组装数量、B组装数量、C组装数量,见工作区矩阵zz')
x=reshape(bestx',212,4);
zz=[x(1:210,1),x(2:211,2:4)];
disp('生产准备费用、库存费用见工作区矩阵f1、f2')[~,f1,f2]=fun3(bestx,bestA,WPCR,A_x,B_x,C_x,W,C,D_x);
disp('总费用')
disp(bestf)
figure
plot(trace)
xlabel('迭代次数')
ylabel('函数值')
title('模拟退火算法')
legend('最优值')
function [X,b,F]=chushihua3(WPCR,A_x,B_x,C_x,T,TA,TB,TC,W,C,D_x)#初始化变量、计算目标函数值,小件提前两天,大件提前1天
flag1=0;while flag1==0#检修
flag3=0;while flag3==0
A=zeros(1,length(WPCR));
a=10+randperm(length(WPCR)-20);
aa=a(1:7);
A(aa)=1;
b=find(A==1);
c=b(2:end)-b(1:end-1);
d=find(c<6);if length(d)==0
flag3=1;
end
end
#检修后提高效率
AA=[];#对应的时间for i=1:length(b)
AA=[AA,b(i)+1:b(i)+5];
end
G=repmat([1.11.081.0610.41.02],1,length(b));
TT=T;
TT(AA)=TT(AA).*G;
X=[];
nn=2;#延迟天数
flag1=1;
KC_WPCR=zeros(1,length(WPCR)+nn);#记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);#记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);#记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);#记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);#记录每天使用ABC情况% SY_x=zeros(8,length(WPCR)+nn);#记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);#记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);#记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);#记录每天生产ABC小件情况for i=1:length(WPCR)#循环遍历每个WPCRif i==1#假设第一天刚好满足WPCR
sub=[A_x,B_x,C_x].*WPCR(i);#求出每天的WPCR最小ABC需求量
up=sub;else
sub=max([A_x,B_x,C_x].*WPCR(i)-KC(:,i+nn-1)',0);#除了第一天,每天减去前一天的库存则为当天至少增加的需求量
up=[];
up(1)=fix((T(i)-sub([2,3])*[TB;TC])/TA);#BC最低供应时,A最大供应量
up(2)=fix((T(i)-sub([1,3])*[TA;TC])/TB);#AC最低供应时,B最大供应量
up(3)=fix((T(i)-sub([1,2])*[TA;TB])/TC);#AC最低供应时,B最大供应量
up=min(up,fix(T(i)./([A_x,B_x,C_x]*[TA;TB;TC])*2).*[A_x,B_x,C_x]);
end
#前面的变量会影响后面的变量范围,可能会出现上up小于sub的情况,毕竟有最大工时限制if length(find((up-sub)<0))>0#如果出现则重新生成
flag1=0;continue
end
flag2=0;while flag2==0
x=[randi([sub(1),up(1)]),randi([sub(2),up(2)]),randi([sub(3),up(3)])];#在区间内随机生成整数if i==1
flag2=1;
elseif i>1if x*[TA;TB;TC]<=T(i)#需求量必须满足在工时限制内
flag2=1;
end
end
end
#每天组装的WPCRif i==1
s=WPCR(i);#可组装最小数量
u=min(fix(x./[A_x,B_x,C_x]));#可组装最大数量else
s=max(WPCR(i)-KC_WPCR(i+nn-1),0);
u=min(fix([x+KC(:,i+nn-1)']./[A_x,B_x,C_x]));
end
if u<s
flag1=0;continue
end
#更新SC、KC、SY矩阵#生产if length(find(b==i))==1
SC_WPCR(i+nn)=0;else
SC_WPCR(i+nn)=randi([s,u]);
end
if length(find(b==i-1))==1
SC(:,i+nn-1)=0;else
SC(:,i+nn-1)=SC(:,i+nn-1)+x';
end
#放库存
KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);if KC_WPCR(i+nn)<0
KC_WPCR(i+nn)=0;
end
if i==1
KC(:,i+nn-1)=SC(:,i+nn-1);else
KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
end
KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);#使用
SY_WPCR(i+nn)=WPCR(i);
SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);#更新库存
KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
X=[SC_WPCR(:,nn+1:end);SC(:,nn:end-1)];
X=reshape(X',1,848);
end
X1=[SC_WPCR(:,nn+1:end-2);SC(:,nn+1:end-2)];#生产
X3=[KC_WPCR(:,nn+1:end-2);KC(:,nn+1:end-2)];#库存ABC
X4=[KC_x(:,nn+1:end-2)];#库存ABC小件
X1(find(X1>0))=1;
X2=[repmat(X1(2,:),3,1);repmat(X1(3,:),2,1);repmat(X1(4,:),3,1)];
X2(:,b)=0;#最优情况,小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);
function [F,f1,f2]=fun3(X,b,WPCR,A_x,B_x,C_x,W,C,D_x)#初始化变量、计算目标函数值
X=reshape(X',212,4);
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);#记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);#记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);#记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);#记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);#记录每天使用ABC情况% SY_x=zeros(8,length(WPCR)+nn);#记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);#记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);#记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);#记录每天生产ABC小件情况for i=1:length(WPCR)#循环遍历每个WPCR
x=X(i,2:4);#更新SC、KC、SY矩阵#生产if length(find(b==i))==1
SC_WPCR(i+nn)=0;else
SC_WPCR(i+nn)=X(i,1);
end
if length(find(b==i-1))==1
SC(:,i+nn-1)=0;else
SC(:,i+nn-1)=SC(:,i+nn-1)+x';
end
#放库存
KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);if KC_WPCR(i+nn)<0
KC_WPCR(i+nn)=0;
end
if i==1
KC(:,i+nn-1)=SC(:,i+nn-1);else
KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
end
KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);#使用
SY_WPCR(i+nn)=WPCR(i);
SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);#更新库存
KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
X1=[SC_WPCR(:,nn+1:end-2);SC(:,nn+1:end-2)];#生产
X3=[KC_WPCR(:,nn+1:end-2);KC(:,nn+1:end-2)];#库存ABC
X4=[KC_x(:,nn+1:end-2)];#库存ABC小件
X1(find(X1>0))=1;
X2=[repmat(X1(2,:),3,1);repmat(X1(3,:),2,1);repmat(X1(4,:),3,1)];
X2(:,b)=0;#最优情况,小件无库存但是有生产准备费用
f1=(sum(X1.*[W(1);W(2);W(6);W(9)],1)+sum(X2.*[W(3:5)';W(7:8)';W(10:12)'],1))';
f2=(sum(X3.*C([1,2,6,9])',1)+sum(X4.*C([3,4,5,7,8,10,11,12])',1))';
F=sum(f1)+sum(f2);
function J=jianyan3(X,b,WPCR,A_x,B_x,C_x,D_x)%检验变量参与运算后是否出现小于0的值,是则不满足条件
X=X';
nn=2;
KC_WPCR=zeros(1,length(WPCR)+nn);#记录每天WPCR库存
KC=zeros(3,length(WPCR)+nn);#记录每天ABC库存
KC_x=zeros(8,length(WPCR)+nn);#记录每天ABC小件库存
SY_WPCR=zeros(1,length(WPCR)+nn);#记录每天交付WPCR情况
SY=zeros(3,length(WPCR)+nn);#记录每天使用ABC情况
SY_x=zeros(8,length(WPCR)+nn);#记录每天使用ABC小件情况
SC_WPCR=zeros(1,length(WPCR)+nn);#记录每天组装WPCR情况
SC=zeros(3,length(WPCR)+nn);#记录每天生产ABC情况
SC_x=zeros(8,length(WPCR)+nn);#记录每天生产ABC小件情况for i=1:length(WPCR)#循环遍历每个WPCR
x=X(i,2:4);#更新SC、KC、SY矩阵#生产if length(find(b==i))==1
SC_WPCR(i+nn)=0;else
SC_WPCR(i+nn)=X(i,1);
end
if length(find(b==i-1))==1
SC(:,i+nn-1)=0;else
SC(:,i+nn-1)=SC(:,i+nn-1)+x';
end
#放库存
KC_WPCR(i+nn)=KC_WPCR(i+nn-1)+SC_WPCR(i+nn);if KC_WPCR(i+nn)<0
KC_WPCR(i+nn)=0;
end
if i==1
KC(:,i+nn-1)=SC(:,i+nn-1);else
KC(:,i+nn-1)=KC(:,i+nn-1)+SC(:,i+nn-1);
end
KC_x(1:3,i+nn-2)=D_x(1:3).*SC(1,i+nn-1);
KC_x(4:5,i+nn-2)=D_x(4:5).*SC(2,i+nn-1);
KC_x(6:8,i+nn-2)=D_x(6:8).*SC(3,i+nn-1);#使用
SY_WPCR(i+nn)=WPCR(i);
SY(:,i+nn)=[A_x;B_x;C_x].*SY_WPCR(i+nn);#更新库存
KC_WPCR(i+nn)=KC_WPCR(i+nn)-WPCR(i);
KC(:,i+nn)=KC(:,i+nn-1)-SY(:,i+nn);
end
if length(find(KC_WPCR<0))>0| length(find(KC<0))>0| length(find(KC_x<0))>0
J=1;else
J=0;
end
八、问题四模型的建立与求解
8.1 问题四模型的建立
8.1.1 数据分析
本问需要预测第31周的机器人的使用需求,由题目给出的数据分析,数据的波动存在一定的周期性,且为时期时间序列数据,只有一个因变量:机器人使用数量。则以机器人使用数量作为因变量,建立基于一元时间序列分析的机器人需求预测模型。
由于以周为时间变量的数据未给出具体周期,考虑将数据分为训练组和实验组,使用不同的周期长度对训练组进行建模,筛选出通过Q检验的模型,再利用实验组的数据判断哪种模型的预测效果最好。选出得到的预测误差最小的那个模型,利用全部数据来重新建模,并对未来的数据进行预测。最后画出预测后的时序图,判断预测趋势是否合理。
8.1.2 数据预处理
观察30周201天的数据,无缺失数据。定义以周为单位的时间变量,以时间为横轴,机器人数量为纵轴绘制时间序列图。分析时间序列图,发现数据在一定范围内上下波动,无趋势、季节性。
8.1.3基于一元时间序列预测模型的建立
训练组数据是为以7为周期长度的序列,利用SPSS专家建模器建立最优时间序列分析模型。专家建模器会自动查找每个相依序列的最佳拟合模型。如果指定了自变量(预测)变量,则专家建模器为ARIMA模型中的内容选择那些与该相依序列具有统计显著关系的模型。适当时,使用差分或平方根或自然对数转换对模型变量进行转换。缺省情况下,专家建模器既考虑指数平滑法模型也考虑ARIMA模型。但是,也可以将专家建模器限制为仅搜索ARIMA模型或仅搜索指数平滑法模型。还可以指定自动检测离群值。
sPSS专家建模器自动为我们选择了最优模型:简单季节性模型。
8.1.4预测模型的检验
检验模型是否识别完全:估计完成时间序列模型后,我们需要对残差进行白噪声检验,如果残差是白噪声,则说明我们选取的模型能完全识别出时间序列谁的规律,即模型可接受;如果残差不是白噪声,说明还有部分信息没有被模型所识别,则剔除。
ACF自相关系数、PACF偏自相关函数可以帮助我们判断残差是否为白噪声,即该时间序列是否能被模型识别完全。

从上表可以看出,对残差进行Q检验得到的p值为0.451,即我们无法拒绝原假设,认为残差就是白噪声序列,因此简单季节性模型能够很好的识别本题中的机器人使用需求数据。
模型的比较与选择:使用平稳的R2或者AIC 和BIC准则。R2可以用来反应线性模型拟合的好坏,越接近于1拟合的越精准。加入的参数个数越多,模型拟合的效果越好,但这却是以提高模型复杂度为代价的(过拟合问题)。因此,模型选择要在模型复杂度与模型对数据的解释能力之间寻求最佳平衡。由于BIC对于模型的复杂程度的惩罚系数更大,BIC往往比AIC选择的模型更简洁,因此平稳的R2、BIC选小原则作为模型选择的参数。
BIC(贝叶斯信息准则)表达式如下:
B
I
C
=
l
n
(
T
)
(模型中参数个数)
−
2
l
n
(模型的极大似然函数)
(41)
BIC=ln(T)(模型中参数个数)-2ln(模型的极大似然函数) \tag{41}
BIC=ln(T)(模型中参数个数)−2ln(模型的极大似然函数)(41)
得出第31周的预测值:38、35、39、40、37、34、40。第32周前两天预测值:38、35。因此,得到未来某周第d天机器人需求数量矩阵,如下所示:
D
W
p
r
e
d
i
c
t
=
[
38
,
35
,
39
,
40
,
37
,
34
,
40
,
38
,
35
]
(42)
DWpredict=[38,35,39,40,37,34,40,38,35] \tag{42}
DWpredict=[38,35,39,40,37,34,40,38,35](42)
8.1.5 保障每天正常交付
为保障每天的机器人订单均已95%以上的概率交付,因此对机器人组装数量的约束条件进行修改,如下所示:
M
W
d
+
S
W
d
−
1
⩾
D
W
p
r
e
d
i
c
t
d
×
0.95
(43)
MW_{d}+SW_{d-1}\geqslant DW_{predict_d} \times 0.95 \tag{43}
MWd+SWd−1⩾DWpredictd×0.95(43)
8.1.6 保障整周正常交付
为保障整周的机器人订单均能以85% 以上的概率交付,因此作出如下约束:
∑
d
=
1
7
M
W
d
⩾
0.85
×
∑
d
=
1
7
D
W
p
r
e
d
i
c
t
d
(44)
\sum_{d=1}^7MW_d \geqslant 0.85 \times \sum_{d=1}^7DWpredict_d \tag{44}
d=1∑7MWd⩾0.85×d=1∑7DWpredictd(44)
值得注意的是,每天的订单均已95%以上的概率交付,则整周的机器人订单必定均能以85%以上的概率交付,即(44)式已暗含于(43)式。因此保证每天正常交付即可,即可以不考虑(43)式。
版权归原作者 每天都要写代码' 所有, 如有侵权,请联系我们删除。