聚类概述:
什么是聚类?
- 是把数据对象集合按照相似性划分成多个子集的过程。
- 每个子集是一个簇(cluster),分类的最终效果:使得簇中的对象彼此相似,但与其他簇中的对象相异。
- 聚类是无监督学习,因为给的数据没有类标号信息。
分类和聚类的区别
分类
- 有监督学习;
- 通过带标签的样本进行学习,生成分类模型(分类器)。 聚类
- 无监督学习;
- 通过观察学习,根据样本间的相似性将数据分割成多个簇。
基本聚类方法
- 划分方法
- 层次方法
- 基于密度的方法
划分方法
划分方法:将有n个对象的数据集D划分成k个簇,并且k≤n,满足如下的要求:
- 每个簇至少包含一个对象
- 每个对象属于且仅属于一个簇 基本思想:
- 首先创建一个初始k划分( k为要构造的划分数,即簇的个数);
- 然后不断迭代地计算各个簇的聚类中心,并依据新的聚类中心调整聚类情况,直至收敛。 目标:
- 同一个簇中的对象之间尽可能“接近”或相关;
- 不同簇中的对象之间尽可能“远离”或不同。 基于划分的方法实质上是一种启发式方法: k-均值(k-means)及其改进算法
- 每个簇用该簇中对象的均值来表示
- 基于质心的技术 k-中心点(k-medoids)算法
- 每个簇用接近簇中心的一个对象来表示
- 基于代表对象的技术 适用性方面:
- 适合中小规模数据库中的球状聚类;
- 对于大规模数据库和处理任意形状的聚类,这些算法需要进一步扩展。
K-Means算法

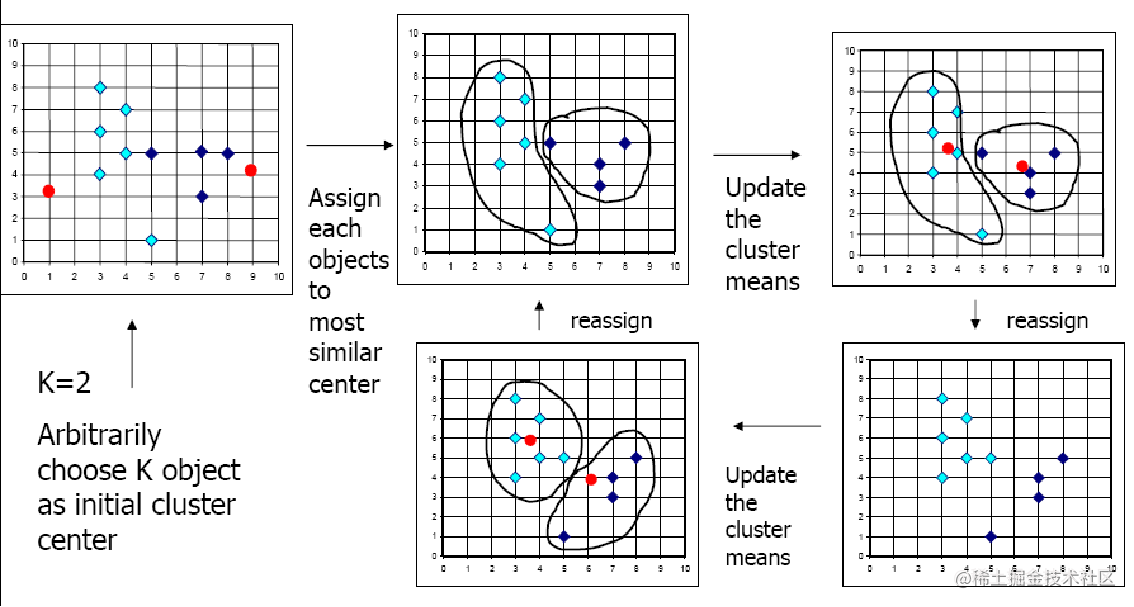
规定k=2,即划分为两个簇然后先随机选取两个红色的点作为聚类中心,然后通过计算其他点与中心点的距离来划分簇,当此次划分完成后通过计算均值来重新定义聚类中心,然后重复上述过程来重新划分簇.直到最后发现此次形成的簇与上一次相同,因此聚类过程到此结束。
Kmeans算法为启发式算法,遵循的寻优原则:
每次聚类保证局部最优,随后调整聚类,利用局部最优聚类的上限来不断逼近全局最优

K-Means算法优缺点
优点:
- 聚类时间快
- 当结果簇是密集的,而簇与簇之间区别明显时,效果较好
- 相对可扩展和有效,能对大数据集进行高效划分 缺点:
- 用户必须事先指定聚类簇的个数(即k值需指定)
- 常常终止于局部最优
- 只适用于数值属性聚类(计算均值有意义)
- 对噪声和异常数据也很敏感
- 不同的初始值,结果可能不同
- 不适合发现非凸面形状的簇凸面形状的簇–指圆形矩形等形状,是指当选择形状内任意两点,这两点的连线上所有点,也都在形状内。
K-Means算法还有一些改进算法:
- K-Mode算法
- K-Means++算法
K-Mode算法 —— 解决数据敏感的问题
在K-Means算法中只能适用于连续的数值属性的聚类,为解决离散属性的问题,K-Mode算法对其进行了改进:
- 用众数代替均值;
- 使用新的相异性度量方法。
K-Means++算法 —— 解决初始点选择问题
K-Means算法中初始值选择的不同也会引起不同的聚类结果,因此K-Means++算法对其做了改进。
K-Means++算法基本原理:
- 从输入的数据点集合中随机选择一个点作为第一个聚类中心;
- 对于数据集中的每一个点X,计算其与聚类中心的距离D(X);
- 选择一个D(X)最大的点作为新的聚类中心;
- 重复2和3步直到K个聚类中心被选出;
- 利用K个初始聚类中心运行K-Means算法。 *即尽可能选择距离远的点来作为初始种子节点
K-Mediods(K中心点算法)
K-Mediods算法可以解决K-Means算法对离群点敏感的问题。
K-中心点算法(解决对离群点敏感的问题):
- 选用簇中位置最中心的实际对象即中心点作为参照点;
- 基于最小化所有对象与其参照点之间的相异度之和的原则来划分(使用绝对误差标准)
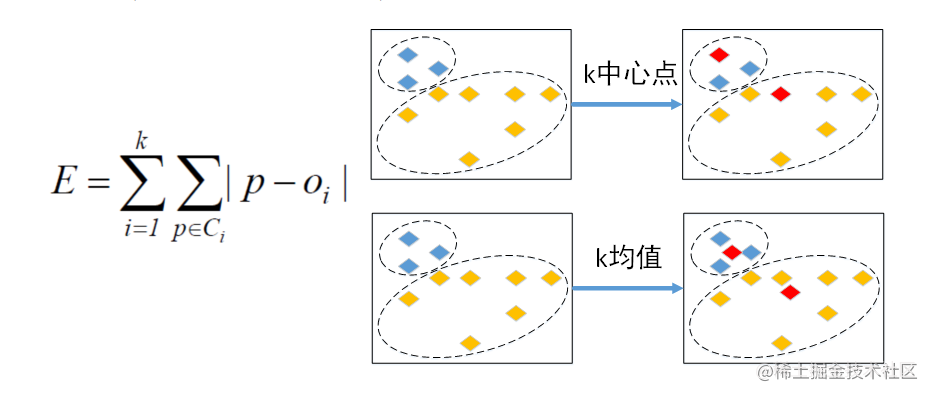
K-中心点算法的基本思想:
- 首先为每个簇随意选择一个代表对象,剩余的对象根据其与代表对象的距离分配给最近的一个簇。
- 然后迭代地用非代表对象来替代代表对象,以改进聚类的质量(找更好的代表对象)。
- 聚类结果的质量用一个代价函数来估算,该函数评估了对象与其参照对象之间的平均相异度。
PAM算法
PAM算法(Partitioning Around Medoids)是最早提出的K-中心点算法之一。
PAM算法的基本思想:
- 随机选择 k 个对象作为初始的代表对象;
- 指派每个剩余的对象给离它最近的代表对象所代表的簇;
- 随机地选择一个非代表对象Orandom;
- 计算用Orandom代替其中的代表对象Oj的总代价S ;
- 如果S<0,则用Orandom替换Oj形成新的k个代表对象的集合.


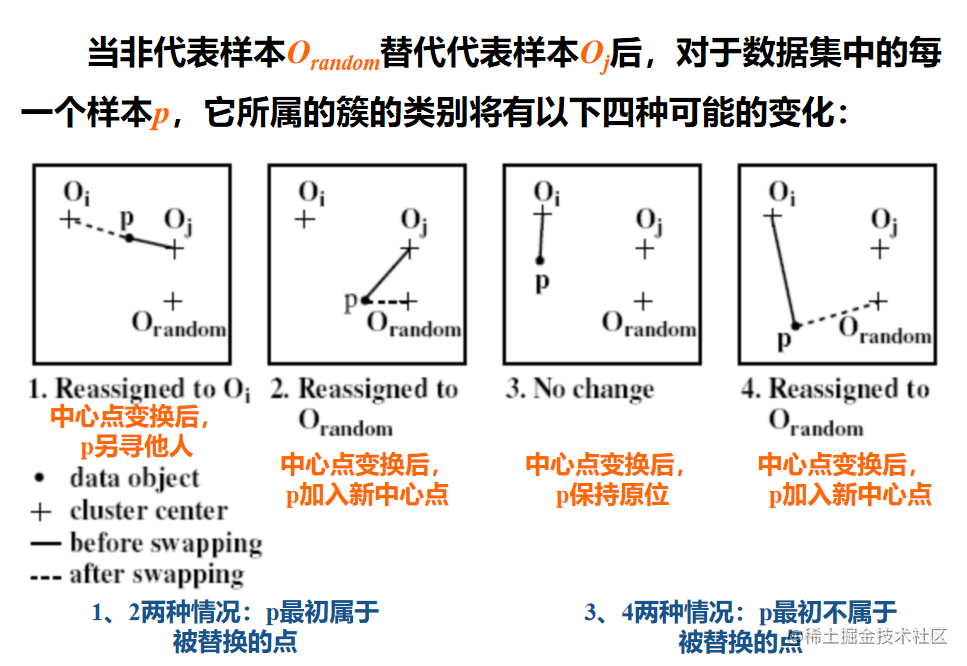
总而言之就是一个不断更新中心点使得总距离不断减小的过程.
PAM算法的优缺点
优点
- 当存在噪音和孤立点时,PAM 比K-Means算法更健壮。缺点
- PAM 对于较小的数据集非常有效,但不能很好地扩展到大型数据集,原因是计算复杂度较高。
- 每次中心点交换的时候,就要计算数据中每个点的代价

层次方法
层次方法需满足以下3个条件:
- 对给定数据对象集进行层次的分解;
- 使用距离矩阵作为聚类标准;
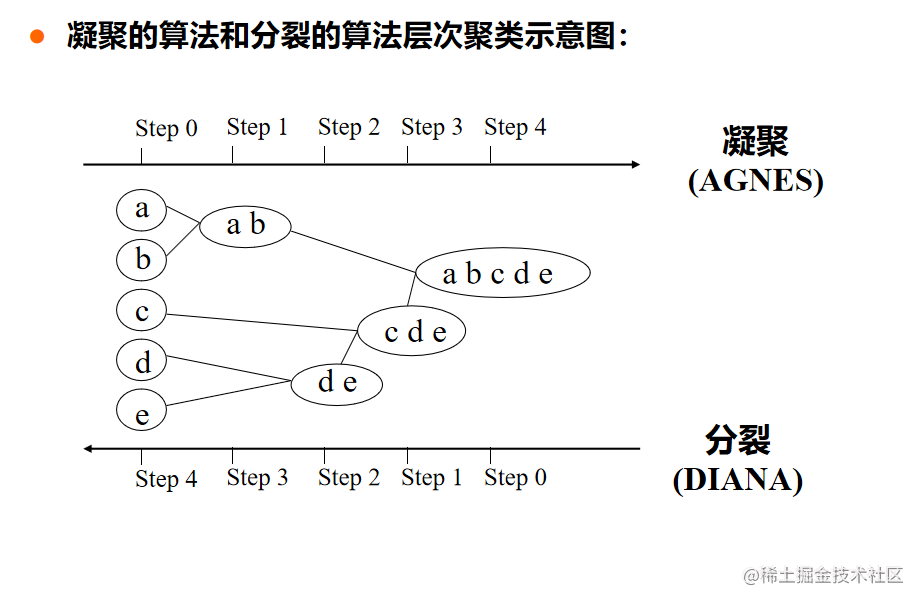
- 不需要输入聚类数目k,但需要终止条件。 两种层次方法:自底向上方法(凝聚)
- 初始将每个对象作为单独的一个簇,然后相继的合并相近的对象或簇,直到所有的簇合并为一个,或者达到一个终止条件。
- 代表算法:AGNES算法自顶向下方法(分裂)
- 初始将所有的对象置于一个簇中,在迭代的每一步,一个簇被分裂为多个更小的簇,直到最终每个对象在一个单独的簇中,或达到一个终止条件。
- 代表算法:DIANA算法
AGNES算法
- 首先,将数据集中的每个样本作为一个簇;
- 然后,根据某些准则将这些簇逐步合并;
- 合并的过程反复进行,直至不能再合并或者达到结束条件为止合并准则
- 每次找到距离最近的两个簇进行合并。
- 两个簇之间的距离由这两个簇中距离最近的样本点之间的距离来表示。计算距离有以下几种方法:
AGNES算法 —— 最小距离
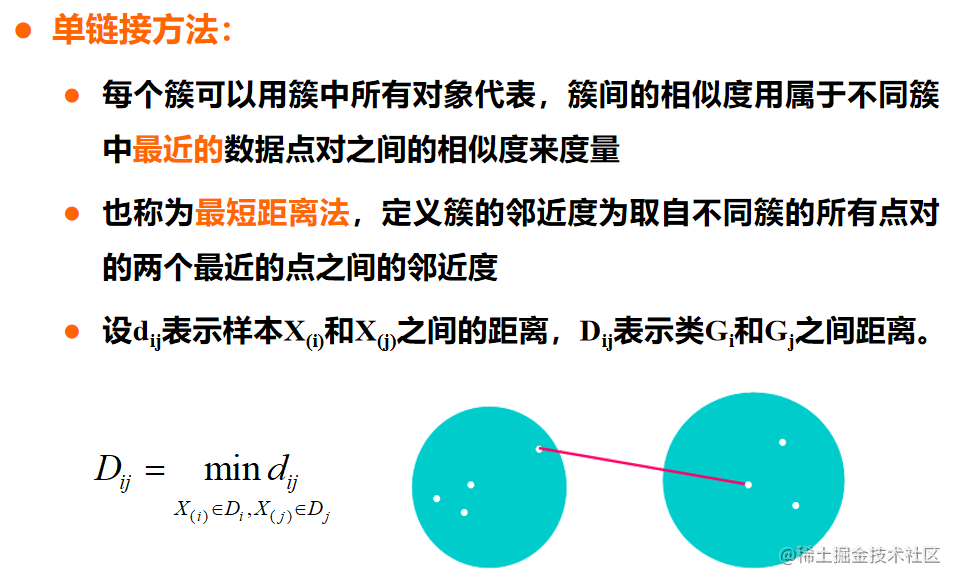
AGNES算法 —— 最大距离
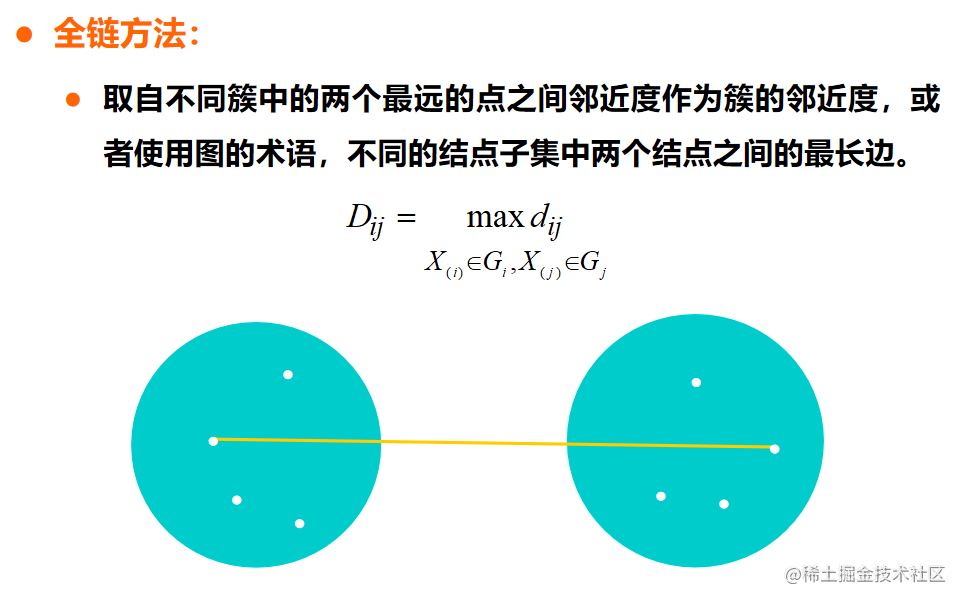
AGNES算法 —— 平均距离
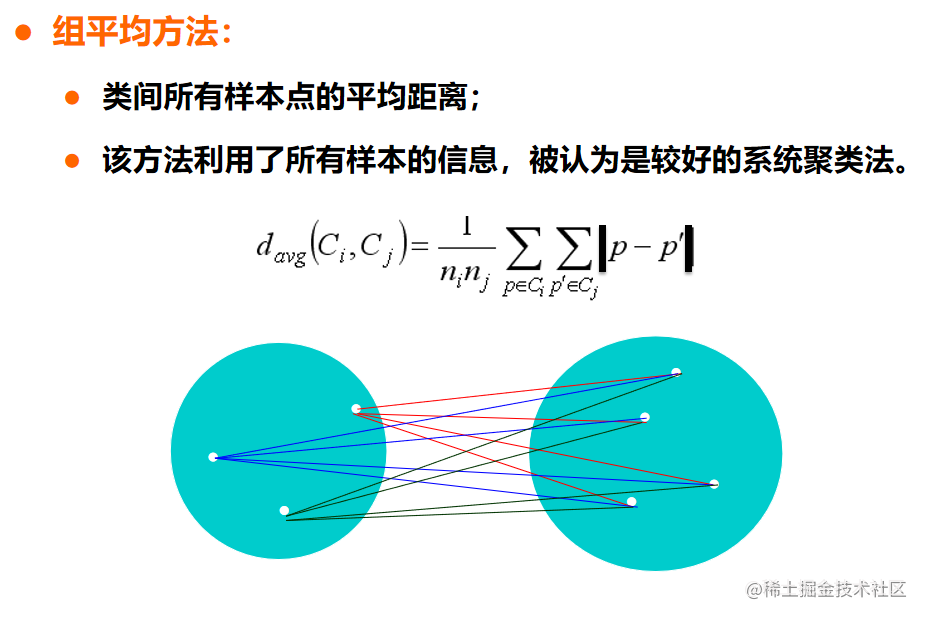
算法终止条件
(1)指定簇的数目k
(2)簇之间的距离超过一定阈值
DIANA算法
- 将所有的对象初始化到一个簇中。
- 在所有对象中找到最大距离的两个对象,对簇进行分类;
- 直到到达用户指定的簇数目或两个簇之间的距离超过某个阈值

即首先计算各个点到其他所有点的平均距离,选出最远的点作为新的簇,然后遍历旧的簇中所有点,计算他们分别和新旧两个簇中的最近点的距离,离谁更近就将它放入那个簇中.
层次方法的问题及改进
层次聚类存在的主要问题:
- 合并或分裂的决定需要检查和估算大量的对象或簇
- 一个步骤一旦完成便不能被撤销
- 避免考虑选择不同的组合,减少计算代价
- 不能更正错误的决定
- 不具有很好的可伸缩性改进方法:
- 将层次聚类和其他的聚类技术进行集成,形成多阶段聚类。
基于密度的方法
基于密度聚类方法:
- 根据密度条件对邻近对象分组形成簇,簇的增长或者根据邻域密度,或者根据特定的密度函数(只要临近区域的密度超过某个阈值,就继续聚类)主要特点:
- 发现任意形状的聚类
- 处理噪音
- 一遍扫描
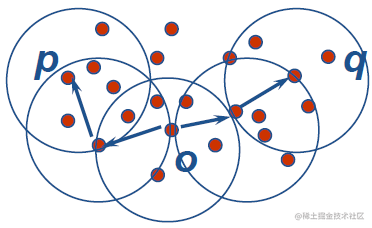
- 需要密度参数作为终止条件ε-邻域: 给定对象半径ε内的邻域称为该对象的ε-邻域。核心对象: 如果对象的ε-邻域至少包含最小数目MinPts个对象,则称该对象为核心对象直接密度可达: 给定对象集合D,如果 p 是在 q 的ε-邻域内,而 q 是核心对象,则称对象 p 是从对象 q 关于ε和MinPts直接密度可达的。密度可达: 如果存在一个对象链p1, …, pn,p1 = q, pn= p,使得pi+1是从pi直接密度可达的,则称对象p是从对象q关于ε和MinPts(间接)密度可达的。
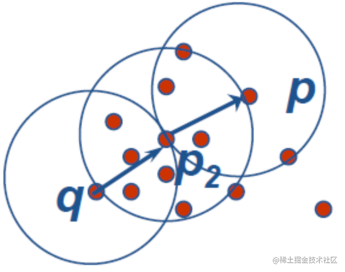
密度相连的:
如果存在对象 o ,使得p 和q 都是从o关于ε和MinPts密度可达的,则称对象p与q关于ε和MinPts是密度相连的.


聚类评估
聚类评估的任务:
- 估计聚类趋势:评估数据集是否存在非随机结构;
- 确定数据集中的簇数:在聚类之前,估计簇数;
- 测定聚类质量:聚类之后,评估结果簇的质量。
估计聚类趋势

确定数据集中的簇数
实验方法
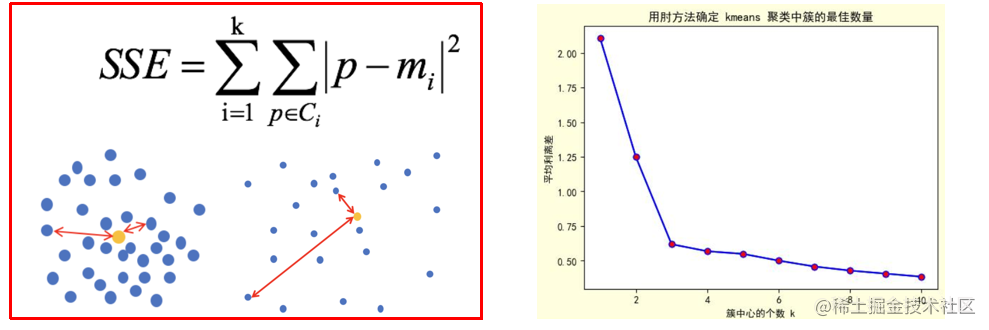
- 对于n个点的数据集,簇数√n/2,每个簇约有√2n个点。肘方法
- 增加簇数可以降低簇内方差之和,但是如果形成太多的簇,降低簇内方差之和的边缘效应可能下降。
测定聚类质量

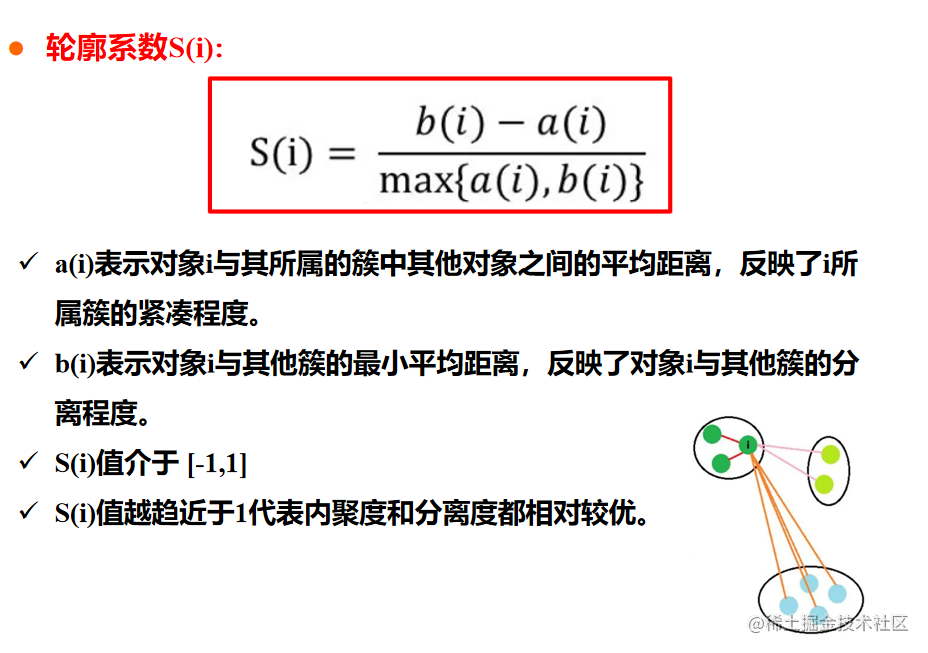
- 簇的同质性
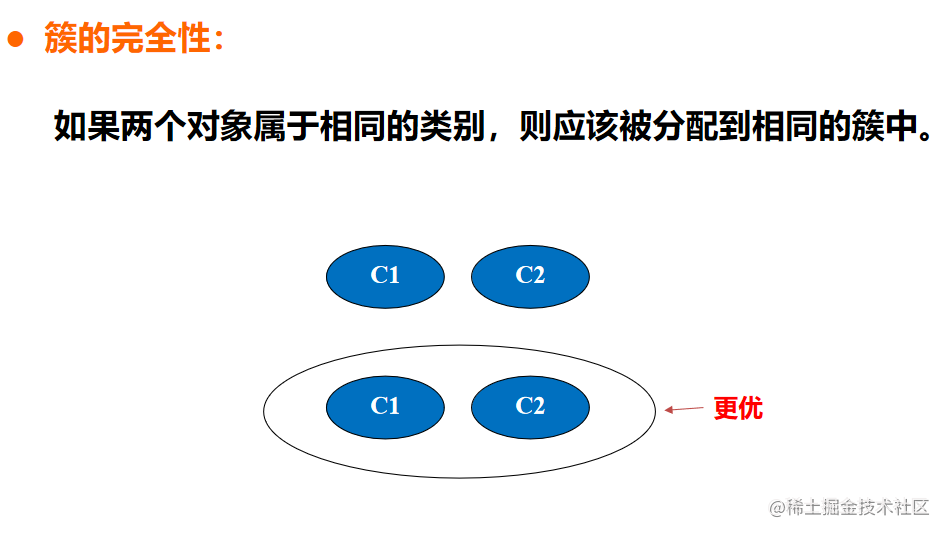
- 簇的完全性
- 碎布袋性
- 小簇保持性
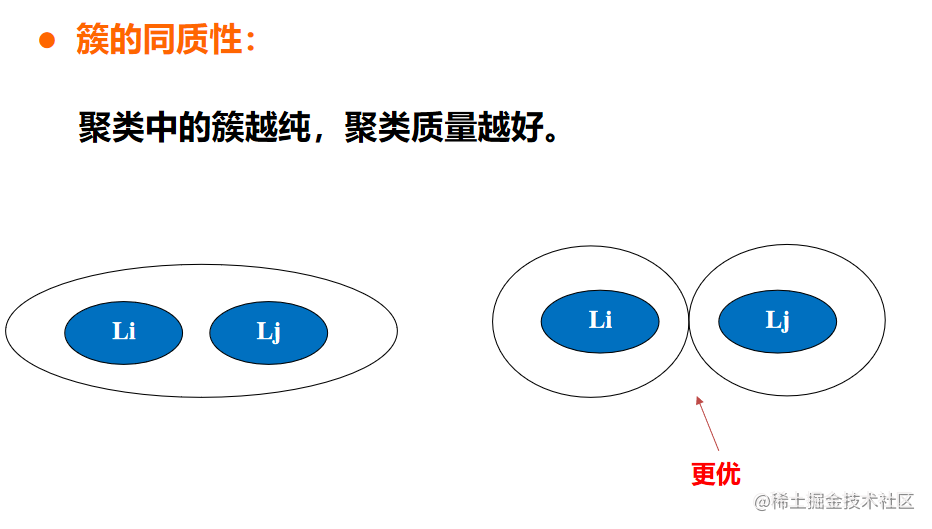
簇的同质性
簇的完全性
碎布袋性

小簇保持性

版权归原作者 冷月半明 所有, 如有侵权,请联系我们删除。