如果你是一名计算机专业的学生,有对图论有基本的了解,那么你一定知道一些著名的最优路径解,如Dijkstra算法、Bellman-Ford算法和a*算法(A-Star)等。
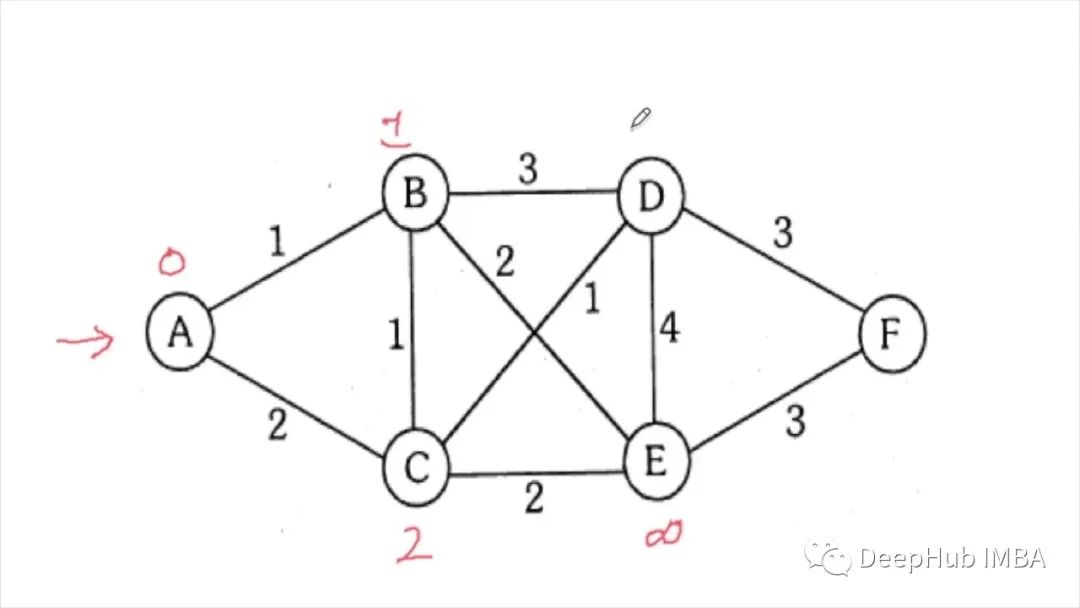
这些算法都是大佬们经过无数小时的努力才发现的,但是现在已经是人工智能的时代,强化学习算法能够为我们提出和前辈一样好的解决方案吗?
本文中我们将尝试找出一种方法,在从目的地a移动到目的地B时尽可能减少遍历路径。我们使用自己的创建虚拟数据来提供演示,下面代码将创建虚拟的交通网格:
importnetworkxasnx
# Create the graph object
G=nx.Graph()
# Define the nodes
nodes= ['New York, NY', 'Los Angeles, CA', 'Chicago, IL', 'Houston, TX', 'Phoenix, AZ', 'Dallas, TX', 'Miami, FL']
# Add the nodes to the graph
G.add_nodes_from(nodes)
# Define the edges and their distances
edges= [('New York, NY', 'Chicago, IL', {'distance': 790}),
('New York, NY', 'Miami, FL', {'distance': 1300}),
('Chicago, IL', 'Dallas, TX', {'distance': 960}),
('Dallas, TX', 'Houston, TX', {'distance': 240}),
('Houston, TX', 'Phoenix, AZ', {'distance': 1170}),
('Phoenix, AZ', 'Los Angeles, CA', {'distance': 380}),
('Los Angeles, CA', 'Dallas, TX', {'distance': 1240}),
('Los Angeles, CA', 'Chicago, IL', {'distance': 2010})]
# Add the edges to the graph
G.add_edges_from(edges)
运行起来没有报错,但是我们不知道数据是什么样子的,所以让我们先进行可视化,了解数据:
importmatplotlib.pyplotasplt
# set positions for the nodes (optional)
pos=nx.spring_layout(G)
# draw the nodes and edges
nx.draw_networkx_nodes(G, pos, node_color='lightblue', node_size=500)
nx.draw_networkx_edges(G, pos, edge_color='gray', width=2)
# draw edge labels
edge_labels=nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
# draw node labels
node_labels= {node: node.split(',')[0] fornodeinG.nodes()}
nx.draw_networkx_labels(G, pos, labels=node_labels)
# show the plot
plt.axis('off')
plt.show()
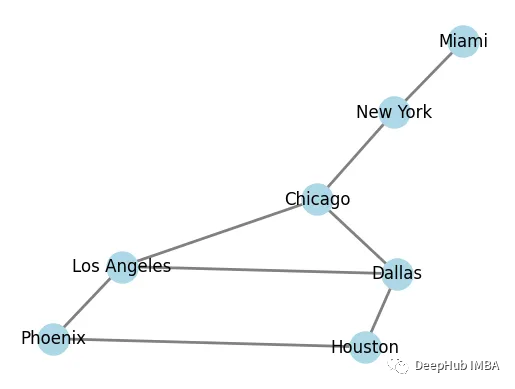
我们有了一个基本的节点网络。但是这感觉太简单了。对于一个强化学习代理来说,这基本上没有难度,所以我们增加更多的节点:
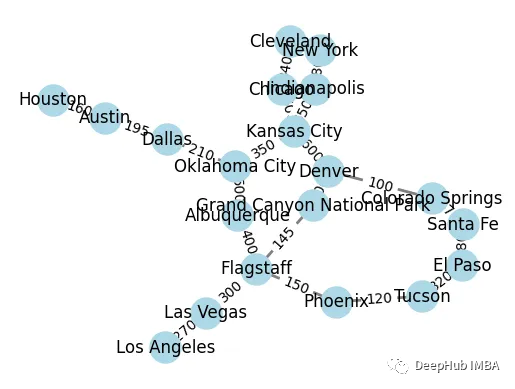
这样就复杂多了,但是它看起来很混乱,比如从New York 到 Arizona就可能是一个挑战。
我们这里使用最常见且通用的Q-Learning来解决这个问题,因为它有动作-状态对矩阵,可以帮助确定最佳的动作。在寻找图中最短路径的情况下,Q-Learning可以通过迭代更新每个状态-动作对的q值来确定两个节点之间的最优路径。
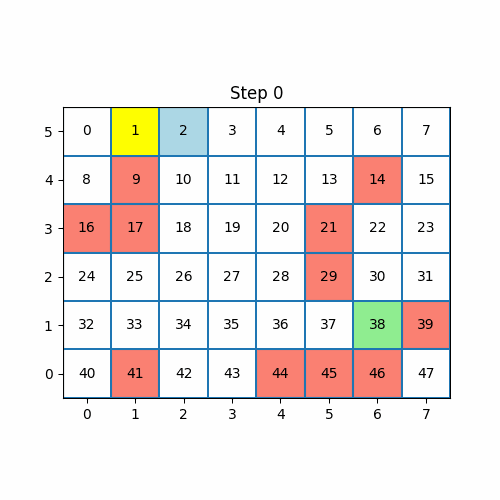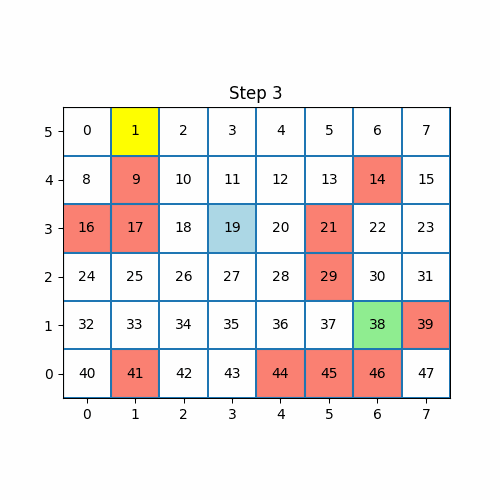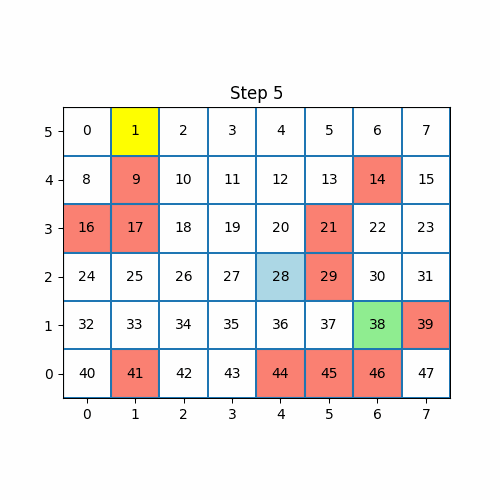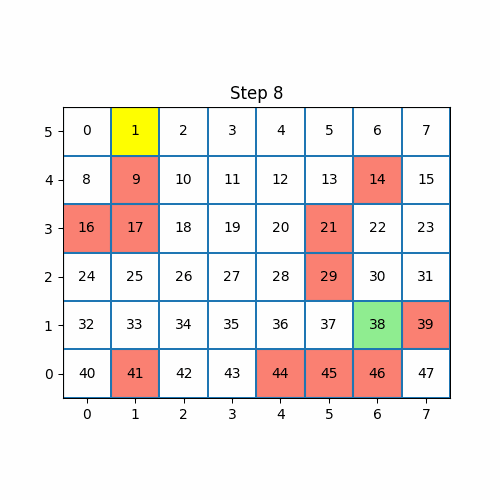
上图为q值的演示。
下面我们开始实现自己的Q-Learning
importnetworkxasnx
importnumpyasnp
defq_learning_shortest_path(G, start_node, end_node, learning_rate=0.8, discount_factor=0.95, epsilon=0.2, num_episodes=1000):
"""
Calculates the shortest path in a graph G using Q-learning algorithm.
Parameters:
G (networkx.Graph): the graph
start_node: the starting node
end_node: the destination node
learning_rate (float): the learning rate (default=0.8)
discount_factor (float): the discount factor (default=0.95)
epsilon (float): the exploration factor (default=0.2)
num_episodes (int): the number of episodes (default=1000)
Returns:
A list with the shortest path from start_node to end_node.
"""
我们的输入是整个的图,还有开始和结束的节点,首先就需要提取每个节点之间的距离,将其提供给Q-learning算法。
# Extract nodes and edges data
nodes=list(G.nodes())
num_nodes=len(nodes)
edges=list(G.edges(data=True))
num_edges=len(edges)
edge_distances=np.zeros((num_nodes, num_nodes))
fori, j, datainedges:
edge_distances[nodes.index(i), nodes.index(j)] =data['weight']
edge_distances[nodes.index(j), nodes.index(i)] =data['weight']
创建一个Q-table ,这样我们就可以在不断更新模型的同时更新值。
# Initialize Q-values table
q_table=np.zeros((num_nodes, num_nodes))
# Convert start and end node to node indices
start_node_index=nodes.index(start_node)
end_node_index=nodes.index(end_node)
下面就是强化学习算法的核心!
# Q-learning algorithm
forepisodeinrange(num_episodes):
current_node=start_node_index
print(episode)
whilecurrent_node!=end_node_index:
# Choose action based on epsilon-greedy policy
ifnp.random.uniform(0, 1) <epsilon:
# Explore
possible_actions=np.where(edge_distances[current_node,:] >0)[0]
iflen(possible_actions) ==0:
break
action=np.random.choice(possible_actions)
else:
# Exploit
possible_actions=np.where(q_table[current_node,:] ==np.max(q_table[current_node,:]))[0]
iflen(possible_actions) ==0:
break
action=np.random.choice(possible_actions)
# Calculate reward and update Q-value
next_node=action
reward=-edge_distances[current_node, next_node]
q_table[current_node, next_node] = (1-learning_rate) *q_table[current_node, next_node] +learning_rate* (reward+discount_factor*np.max(q_table[next_node, :]))
# Move to next node
current_node=next_node
ifcurrent_node==end_node_index:
break
print(q_table)
这里需要注意的事情是,我们鼓励模型探索还是利用一个特定的路径。
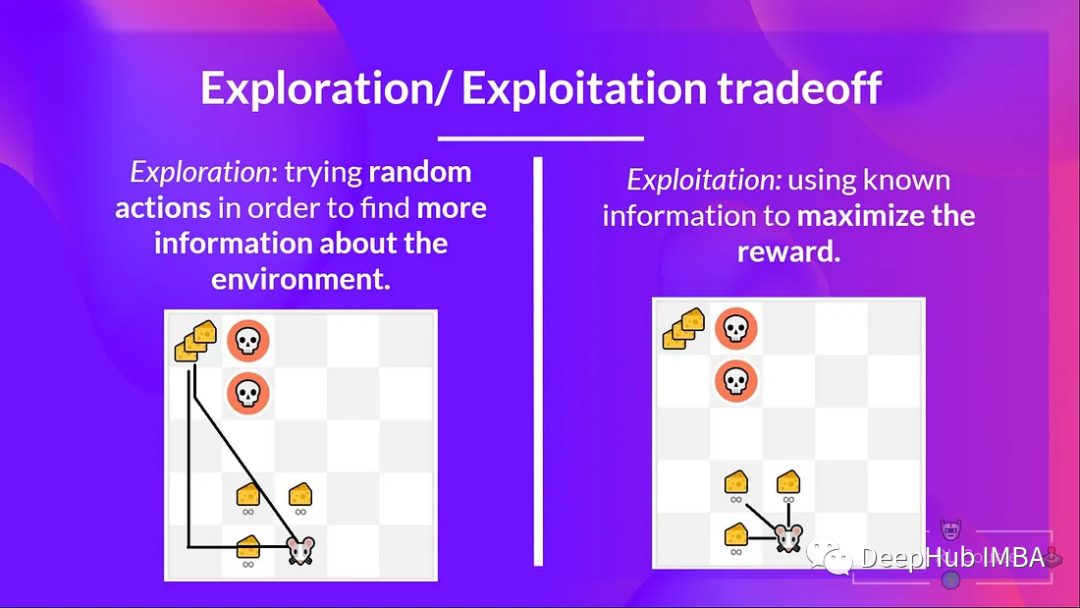
大多数强化算法都是基于这种简单的权衡制定的。 过多的探索的问题在于它可能导致代理花费太多时间探索环境,而没有足够的时间利用它已经学到的知识,可能导致代理采取次优行动并最终无法实现其目标。 如果探索率设置得太高,代理可能永远不会收敛到最优策略。但是如果探索率设置得太低,代理可能会陷入次优策略。 所以,需要在探索和利用之间取得平衡,确保代理进行足够的探索以了解环境,同时利用其知识来最大化回报。

而强化学习中过多利用的问题会使代理陷入次优策略,无法发现可能更好的动作或状态。 即使有更好的选择,代理也可能对其当前的政策过于自信。 这被称为“漏洞利用陷阱”或“局部最优”问题,代理无法从次优解决方案中逃脱。 在这种情况下,探索有助于发现更好的策略和避免“局部最优”。
回到我们的代码,我们需要检查Q-table ,并确保可以从中提取出最短路径。
# Extract shortest path from Q-values table
shortest_path= [start_node]
current_node=start_node_index
whilecurrent_node!=end_node_index:
next_node=np.argmax(q_table[current_node, :])
shortest_path.append(nodes[next_node])
current_node=next_node
shortest_path.append(end_node)
returnshortest_path
最后,使用函数来检查否能够得到所需的输出。
shortest_path=q_learning_shortest_path(G, 'New York, NY', 'Phoenix, AZ')
print(shortest_path)
输出结果如下:

这就是我们数据中从New York, NY到Phoenix, AZ的最短路径!
如果你感兴趣或者想了解更多,可以在这个链接中查看完整的代码。
https://github.com/amos-eda-97/Q-learning-based-optimal-path
作者:Amos Eda