Speecher: Bingsheng Zhang
这一系列的课程,为了介绍一些基础,弥补一些上密码学课和看论文的Gap。
历史上的密码学是art,就像鲁班锁,看着很精妙,但是没有证明。
1970s以来,逐渐发展成Science。
定义和模型一直在改,但是方法论和安全性证明是一样的。
传统的应用:
- 机密性(加密)
- 完整性(MAC)
- 验证(签名)
现代的原语:
- 区块链
- FHE
- ZK
- SMPC
- ABE
- functional encryption
- indistinguishability obfuscation
现代密码学的核心准则:可证明安全。主要分为三步:
- 准确地定义威胁模型,即:什么是安全? - “什么是安全”的正式模型和定义,比如敌手能做什么、不能做什么…
- 提出构造 - 算法、协议、scheme
- 写一个正式的proof(在这系列课程中,基本就是reduction) - 在什么样的威胁模型下,如果某个假设成立,那么构造是安全的(除了极少数的,比如one-time-pad,都会有假设,即使one-time-pad,也会对随机性有假设)。- 假设的说明要清晰、没有歧义。
最后我们会得到四个东西:
- 安全性定义
- 假设
- 协议
- 证明
可证明安全最后也可能不安全:你的假设可能被攻破、威胁模型可能和实际不同(就像你锁了门,但是没关窗)。
1976:DH密钥协商(HTTPS-TLS-DH),这一次我们将部分涉及DH的安全性。为什么DH是安全的?基于什么(假设)是怎么样安全的?
1977:RSA(比如用于电子护照的签名)。
我们以DH介绍可证明安全的初步。
Zhang:一般自己别造假设,follow一些经典假设就够了,否则,虽然也叫可证明安全,但是会被challenge,因为自己对密码学领域的理解并没有那么牛逼。但是,密码学界的一些新突破,比如Gentry(2009)的FHE,就假设了理想格,给了一个构造。但是分析这个假设就可以出三大密。
Textbook RSA 是不安全的
Textbook RSA:就是RSA在课本里呈现的形态,选个
P
,
Q
P,Q
P,Q,乘起来、再构造公钥私钥blabla。
Textbook RSA它并不是一个加密算法,而是一个带陷门的one-way permutation。
几年前,有人发现QQ浏览器用的Textbook RSA进行加密,于是写了一篇文章批判一番。
后期,很多学校课程都在说Textbook RSA在各种情况下是不安全的。那RSA怎么用呢?
比如说,加PKCS1.5的padding。RSA本身不是公钥加密算法,
我们给明文加padding,再做一个trapdoor one-way permutation,这就成了一个加密算法。
至于这个算法怎么安全,比如CPA/CCA安全,这就看具体的padding方法和proof。
Warm-up:单向函数(One-way function)
密码学中最基础的一个假设:假设单向函数存在。
实际上,我们不知道单向函数是不是真的存在。
(更事实上地,整个现代密码学的基础就基于假设)
函数
f
:
{
0
,
1
}
n
→
{
0
,
1
}
m
f: \{0,1\}^n \rightarrow \{0,1\}^m
f:{0,1}n→{0,1}m是单向的,如果有:
∀ x , f ( x ) \forall x, f(x) ∀x,f(x)是多项式时间可计算的。- 难以反向:对于所有的概率多项式时间(probabilistic polynomial-time, PPT)算法 A \mathcal A A,有 P [ I n v e r t A , f ( n ) = 1 ] < ϵ ( n ) P[Invert_{\mathcal A, f}(n) = 1] < \epsilon(n) P[InvertA,f(n)=1]<ϵ(n) (换句话说,玩下面这个Game时,赢的概率可以忽略)
其中
ϵ
\epsilon
ϵ是一个negligible函数,
n
n
n在此定义为安全参数。
其中,
I
n
v
e
r
t
A
,
f
(
n
)
Invert_{\mathcal A, f}(n)
InvertA,f(n)是一个game,包含以下四步:
- 选择随机 x ← { 0 , 1 } n x \leftarrow {0,1}^n x←{0,1}n
- 计算 y = f ( x ) y=f(x) y=f(x)
- 获取 x ′ ← A ( 1 n , y ) x' \leftarrow \mathcal A(1^n, y) x′←A(1n,y)(给敌手 y y y和安全参数,让它选择 x ′ x' x′)
- 当且仅当 f ( x ′ ) = y f(x') = y f(x′)=y时返回1(win)
关于game:
game有一个challenge(考官)和一个adversary(考生)。考官出一些题来考试(play game),通过表现来判断考试是否通过。
为什么说game是考试呢?因为规定了能力(考生能看见什么不能看见什么)、时间(多项式时间)etc
注意一些细节:
A \mathcal A A不要求回答一个完全正确的 x x x,只要回答一个原像 x ′ x' x′就OK。x x x要在足够大的域里选(安全参数规定的域里选)。
一个等价的定义:
P
x
←
{
0
,
1
}
n
[
A
(
1
n
,
f
(
x
)
)
∈
f
−
1
(
f
(
x
)
)
]
≤
ϵ
(
n
)
P_{x \leftarrow \{0,1\}^n}[\mathcal{A}(1^n, f(x)) \in f^{-1}(f(x))]\leq \epsilon(n)
Px←{0,1}n[A(1n,f(x))∈f−1(f(x))]≤ϵ(n)
但是绝大多数的game很难这么简洁地写,因为很多game的操作很复杂,在一行里写清楚可能性不大。
一些练习。假设
f
(
x
)
f(x)
f(x)是一个安全的单向函数,那么
f ( m ) f(m) f(m)能不能做 m m m的一个one way commitment?
不能。它的问题是:
f
(
x
)
f(x)
f(x)是单向函数的话,要求
x
←
{
0
,
1
}
n
x \leftarrow \{0,1\}^n
x←{0,1}n,但是这里
m
m
m没说是uniformly random的。比如石头剪刀布,plaintext的选项只有三种可能性,我们不会拿
m
m
m做commitment,因为它就没有hiding的性质——试一试
f
(
剪刀
)
f(剪刀)
f(剪刀)、
f
(
石头
)
f(石头)
f(石头)、
f
(
布
)
f(布)
f(布)就什么都知道了。
在微信对话框里如何在不引入可信第三方的情况下相互(公平地)玩石头剪刀布?这就要用到commitment。
f ( m ∣ ∣ r ) f(m||r) f(m∣∣r)是不是 m m m的一个commitment?其中 r ← { 0 , 1 } 256 r \leftarrow \{0,1\}^{256} r←{0,1}256、 m ∣ ∣ r m||r m∣∣r是concatenate操作。答案是否定的。根据前面game的定义,不能exactly找到 x x x,但是这个game没说不能精确找到其中的哪些位。
同样的scheme,你用不同的假设(比如把上述game中的one-way function 换成 random oracle),有的时候能做出来,有的时候做不出来。
离散对数问题(一般基于一个group generator
G
\mathcal G
G)
这个
G
\mathcal G
G,你给它一个安全参数,它就生成一个群并返回。
但是在现实中不是这么用的。你自己生成一个security group,审稿人不一定认。现实中大家一般用公开的group,比如椭圆曲线。
设
G
\mathcal G
G是一个通用的、多项式时间的、群生成算法。那么向
G
\mathcal G
G 传入安全参数
1
n
1^n
1n,生成一个循环群
G
\mathbb G
G(乘群),输出
G
\mathbb G
G的阶
q
q
q,
q
q
q的位数是
n
n
n,一个生成元
g
∈
G
g \in \mathbb G
g∈G。
离散对数假设
D
L
o
g
A
,
G
(
n
)
DLog_{\mathcal{A,G}}(n)
DLogA,G(n)如下:
- 生成 ( G , q , g ) ← G ( 1 n ) (\mathbb G, q, g) \leftarrow \mathcal G(1^n) (G,q,g)←G(1n)
- 随机选取 h ← G h \leftarrow \mathcal G h←G(这一步隐含这个群应该是efficiently samplable,当然不这么做也行,可以选取一个 y y y,返回 g y ← G g^y \leftarrow \mathcal G gy←G)
- 采样 x ← A ( G , q , g , h ) x \leftarrow \mathcal A(\mathbb G, q, g, h) x←A(G,q,g,h)
- 当且仅当 g x = h g^x = h gx=h时返回1
我们说DL问题(关于
G
\mathcal G
G)是困难的,如果对于所有的PPT 算法
A
\mathcal A
A:
∣
P
[
D
L
o
g
G
,
A
(
n
)
=
1
]
−
1
/
q
∣
≤
ϵ
(
n
)
|P[DLog_{\mathcal{G, A}}(n) = 1] - 1/q| \leq \epsilon(n)
∣P[DLogG,A(n)=1]−1/q∣≤ϵ(n)
其中:
1 / q 1/q 1/q是默认的取胜概率(即瞎猜)。- 为什么加绝对值呢?因为全猜错也是一种本事(
问题:(非交互式的,Non-Interactive)DH密钥交换(DiffieHellmanKeyExchange)(NIKE)是安全的吗?
这个问题正确的问法是:DHKE在假设X下是Y安全的吗?(这里,我们认为NIKE和DHKE是一个东西)。
于是有三个任务:
- 正式定义非交互式KE的安全性(即Y安全)
- 确定X
- 基于归约给出证明(X成立则达到Y安全性)
首先,如下图所示,我们来简要地看下DH的过程。记左为Alice,右为Bob,那么最基础版本DH的步骤如下:![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8D7wDGAi-1690098418516)(image.png)]](https://img-blog.csdnimg.cn/b2130c2afa834bf1a58d2f3f24061df6.png)
- 双方协商大素数 P P P和生成元 g g g,并且共同持有它们
- Alice生成私钥 s s s和公钥 h = g s m o d P h = g^s \mod P h=gsmodP,将 h h h发给Bob
- Bob生成私钥 t t t和公钥 f = g t m o d P f = g^t \mod P f=gtmodP,将 f f f发给Alice
此时,Alice已知
P
,
g
,
s
,
h
,
f
P, g, s, h, f
P,g,s,h,f,Bob已知
P
,
g
,
t
,
h
,
f
P, g, t, h, f
P,g,t,h,f。
- Alice计算密钥 k e y = f s key = f^s key=fs,Bob计算密钥 k e y = h t key = h^t key=ht
在上图中,攻击者是中间的人。攻击者能做什么?攻击者要做什么?这里假设攻击者只能看交互的信息,其他的什么都做不了(虽然实际上攻击者可以做中间人攻击)。攻击者要猜测
k
e
y
=
g
s
t
key=g^{st}
key=gst。
根据上面的intuition,我们给出下面的NIKE的Key-Recovery(KR)安全性定义:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-n92YEHgd-1690098418517)(image-1.png)]](https://img-blog.csdnimg.cn/1e3ee917e1e845bd9f7f492de8c5ae1b.png)
我们要证明DH NIKE是KR安全的。![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UaPOMtfw-1690098418517)(image-2.png)]](https://img-blog.csdnimg.cn/1c4407d9c67d4513ac09a24ee0e4cf9a.png)
看上面的图,图里的各种线展示了一个攻击者可能攻击的途径。见问号处,给定
g
s
,
g
t
g^s, g^t
gs,gt,为什么到不了
g
s
t
g^{st}
gst?需要注意,它并不是DL假设能说通的。
DH文章中介绍了一个tautological assumption(永真式)——CDH,作为安全性假设。

DHKE是KR安全的,因为CDH假设。
原因如下:
定理. 如果CDH是安全的,那么DL是安全的。
证明思路. 使用反证法。如果攻击者可以破解DL,那么攻击者可以破解CDH。蕴含了一个安全性归约。
于是,下面这张图中可见的攻击方法都被封堵了: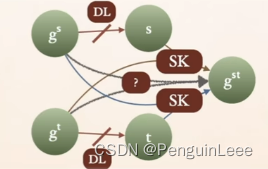
DL的安全性由CDH安全的永真式保证,问号处的安全性由假设保证,sk处的安全性由私钥的保密性推出。
Appendix
关于PPT algorithms![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uP3uL4TC-1690098418518)(image-4.png)]](https://img-blog.csdnimg.cn/69fdc743b761498a9f4756aa585c69ff.png)

版权归原作者 PenguinLeee 所有, 如有侵权,请联系我们删除。