在前三部分中我们介绍了CUDA开发的大部分基础知识,例如启动内核来执行并行任务、利用共享内存来执行快速归并、将可重用逻辑封装为设备函数以及如何使用事件和流来组织和控制内核执行。
本文是本系列的最后一部分,我们将讨论原子指令,它将允许我们从多个线程中安全地操作同一内存。我们还将学习如何利用这些操作来创建互斥锁,互斥锁是一种编码模式,它允许我们“锁定”某个资源,以便每次只由一个线程使用它。可以说这两个概念是任何多线程的基础。
还是从头开始,我们导入和加载库,并确保有一个GPU。
import warnings
from datetime import datetime
from time import perf_counter
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import numpy as np
import requests
import numba
from numba import cuda
from numba.core.errors import NumbaPerformanceWarning
from tqdm.auto import trange
print(np.__version__)
print(numba.__version__)
print(mpl.__version__)
# Ignore NumbaPerformanceWarning
warnings.simplefilter("ignore", category=NumbaPerformanceWarning)
# 1.21.6
# 0.56.2
# 3.5.3
# Found 1 CUDA devices
# id 0 b'Tesla T4' [SUPPORTED]
# Compute Capability: 7.5
# PCI Device ID: 4
# PCI Bus ID: 0
# UUID: GPU-53ffb366-a0f2-a5b0-315a-18d00573d9ba
# Watchdog: Disabled
# FP32/FP64 Performance Ratio: 32
# Summary:
# 1/1 devices are supported
# True
原子操作
GPU编程的思想是基于尽可能多地并行执行相同的指令。对于许多可以并行任务,线程之间不需要合作或使用其他线程使用的资源,只要保证自己运行正确即可。但是一些需要同步执行的操作,例如归并(Reduce),需要通过算法的设计确保相同的资源只被线程的子集使用,所以需要通过使用同步线程确保所有其他线程都是最新的。
在某些情况下,多个线程必须对同一个数组进行读写。当试图同时执行读或写操作时,这可能会导致问题,例如假设我们有一个将一个值加1的内核。
# Example 4.1: A data race condition.
@cuda.jit
def add_one(x):
x[0] = x[0] + 1
当我们用一个线程块启动这个内核时,我们将在输入数组中存储一个值1。
dev_val = cuda.to_device(np.zeros((1,)))
add_one[1, 1](dev_val)
dev_val.copy_to_host()
# array([1.])
如果我们启动10个区块,每个区块有16个线程时会发生什么?10 × 16 × 1加到同一个内存元素中,所以我们应该希望dev_val中得到的值是160。对吧?
dev_val = cuda.to_device(np.zeros((1,)))
add_one[10, 16](dev_val)
dev_val.copy_to_host()
如果使用上面的操作,我们不太可能在dev_val中得到到160。为什么呢?因为线程同时在读写同一个内存变量!
下面是当四个线程试图从同一个全局内存中读写时可能发生的情况的示意图。线程1-3从全局寄存器读取相同的值0的次数不同(t分别为0,2,2)。它们都增加1,并在t= 4,7和8时写回全局内存。线程4开始的时间比其他线程稍晚,在t=5时。此时,线程1已经写入全局内存,因此线程4读取的值为1。它最终会在t=12时将全局变量改写为2。
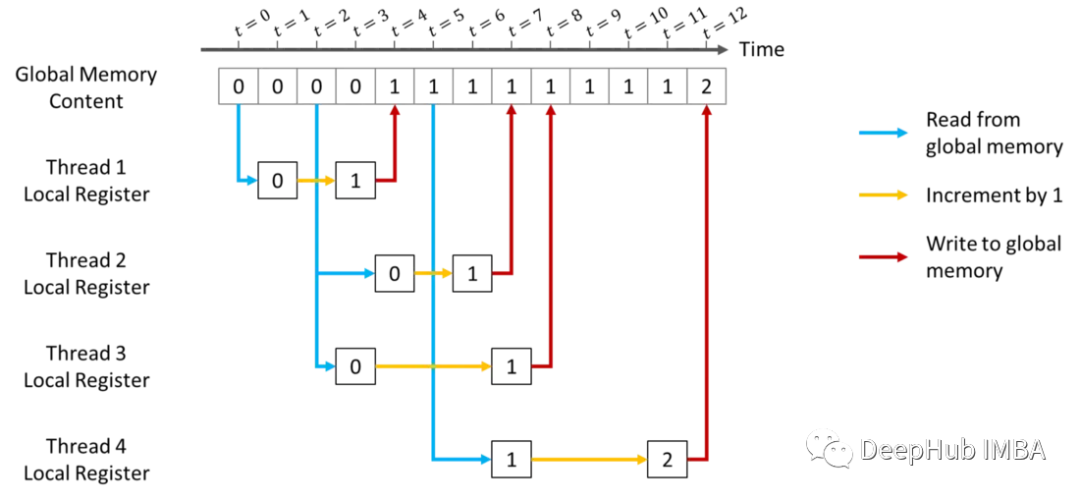
从同一个全局内存中读写的多个线程的情况示意图,也就是说这个操作是非线程安全的
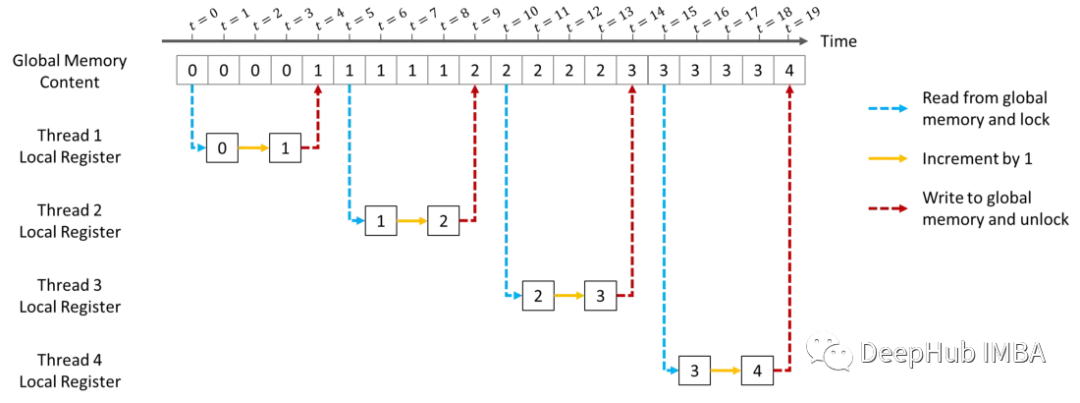
当一个线程对内容进行操作时,资源被禁止读/写,所以确保每个线程在读时获得更新的值,而其他线程看到它的写。这种线程安全的操作通常较慢。
如果我们想要获得最初期望的结果(如图2所示),我们应该用原子操作(上面的线程安全的操作)替换非原子加法操作。原子操作将确保无论读/写的是什么内存,每次都由单个线程完成。
# Example 4.2: An atomic add without race conditions.
@cuda.jit
def add_one_atomic(x):
cuda.atomic.add(x, 0, 1) # Arguments are array, array index, value to add
dev_val = cuda.to_device(np.zeros((1,)))
add_one_atomic[10, 16](dev_val)
dev_val.copy_to_host()
# array([160.])
原子加法操作示例:计算直方图
为了更好地理解在哪里以及如何使用原子操作,我们将使用直方图计算。假设有人想数一数在某一文本中字母表中的每个字母有多少个。实现这一目标的一个简单算法是创建26个“桶”,每个桶对应英语字母表中的一个字母。然后我们将遍历文本中的字母,每当我们遇到“a”时,我们将增加第一个bucket 1,每当我们遇到“b”时,我们将增加第二个bucket 1,以此类推。
在标准Python中,可以使用字典来实现我们的“桶”,每个字典都将一个字母与一个数字联系起来。由于我们是在GPU上进行操作,所以这里将使用数组代替字典,并且将存储所有 128 个 ASCII 字符,而不是存储 26 个字母。
在此之前,我们需要将字符串转换为“数字”数组。在这种情况下可以将UTF-8字符串转换为uint8数据类型。
def str_to_array(x):
return np.frombuffer(bytes(x, "utf-8"), dtype=np.uint8)
def grab_uppercase(x):
return x[65 : 65 + 26]
def grab_lowercase(x):
return x[97 : 97 + 26]
my_str = "CUDA by Numba Examples"
my_str_array = str_to_array(my_str)
# array([ 67, 85, 68, 65, 32, 98, 121, 32, 78, 117, 109, 98, 97,
# 32, 69, 120, 97, 109, 112, 108, 101, 115], dtype=uint8)
小写字母和大写字母有不同的代码。我们将用函数来实现仅选择小写字母或仅选择大写字母。
并且Numpy已经提供了一个直方图函数,我们将使用它来验证结果并比较运行时。
histo_np, bin_edges = np.histogram(my_str_array, bins=128, range=(0, 128))
np.testing.assert_allclose(bin_edges, np.arange(129)) # Bin edges are 1 more than bins
def plot_letter_histogram(hist, bin_edges, kind="percent", ax=None):
width = 0.8
start = bin_edges[0]
stop = bin_edges[0] + hist.shape[0]
if ax is None:
ax = plt.gca()
ax.bar(np.arange(start, stop), hist, width=width)
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.xaxis.set_major_formatter(ticker.FuncFormatter(lambda x, pos: f"{int(x):c}"))
ax.set(xlim=[start - width, stop - 1 + width], ylabel=kind.title())
if kind == "count":
ax.yaxis.set_major_formatter(ticker.FuncFormatter(lambda x, pos: f"{x:.0f}"))
else:
sum_hist = hist.sum()
if kind == "probability":
ax.yaxis.set_major_formatter(
ticker.FuncFormatter(lambda x, pos: f"{x/sum_hist:.2f}")
)
else:
ax.yaxis.set_major_formatter(
ticker.FuncFormatter(lambda x, pos: f"{x/sum_hist:.0%}")
)
fig, axs = plt.subplots(1, 2, figsize=(10, 3), sharey=True)
plot_letter_histogram(
grab_lowercase(histo_np), grab_lowercase(bin_edges), kind="count", ax=axs[0]
)
plot_letter_histogram(
grab_uppercase(histo_np), grab_uppercase(bin_edges), kind="count", ax=axs[1]
)
axs[0].set(title="Lowercase")
axs[1].set(title="Uppercase");
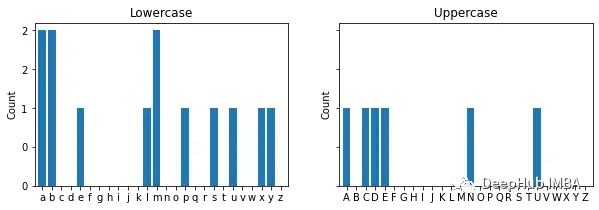
首先让我们编写CPU版本的函数来理解机制。
def histogram_cpu(arr):
histo = np.zeros(128, dtype=np.int64)
for char in arr:
if char < 128:
histo[char] += 1
return histo
histo_cpu = histogram_cpu(my_str_array)
assert (histo_cpu - histo_np).sum() == 0 # Matches numpy version
由于每个 ASCII 字符都映射到 128 元素数组中的一个 bin,因此我们需要做的就是找到它的 bin 并加 1,只要该 bin 在 0 和 127(包括)之间即可。
理解了我们的函数实现,下面我们来完成GPU版本:
# Example 4.3: A GPU histogram
@cuda.jit
def kernel_histogram(arr, histo):
i = cuda.grid(1)
threads_per_grid = cuda.gridsize(1)
for iarr in range(i, arr.size, threads_per_grid):
if arr[iarr] < 128:
cuda.atomic.add(histo, arr[iarr], 1)
@cuda.jit
def kernel_zero_init(arr):
i = cuda.grid(1)
threads_per_grid = cuda.gridsize(1)
for iarr in range(i, arr.size, threads_per_grid):
arr[iarr] = 0
threads_per_block = 128
blocks_per_grid = 32
my_str_array_gpu = cuda.to_device(my_str_array)
histo_gpu = cuda.device_array((128,), dtype=np.int64)
kernel_zero_init[1, 128](histo_gpu)
kernel_histogram[blocks_per_grid, threads_per_block](my_str_array_gpu, histo_gpu)
histo_cuda = histo_gpu.copy_to_host()
assert (histo_cuda - histo_cpu).sum() == 0
可以看到我们的函数可以正常工作了。这个内核非常简单并且与串行版本结构相同。它以标准的 1D 循环结构开始,使用原子加法。Numba 中的原子加法有三个参数:需要递增的数组 (histo)、需要加法操作的数组位置(arr[iarr]),需要相加的值(在本例中为 1)。
下面让我们看看在更大的数据集中如何使用
# Get the complete works of William Shakespeare
URL = "https://www.gutenberg.org/cache/epub/100/pg100.txt"
response = requests.get(URL)
str_bill = response.text
print(str_bill.split("\r")[0])
# •The Project Gutenberg eBook of The Complete Works of William Shakespeare, by William Shakespeare
str_bill_array = np.frombuffer(bytes(str_bill, "utf-8"), dtype=np.uint8)
str_bill_array.size
# 5757359
这里我们将处理大约570万个字符。让我们运行并记录目前为止的三个版本。
histo_bill_np, _ = np.histogram(str_bill_array, bins=128, range=(0, 128))
niter = 10
elapsed_np = 0.0
for i in trange(niter):
tic = perf_counter()
np.histogram(str_bill_array, bins=128, range=(0, 128))
toc = perf_counter()
elapsed_np += 1e3 * (toc - tic) # Convert to ms
elapsed_np /= niter
niter = 2 # very slow!
elapsed_cpu = 0.0
for i in trange(niter):
tic = perf_counter()
histogram_cpu(str_bill_array)
toc = perf_counter()
elapsed_cpu += 1e3 * (toc - tic) # in ms
elapsed_cpu /= niter
class CUDATimer:
def __init__(self, stream):
self.stream = stream
self.elapsed = None # in ms
def __enter__(self):
self.event_beg = cuda.event()
self.event_end = cuda.event()
self.event_beg.record(stream=self.stream)
return self
def __exit__(self, type, value, traceback):
self.event_end.record(stream=self.stream)
self.event_end.wait(stream=self.stream)
self.event_end.synchronize()
self.elapsed = self.event_beg.elapsed_time(self.event_end)
threads_per_block = 128
blocks_per_grid = 32 * 80
str_bill_array_gpu = cuda.to_device(str_bill_array)
histo_gpu = cuda.device_array((128,), dtype=np.int64)
stream = cuda.stream()
niter = 100
elapsed_gpu = 0.0
for i in trange(niter):
kernel_zero_init[1, 128, stream](histo_gpu)
with CUDATimer(stream=stream) as ct:
kernel_histogram[blocks_per_grid, threads_per_block, stream](
str_bill_array_gpu, histo_gpu
)
elapsed_gpu += ct.elapsed
elapsed_gpu /= niter
cuda.synchronize()
fig, ax = plt.subplots()
rects = ax.bar(
["NumPy", "Naive CPU", "GPU"],
[elapsed_np / elapsed_gpu, elapsed_cpu / elapsed_gpu, elapsed_gpu / elapsed_gpu],
)
ax.bar_label(rects, padding=0, fmt="%.0fx")
ax.set(title="Performance relative to GPU version", ylabel="Times slower")
ax.yaxis.set_major_formatter(ticker.StrMethodFormatter("{x:.0f}x"))
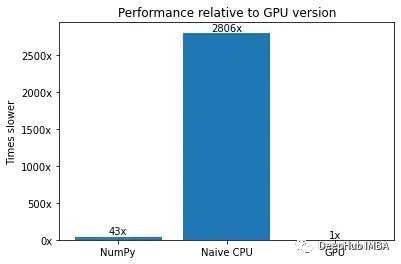
上图以GPU版本为基准,可以看到NumPy版本至少要慢40倍,而我们的CPU版本要慢数千倍。GPU可以在几毫秒内处理这570万个字符数据集,而CPU解决方案需要超过10秒。这意味着我们可以在几秒钟内处理200亿字符数据集(如果我们的GPU拥有超过20gb的RAM),而在最慢的CPU版本中这将需要一个多小时。
我们还能改进它吗?让我们重新查看这个内核的内存访问模式。
for iarr in range(i, arr.size, threads_per_grid):
if arr[iarr] < 128:
cuda.atomic.add(histo, arr[iarr], 1)
histo是位于GPU全局内存中的128元素数组。在任意一点启动的每个线程都试图访问该数组的某个元素(即元素arr[iarr])。因此在任何一个时间点上,我们有大约threads_per_block * blocks_per_grid = 128 × 32 × 80 = 327,680个线程试图访问128个元素。所以我们平均有32 × 80 = 2560个线程在竞争访问同一个全局内存地址。
为了提高速度,我们可以在共享内存数组中计算局部直方图
共享数组位于芯片上,因此读/写速度更快
共享数组对每个线程块都是本地的,访问的线程更少,竞争就少。
这里我们假设字符是均匀分布的。但是自然数据集中的字符分布可能不是均匀分布的。这点需要注意, 例如,自然语言文本中的大多数字符都是小写字母,我们这里暂时不考虑这种情况,还是以平均的2560个线程来计算。
# Example 4.4: A GPU histogram without as many memory conflicts
@cuda.jit
def kernel_histogram_shared(arr, histo):
# Create shared array to hold local histogram
histo_local = cuda.shared.array((128,), numba.int64)
histo_local[cuda.threadIdx.x] = 0 # initialize to zero
cuda.syncthreads() # ensure all threads in the same block "registered" the initialization
i = cuda.grid(1)
threads_per_grid = cuda.gridsize(1)
for iarr in range(i, arr.size, threads_per_grid):
if arr[iarr] < 128:
cuda.atomic.add(
histo_local, arr[iarr], 1
) # fewer threads competing for the same memory
# Ensure all threads in the block are up to date
cuda.syncthreads()
# Update global memory histogram with values from local histograms
cuda.atomic.add(histo, cuda.threadIdx.x, histo_local[cuda.threadIdx.x])
上一个计算中我们有2,560 个线程竞争访问同一内存地址,而现在我们有 2,560 ÷ 128 = 20 个线程。在内核函数的最后,我们需要对所有本地结果求和。由于有 32 × 80 = 2,560 个块,这意味着有 2,560 个线程尝试写入全局内存。所需需要确保每个线程只执行一次。
让我们看看这个新版本与以前的版本相比有没有提升!
str_bill_array_gpu = cuda.to_device(str_bill_array)
niter = 100
elapsed_gpu_shared = 0.0
for i in trange(niter):
kernel_zero_init[1, 128, stream](histo_gpu)
cuda.synchronize()
with CUDATimer(stream=stream) as ct:
kernel_histogram_shared[blocks_per_grid, threads_per_block, stream](
str_bill_array_gpu, histo_gpu
)
elapsed_gpu_shared += ct.elapsed
elapsed_gpu_shared /= niter
cuda.synchronize()
fig, ax = plt.subplots()
rects = ax.bar(
["NumPy", "Naive GPU", "GPU"],
[
elapsed_np / elapsed_gpu_shared,
elapsed_gpu / elapsed_gpu_shared,
elapsed_gpu_shared / elapsed_gpu_shared,
],
)
ax.bar_label(rects, padding=0, fmt="%.1fx")
ax.set(title="Performance relative to improved GPU version", ylabel="Times slower")
ax.yaxis.set_major_formatter(ticker.StrMethodFormatter("{x:.0f}x"))
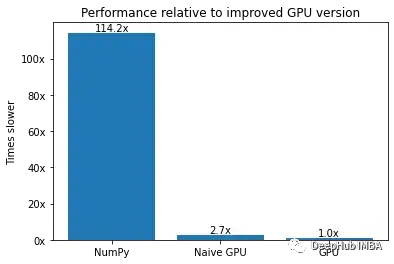
可以看到这比第一版本又提高了大约3倍!
我们将块的数量设置为32 × SMs数量的倍数,就像之前的教程中建议的那样。但几倍合适呢?我们来计算一下!
threads_per_block = 128
elapsed_conflict = []
elapsed_shared = []
block_range = range(10, 1000, 5)
histo_gpu = cuda.device_array((128,), np.int64, stream=stream)
for i in trange(block_range.start, block_range.stop, block_range.step):
blocks_per_grid = 32 * i
elapsed1 = 0.0
elapsed2 = 0.0
niter = 50
for i in range(niter):
kernel_zero_init[1, 128, stream](histo_gpu)
with CUDATimer(stream) as ct1:
kernel_histogram[blocks_per_grid, threads_per_block, stream](
str_bill_array_gpu, histo_gpu
)
elapsed1 += ct1.elapsed
kernel_zero_init[1, 128, stream](histo_gpu)
with CUDATimer(stream) as ct2:
kernel_histogram_shared[blocks_per_grid, threads_per_block, stream](
str_bill_array_gpu, histo_gpu
)
elapsed2 += ct2.elapsed
elapsed_conflict.append(elapsed1 / niter)
elapsed_shared.append(elapsed2 / niter)
fastest_sm_conflict = list(block_range)[np.argmin(elapsed_conflict)]
fastest_sm_shared = list(block_range)[np.argmin(elapsed_shared)]
fig, ax = plt.subplots()
ax.plot(block_range, elapsed_conflict, color="C0")
ax.axvline(fastest_sm_conflict, ls="--", color="C0")
ax.yaxis.label.set_color("C0")
ax.tick_params(axis="y", colors="C0")
ax.set(ylabel="Time of conflicted version [ms]")
ax2 = ax.twinx()
ax2.plot(block_range, elapsed_shared, color="C3")
ax2.axvline(fastest_sm_shared, ls="--", color="C3")
ax2.yaxis.label.set_color("C3")
ax2.tick_params(axis="y", colors="C3")
ax2.set(ylabel="Time of shared version [ms]");
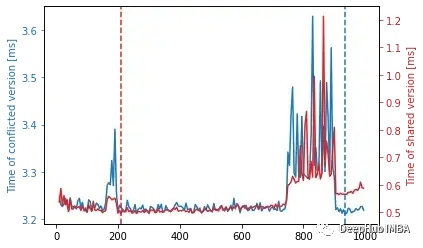
首先,我们需要两个轴来显示数据,因为naïve版本(蓝色)要慢得多。其次,竖线显示了对于某个函数,有多少SM是最优的。最后,尽管naïve版本不会随着添加更多块而变差,但共享版本却不是这样。为什么会这样?请记住共享数组版本包含两个部分
- 第一部分,少数线程竞争相同(快速)内存(共享数组部分)。
- 第二部分,许多线程竞争相同的(慢的)内存(最后的原子添加)。
随着添加更多的块,在naïve版本中它很快就会遇到瓶颈,而在共享数组版本中,竞争在第一部分保持不变,但在第二部分有所增加。而另一方面,太少的块不能产生足够的并行化(对于任何一个版本)。上图找到了这两个极端之间的“平衡点”。
使用互斥锁锁定资源
在前面的示例中,我们使用的是具有整数值的原子加法操作来锁定某些资源,并确保每次只有一个线程控制这些资源。加法并不是唯一的原子操作,它也只限制在整数值。Numba CUDA支持对整数和浮点数的各种原子操作。但是很久以前(CUDA compute 1.x),浮点数原子并不存在(需要注意)。因此如果我们需要另一种方式来实现浮点数的原子操作。
虽然现在原子操作确实支持浮点数,但这里介绍的“互斥”操作在某些情况下仍然有用。
互斥:mutex,是一种向试图访问它的线程发出某些资源可用或不可用信号的方式。可以使用采用两个值的变量创建互斥量:
0: 🟢 ,可以继续使用某个内存/资源
1: 🔴 ,不能使用/访问某个内存/资源
要锁定内存,应该将互斥锁设定为1,要解锁互斥锁应该设置为0。但是这里需要小心的是,如果一个线程(非原子地)写入互斥锁,而其他线程可能正在访问该资源,则会产生数据的混乱,甚至更糟造成死锁。另一个问题是互斥锁只有在之前没有被锁定的情况下才会被锁定。在写入1(用于锁定)之前,我需要读取互斥锁并确保它为0(未锁定)。CUDA提供了一个特殊的操作来原子地完成这两件事:atomicCAS。在Numba CUDA中,它的名字更明确:
cuda.atomic.compare_and_swap(array, old, val)
如果array [0] 的当前值等于旧值(这是“比较”部分),则此函数只会自动将 val 分配给array [0](这是“赋值”部分);否则它现在立刻赋值。并且它还会以原子方式返回 array[0] 的当前值。所以要锁定互斥锁,我们可以
cuda.atomic.compare_and_swap(mutex, 0, 1)
大师上面这行代码又有一个问题:如果线程读取了一个1(锁定),它就会继续执行,这很可能不是我们想要的。理想情况下,我们希望线程停止继续运行(等待),直到其他线程锁定结束。因此可以这样使用
while cuda.atomic.compare_and_swap(mutex, 0, 1) != 0:
pass
这样线程将持续等待,直到它能够正确地获得锁并锁定。while循环的意思就是,当前值1不同于0 (while条件)。它将一直在这个循环中,直到它最终能够读取当前值为0(其他线程的互斥锁已经解锁),这时它将1赋值给互斥锁。
如果要解锁,我们只需要给互斥锁原子地赋值一个0,例如:
cuda.atomic.exch(array, idx, val)
它只是原子赋值array[idx] = val,返回array[idx]的旧值(原子加载)。因为我们不会使用这个函数的返回值,所以可以把它看作一个原子赋值(例如,atomic_add(array, idx, val)是array[idx] += val,就像exch(array, idx, val)是array[idx] = val一样)。
我们介绍了锁定和解锁机制,让我们使用使用互斥锁实现原子“add”。
# Example 4.5: An atomic add with mutex.
@cuda.jit(device=True)
def lock(mutex):
while cuda.atomic.compare_and_swap(mutex, 0, 1) != 0:
pass
cuda.threadfence()
@cuda.jit(device=True)
def unlock(mutex):
cuda.threadfence()
cuda.atomic.exch(mutex, 0, 0)
@cuda.jit
def add_one_mutex(x, mutex):
lock(mutex) # Threads will stall here until they can atomically read 0 from
# the mutex, at which point they will atomically write a 1 to it
x[0] += 1 # Only a single thread will access this resource at a time, all
# others will be waiting in the line above
unlock(mutex) # The thread atomically writes a 0 to the mutex, releasing it
# all other threads are trying to obtain the lock
dev_val = cuda.to_device(np.zeros((1,)))
mutex = cuda.to_device(np.zeros((1,), dtype=np.int64))
add_one_mutex[10, 16](dev_val, mutex)
dev_val.copy_to_host()
# array([160.])
上面的代码相很直接:有一个内核,它锁定线程的执行,直到它们自己可以获得一个解锁的互斥锁。然后它将更新x[0]的值并解锁互斥锁。在任何情况下x[0]都不会被多个线程读或写,这实现了原子性!
上面的代码中只有一个细节没有涉及,那就是cuda.threadfence()的使用。本例中不需要这样做,但是要确保锁定和解锁机制的正确性。下面会看到原因!
互斥锁示例:点积操作
在本系列的第2部分中,我们学习了如何在GPU中应用简化。我们用它们来计算一个数组的和。我们的代码的一个不优雅的方面是,我们把一些求和的工作留给了CPU。我们当时缺乏的是应用原子操作的能力。
我们将使用本系列文章的第2部分的点积操作来进行互斥锁的示例,第2部分中,最后的一些求和工作是使用CPU来完成的,有了互斥锁,我们就不会返回“部分”点积,而是通过使用互斥锁在GPU中使用原子求和将所有的工作都是用GPU完成:
threads_per_block = 256
blocks_per_grid = 32 * 20
# Example 4.6: A partial dot product
@cuda.jit
def dot_partial(a, b, partial_c):
igrid = cuda.grid(1)
threads_per_grid = cuda.gridsize(1)
s_thread = 0.0
for iarr in range(igrid, a.size, threads_per_grid):
s_thread += a[iarr] * b[iarr]
s_block = cuda.shared.array((threads_per_block,), numba.float32)
tid = cuda.threadIdx.x
s_block[tid] = s_thread
cuda.syncthreads()
i = cuda.blockDim.x // 2
while i > 0:
if tid < i:
s_block[tid] += s_block[tid + i]
cuda.syncthreads()
i //= 2
# Above this line, the code will remain exactly the same in the next version
if tid == 0:
partial_c[cuda.blockIdx.x] = s_block[0]
# Example 4.6: A full dot product with mutex
@cuda.jit
def dot_mutex(mutex, a, b, c):
igrid = cuda.grid(1)
threads_per_grid = cuda.gridsize(1)
s_thread = 0.0
for iarr in range(igrid, a.size, threads_per_grid):
s_thread += a[iarr] * b[iarr]
s_block = cuda.shared.array((threads_per_block,), numba.float32)
tid = cuda.threadIdx.x
s_block[tid] = s_thread
cuda.syncthreads()
i = cuda.blockDim.x // 2
while i > 0:
if tid < i:
s_block[tid] += s_block[tid + 1]
cuda.syncthreads()
i //= 2
# Instead of assigning the partial reduction to a global memory array, we
# will atomically add it to c[0].
if tid == 0:
lock(mutex)
c[0] += s_block[0]
unlock(mutex)
N = 10_000_000
a = np.ones(N, dtype=np.float32)
b = (np.ones(N) / N).astype(np.float32)
dev_a = cuda.to_device(a)
dev_b = cuda.to_device(b)
dev_c = cuda.device_array((1,), dtype=a.dtype)
dev_partial_c = cuda.device_array((blocks_per_grid,), dtype=a.dtype)
dev_mutex = cuda.device_array((1,), dtype=np.int32)
dot_partial[blocks_per_grid, threads_per_block](dev_a, dev_b, dev_partial_c)
dev_partial_c.copy_to_host().sum()
# 0.9999999
kernel_zero_init[1, 1](dev_c)
dot_mutex[blocks_per_grid, threads_per_block](dev_mutex, dev_a, dev_b, dev_c)
dev_c.copy_to_host().item()
# 1.0000089406967163
以上代码可以说是我们这系列文章4部分的总结。
在我们结束之前,需要重点说一下cuda.threadfence。来自CUDA的“bible”(B.5)。__threadfence函数是memory fence函数,用来保证线程间数据通信的可靠性。与同步函数不同,memory fence不能保证所有线程运行到同一位置,只保证执行memory fence函数的线程生产的数据能够安全地被其他线程消费。一个线程调用__threadfence后,该线程在该语句前对全局存储器或共享存储器的访问已经全部完成,执行结果对grid中的所有线程可见。
如果在解锁互斥锁之前省略了线程保护,即使在使用原子操作时也可能读取过时的信息,因为内存可能还没有被其他线程写入。所以在解锁之前,必须确保更新了内存引用。这个问题是 Alglave 等人首次提出的。在2015 年修复程序被 CUDA by Examples 勘误表中收录。
总结
本文介绍了原子操作,这是协调线程的基本要素。还有互斥锁模式,它利用原子来创建自定义区域,一次只能有一个线程访问这些区域。
本文代码在这里:
https://colab.research.google.com/drive/1Eq1Xyuq8hJ440ma_9OBrEVdGm3bIyigt?usp=sharing
在本系列的篇文章中,介绍了在各种常见情况下使用 Numba CUDA。这些教程并不详尽,但是目的是介绍CUDA 的一些基础的知识,让你对CUDA有一个大概的印象。
最后,这里我们没有涉及的一些主题:动态并行性(让内核启动内核)、复杂的同步(例如,warp-level、协作组)、复杂的内存保护(我们在上面提到过)、多 GPU、纹理和许多其他主题。因为Numba CUDA(从 0.56 版)目前不支持其中一些技术,并且一些技术对于介绍教程而言太高级了。
在 Python 生态系统中,除了 Numba 之外,还有许多可以 GPU 的解决方案。而且它们大多可以进行互操作,因此不必只选择一个。PyCUDA、CUDA Python、RAPIDS、PyOptix、CuPy 和 PyTorch 都是可以进行学习的。
作者:Carlos Costa, Ph.D.