临界点
优化时参数不断更新而损失降不下去的原因猜想:梯度为零
梯度为零的情况:局部极值和鞍点
把梯度为零的点统称为临界点
逃离鞍点可能让损失更低
判断种类
给定
θ
′
,
θ
′
附近的
L
(
θ
)
可近似为:
\theta',\theta'附近的L(\theta)可近似为:
θ′,θ′附近的L(θ)可近似为:
L
(
θ
)
≈
L
(
θ
′
)
+
(
θ
−
θ
′
)
T
g
+
1
2
(
θ
−
θ
′
)
T
H
(
θ
−
θ
′
)
L(\theta) \approx L(\theta') + (\theta - \theta')^Tg + \dfrac{1}{2}(\theta - \theta')^TH(\theta - \theta')
L(θ)≈L(θ′)+(θ−θ′)Tg+21(θ−θ′)TH(θ−θ′)(泰勒级数近似)
在临界点g为零,得:
L
(
θ
)
≈
L
(
θ
′
)
+
1
2
(
θ
−
θ
′
)
T
H
(
θ
−
θ
′
)
L(\theta) \approx L(\theta') + \dfrac{1}{2}(\theta - \theta')^TH(\theta - \theta')
L(θ)≈L(θ′)+21(θ−θ′)TH(θ−θ′)
令
v
=
θ
−
θ
′
v = \theta - \theta'
v=θ−θ′
当
∀
v
,
v
T
H
v
>
0
,
则
θ
′
为局部极小值点
;
<
0
,
则
θ
′
为局部极大值点
;
有时大于零,有时小于零,则
θ
′
为鞍点
\forall v,v^THv > 0,则\theta'为局部极小值点; < 0,则\theta'为局部极大值点; 有时大于零,有时小于零,则\theta'为鞍点
∀v,vTHv>0,则θ′为局部极小值点;<0,则θ′为局部极大值点;有时大于零,有时小于零,则θ′为鞍点
改进判断方法:算出海森矩阵H后,只看H的特征值
若H的所有特征值为正,H为;正定矩阵,则
v
T
H
v
>
0
v^THv > 0
vTHv>0,以此类推
逃离鞍点
设
λ
为
H
的一个特征值,
u
为其对应的特征向量,令
u
=
θ
−
θ
′
,则有
v
T
H
v
=
λ
∥
u
∥
2
\lambda 为H的一个特征值,u为其对应的特征向量,令 u = \theta - \theta',则有v^THv = \lambda \lVert u\rVert^2
λ为H的一个特征值,u为其对应的特征向量,令u=θ−θ′,则有vTHv=λ∥u∥2
若
λ
<
0
\lambda < 0
λ<0,只要
θ
=
θ
′
+
u
\theta = \theta' + u
θ=θ′+u,则说明沿着**u**的方向更新
θ
′
\theta'
θ′,损失会变小
缺点:运算量过大
高维观点:低纬度空间中的局部极小值点,在更高维的空间中可能是鞍点
启示:局部极小值并不常见,训练到梯度很小的时候参数不再更新往往是遇到了鞍点
批量
把所有的数据分成一个一个批量,每个大小为B。每次更新参数时,取出B笔数据用来计算出损失和梯度更新参数。遍历所有批量的过程称为一个回合。在把数据分为批量的时候会进行随机打乱,如每个回合的批量的数据都不一样

批量大小对梯度下降法的影响
优点缺点批量梯度下降法每次更新更稳定、更准确每次迭代的计算量大随机梯度下降法每次更新计算量小每次迭代算出来的损失相对带有更多噪声
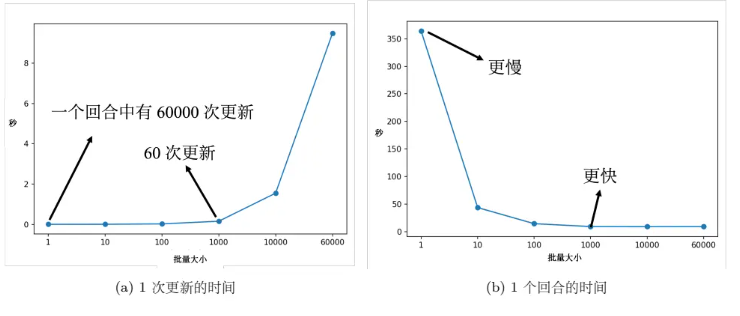
- 实际上,考虑并行运算,批量梯度下降花费的时间不一定更长;对于比较大的批量,计算损失和梯度花费的时间不一定比使用小批量的计算时间长 。当然 GPU 并行计算的能力还是存在极限的,当批量大小很大的时候,时间还是会增加的。 当批量大小非常大的时候,GPU 在“跑”完一个批量,计算出梯度所花费的时间还是会随着批量大小的增加而逐渐增长。
实际上当批量大小小的时候,要“跑”完一个回合,花的时间是比大的。假设训练数据只有 60000 笔,批量大小设 1,要 60000 个更新才能“跑”完一个回合;如果批量大小等于 1000,60 个更新才能“跑”完一个回合,计算梯度的时间差不多。但60000 次更新跟 60 次更新比起来,其时间的差距量就非常大了。在有考虑并行计算的时候,大的批量大小反而是较有效率的,一个回合大的批量花的时间反而是比较少的。
- 随机梯度下降的梯度上引入了随机噪声,因此在非凸优化问题中,其相比批量梯度下降更容易逃离局部最小值。这不是过拟合,因为批量大小越大,训练准确率也是越低。因为用的是同一个模型,所以这不是模型偏见的问题。 但大的批量大小往往在训练的时候,结果比较差。这个是优化的问题,大的批量大小优化可能会有问题,小的批量大小优化的结果反而是比较好的。
可能的解释是批量梯度下降在更新参数的时候,沿着一个损失函数来更新参数,走到一个局部最小值或鞍点显然就停下来了。梯度是零,如果不看海森矩阵,梯度下降就无法再更新参数了 。但小批量梯度下降法每次是挑一个批量计算损失,所以每一次更新参数的时候所使用的损失函数是有差异的。选到第一个批量的时候,用 L1 计算梯度;选到第二个批量的时候,用 L2 计算梯度。假设用 L1 算梯度的时候,梯度是零,就会卡住。但 L2 的函数跟 L1 又不一样,L2 不一定会卡住,可以换下个批量的损失 L2 计算梯度,模型还是可以训练,还是有办法让损失变小,所以这种有噪声的更新方式反而对训练其实是有帮助的。
- 局部最小值有好最小值跟坏最小值之分,如果局部最小值在一个“峡谷”里面,它是坏的最小值;如果局部最小值在一个平原上,它是好的最小值。训练的损失跟测试的损失函数是不一样的,这有两种可能。一种可能是本来训练跟测试的分布就不一样;另一种可能是因为训练跟测试都是从采样的数据算出来的,训练跟测试采样到的数据可能不一样,所以它们计算出的损失是有一点差距。 对在一个“盆地”里面的最小值,其在训练跟测试上面的结果不会差太多,只差了一点点。但对在右边在“峡谷”里面的最小值,一差就可以天差地远 。虽然它在训练集上的损失很低,但训练跟测试之间的损失函数不一样,因此测试时,损失函数一变,计算出的损失就变得很大。
大的批量大小会让我们倾向于走到“峡谷”里面,而小的批量大小倾向于让我们走到“盆地”里面。小的批量有很多的损失,其更新方向比较随机,其每次更新的方向都不太一样。即使“峡谷”非常窄,它也可以跳出去,之后如果有一个非常宽的“盆地”,它才会停下来。
动量
参照现实中物体的惯性,引入动量,每次在移动参数的时候,不是只往梯度的反方向来移动参数,而是根据梯度的反方向加上前一步移动的方向决定移动方向,用于对抗鞍点或局部最小值

版权归原作者 2301_79766496 所有, 如有侵权,请联系我们删除。