机器学习分类算法之朴素贝叶斯

朴素贝叶斯

背景介绍

20世纪80年代发展起来，最早由Judea Pearl于1986年提出，多用于专家系统，是处理不确定性

知识和推理问题的最流行的方法。

贝叶斯算法基于贝叶斯统计分析的数学原理，是概率论和图论相结合的产物。

朴素贝叶斯模型的泛化能力要比线性分类器（如LogisticRegression 和 LinearSVC）稍差。

朴素贝叶斯模型如此高效的原因在于，它通过单独查看每个特征来学习参数，并从每个特征中收集简单的类别统计数据。

scikit-learn 中实现了三种朴素贝叶斯分类器：GaussianNB、 BernoulliNB 和** MultinomialNB**。 GaussianNB 可 应 用 于 任 意 连 续 数 据， 而BernoulliNB 假定输入数据为二分类数据， MultinomialNB 假定输入数据为计数数据（即每个特征代表某个对象的整数计数，比如一个单词在句子里出现的次数）。 BernoulliNB 和MultinomialNB 主要用于文本数据分类。

概念及原理

**频率 ****& **概率

频率：是指事件发生的频繁程度。严格定义是：在相同的条件下，进行n次试验，事件A发生的次数a称为事件A的频数，比值a/n 称为事件A发生的频率。

概率：是指某事件出现的可能性大小。严格定义是：设E是随机试验（一定是要随机的），S是样本空间（说白了就是可能出现的每种情况），对于E的每一个事件A赋予一个实数，记作P(A)，称为事件A的概率，如果集合函数P（·）满足以下条件：

1.非负性：P(A)≥0；
2.规范性：对必然事件S，有P(S)=1
3.可列可加性：对于两两互不相容事件，或事件的概率=各单独事件的概率之和

**先验概率 ****& ****后验概率 ****& **条件概率

先验概率：事件发生前的预判概率。可以是基于历史数据的统计，可以由背景常识得出，也可以是人的主观观点给出。一般都是单独事件概率，如P(x),P(y)。
条件概率：一个事件发生后另一个事件发生的概率。一般的形式为P(x|y)表示y发生的条件下x发生的概率。
后验概率：结果发生后反推事件发生原因的概率；或者说，基于先验概率求得的反向条件概率。概率形式与条件概率相同。

感觉又回到了大学里面的概率论与数理统计的课程，其实基本的思想就是如此

贝叶斯公式

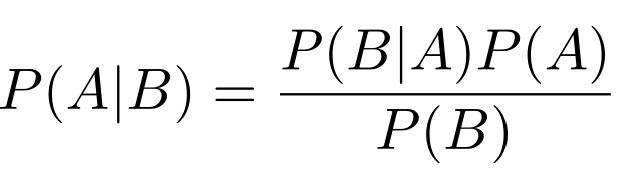
P（A|B）表示在B发生的条件下A发生的概率是多少？

全概率公式

贝叶斯公式的意义

案例：

某地区居民肝癌的发病率为0.0004，现用甲胎蛋白法进行普查。医学研究表明，化验结果是有错检的可能性。已知患有肝癌的人其化验结果99%呈阳性（有病），而没患肝癌的人其化验结果99.9%呈阴性（无病）。

现某人的检查结果呈阳性，问他真正得肝癌的概率有多大？

解答：

设A=“结果检查呈阳性”,B=“被检查患者确实有肝癌”，已知P(B)=0.0004, P(B-)=0.9996 , P(A|B)=0.99,P(A|B-)=0.001.由贝叶斯公式可得到：

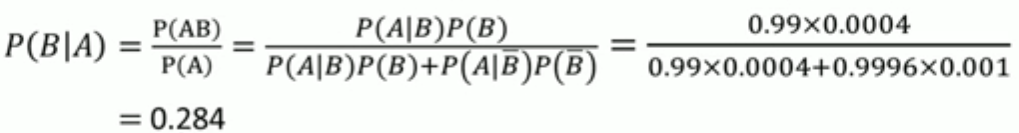
复检能够大大提高化验的准确率

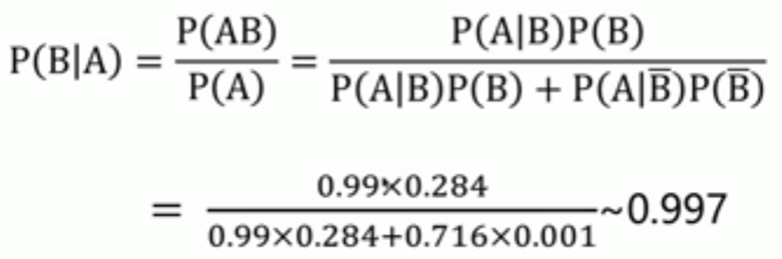
如果某人首次化验，成果呈阳性。第二次复检，仍然呈阳性。请问该患者患肝癌的概率有多大？
首次检查呈阳性的患者，他的P(B)=0.284，复检仍然呈阳性，则患肝癌的概率为：

贝叶斯算法

朴素贝叶斯（ Naive Bayes）模型是一种基于概率的学习方法

“朴素”不是指艰苦朴素的“朴素”，是指假设每个属性条件都是相互独立的，没有相关性

经典案例

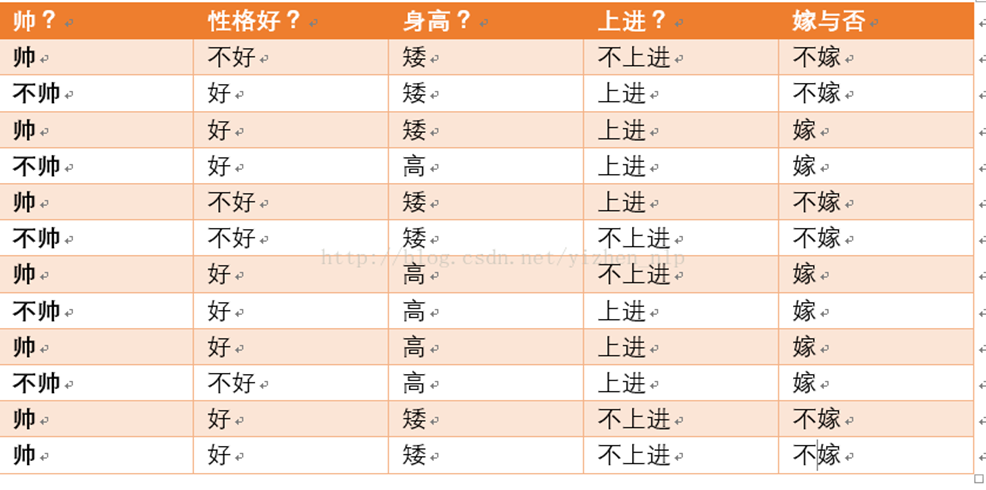
现在给我们的问题是，如果一对男女朋友，男生想女生求婚，男生的四个特点分别是不帅，性格不好，身高矮，不上进，请你判断一下女生是嫁还是不嫁？

看到上述规则的男同胞们，及时你被上帝关上了一扇窗，那你也可以自己撬开一扇门

朴素贝叶斯案例
这是一个典型的分类问题
数学问题就是比较

p(嫁|(不帅、性格不好、身高矮、不上进))

p(不嫁|(不帅、性格不好、身高矮、不上进))

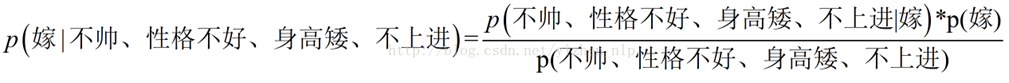
下面我将一个一个的进行统计计算（在数据量很大的时候，中心极限定理，频率是等于概率的）
p(嫁)=？
首先我们整理训练数据中，嫁的样本数如下：则 p(嫁) = 6/12（总样本数） = 1/2

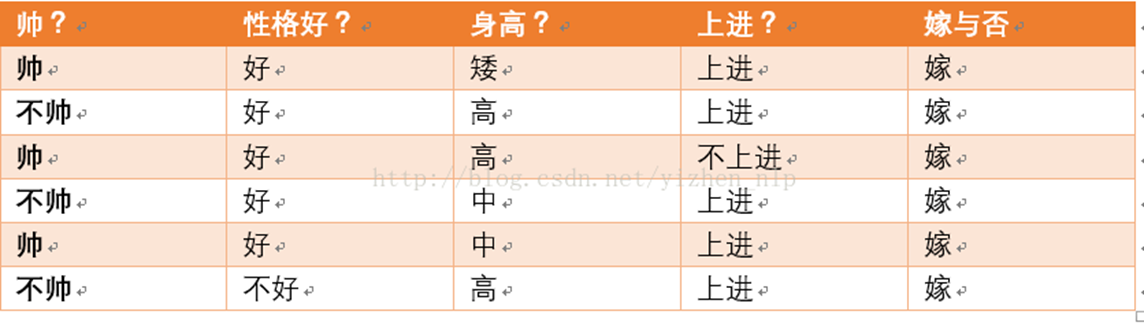
则 p(嫁) = 6/12（总样本数） = 1/2

p(不帅|嫁)=？统计满足样本数如下

则p(不帅|嫁) = 3/6 = 1/2 在嫁的条件下，看不帅有多少

带入其他统计量

= (1/21/61/61/61/2)/(5/121/37/12*5/12)

贝叶斯分类器

分母对于所有类别为常数，我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

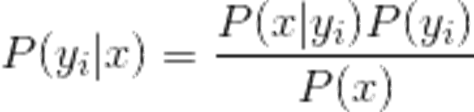
1、设x={a1,a2,a3,......am}为一个待分类项，而每个a为x的一个特征属性。
2、有类别集合C={y1,y2,......yn}。
3、计算P(y1|x),P(y2|x),......,P(yn|x),。
4、如果，P(yk|x)=max{P(y1|x),P(y2|x),......,P(yn|x)},则x属于yk。

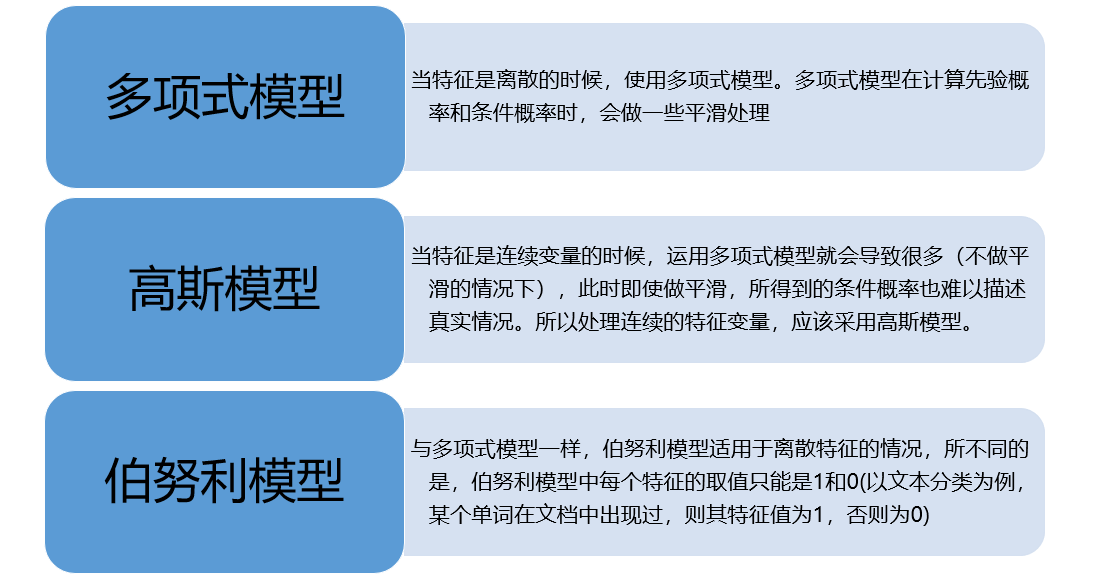
常见的三种贝叶斯模型

朴素贝叶斯应用场景

在文本分类中，假设我们有一个文档d∈X，X是文档向量空间(document space)，和一个固定的类集合C={c1,c2,…,cj}，类别又称为标签。

显然，文档向量空间是一个高维度空间。我们把一堆打了标签的文档集合<d,c>作为训练样本，<d,c>∈X×C。例如：<d,c>={Beijing joins the World Trade Organization, China}

对于这个只有一句话的文档，我们把它归类到 China，即打上china标签。我们期望用某种训练算法，训练出一个函数γ，能够将文档映射到某一个类别：γ:X→C

多项式贝叶斯

在多项式模型中， 设某文档d=(t1,t2,…,tk)，tk是该文档中出现过的单词，允许重复，则

先验概率P(c)= 类c下单词总数/整个训练样本的单词总数

类条件概率P(tk|c)=(类c下单词tk在各个文档中出现过的次数之和+1)/(类c下单词总数+|V|)

V是训练样本的单词表（即抽取单词，单词出现多次，只算一个），|V|则表示训练样本包含多少种单词。在这里，m=|V|, p=1/|V|。

P(tk|c)可以看作是单词tk在证明d属于类c上提供了多大的证据，而P(c)则可以认为是类别c在整体上占多大比例(有多大可能性)。

伯努利模型

伯努利模型跟多项式模型的差别在计算公式不同：

P(c)= 类c下文件总数/整个训练样本的文件总数

P(tk|c)=(类c下包含单词tk的文件数+1)/(类c的文档总数+2)

二者的计算粒度不一样，多项式模型以单词为粒度，伯努利模型以文件为粒度，因此二者的先验概率和类条件概率的计算方法都不同。

计算后验概率时，对于一个文档d，多项式模型中，只有在d中出现过的单词，才会参与后验概率计算，伯努利模型中，没有在d中出现，但是在全局单词表中出现的单词，也会参与计算，不过是作为“反方”参与的。

高斯模型

有些特征可能是连续型变量，比如说人的身高，物体的长度，这些特征如果使用决策树那些模型，可以转换成离散型的值，比如如果身高在160cm以下，特征值为1；在160cm和170cm之间，特征值为2；在170cm之上，特征值为3。也可以这样转换，将身高转换为3个特征，分别是f1、f2、f3，如果身高是160cm以下，这三个特征的值分别是1、0、0，若身高在170cm之上，这三个特征的值分别是0、0、1。

不过这些方式都不够细腻，高斯模型可以解决这个问题。高斯模型假设这些一个特征的所有属于某个类别的观测值符合高斯分布：

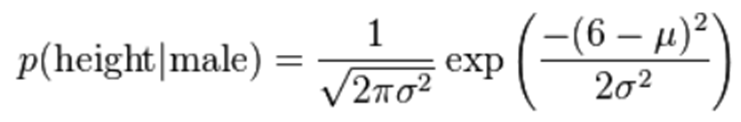
μ：获取各个类标记在各个特征上的均值

σ：获取各个类标记在各个特征上的方差

代码实现

高斯贝叶斯

# 加载模型
model = GaussianNB()
# 训练模型
model.fit(X_train,y_train)
# 预测值
y_pred = model.predict(X_test)

'''
评估指标
'''
# 求出预测和真实一样的数目
true = np.sum(y_pred == y_test )
print('预测对的结果数目为：', true)
print('预测错的的结果数目为：', y_test.shape[0]-true)
# 评估指标
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_score
print('预测数据的准确率为： {:.4}%'.format(accuracy_score(y_test,y_pred)*100))
print('预测数据的精确率为：{:.4}%'.format(
      precision_score(y_test,y_pred)*100))
print('预测数据的召回率为：{:.4}%'.format(
      recall_score(y_test,y_pred)*100))
# print("训练数据的F1值为：", f1score_train)
print('预测数据的F1值为：',
      f1_score(y_test,y_pred))
print('预测数据的Cohen’s Kappa系数为：',
      cohen_kappa_score(y_test,y_pred))
# 打印分类报告
from sklearn.metrics import classification_report
print('预测数据的分类报告为：','\n',
      classification_report(y_test,y_pred))

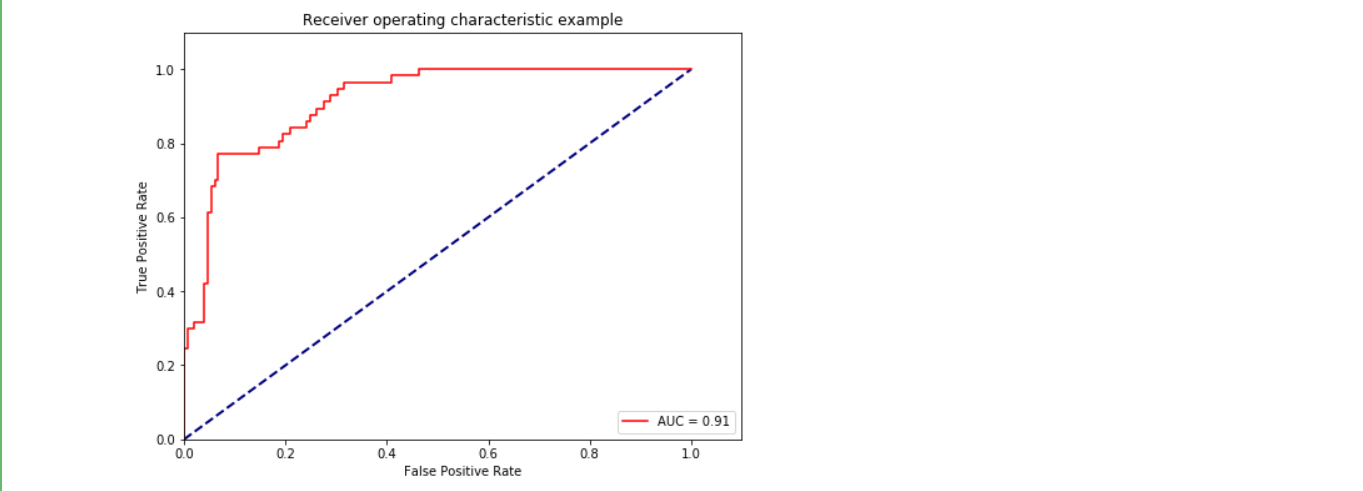
ROC曲线和AUC面积

from sklearn.metrics import precision_recall_curve
from sklearn import metrics
# 预测正例的概率
y_pred_prob=model.predict_proba(X_test)[:,1]
# y_pred_prob ,返回两列，第一列代表类别0,第二列代表类别1的概率
#https://blog.csdn.net/dream6104/article/details/89218239
fpr, tpr, thresholds = metrics.roc_curve(y_test,y_pred_prob, pos_label=2)
#pos_label，代表真阳性标签，就是说是分类里面的好的标签，这个要看你的特征目标标签是0,1，还是1,2
roc_auc = metrics.auc(fpr, tpr)  #auc为Roc曲线下的面积
# print(roc_auc)
plt.figure(figsize=(8,6))
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.plot(fpr, tpr, 'r',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
# plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0, 1.1])
plt.ylim([0, 1.1])
plt.xlabel('False Positive Rate') #横坐标是fpr
plt.ylabel('True Positive Rate')  #纵坐标是tpr
plt.title('Receiver operating characteristic example')
plt.show()

对于高斯贝叶斯模型的参数，一般是不需要进行调参的，使用该模型一般在数据集以及特征方面进行改进

通过模型进行选择重要的特征：9个，用于预测

from sklearn.model_selection import train_test_split,cross_val_score #拆分训练集和测试集
import lightgbm as lgbm #轻量级的高效梯度提升树
X_name=df.corr()[["n23"]].sort_values(by="n23",ascending=False).iloc[1:].index.values.astype("U")
X=df.loc[:,X_name.tolist()]
y=df.loc[:,['n23']]
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,stratify=y,random_state=1)
lgbm_reg = lgbm.LGBMRegressor(objective='regression',max_depth=6,num_leaves=25,learning_rate=0.005,n_estimators=1000,min_child_samples=80, subsample=0.8,colsample_bytree=1,reg_alpha=0,reg_lambda=0)
lgbm_reg.fit(X_train, y_train)
#选择最重要的20个特征，绘制他们的重要性排序图
lgbm.plot_importance(lgbm_reg, max_num_features=9)
 
##也可以不使用自带的plot_importance函数，手动获取特征重要性和特征名，然后绘图
feature_weight = lgbm_reg.feature_importances_
feature_name = lgbm_reg.feature_name_
feature_sort = pd.Series(data = feature_weight ,index = feature_name)
feature_sort = feature_sort.sort_values(ascending = False)
# plt.figure(figsize=(10,8))
# sns.barplot(feature_sort.values,feature_sort.index, orient='h')
lgbm_name=feature_sort.index[:9].tolist()
lgbm_name

X=df.loc[:,lgbm_name]
y=df.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,stratify=y,random_state=1)

# 加载模型
model = GaussianNB()

# 训练模型
model.fit(X_train,y_train)
# 预测值
y_pred = model.predict(X_test)

'''
评估指标
'''
# 求出预测和真实一样的数目
true = np.sum(y_pred == y_test )
print('预测对的结果数目为：', true)
print('预测错的的结果数目为：', y_test.shape[0]-true)
# 评估指标
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_score
print('预测数据的准确率为： {:.4}%'.format(accuracy_score(y_test,y_pred)*100))
print('预测数据的精确率为：{:.4}%'.format(
      precision_score(y_test,y_pred)*100))
print('预测数据的召回率为：{:.4}%'.format(
      recall_score(y_test,y_pred)*100))
# print("训练数据的F1值为：", f1score_train)
print('预测数据的F1值为：',
      f1_score(y_test,y_pred))
print('预测数据的Cohen’s Kappa系数为：',
      cohen_kappa_score(y_test,y_pred))
# 打印分类报告
from sklearn.metrics import classification_report
print('预测数据的分类报告为：','\n',
      classification_report(y_test,y_pred))

from sklearn.metrics import precision_recall_curve
from sklearn import metrics
# 预测正例的概率
y_pred_prob=model.predict_proba(X_test)[:,1]
# y_pred_prob ,返回两列，第一列代表类别0,第二列代表类别1的概率
#https://blog.csdn.net/dream6104/article/details/89218239
fpr, tpr, thresholds = metrics.roc_curve(y_test,y_pred_prob, pos_label=2)
#pos_label，代表真阳性标签，就是说是分类里面的好的标签，这个要看你的特征目标标签是0,1，还是1,2
roc_auc = metrics.auc(fpr, tpr)  #auc为Roc曲线下的面积
# print(roc_auc)
plt.figure(figsize=(8,6))
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.plot(fpr, tpr, 'r',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
# plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0, 1.1])
plt.ylim([0, 1.1])
plt.xlabel('False Positive Rate') #横坐标是fpr
plt.ylabel('True Positive Rate')  #纵坐标是tpr
plt.title('Receiver operating characteristic example')
plt.show()

结果展示：

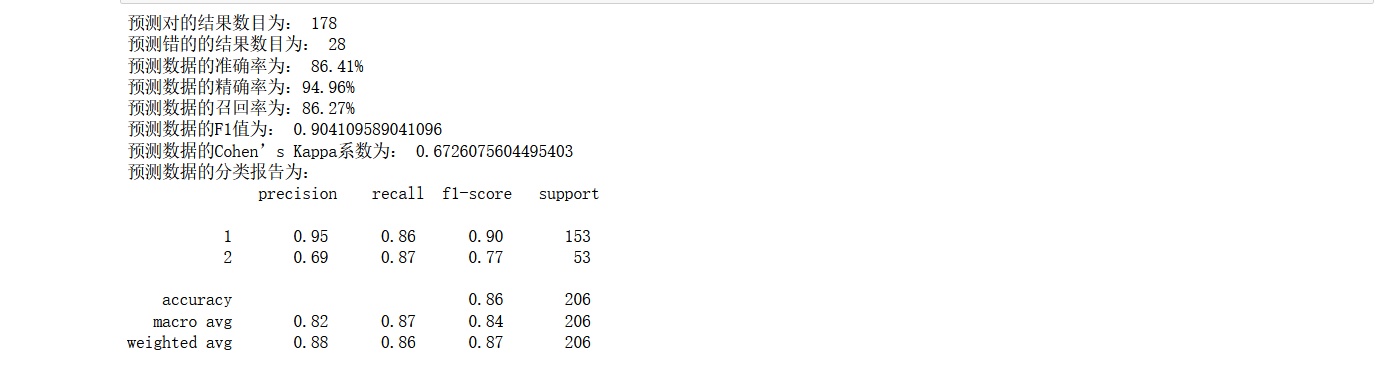
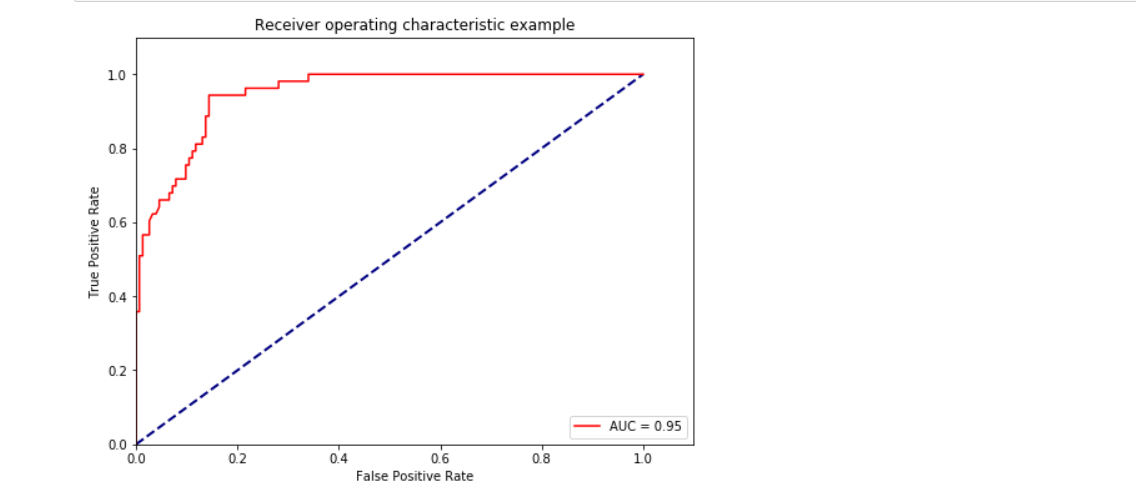
果不其然，通过了特征选取的方式，模型的效果有了一定的改善，这里你也可以结合之前的博客文章：

机器学习框架及评估指标详解

特征选取之单变量统计、基于模型选择、迭代选择

将所有的指标都可以进行探究最后通过特征选取等方法，去增加模型的指标

其他模型尝试

多项式贝叶斯

适用于服从多项分布的特征数据

class sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)

**

alpha

:先验平滑因子，默认等于1，当等于1时表示拉普拉斯平滑。

fit_prior

:是否去学习类的先验概率，默认是True

class_prior

:各个类别的先验概率，如果没有指定，则模型会根据数据自动学习， 每个类别的先验概率相同，等于类标记总个数N分之一。**

class_log_prior_:每个类别平滑后的先验概率
intercept_:是朴素贝叶斯对应的线性模型，其值和class_log_prior_相同
feature_log_prob_:给定特征类别的对数概率(条件概率)。 特征的条件概率=（指定类下指定特征出现的次数+alpha）/（指定类下所有特征出现次数之和+类的可能取值个数*alpha）
coef_: 是朴素贝叶斯对应的线性模型，其值和feature_log_prob相同
class_count_: 训练样本中各类别对应的样本数
feature_count_: 每个类别中各个特征出现的次数

伯努利朴素贝叶斯

用于多重伯努利分布的数据，即有多个特征，但每个特征都假设是一个二元 (Bernoulli, boolean) 变量

class sklearn.naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)

alpha:平滑因子，与多项式中的alpha一致。
binarize:样本特征二值化的阈值，默认是0。如果不输入，则模型会认为所有特征都已经是二值化形式了；如果输入具体的值，则模型会把大于该值的部分归为一类，小于的归为另一类。
fit_prior:是否去学习类的先验概率，默认是True
class_prior:各个类别的先验概率，如果没有指定，则模型会根据数据自动学习， 每个类别的先验概率相同，等于类标记总个数N分之一。

class_log_prior_

:每个类别平滑后的先验对数概率。

feature_log_prob_

:给定特征类别的经验对数概率。

class_count_

:拟合过程中每个样本的数量。

feature_count_

:拟合过程中每个特征的数量。

这些都是可以通过尝试进行探索，总的来说，纸上得来终觉浅，绝知此事要躬行。

优点缺点、参数总结

**MultinomialNB 和 BernoulliNB 都只有一个参数 alpha，用于控制模型复杂度。 **

alpha 的工作原理是，算法向数据中添加 alpha 这么多的虚拟数据点，这些点对所有特征都取正值。这可以将统计数据“平滑化”（smoothing）。 alpha 越大，平滑化越强，模型复杂度就越低。

算法性能对 alpha 值的鲁棒性相对较好，也就是说， alpha 值对模型性能并不重要。但调整这个参数通常都会使精度略有提高。
GaussianNB 主要用于高维数据，而另外两种朴素贝叶斯模型则广泛用于稀疏计数数据，比
如文本。

MultinomialNB 的性能通常要优于 BernoulliNB，特别是在包含很多非零特征的数据集（即大型文档）上。朴素贝叶斯模型的许多优点和缺点都与线性模型相同。它的训练和预测速度都很快，训练
过程也很容易理解。

该模型对高维稀疏数据的效果很好，对参数的鲁棒性也相对较好。朴素贝叶斯模型是很好的基准模型，常用于非常大的数据集，在这些数据集上即使训练线性模型可能也要花费大量时间。

每文一语

坚持也是一种快乐！