《一文搞懂IoU发展历程》GIoU、DIoU、CIoU、EIoU、αIoU、SIoU

《一文搞懂IoU发展历程》GIoU、DIoU、CIoU、EIoU、αIoU、SIoU

文章目录

IoU出现背景

目标检测任务的损失函数一般由

Classificition Loss

（分类损失函数）和

Bounding Box Regeression Loss

（回归损失函数）两部分构成。因此，更好的定位有利于模型精度的提高。在

IoU Loss

提出来之前，检测上有关候选框的回归主要是通过坐标的回归损失来优化。但

L1 Loss

和

L2 Loss

存在比较大的问题：

1. L1 Loss的问题：损失函数对x的导数为常数，在训练后期，x很小时，如果learning rate 不变，损失函数会在稳定值附近波动，很难收敛到更高的精度。
2. L2 Loss的问题：损失函数对x的导数在x值很大时，其导数也非常大，在训练初期不稳定。

而且，基于

L1/L2 Loss

的坐标回归不具有尺度不变性，且并没有将四个坐标之间的相关性考虑进去。因此，像

L1/L2 Loss

直接的坐标回归实际上很难描述两框之间的相对位置关系。

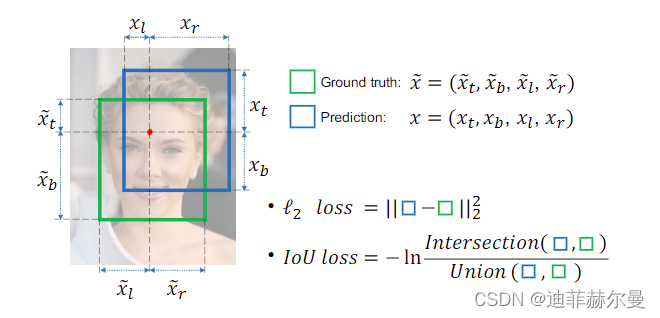
因此，在ACM2016的论文中提出了

IoU loss

，它将四个坐标点看成一个整体进行计算，具有尺度不变性（也就是对尺度不敏感）。

IoU Loss

的定义是先求出预测框和真实框之间的交集和并集之比，再求负对数，但是在实际使用中我们常常将

IoU Loss

写成

1-IoU

。如果两个框重合则交并比等于

1

，

Loss

为0说明重合度非常高。因此，

IoU

的取值范围为

[0,1]

。

什么是IoU？

IOU

的全称为交并比（Intersection over Union），是目标检测中使用的一个概念，

IoU

计算的是“预测的边框”和“真实的边框”的交叠率，即它们的交集和并集的比值。最理想情况是完全重叠，即比值为1。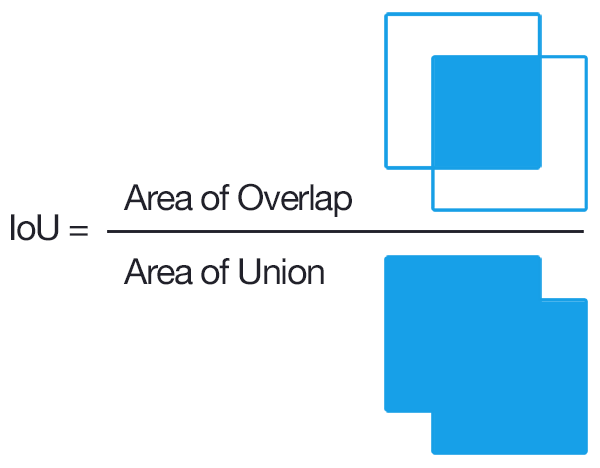

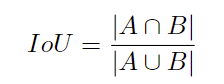
IoU发展历程

虽然

IoU Loss

虽然解决了

Smooth L1

系列变量相互独立和不具有尺度不变性的两大问题，但是它也存在两个问题：

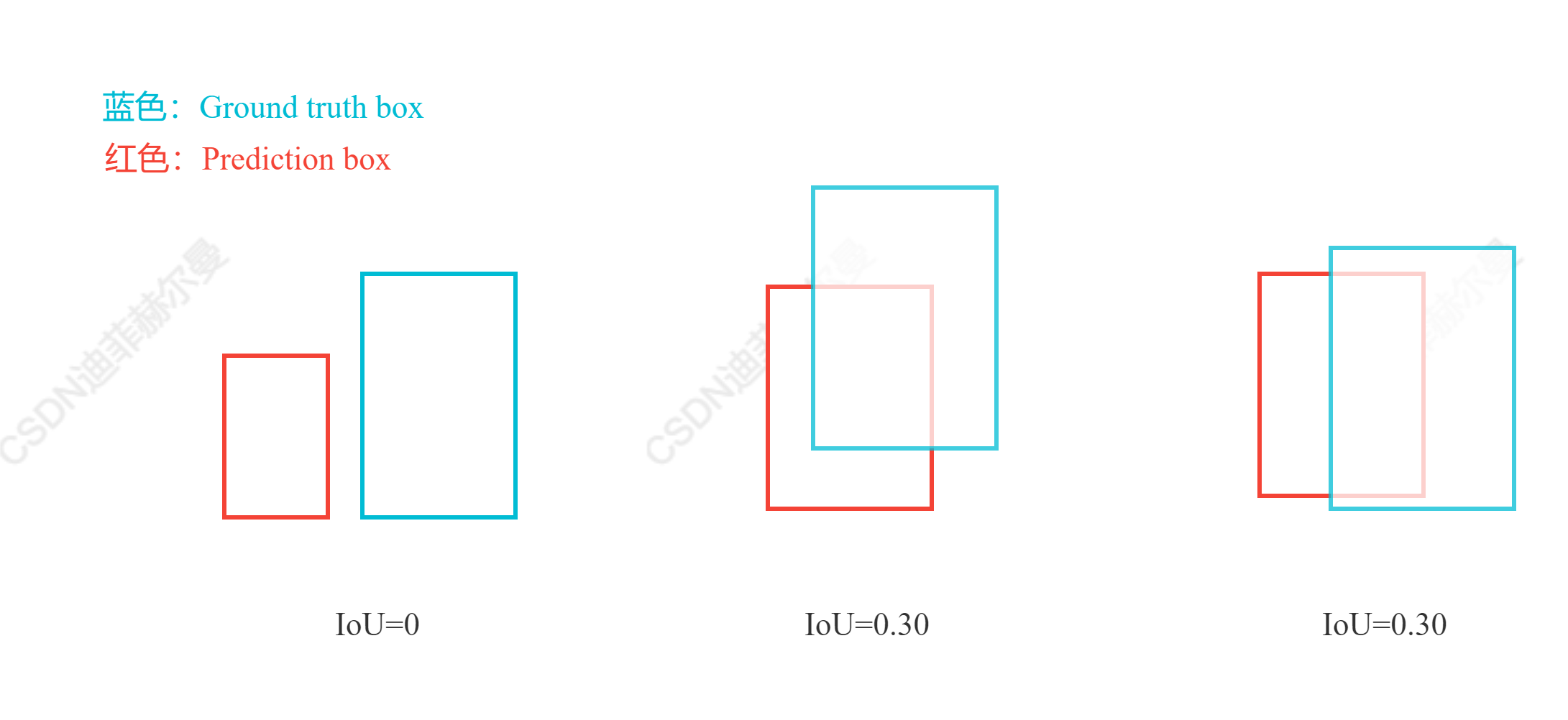
1. 当预测框和目标框不相交时，即IoU(A,B)=0时，不能反映A,B距离的远近，此时损失函数不可导，IoU Loss 无法优化两个框不相交的情况。
2. 如上图三个框，假设预测框和目标框的大小都确定，只要两个框的相交值是确定的，即其IoU值相同时，IoU值不能反映两个框是如何相交的。

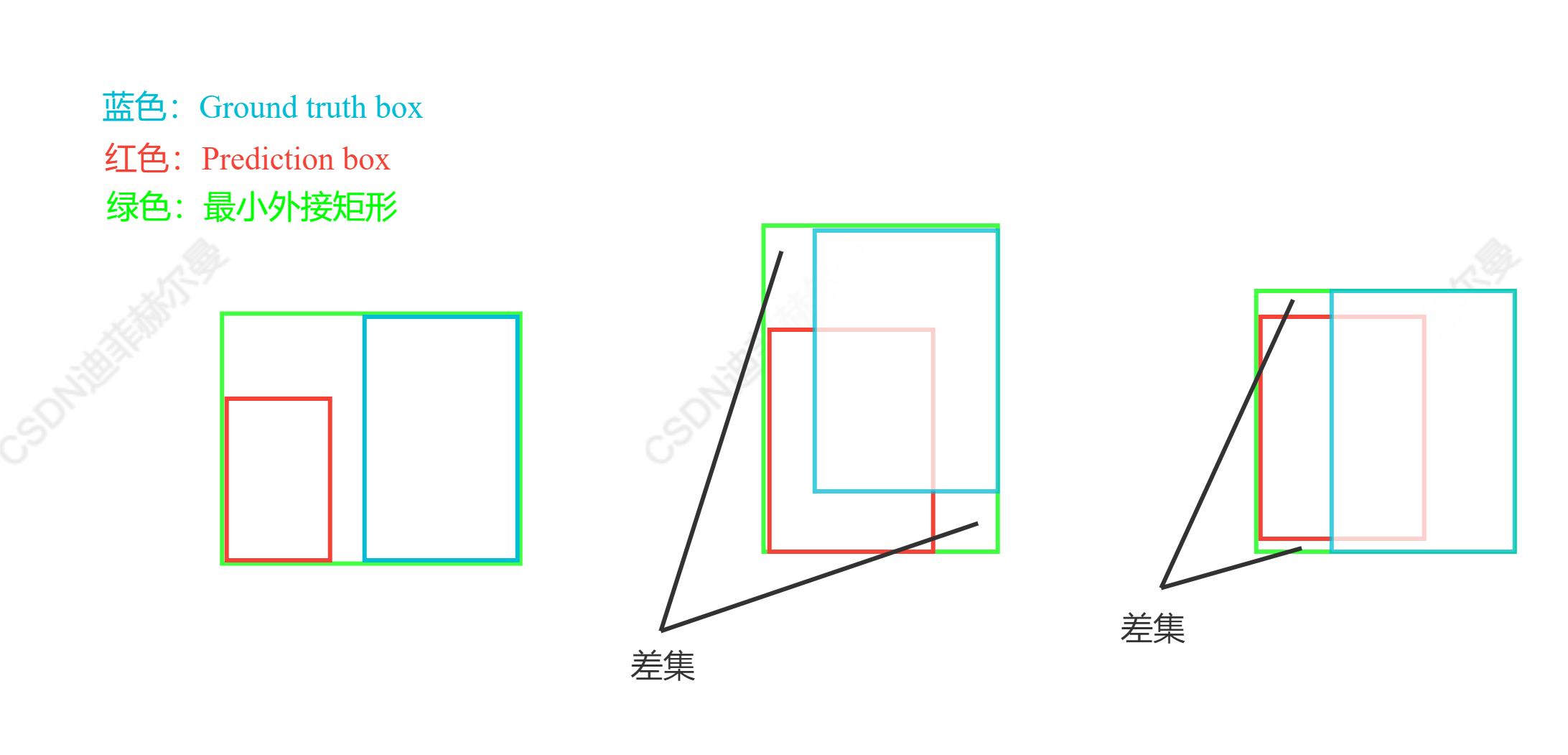
GIoU（CVPR2019）

针对

IoU

无法反映两个框是如何相交的问题，

GIoU

通过引入预测框和真实框的最小外接矩形（类似于图像处理中的闭包区域）来获取预测框、真实框在闭包区域中的比重。这样子，

GIoU

不仅可以关注重叠区域，还可以关注其他非重合区域，能比较好的反映两个框在闭包区域中的相交情况。

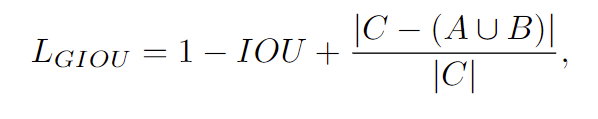
从公式上来看，

GIoU

是一种

IoU

的下界，取值范围

[-1,1]

。在两者重合的时候取最大值

1

，在两者无交集且无限远的时候取最小值

-1

。因此，与

IoU

相比，

GIoU

是一个比较好的距离度量指标。

DIoU（AAAI2020）

虽然

GIoU

通过引入闭包区域缓解了预测框与真实框相交位置的衡量问题，但其实际上仍存在两个问题：

1. 对每个预测框与真实框均要去计算最小外接矩形，计算及收敛速度受到限制
2. 当预测框在真实框内部时，GIoU退化为IoU，也无法区分相对位置关系

因此，考虑到

GIoU

的缺点，

DIoU

在

IoU

的基础上直接回归两个框中心点的欧式距离，加速了收敛速度。

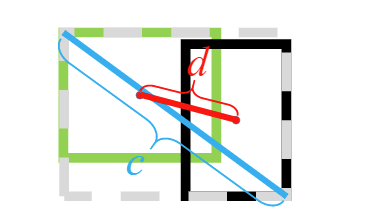
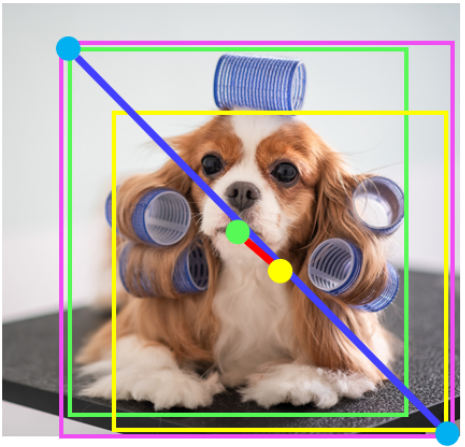
DIoU

的惩罚项是基于中心点的距离和对角线距离的比值。这样就避免了

GIoU

在两框距离较远时产生较大闭包时所造成的

Loss

值较大而难以优化的情况。

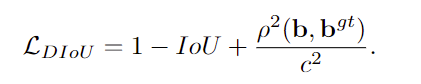
CIoU（AAAI2020）

虽然

DIoU Loss

通过中心点回归缓解了两框距离较远时难优化的问题，但

DIoU Loss

仍存在两框中心点重合，但宽高比不同时，

DIoU Loss

退化为

IoU Loss

的问题。因此，为了得到更加精准的预测框，

CIoU

在

DIoU

的基础上增加了一个影响因子，即增加了预测框与真实框之间长宽比的一致性的考量。

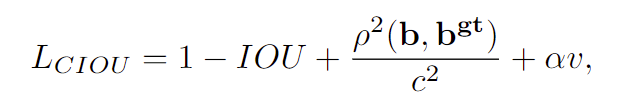
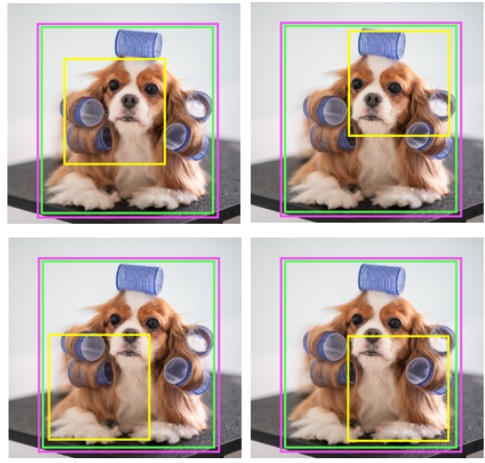
比如上面三种情况，目标框包裹预测框，本来

DIoU

可以起作用。

但预测框的中心点的位置都是一样的，因此按照

DIoU

的计算公式，三者的值都是相同的。

CIoU Loss

虽然考虑了边界框回归的重叠面积、中心点距离及长宽比。但是其公式中的v反映的时长宽比的差异，而不是宽高分别与其置信度的真实差异，所以有时会阻碍模型有效的优化。

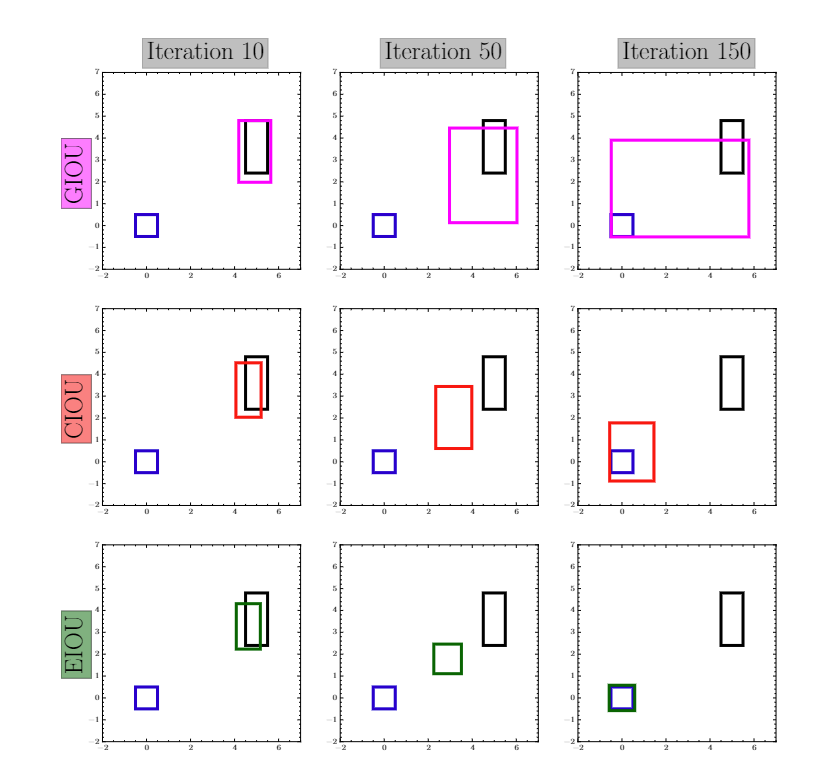
EIoU（arXiv2021）

EIoU

在

CIoU

的基础上将长宽比拆开，明确地衡量了三个几何因素的差异，即重叠区域、中心点和边长，同时引入

Fcoal loss

解决了难易样本不平衡的问题。

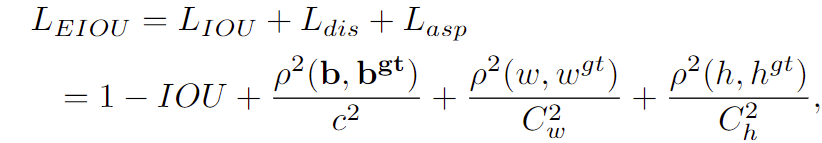
αIoU（NeurlPS2021）

αIoU

将现有的基于

IoU

的损失进行了一个推广

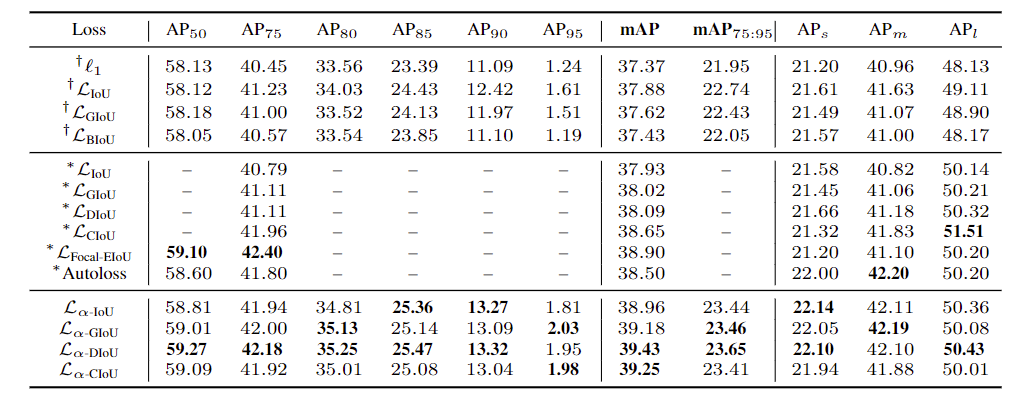
使得

αIoU

可以显着超越现有的基于

IoU

的损失，通过调节

α

，使探测器更灵活地实现不同水平的

bbox

回归精度，并且

αIoU

对小数据集和噪声的鲁棒性更强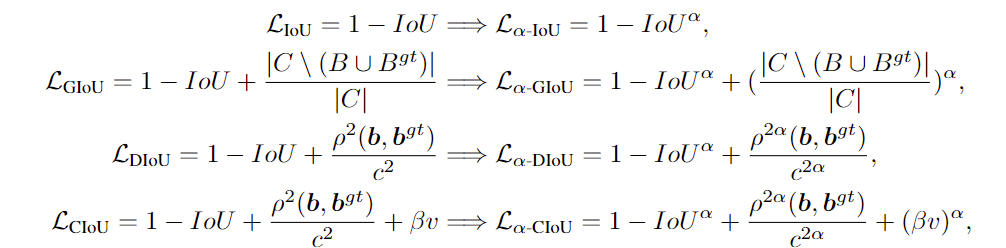

SIoU（arXiv2022）

传统的目标检测损失函数依赖于边界框回归指标的聚合，例如预测框和真实框（即

GIoU、CIoU、ICIoU

等）的距离、重叠区域和纵横比。然而，迄今为止提出和使用的方法都没有考虑期望的真实框和预测框之间不匹配的方向。这种不足导致收敛速度较慢且效率较低，因为预测框在训练过程中可能会“四处游荡”，最终会产生一个更差的模型。

SIoU

提出了一种新的损失函数，重新定义了惩罚度量，考虑了期望回归之间的向量夹角。

SIoU

损失函数由4个成本函数组成

• Angle cost

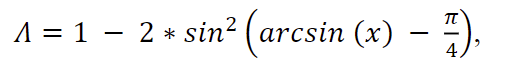
• Distance cost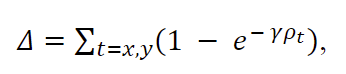
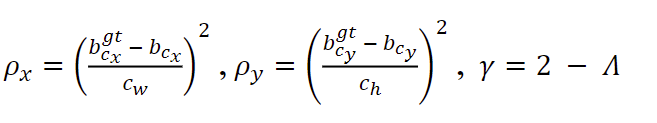
• Shape cost

• IoU cost

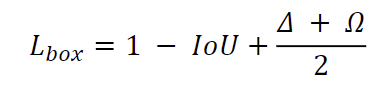
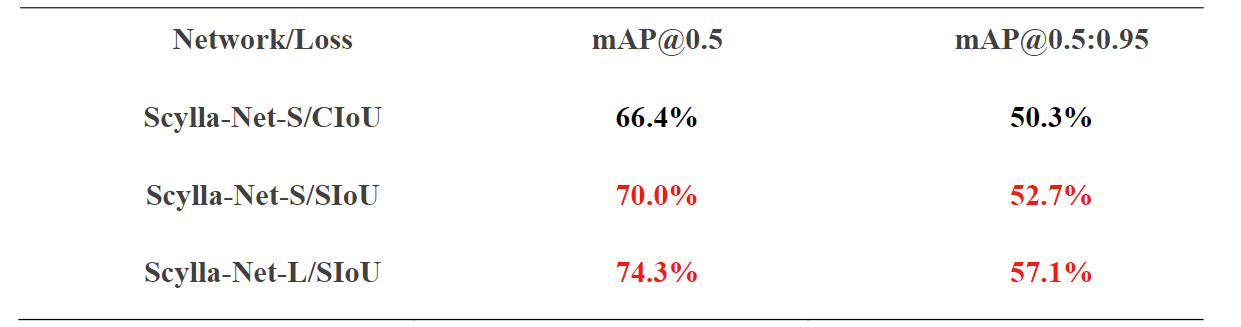
将

SIoU 

应用于

COCO-train/COCO-val

与其他损失函数相比，提高了

+2.4%

(mAP@0.5:0.95) 和 +3.6%(mAP@0.5)

各IoU源代

IoU

import numpy as np
defIou(box1, box2, wh=False):if wh ==False:
    xmin1, ymin1, xmax1, ymax1 = box1
    xmin2, ymin2, xmax2, ymax2 = box2
    else:
    xmin1, ymin1 =int(box1[0]-box1[2]/2.0),int(box1[1]-box1[3]/2.0)
    xmax1, ymax1 =int(box1[0]+box1[2]/2.0),int(box1[1]+box1[3]/2.0)
    xmin2, ymin2 =int(box2[0]-box2[2]/2.0),int(box2[1]-box2[3]/2.0)
    xmax2, ymax2 =int(box2[0]+box2[2]/2.0),int(box2[1]+box2[3]/2.0)# 获取矩形框交集对应的左上角和右下角的坐标（intersection）
    xx1 = np.max([xmin1, xmin2])
    yy1 = np.max([ymin1, ymin2])
    xx2 = np.min([xmax1, xmax2])
    yy2 = np.min([ymax1, ymax2])# 计算两个矩形框面积
    area1 =(xmax1-xmin1)*(ymax1-ymin1) 
    area2 =(xmax2-xmin2)*(ymax2-ymin2)
    inter_area =(np.max([0, xx2-xx1]))*(np.max([0, yy2-yy1]))#计算交集面积
    iou = inter_area /(area1+area2-inter_area+1e-6)#计算交并比return iou

GIoU

defGiou(rec1,rec2):#分别是第一个矩形左右上下的坐标
    x1,x2,y1,y2 = rec1 
    x3,x4,y3,y4 = rec2
    iou = Iou(rec1,rec2)
    area_C =(max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
    area_1 =(x2-x1)*(y1-y2)
    area_2 =(x4-x3)*(y3-y4)
    sum_area = area_1 + area_2

    w1 = x2 - x1   #第一个矩形的宽
    w2 = x4 - x3   #第二个矩形的宽
    h1 = y1 - y2
    h2 = y3 - y4
    W =min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)#交叉部分的宽
    H =min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)#交叉部分的高
    Area = W*H    #交叉的面积
    add_area = sum_area - Area    #两矩形并集的面积

    end_area =(area_C - add_area)/area_C    #闭包区域中不属于两个框的区域占闭包区域的比重
    giou = iou - end_area
    return giou

DIoU

defDiou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    dious = torch.zeros((rows, cols))if rows * cols ==0:#return dious
    exchange =Falseif bboxes1.shape[0]> bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        dious = torch.zeros((cols, rows))
        exchange =True# #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
    w1 = bboxes1[:,2]- bboxes1[:,0]
    h1 = bboxes1[:,3]- bboxes1[:,1] 
    w2 = bboxes2[:,2]- bboxes2[:,0]
    h2 = bboxes2[:,3]- bboxes2[:,1]
    
    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 =(bboxes1[:,2]+ bboxes1[:,0])/2 
    center_y1 =(bboxes1[:,3]+ bboxes1[:,1])/2 
    center_x2 =(bboxes2[:,2]+ bboxes2[:,0])/2
    center_y2 =(bboxes2[:,3]+ bboxes2[:,1])/2

    inter_max_xy = torch.min(bboxes1[:,2:],bboxes2[:,2:]) 
    inter_min_xy = torch.max(bboxes1[:,:2],bboxes2[:,:2]) 
    out_max_xy = torch.max(bboxes1[:,2:],bboxes2[:,2:]) 
    out_min_xy = torch.min(bboxes1[:,:2],bboxes2[:,:2])

    inter = torch.clamp((inter_max_xy - inter_min_xy),min=0)
    inter_area = inter[:,0]* inter[:,1]
    inter_diag =(center_x2 - center_x1)**2+(center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy),min=0)
    outer_diag =(outer[:,0]**2)+(outer[:,1]**2)
    union = area1+area2-inter_area
    dious = inter_area / union -(inter_diag)/ outer_diag
    dious = torch.clamp(dious,min=-1.0,max=1.0)if exchange:
        dious = dious.T
    return dious

CIoU

defbbox_overlaps_ciou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    cious = torch.zeros((rows, cols))if rows * cols ==0:return cious
    exchange =Falseif bboxes1.shape[0]> bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        cious = torch.zeros((cols, rows))
        exchange =True

    w1 = bboxes1[:,2]- bboxes1[:,0]
    h1 = bboxes1[:,3]- bboxes1[:,1]
    w2 = bboxes2[:,2]- bboxes2[:,0]
    h2 = bboxes2[:,3]- bboxes2[:,1]

    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 =(bboxes1[:,2]+ bboxes1[:,0])/2
    center_y1 =(bboxes1[:,3]+ bboxes1[:,1])/2
    center_x2 =(bboxes2[:,2]+ bboxes2[:,0])/2
    center_y2 =(bboxes2[:,3]+ bboxes2[:,1])/2

    inter_max_xy = torch.min(bboxes1[:,2:],bboxes2[:,2:])
    inter_min_xy = torch.max(bboxes1[:,:2],bboxes2[:,:2])
    out_max_xy = torch.max(bboxes1[:,2:],bboxes2[:,2:])
    out_min_xy = torch.min(bboxes1[:,:2],bboxes2[:,:2])

    inter = torch.clamp((inter_max_xy - inter_min_xy),min=0)
    inter_area = inter[:,0]* inter[:,1]
    inter_diag =(center_x2 - center_x1)**2+(center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy),min=0)
    outer_diag =(outer[:,0]**2)+(outer[:,1]**2)
    union = area1+area2-inter_area
    u =(inter_diag)/ outer_diag
    iou = inter_area / union
    with torch.no_grad():
        arctan = torch.atan(w2 / h2)- torch.atan(w1 / h1)
        v =(4/(math.pi **2))* torch.pow((torch.atan(w2 / h2)- torch.atan(w1 / h1)),2)
        S =1- iou
        alpha = v /(S + v)
        w_temp =2* w1
    ar =(8/(math.pi **2))* arctan *((w1 - w_temp)* h1)
    cious = iou -(u + alpha * ar)
    cious = torch.clamp(cious,min=-1.0,max=1.0)if exchange:
        cious = cious.T
    return cious

参考文献

https://mp.weixin.qq.com/s/jLnde0Xms-99g4z16OE9VQ

DIoU、CIoU、GIoU、IoU再理解结合代码

IoU：《UnitBox: An Advanced Object Detection Network》

GIoU：《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》

D/C IoU：《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》

EIoU：《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》

αIoU：《Alpha-IoU: A Family of Power Intersection over Union Losses for Bounding Box Regression》

SIoU：《SIoU Loss: More Powerful Learning for Bounding Box Regression》