多旅行商问题——公式和求解过程概述

英文：The multiple traveling salesman problem an overview of formulations and solution procedures

摘要：

多旅行商问题（mTSP）是著名旅行商问题（TSP）的推广，其中允许在解中使用多个旅行商。此外，MTSP的特点似乎更适合实际应用，通过加入一些附加的侧面约束，也可以将问题扩展到各种各样的车辆路径问题（VRP）。虽然TSP和VRP有大量文献，但MTSP并没有得到同样的重视。本次调查的目的是回顾该问题及其实际应用，强调一些公式，并描述针对该问题提出的精确和启发式解决程序。

1、引言

著名的旅行推销员问题（TSP）的一个推广就是多旅行推销员问题（mTSP），该问题包括确定一组销售人员的路线，所有销售人员都从家乡（仓库）出发并返回。虽然TSP受到了广泛的关注，但对mTSP的研究还很有限。本文旨在回顾有关MTSP的现有文献，重点是实际应用、整数规划公式（ILPFs）和专门为此问题设计的解决程序。

论文的其余部分将按以下步骤进行：以下部分正式定义了问题，并提出了一些重要的变化。第3节描述了文献中报告的MTSP的实际应用，并探讨了其与其他类型问题的联系。第4-6节分别介绍了编程公式、精确解和启发式解过程。第7节描述了解决该问题的基于转换的方法。最后，第8节给出了一些结论和进一步的评论。

2、问题定义和变化

mTSP通常可以定义如下：给定一组节点，让m个销售人员位于单个仓库节点。要访问的其余节点（城市）称为中间节点。然后，mTSP包括为所有m个销售人员查找行程，他们都在站点开始和结束，这样每个中间节点只访问一次，并且访问所有节点的总成本最小化。可以根据距离、时间等定义成本指标。问题的可能变化如下：

单站与多站：在单站的情况下，如果存在多个站点，且每个站点都有多个销售人员，则所有销售人员在一个点开始和结束其行程，销售人员可以在完成行程后返回其原始仓库，也可以返回任何仓库，但限制条件是，在所有行程结束后，每个仓库的销售人员初始数量保持不变。前者称为固定目的地案例，而后者称为非固定目的地案例。

销售人员数量：问题中的销售人员数量可能是有界变量，也可能是先验固定的。

固定费用：当问题中的销售人员数量不固定时，每当在解决方案中使用该销售人员时，每个销售人员通常都会产生相关的固定成本。在这种情况下，解决方案中要激活的销售人员数量的最小化也可能值得关注。

时间窗口：在此变体中，需要在特定的时间段访问某些节点，称为时间窗口。这是mTSP的一个重要扩展，被称为带时间窗的多旅行商问题（mTSPTW）。mTSPTW可以立即应用于校车、船舶和航空公司的调度问题。

其他特殊限制：这些限制可能与每个销售人员访问的节点数量、销售人员旅行的最大或最小距离或其他特殊限制有关。

MTSP可被视为VRP的简单版，取消了容量限制。这意味着，通过为销售人员（车辆）分配足够大的容量，为VRP提出的所有配方和解决方案方法也有效并适用于mTSP。然而，由于本次审查仅针对MTSP，我们将不描述VRP的现有研究。读者可以参考托斯和维戈的书[1]，了解关于这一主题的详细论述。另一方面，当只有一个销售人员时，MTSP将简化为众所周知的TSP，对此有大量的研究（例如[2-5]）。由于TSP是mTSP的一个特例，本文所描述的所有公式和算法也适用于前一个问题。

在本文中，我们将只专注于专门针对MTSP进行的研究。以下部分介绍了一些应用程序，以证明该问题的实际重要性

3、应用程序和与其他问题的连接

本节进一步细分为三个部分。第一部分介绍了MTSP的主要实际应用。第二部分指出了MTSP与其他问题的关系。第三部分具体论述了MTSP与著名的VRP之间的联系。

3.1、主要应用

与TSP相比，MTSP更适合模拟实际情况，因为它能够处理多个销售人员。这些情况主要出现在各种路由和调度问题中。下面介绍了一些报告的应用程序。

1）印刷机调度：

戈伦斯坦（Gorenstein）[6]提出的MTSP的主要应用之一，是为多版本期刊安排印刷机。在这里，有五对圆筒，在这五对圆筒之间，纸卷和页面的两面同时打印。有三种形式，即4页、6页和8页的形式，用于打印版本。调度问题包括决定哪个窗体将用于哪个运行以及每次运行的长度。在中期战略计划词汇中，换板成本是城市间成本。在类似的情况下，正如卡特和拉格斯代尔最近指出的那样，中期战略计划还可用于制定报纸预印插页广告的制作时间表。在这个问题上，广告商需要在报纸中插入特定的广告或随报纸一起发布，以便分发到不同的地理区域。每个特定区域接收相同的广告集。在MTSP中，地区对应城市，每条生产线对应一名销售人员。

2）机组调度：

Svestka和Huckfeldt【8】报告了不同分行之间的存款结转申请。在这里，存款需要在分行提取，然后由一组信使返回中央办公室。问题是以最低的总成本确定信使的路线。Lenstra和Rinnoy Kan【9】描述了两个类似的应用，其中第一个应用包括查找技术人员的路线，他们必须访问荷兰北部的电话亭。第二个应用程序涉及设计访问乌得勒支200个邮箱的车辆路线，以便使用的车辆数量最少。Zhanget al.（10）报告了mTSP在团队调度中的另一个应用，他研究了将多组摄影师安排到大量中小学的问题。

3）校车路线问题：

Angel等人【11】将公交车调度问题作为mTSP的一种变体进行了研究，并考虑了一些侧面约束。调度的目标是获得公交装载模式，从而使路线数量最小化，所有公交车行驶的总距离保持最小，没有公交车超载，并且穿越任何路线所需的时间不超过允许的最大策略。

4）面试安排：

Gilbert和Hofstra【12】描述了mTSP多周期变化的应用，其中在安排旅游经纪人和旅游业供应商之间的访谈时出现了问题。每个经纪人对应一名推销员，该推销员必须访问一组指定的摊位，摊位由一组T城市表示。

5）任务规划：

任务规划通常出现在自主移动机器人的环境中，其中各种应用包括建筑、军事侦察、仓库自动化、邮局自动化和行星探索。任务计划包括确定每个机器人的最佳路径，以在尽可能短的时间内完成任务目标。任务规划师使用mTSP的一种变体，其中有n个机器人，m个目标必须由某个机器人访问，以及一个所有机器人最终必须返回的基地城市。Brummit和Stentz【13】报告了mTSP在任务规划中的应用，Brummit和Stentz【14】报告了mTSP在非结构化环境中的应用。Yu等人[15]在合作机器人领域将自主机器人的规划建模为mTSP的一个变体。同样，如Ryanet等人【16】所研究的，无人机应用规划中出现的路由问题可以建模为带时间窗的mTSP。

5）热轧计划：

在钢铁工业中，必须在热轧带钢轧机上安排生产班次的订单，以使生产顺序中的总过渡（设置）成本最小化。Tang等人【17】给出了将中国某钢铁厂遇到的此类问题建模为mTSP的最新应用。这里，订单对应于城市，两个城市之间的距离是两个订单之间生产转换的惩罚成本。该模型的求解将为热轧带钢生产线提供一个完整的生产计划。

6）全球导航卫星系统测量网的设计：

Saleh和Chelouah[18]研究的MTSP的一个最新和有趣的应用出现在全球导航卫星系统（GNSS）测量网络的设计中。全球导航卫星系统是一种天基卫星系统，覆盖全球所有地点，在灾害预警和管理、环境和农业监测等实际应用中至关重要。测量的目的是利用卫星设备确定地球上和地球上方未知点的地理位置。放置接收器的这些点通过一系列观察会议进行协调。当存在多个接收器或多个工作周期时，可以将为接收器寻找会话的最佳顺序的问题表示为mTSP。关于技术细节，读者可以参考Saleh和Chelouah。

3.2. 与其他问题的关系

上述实际情况可以直接建模为MTSP，必要时进行一些小的扩展。然而，MTSP也很重要，因为它是解决更一般性问题的一个次级问题。正如Okonjo Adigwe（19）所讨论的，这样一个问题的一个例子是平衡销售人员之间的工作量。本文提出了一种基于mTSP的建模和求解方法，以解决带有额外限制的工作负荷调度问题，例如行程时间的下限和上限以及每个销售人员的总重量。另一个例子是Calvo和Cordone调查的夜间安全服务问题【20】。该问题包括将职责分配给若干警卫，这些警卫将在给定的一组位置执行常规检查服务。此外，还应遵守一些限制，如容量和时间窗口。为解决该问题提供了一种分解方法，其中一个子问题是mTSPTW。

MTSP也是船舶运营计划中码头起重机调度的一个子问题。Kim和Park【21】研究了这个问题，他们利用mTSP在为解决这个问题提供的分枝定界算法中找到了紧下界。正如Macharis和Bontekoning所指出的那样，具有时间窗的MTSP可用于建模多式联运货运问题。在这种情况下，Wang和Regan【23】将当地卡车的提货和交付问题建模为具有时间窗口的非对称mTSP。该问题的解是通过使用时间窗离散化的迭代方法获得的。

正如Basu等人所指出的那样，MTSP的一个有趣的应用在于协调多个物体的运动的问题。这种问题可能出现在电子电路的组装、分布式系统的内存管理以及结构化空间（如仓库）中移动机器人的协调中。该问题定义在一个矩形网格上，该网格被划分为若干个正方形。正方形可以包含对象，也可以是空白。然后，可以使用mTSP模型在具有多个空格的网格上找到对象的最佳移动。

3.3、与VBR的联系

由于其紧密的联系，mTSP还可以用于解决几种类型的VRP。例如，Mole等人[25]讨论了几种车辆路径算法，并提出了一种启发式方法，该方法搜索由mTSP的大量可行解构成的解空间。在类似的情况下，mTSP可用于计算在姿态约束VRP中为一组客户服务所需的最小车辆数量，其中每个客户都有相关的非负需求，并且每辆车的行驶距离不能超过预定义的距离（见[26,27]）。在具有随机服务时间的VRP的两阶段求解过程中，mTSP也是第一阶段的问题，其中第一阶段的解用于计算第二阶段的预期成本。Hadjiconstantinou和Roberts对此进行了进一步讨论【28】。MTSP和难民问题解决方案的密切联系进一步激发了人们对前一个问题的兴趣。事实上，拉尔夫（Ralphs）[29]提到，在实践中出现的VRP实例可能非常难以解决，因为潜在的mTSP本质上也是复杂的。这一声明反过来又提出了有效解决MTSP的必要性，以应对现实生活中出现的大规模VRP。

MTSP还与提货和交货问题（PDP）有关，因为后者是Ruland和Rodin指出的前者的受限版本【30】。PDP包括确定一组车辆的最佳路线，以满足客户请求，这些请求由起点-终点对指定。另外的限制是，每次旅行的出发地必须在目的地之前。如果要在特定的时间间隔内为客户提供服务，那么问题就变成了带时间窗口的PDP（PDPTW）。Mitrovic Minícetal也表明了这一点。【31】，如果每个请求的起点和终点重合，PDPTW将减少为mTSPTW。

3.4、讨论

作为本节所述应用程序的总结，我们提供了表1，其中显示了mTSP的可能应用领域，其中第一列显示了应用程序上下文，第二列显示了特定类型的应用程序。

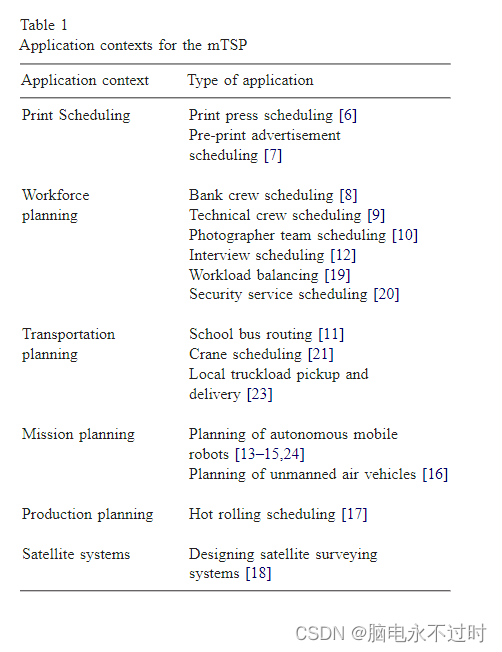
如表1所示，mTSP可用于各种规划/调度类型的问题，从印刷品调度到运输和任务规划。因此，MTSP不仅对理论利益很重要，而且对其模拟许多战略决策问题的能力也很重要。

虽然MTSP是对VRP的简易版，所以VRP开发的所有解决方法对前者都有效，但这些方法可能并不总是有效的，也不总是很适合MTSP。事实上，由于这些程序不是专门为MTSP定的，在解决过程中可能会出现退化，造成不必要的困难。虽然不多，但文献中提出了一些专门为MTSP量身定制的解决程序。这些程序通常包括基于整数线性规划公式的算法和问题到Tsp的转换。

在第4节中，我们首先介绍了MTSP的几个整数规划公式。然后，我们在第5节中概述了为MTSP制定的精确解程序。启发式解决程序和mTSP到标准TSP的转换将在后续章节中介绍。

4、整数规划公式

为MTSP提出了不同类型的整数规划公式。在介绍之前，一些技术定义如下。mTSP在图G=（V，A）上定义，其中V是n个节点（顶点）的集合，A是弧（边）的集合。设C=（cij）是与A相关的成本（距离）矩阵。当cij=cji时，矩阵C称为对称矩阵，∀（i，j）∈A, 否则为不对称矩阵。如果cij+cjk>=cik，∀i、 j，k∈V、 C，则表示满足三角形不等式。

文献早些时候提出了MTSP的各种整数规划公式，其中有基于分配的公式、基于树的公式和基于三指标流的公式。现在，我们将在下面的部分中介绍它们。

4.1、基于赋值的整数规划公式（Assignment-based integer programming formulations）

MTSP通常采用基于分配的双指数整数线性规划公式。我们首先定义以下二进制变量：

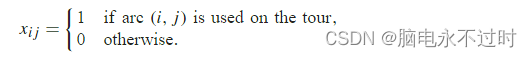
然后，可以给出mTSP基于分配的有向整数线性规划公式的一般方案如下：

其中（3）、（4）和（6）是常见的分配约束条件，（1）和（2）确保准确无误的乘客离开并返回节点1（车辆段）。虽然（1）、（3）和（4）已经暗示了约束（2），但为了完整性，我们在这里给出了它们。约束（5）用于预防次行程，次行程是在中间节点之间形成且未连接到原点的退化行程。这些约束被命名为子循环消除约束（SECs）。

文献中已经为MTSP提出了若干SEC。第一组SEC基于Dantzig等人[32]最初提出的TSP，但也适用于mTSP。这些约束可以显示如下：

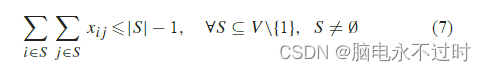
或者在以下情况下：

约束条件（7）或（8）对解决方案提出了连通性要求，即防止形成基数S的小项，不包括仓库。不幸的是，这两类约束都随着节点数的增加呈指数增长，因此无论是直接解决问题还是线性规划松弛都不实用。Miller等人【33】通过引入O（n2）个额外的连续变量，即节点电位，从而产生多项式秒数，从而克服了这个问题。其秒数如下（以MTZ秒表示）：

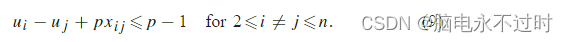
这里，p表示任何销售人员都可以访问的最大节点数。每个节点的节点电位指示tour中相应节点的顺序。

Svestka和Huckfeldt提出了mTSP的另一组SEC，它们需要用新行和新列来扩充原始成本矩阵[8]。然而，Gavish[34]表明，对于m>2，他们的约束是不正确的，并提供了如下正确的约束：

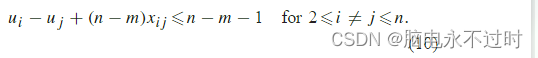
还为MTSP提出了其他以MTZ为基础的SEC。以下限制是由于Kulkarni和Bhave【35】（以KB秒表示）：

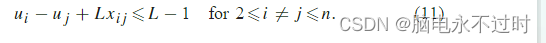
在这些约束中，L与（9）中的p相同。很明显，MTZ秒和KB秒是等效的。

最近，MTSP的一组SECs由Kara和Bektas负责【36】。这些约束不同于其他现有的Sec，因为它包含了额外的边约束，可以用来对销售人员访问的节点数（K）施加下限。这种下限可能出现在收款的情况下，每个销售人员可能需要至少拜访客户来提货等。这些限制条件如下：

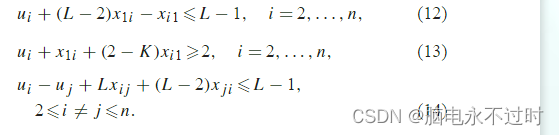
这里，L的含义与（11）中的相同。约束（12）和（13）用于对销售人员访问的节点数施加限制。

4.2. 拉波特和诺伯特公式 （Laporte and Nobert’s formulation）

拉波特（Laporte）和诺伯特（Nobert）[37]分别针对不对称和对称成本结构提出了MTSP的两个公式，并考虑了解决方案中使用的每个销售人员的共同固定成本f。这些公式包括指数秒数，因此用于切割平面框架。这些公式也基于之前定义的两个指数变量xij。非对称MTSP的表述如下：

此公式是一个纯二进制整数公式，其目标是最小化旅行的总成本以及解决方案中使用的销售人员总数。请注意，约束（16）和（17）是标准分配约束，约束（18）是Dantzig等人的SECs。[32]。唯一不同的约束是（15），它对仓库节点施加程度约束。

拉波特和诺伯特的对称MTSP公式如下：

关于这个公式的有趣问题是，由于变量x1j可以是0、1或2，它不是一个纯二进制整数公式。请注意，变量xij仅为i<j定义，因为问题是对称的，并且只有一个变量足以表示解决方案中使用的每条边。约束（21）和（22）分别是站点节点和中间节点上的度约束。其他约束如前所述。

4.3、基于k度中心树的公式（k-Degree centre tree-based formulation）

对称mTSP的公式由Christofides等人提出。该公式基于k度中心树（k-DCT），这是一棵树，其中仓库正好有k个相邻弧。该公式也可用于推导VRP的下界。在公式中，边集的划分如下所示（这种表示是由于Laporte[39]）。

E0：不属于解决方案的边，

E1：形成K-DCT的边。

E2：靠近仓库的边缘（| E2 |=y，0 < y < m），

E3：与仓库不相邻的边缘（| E3 |=m−y） 。

我们为该公式定义了以下二进制变量：

在公式中，（S，S）表示所有边的集合，一端在S中，另一端在S中。目标是最小化解决方案中使用的每条边的总成本，其中cl表示在解决方案中使用边l的成本。约束（27）规定树是连接的。此外，约束条件（28）意味着k=2m−y仓库段附近的弧。其他约束（29）–（31）与解决方案中的弧数相关。最后，约束条件（32）意味着除仓库点以外的每个节点的阶数为2。

4.4. 基于流的公式（A flow-based formulatio）

赫里斯托菲德斯（Christofides）等人[38]提出了一种基于MTZ-SECs的三指数VRP模型。可以通过排除能力和成本限制，使其表述适应MTSP。虽然这一公式是为VRP提出的，但我们希望将这一公式引入MTSP，因为它是唯一具有有趣特征的三个指数公式。在给出公式之前，我们定义了以下三个指数变量：

（如果k在节点i之后立即访问节点j）。

然后可给出如下公式：

约束条件（35）规定每个客户应访问一次，而（36）是流量守恒约束条件，确保销售人员访问客户后，也必须离开同一客户。约束条件（37）确保每辆车只使用一次，（38）是基于MTZ的SEC对三指标模型的扩展。不幸的是，由于即使对于中等规模的MTSP，该公式中的变量数量也是巨大的，因此直接将该公式求解为最优可能不太现实。

5、精确算法

拉波特（Laporte）和诺伯特（Nobert）[37]提出了一种基于问题某些约束松弛的算法，这是第一种直接求解mTSP的方法，无需对TSP进行任何转换（见第7节）。这种直接方法的动机是，转化后的问题将包含许多等效的次优解决方案，因此将更难解决。他们考虑的问题是一个与每个销售人员相关的固定成本f的MTSP，该计划在解决方案中使用销售人员时激活。该算法包括通过最初放松SECs来解决问题，并在获得整数解后检查是否违反了任何SECs。如果是这种情况，则会引入一个约束来删除此类子任务。这种方法被称为直线算法。与此方法相反，还考虑了一种反向算法，其中再次放松秒数，但在达到整数解之前执行检查。作者报告说，反向算法获得了更好的计算结果，在CYBER 173计算机上解决了多达100个节点的问题。就mTSP的求解策略而言，本文的一个有趣的结果是：算法的求解时间随着m的增加而减少，但随着m的增加，求解变换后的问题所需的时间更长。这一结果可能是由于变换问题的退化性，退化性随m的增大而增大。

Ali和Kennington【40】提出了一种基于分支定界的非对称TSP算法。该算法使用拉格朗日松弛度约束和次梯度算法来求解拉格朗日对偶。该算法在大小为n=100的非对称问题以及大小为n=59的对称问题和欧几里德问题上进行了测试。

Gavish和Srikanth首次尝试将大规模对称MTSP求解到最优状态【41】。该算法是一种分枝定界法，其下界是通过松弛度约束构造的拉格朗日问题得到的。拉格朗日问题使用跨越所有节点的度约束最小生成树来解决。采用次梯度优化方法更新拉格朗日乘子，并采用快速灵敏度分析技术减小问题规模。通过广泛的计算分析，作者能够在IBM 3032和IBM 3081D计算机上使用此算法解决500个节点和m=2,4,6,8,10的非欧几里德问题，以及100个城市和10名销售人员的欧几里德问题。结果表明，拉格朗日松弛法得到的整数间隙随着问题规模的增大而减小，对于所有n>400的问题，结果都是零。欧几里德问题被证明比非欧几里德问题更难。该算法还与Ali和Kennington[40]以及Laporte和Nobert[37]的m算法进行了比较，作者表示他们的算法“似乎明显优于”。对TSP的转换也进行了测试，但对于较大的m值（m>4），转换后的问题碰巧比原始问题更难解决。

针对mTSP提出的另一种精确解方法是由Gromicho等人提出的。本文研究了具有固定推销员数的非对称mTSP问题。由于QA问题在多项式时间内是可解的，因此该算法基于通过松弛秒获得的准赋值（QA）松弛。应用加法定界程序来加强通过不同r-树状和r-反树状松弛获得的下界，该程序嵌入到分支定界框架中。我们观察到，加性边界程序在改善下限方面有显著效果，QA松弛产生的下限很差。所提出的分枝定界算法优于标准的分枝定界方法，在节点数方面QA松弛，从减少10%到减少10倍不等。观察到对称实例可以产生更大的改进。使用一台运行频率为25 MHz的80386 CPU的IBM PS/70计算机，通过这种方法解决的最大实例有120个节点，销售人员的数量从2个到12个不等

6、启发式求解过程（Heuristic solution procedure）

解决带有某些附加条件的TSP中的m-tours问题的第一个启发式方法是Russell[44]，尽管解决过程是基于将问题转化为扩展图上的单个TSP。该算法是最初为TSP开发的Lin和Kernighan启发式算法的扩展版本。另一个基于mTSP交换程序的启发式方法是givenby Potvin等人提出的。

Fogel[47]提出了一种利用进化规划求解mTSP的并行处理方法。该方法考虑两个推销员和一个目标函数，该目标函数最小化每个推销员的路线长度之间的差异。解决了25个和50个城市的问题，值得注意的是，进化方法获得了非常好的近似最优解

也有人提出了几种人工神经网络（NN）方法来解决mTSP，但它们通常是针对TSP提出的方法的扩展版本。Wacholder等人[48]将Hopfield Tank ANN模型扩展到mTSP，但他们的模型过于复杂，无法保证可行的解决方案[49]。Hsu等人[50]提出了一种基于求解m个标准TSP的神经网络方法来求解mTSP。作者表示，他们的结果优于Wacholder等人[48]。MTSP的自组织神经网络方法源于Vakhutinsky和Golden【51】，该方法基于为TSP开发的弹性网络方法。Goldstein提出了另一种用于MTSP的自组织神经网络方法【52】。Torki等人【53】描述了一种基于增强mTSP神经网络模型的VRP自组织神经网络。最近，Modares等人【54】和Somphom等人【49】开发了一种用于mTSP的自组织神经网络方法，该方法具有最小-最大目标函数，可将所有销售人员中最昂贵路线的成本降至最低。他们的方法似乎优于弹性净方法。

Zhang等人是第一个利用遗传算法（GA）解决mTSP。Tang等人[17]最近的一个应用程序使用遗传算法来解决为热轧调度开发的mTSP模型。该方法基于将问题建模为mTSP，将其转换为单个TSP，并应用改进的遗传算法获得解决方案。Yu等人【15】还使用GAs解决路径规划中的mTSP问题。

Ryan等人【16】将禁忌搜索（Tabu search）用于求解带时间窗的mTSP。作者提供了一个整数线性规划公式，但在离散事件仿真框架内通过反应式禁忌搜索算法解决了该问题。

最近，Song等人[55]提出了一种针对mTSP的扩展模拟退火方法，该方法具有与每个销售人员相关的固定成本。该方法在有400个城市和三名销售人员的mTSP上进行了测试，但在IBM PC-586（400 MHz）上需要51分钟才能解决。

Gomes和Von Zuben【56】提出了一种基于竞争学习的神经模糊系统，用于解决mTSP以及有能力的VRP。该方法采用模糊规则库引导的无监督网络学习。Soffe等人【57】实施并比较了多种进化计算算法来解决mTSP，包括使用邻域吸引子模式、用于局部邻域优化的收缩包裹算法、粒子群优化、蒙特卡罗优化、遗传算法和进化策略。

7、TSP的转换

解决mTSP的方法之一是将问题转化为标准TSP，从而能够使用为后者开发的任何算法来获得前者的解决方案。

单仓库mTSP的首批转型之一是由于Gorenstein【6】。他提出，一个有m个推销员的TSP可以用一个有（m−1） 额外的母城市，在这些城市中，为家到家的距离分配无限成本以禁止此类旅行，并且在额外的“母城市”和其他城市之间分配零成本。单个销售人员和多个销售人员问题的最小成本解决方案是相同的。然而，Svestka和Huckfeldt[8]认为，这种转换并不合适，会导致距离矩阵不必要的增加。相反，他们提出了一种变换，其中原始距离矩阵用扩充m−1新行和列，使每一新行和列都与原始距离矩阵的第一行和列重复。该算法首先解决由约束（3）和（4）定义的分配问题，并检查是否违反了任何SEC。如果存在此类违反约束，则修改距离矩阵，将违反约束引入问题，并再次解决由此产生的分配问题。该算法一直在求解此类分配问题，直到满足所有约束，并且过程以最优解结束。作者已经解决了多达60个城市的问题。作者发现的两个主要结果是，mTSP最困难的情况是一个销售员情况，当3<n/m<7时，计算时间最少。

Orloff【58】在修改的图上提供了m车辆一般路径问题（m-GRP）到GRP的一般转换。作为一个特例，它还表明求解任何mTSP都等价于变换图上的TSP解。在此基础上，提出了求解mTSP的次目标消除算法。

Bellmore和Hong[59]表明，具有m个销售人员和n个节点的非对称mTSP可以转换为具有（n+m-1）个节点的标准非对称TSP 节点。本研究还考虑了每个销售人员Ci的固定成本，仅当激活销售人员i时才会发生。Hong和Padberg[60]也进行了类似的转换，其中，考虑到固定费用，将具有m个推销员和n个节点的对称mTSP转换为具有（n+m+4）个节点的标准对称TSP。Rao[61]将Bellmore和Hong[59]给出的非对称情况下的变换推广到具有（n+m−1） 节点的标准对称TSP。Gheysens[62]给出了与Rao[61]的公式在数学上等价的公式。最后，Jonker和Volgenant【66】将对称多旅行商问题的标准转换改进为具有稀疏边配置的标准TSP。他们认为m−1仓库副本导致高度退化的转换问题，其中mTSP的最优解对应于TSP的m个最优解。作者指出，在复制仓库周围具有更稀疏的边缘配置的情况下，转换后的问题退化程度较低，并且当用于分支定界格式时，与Gavish和Srikant相比，该程序的计算工作量要小得多。

文献中还存在多仓库mTSP到标准TSP的许多转换。与我们的讨论最相关的参考文献如下：Laporte等人[63]考虑了固定目标MMP，其具有导致在分枝定界方案中使用的约束分配问题的转换。正如郭兴[64]所指出的，这是一个不完整的转换，因为由此产生的问题具有非赋值约束。对于非固定目的地情况，郭兴[64]给出了非对称多站mTSP到标准非对称TSP的完整转换。然而，Kara和Bektas[36]为此问题提出了一个多项式大小的整数线性规划模型，并表明求解转换后的问题远比求解原始问题困难。

8、结论

多旅行商问题是一个重要的理论和实践问题。首先，它概括了旅行商问题（TSP），可以从理论角度对其进行研究以更好地理解TSP。另一方面，通过引入额外的侧面约束，例如容量、距离和时间窗口约束，可以很容易地将其扩展到各种车辆路径问题（VRP）。这些讨论的自然结果揭示了MTSP在TSP和VRP背景下的明显作用，因为它将这两个重要问题联系起来。因此，MTSP本身在实际分配和路由中发挥着核心作用。不幸的是，关于这个问题及其解决方法的研究还不多。

就问题的解决而言，我们提供了表2，其中总结了为MTSP提出的现有解决程序。表的第一列表示方法的类型，而第二列表示具体的求解程序。

如表2所示，存在几种精确求解程序，主要由分枝和定界型方法组成，这些方法仅限于求解大小合理的问题。另一方面，我们观察到文献有一种启发式求解技术的趋势，其中基于神经网络的过程似乎是最流行的。还存在一些基于转换的过程。

基于将mTSP转换为标准TSP的求解过程似乎并不高效，因为生成的TSP高度退化，尤其是随着销售人员数量的增加。[37,65]中的MTSP和[36]中的多基地MTSP也指出了这一点。然而，努力减少转换问题中的简并量可能会导致高效的求解程序，这是[66]中采用的方法。目前，只要使用良好的初始边界，该问题的有效精确解程序似乎是分枝定界方法。一般来说，求解到最优的最大非对称MTSP约有500个节点，对称问题约有100个节点（假设销售人员数量有限）。为了以最佳方式解决更大的问题，我们认为，为MTSP专门定制的更好的整数规划公式和精确求解程序仍然值得注意。

就MTSP的启发式算法而言，以前的文献侧重于人工神经网络。然而，我们认为，MTSP的其他现代启发式方法值得更多关注。据我们所知，目前还没有有效的启发式算法来求解大规模MTSP。我们将进一步研究启发式算法在MTSP中的应用，这些方法对于解决VRP非常成功，例如禁忌搜索.