在本篇文章中将解释高斯混合模型（GMM）的关键部分背后的数学原理，即期望最大化（EM），以及如何将这些概念转换为Python。这个故事的重点是EM或M-Step。

注意：这不是有关端到端GMM算法的全面说明。要进行更深入的研究，请参阅我们以前翻译的文章。

期望最大化

GMM中有一系列步骤，通常称为“期望最大化”，简称“ EM”。要解释如何理解EM数学，请首先考虑您可能要处理的模型。

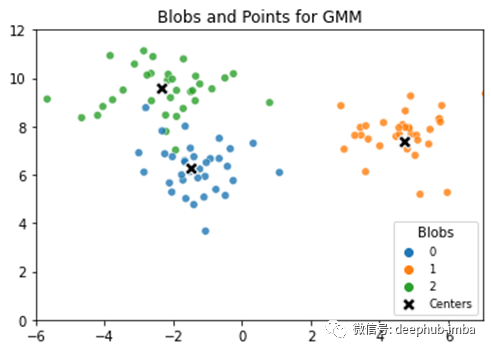
样本由图形上的点表示。这些点形成一些不同的斑点。每个斑点都有一个中心，每个点都与每个斑点的中心相距一定距离。给定GMM模型数据，目标通常是根据最接近的中心按其样本点标记其他样本。有些点距离一个或多个中心几乎相等，因此，我们希望基于某种概率来标记点。

EM用到的符号

要学习如何学习机器学习算法，您一生中需要一些希腊语。因为算法中符号基本上都是以希腊文表示的。尽管可能会想掩盖基础知识，但是对单个希腊字母的简单掌握可以帮助您理解算法中的重要概念。

算法可能会令人生畏且令人困惑。例如，乍看之下，高度集中的希腊符号有时足以使人窒息。但是不要浪费时间，我们在这里只要考虑现在要使用的符号即可

除此以外，我们也有一些英文字母在EM中代表GMM的意思。通常，英文字母围绕着希腊字母，就像小领航鱼围着大鲨鱼游动。就像小鱼一样，英文字母有一个重要的作用，它为如何解释算法提供了指导。

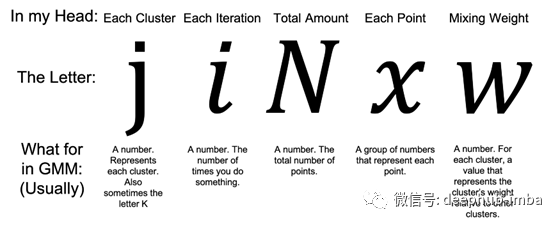
M-Step的数学解释

现在我们已经隔离了方程的每个组成部分，让我们通过检查M-Step，将它们组合成一些常用的数学短语，这些短语对于用EM语言进行对话很重要。

簇，高斯，字母J或K，有时还包括C：通常都是同一件事-如果我们有3个簇，那么您可能会听到“每个高斯”，“每个j”，“每个高斯j”或 “对于每个K组件”-这些都是谈论相同3个簇的不同方法。在数据方面，我们可以绘制（x，y）样本/点的数组，并查看它们如何形成簇。

 # a 2D array of samples [features and targets] 
 # the last column, targets [0,1,2], represent three clusters
 # the first two columns are the points that make up our features
 # each feature is just a set of points (x,y) in 2D space
 # each row is a sample and cluster label
 
 [[-7.72642091 -8.39495682  2. ]
  [ 5.45339605  0.74230537  1. ]
  [-2.97867201  9.55684617  0. ]
  [ 6.04267315  0.57131862  1. ] ...]

软分类（Soft Assignments），概率，响应度（Responsibility）：聚类的一个主要思想是我们希望为每个样本找到一个数字，以告诉我们样本属于哪个聚类。在GMM中，对于我们评估的每个样本，我们可能会返回代表“每个高斯j的响应度”，每个“软分类”或每个“概率”的值。

这些阶段通常都是关于同一件事的，但响应度与概率之间存在关键区别。

 # an array of assignment data about the 2D array of samples
 # each column represents a cluster
 # each row represents data about each sample
 # in each row, we have the probability that a sample belongs to one of three clusters - it adds up to 1 (as it should)
 # but the sum of each column is a big number number (not 1)
 
 print(assignments)
 # sample output: an array of assignment data
 [[1.00000000e+000 2.82033618e-118 1.13001412e-070]
  [9.21706438e-074 1.00000000e+000 3.98146031e-029]
  [4.40884339e-099 5.66602768e-053 1.00000000e+000]...]
 
  print(np.sum(assignments[0])
 # sample output: the sum across each row is 1
 1
 
 print(np.sum(assignments[:, 0])
 # sample output: the sum in each col is a big number that varies
 # Little Gamma: the really small numbers in each column
 # Big Gamma: the sum of each column, or 33.0 in this sample33.0

大写伽玛，小写伽玛，J，N，x和i：EM中的核心任务是为每个群集优化三组参数，或者“对于每个j，优化w（𝓌），mew（𝜇 ）和方差（𝜎）。” 换句话说，群集的权重（𝓌），群集的中心点（𝜇）和群集的方差（𝜎）是多少？

对于权重（𝓌），我们将“大写伽玛”除以特征总数。从更早的时候开始，我们就知道每个聚类j的大写伽玛只是将给定聚类的每个样本的分配值相加的结果（该数字之和不等于1）。如下图所示

对于EM期间高斯的权重参数，请考虑一些简单的事情，例如添加数字列表，然后将其除以样本总数。

对于mew （𝜇），不是像我们之前那样将所有小写伽玛加到一个小写伽玛中，而是对每个聚类j和每个样本i将小写伽玛与特征x进行矩阵乘法。如下图所示

请记住，mew只是每个簇的中心点-如果我们有3个簇，而我们的样本都是x，y坐标，那么mew将是3个x，y坐标的数组，每个簇一个。

 # for figure 4 - mew (mu)
 # same array of assignment data as before
 # each column is a cluster of little gammas
 
 print(assignments)
 [[1.00000000e+000 2.82033618e-118 1.13001412e-070]
  [9.21706438e-074 1.00000000e+000 3.98146031e-029]
  [4.40884339e-099 5.66602768e-053 1.00000000e+000]...]
 
  # the little gammas of cluster 0 is just column 0
 [[1.00000000e+000 ]
  [9.21706438e-074 ]
  [4.40884339e-099 ]...]
 
  # same array of sample data as before
 # the first two columns are the x,y coordinates
 # the last column is the cluster label of the sample
 
 print(features)
 [[-7.72642091 -8.39495682  2. ]
  [ 5.45339605  0.74230537  1. ]
  [-2.97867201  9.55684617  0. ]
  [ 6.04267315  0.57131862  1. ] ...]
 
  # for features, we just need its points
 [[-7.72642091 -8.39495682  ]
  [ 5.45339605  0.74230537  ]
  [-2.97867201  9.55684617  ]
  [ 6.04267315  0.57131862  ] ...]
 
  # if using numpy (np) for matrix multiplication 
 # for cluster 0 ...
 
 big_gamma = np.sum(assignments[:, 0]
 mew = np.matmul(assignments[:, 0], features) / big_gamma
 
 # returns an array of mew
 [[-2.66780392  8.93576069]
  [-6.95170962 -6.67621669]
  [ 4.49951001  1.93892013]]

对于方差（𝜎），请考虑到现在，我们有了点和中心点-随着方差的出现，我们基本上正在评估每个样本的点（每个i的x）到每个群集的中心点（每个i的mew）的距离。用EM语言来说，有些人可能会说“ x_i减去mew_i乘以Big Gamma j。”

 # for figure 5 - variance
 # a sampling of variance for cluster 0 of n clusters
 # given arrays for features and assignments...
 
 x_i = features
 big_gamma = np.sum(assignments[:, 0]
 mew = np.matmul(assignments[:, 0], features) / big_gamma
 
 numerator = np.matmul(assignments[:, 0], (x_i - mew) ** 2)
 
 variance = numerator / big_gamma
 
 # returns an array of variance
 [[0.6422345  1.06006186]
  [0.65254746 0.9274831 ]
  [0.95031461 0.92519751]]

以上步骤都是关于EM中的M-Step或最大化-所有关于权值、mew和方差的都是关于优化的;但是，初始赋值数组呢?我们如何得到每个样本的概率数组这是EM中的E-Step，也就是期望。

在E-Step中，我们尝试用贝叶斯规则猜出每个点的分配-这会产生一组值，这些值指示每个点对高斯的响应度或概率。最初会与猜测值（后验值）相差很远，但是在通过E-Step和M-Step循环之后，这些猜测会变得更好，更接近客观的地面真理。

GMM算法重复M-Step 和 E-Step直到收敛。例如，收敛性可能是迭代的最大次数，或者当每轮猜测之间的差异变得非常小时。希望最终的结果是，数据中的每个样本都有一个软分配的标签。

总结

在这篇文章中，我介绍了M-Step的高斯混合模型算法的期望最大化阶段的导航部分的理解。虽然从表面上看，数学似乎太复杂而无法处理，但我们可以通过理解其各个部分来处理其复杂性。例如，一些关键的理解，如发音的希腊符号和应用它们的操作与NumPy是重要的，以掌握总体概念。

作者：Justin Chae

原文地址：https://towardsdatascience.com/unlock-m-step-from-em-in-gmm-dd9a32a0aa6f

deephub翻译组