众所周知,线特征比点特征可以提供更多的约束条件,并且在某些场合下比点特征要鲁棒。但是如果我们想要把线特征加入到SLAM系统中面临的是参数化和优化求导。这篇文章介绍了贺博的PL-VIO中线特征的参数化和求雅克比。
下面我们就来详细介绍一下空间直线的两种参数化方法:Plücker参数化方法,直线正交表示方法。为什么需要两种参数化方法呢?因为空间中的直线有4个自由度,而Plücker参数化方法需要使用6个参数表示直线,这样就会导致过参数化,过参数化在优化的时候就需要采用带约束的优化,不太方便。于是引入了可以用4个参数更新直线的正交表示来方便优化。这两种参数化方法可以很方便的相互转换,所以我们可以在SLAM系统中同时使用这两种参数化形式,在初始化和进行空间变换的时候使用Plücker坐标,在优化的时候使用正交表示。下面我们就来详细了解这两种参数化方法和优化的雅克比求导。
1. Plücker参数化方法
在3D空间中,直线的Plücker坐标表示为
,其中
是直线的方向向量,
是由直线和光心构成的平面
的法向量。Plücker坐标是过参数化的,比如
和
之间存在约束关系(
)。于是Plücker坐标不能直接使用无约束的优化。不过这种使用法向量和方向向量的表现形式在初始化直线和进行空间变换的时候很方便。所以在SLAM系统中我们可以使用Plücker坐标来初始化和变换,具体的初始化和变换方法如下。
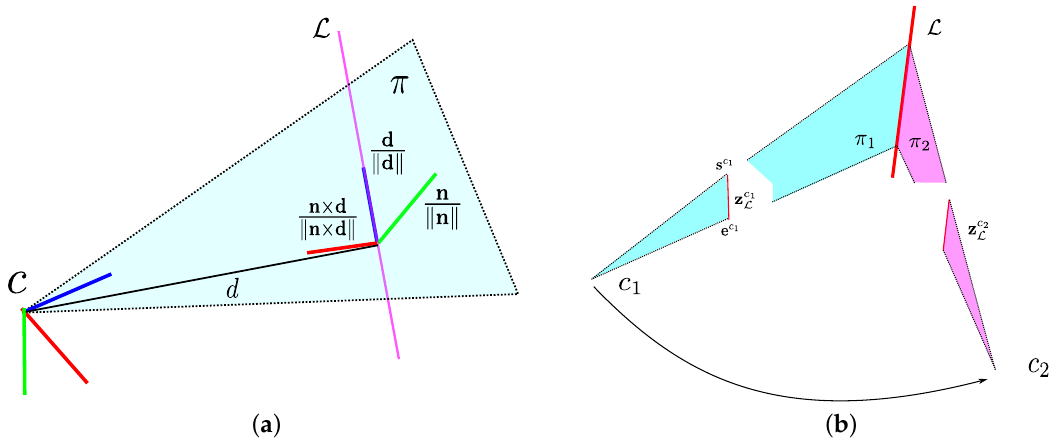
图1 线特征的Plücker坐标 (a)Plücker线坐标系 (b)新观测到的线的初始化
当给定从世界坐标系w到相机c的变换矩阵![T_{cw}=\left[\begin{matrix}{R_{cw}}&{{[p_{cw}]{\times}R{cw}}}\{0}&{R_{cw}}\\end{matrix}\right]](https://latex.csdn.net/eq?T_%7Bcw%7D%3D%5Cleft%5B%5Cbegin%7Bmatrix%7D%7BR_%7Bcw%7D%7D%26%7B%7B%5Bp_%7Bcw%7D%5D_%7B%5Ctimes%7DR_%7Bcw%7D%7D%7D%5C%5C%7B0%7D%26%7BR_%7Bcw%7D%7D%5C%5C%5Cend%7Bmatrix%7D%5Cright%5D),可以通过下面的形式将世界坐标系和相机坐标系下的Plücker线坐标进行变换:
当我们从不同的两帧相机观测到一个新的线路标的时候,Plücker坐标初始化方式也很简单。如图1b中所示,直线在两帧图像
和
中表示为两个线段
和
。线段
在归一化平面可以被两个端点表示,
和
。再加上坐标原点
,这三个点可以确定一个平面:
,使其满足
其中:
然后对同一个空间直线在两帧相机平面的投影和相机光心可以确定两个平面和
,通过两个平面可以确定唯一的空间直线。有了这两个平面我们可以得到对偶Plücker矩阵
然后从对偶矩阵中可以提取出Plücker坐标。法向量
和方向向量
都不要求是单位向量。
2. 正交表示法
由于3D空间的直线只有4个自由度,使用Plücker坐标这种过参数化的表示形式在优化的时候不方便,所以我们引入四个参数的正交表示。Plücker坐标和正交表示之间可以很方便的互相转换,我们之后会分别介绍如何从Plücker坐标到正交表示和正交表示怎么变换成Plücker坐标。首先我们需要知道了直线的Plücker坐标
,然后对
进行QR分解,得到:
分解得到的第一项是正交矩阵,是一个旋转矩阵。所表示的是相机坐标系到直线坐标系的旋转。其中直线坐标系的定义如下:用直线的方向向量以及直线和光心组成平面的法向量作为坐标的两个轴,再用他们叉乘得到的向量作为第三个轴,所以
其中代表的是相机坐标系到直线坐标系在x,y和z轴的旋转角。
到此我们得到了正交表示的第一项,第二项需要做一些小变换。由于将,结合之后只有一个自由度,所以我们可以用三角函数矩阵参数化:

上式中的是旋转角。由于坐标原点(相机光心)到3D直线的距离是
,所以 包含了距离信息d的。根据
和
的定义可以看出,4个自由度包括旋转的3个自由度和距离的一个自由度。在优化的时候,我们使用
作为空间直线更新的最小表示。
正交表示到Plücker坐标之间的变换可以通过下面的方式计算出来:
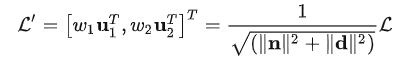
其中代表的是
矩阵的第i列。虽然
和
有一个尺度的差,但是它们表示的是同一条空间直线。
3. 直线的观测模型和误差

图2 空间直线投影到像素平面
要想知道线特征的观测模型,我们需要知道线特征从归一化平面到像素平面的投影内参矩阵。如图2,点C和D是直线
上两点,点c和d是它们在像素平面上的投影。
,
,K是相机的内参矩阵。
,
。那么有

上式表明,直线的线投影只和法向量有关和方向向量无关。

关于投影的误差,我们不可以直接从两幅图像的线段中得到,因为同一条直线在不同图像线段的长度和大小都是不一样的。衡量线的投影误差必须从空间中重投影回当前的图像中才能定义误差。在给定世界坐标系下的空间直线和正交表示
,我们首先使用
将直线变换到相机
坐标下。然后再将直线投影到成像平面上得到投影线段
,然后我们就得到了线的投影误差。我们将线的投影误差定义为图像中观测线段的端点到从空间重投影回像素平面的预测直线的距离。

其中和
是图像中观测到的线段端点,
是重投影的预测的直线。
4. 误差雅克比推导
如果要优化的话,需要知道误差的雅克比矩阵:
线特征在VIO下根据链式求导法则:

其中第一项,因为

所以:

第二项,因为
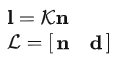
所以:
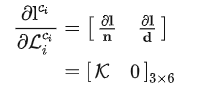
最后一项矩阵包含两个部分,一个是相机坐标系下线特征对的旋转和平移的误差导数,第二个是直线对正交表示的四个参数增量的导数
第一部分中,

在VIO中,如果要计算线特征的重投影误差,需要将在世界坐标系w下的线特征变换到IMU坐标系 b下,再用外参数变换到相机坐标系c下。所以

其中

线特征只优化状态变量中的位移和旋转,所以只需要对位移和旋转求导,其他都是零。下面我们来具体分析旋转和位移的求导。首先是线特征对旋转的求导:
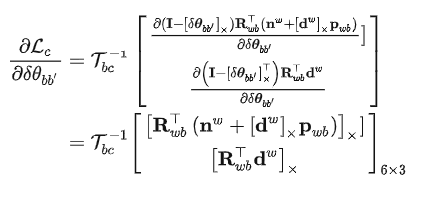
然后是线特征对位移的求导:

第二部分中,先解释第一个
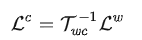
所以
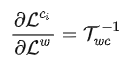
然后后面的有两种思路,先介绍第一种:

其中对
和
求导,因为
,所以


然后是对
和
对
的求导,

附录
Plücker坐标变换矩阵自洽性证明
此处把位姿矩阵写作T,其对应的Plücker坐标变换矩阵写作
如果,那么
是否成立呢?
证明如下
而
有定理,所以
证毕
参考文献
PL-VIO: Tightly-Coupled Monocular Visual–Inertial Odometry Using Point and Line Features
SLAM中线特征的参数化和求导 - 知乎
版权归原作者 瞻邈 所有, 如有侵权,请联系我们删除。