马修斯相关系数MCC简介

在评估机器学习模型的性能时，F1score都被首选指标。在本文中，我们将介绍一个值得更多关注和认可的替代度量:马修斯相关系数(MCC)。

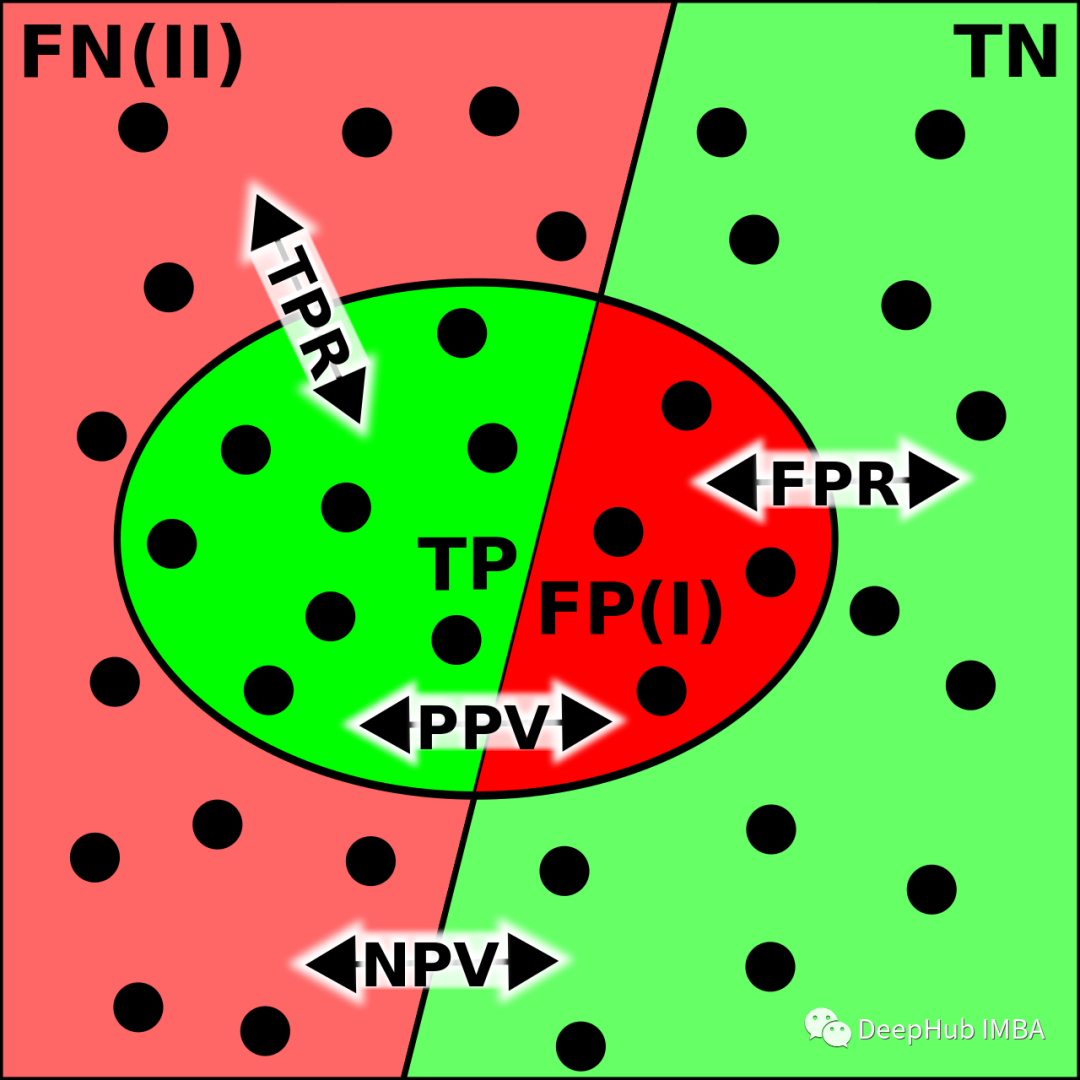
F1score通过协调准确率和召回率来计算，旨在在两者之间取得平衡。但是假设我们有一个具有以下混淆矩阵的数据集:

在这种情况下，数据集代表了一种罕见疾病的医学测试，只有少量正例。混淆矩阵表明该模型具有高的真反例（TN）率，但具有低的真正例（TP）率。以下是精确度、召回率和F1分数的计算结果：

F1的成绩在0.769左右，这似乎是一个合理的表现。但是少量遗漏的正例也可能对现实世界产生重大影响。

所以我们引入一个新的指标：马修斯相关系数（Matthews Correlation Coefficient，MCC）

马修斯相关系数MCC

马修斯相关系数 Matthews coefficient 是一种用于评估二元分类模型性能的指标，特别适用于处理不平衡数据集。它考虑了真正例（TP）、真反例（TN）、假正例（FP）和假反例（FN），提供一个能够总结分类质量的单一数值。

MCC的取值范围在-1到+1之间，其中：

MCC的计算公式为：

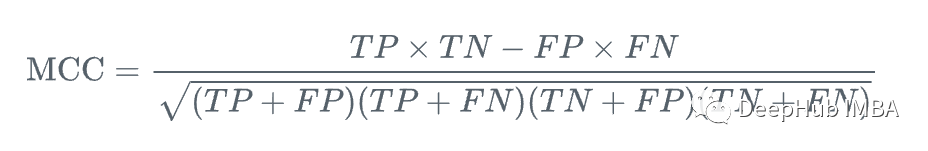
在这个公式中：

MCC考虑了所有四个值（TP、TN、FP、FN），因此适用于存在类别不平衡的数据集，其中一个类别可能比另一个类别更常见。特别是希望评估模型性能而不受类别分布影响时，MCC非常有用。

根据上面的例子，我们的MCC计算结果为：

 MCC = (25 * 9000 - 10 * 5) / sqrt((25 + 10) * (25 + 5) * (9000 + 10) * (9000 + 5))
 MCC ≈ 0.517

MCC值约为0.517。

在实践中，较高的MCC值表示更好的性能，+1 是理想的得分。通常情况下，大于0.5的值被认为是良好的，约为0的值表示随机性能。负值则暗示性能较差或模型比随机猜测还要差。

定义和计算方式：- MCC 是一个综合性能指标，考虑了真正例、真反例、假正例和假反例，通过一个复杂的公式计算得出。- F1 分数是精确率（Precision）和召回率（Recall）的调和平均值，表示了模型在平衡了预测的精确性和覆盖率后的表现。
权衡不平衡数据集：- MCC 可以在不平衡的数据集中提供更准确的性能评估，因为它同时考虑了四个分类结果，包括真反例和真正例。- F1 分数也考虑了不平衡数据集，但主要关注了模型的精确率和召回率之间的权衡。
优点和适用场景：- MCC 对于类别不平衡的情况和样本量较小的情况下更有优势，因为它在评估性能时考虑了所有四个分类结果，减少了结果的随机性。- F1 分数在关注模型能够正确识别正例的情况下也保持较好的表现，适用于一些需要平衡精确率和召回率的场景。
解释性：- MCC 的取值范围在-1到+1之间，更容易解释。+1 表示完美预测，-1 表示完全不一致，0 表示随机。- F1 分数的取值范围在0到1之间，也很容易解释。1 表示完美的精确率和召回率平衡。

马修斯相关系数（Matthews Correlation Coefficient，MCC）和 F1 分数（F1 Score）都是用于评估二元分类模型性能的指标，但它们从不同的角度考虑了模型的预测结果。

如果数据集存在严重的类别不平衡，并且想要一个更全面的性能评估指标，那么 MCC 可能更合适。如果只关心模型的精确率和召回率的平衡，而不太关心真反例和真正例的比例，那么 F1 分数可能更适合。

标签：机器学习