python实现汉诺塔问题

汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞n片黄金圆盘。大梵天命令婆罗门把圆盘从下自上开始、按大小顺序重新摆放在另一根柱子上。并且规定，小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘，如图所示。问应该怎样移动，才能将圆盘移动到另一根柱子上。

将n设为1、2、3三种情况进行讨论，来介绍汉诺塔问题。将三根柱子分别标记为A、B、C。
（1）当n=1时，直接将红色圆盘从A柱上移动到C柱上，移动过程示意图如图所示。

（2）当n=2时，也就是把A柱上2层圆盘移动到C柱上，步骤如下：
步骤1：将A柱上的黄色圆盘移动到B柱上，移动过程示意图如图所示。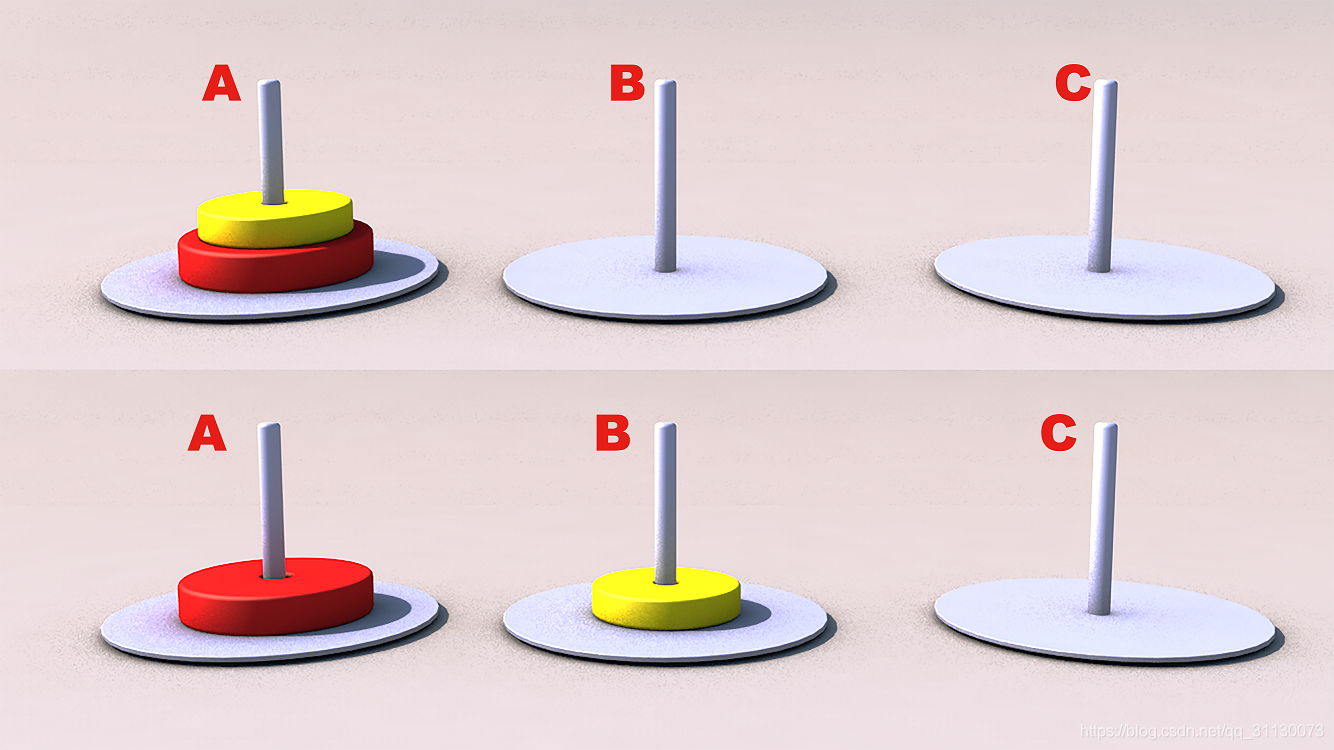

步骤2：将A柱上的红色圆盘移动到C柱上，移动过程示意图如图所示。

步骤3：将B柱上的黄色圆盘移动到C柱上，移动过程示意图如图所示。

（3）当n=3时，也就是先将A柱上的红、黄、绿三个圆盘移动到C柱子上，移动过程示意图如图所示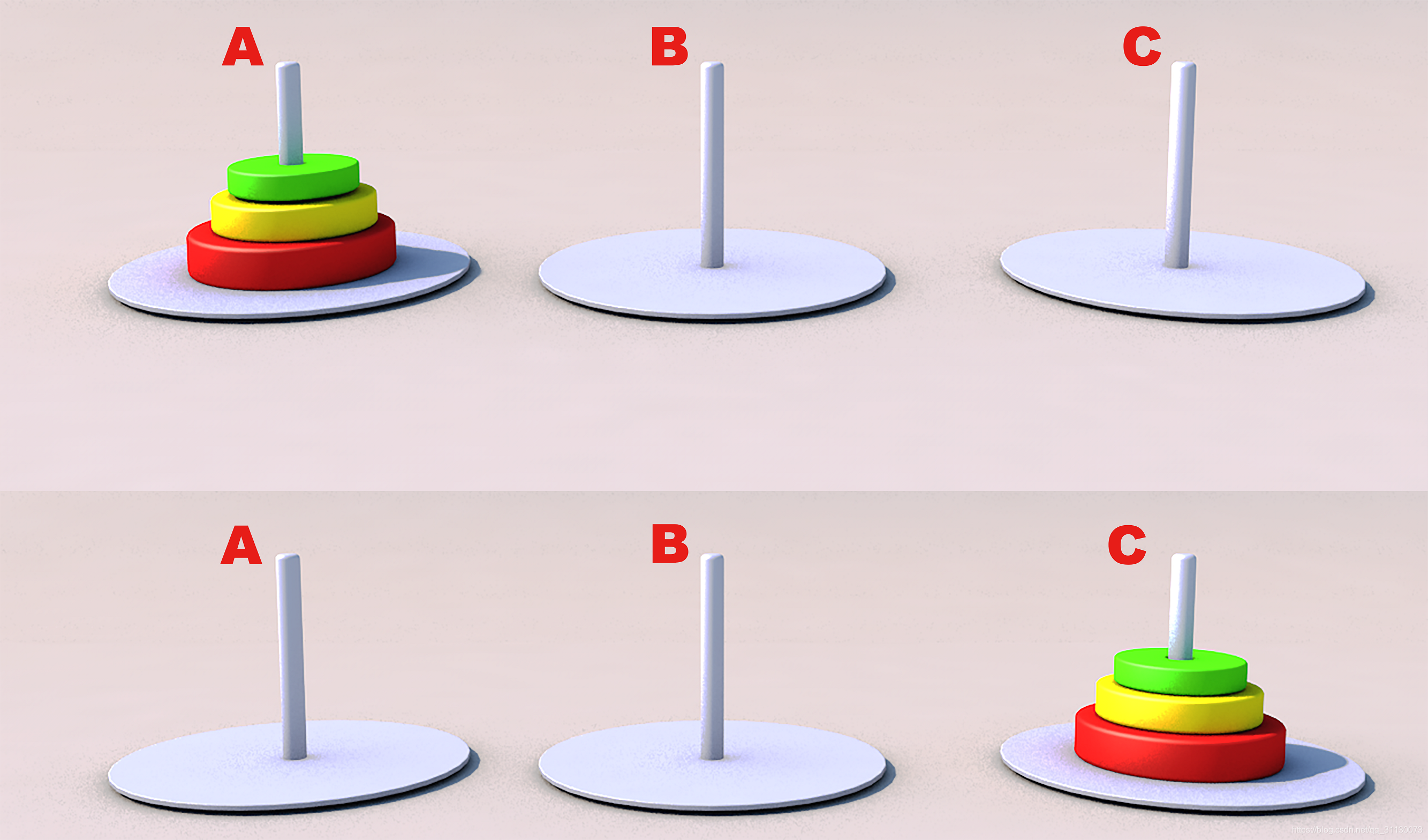

步骤1：将A柱上的绿色圆盘移动到C柱上，移动过程示意图如图所示。

步骤2：将A柱上的黄色圆盘移动到B柱上，移动过程示意图如图所示。

步骤3：将C柱上的绿色圆盘移动到B柱的黄色圆盘上，移动过程示意图如图所示。

步骤4：将A柱上的红色圆盘移动到C柱上，移动过程示意图如图所示。

步骤5：将B柱上的绿色圆盘移动到A柱上，移动过程示意图如图所示。

步骤6：将B柱上的黄色圆盘移动到C柱上，移动过程示意图如图所示。

步骤7：将A柱上的绿色圆盘移动到C柱上，移动过程示意图如图所示。

这就是将3层圆盘按照规定移动到另一根柱上的整个过程。不论是3层还是4层还是n层，移动的算法都是这样的，首先是将A柱最上方的n-1个圆盘落在B柱，将此时A柱的最小圆盘落在C柱，B柱上的n-1个圆盘，落在C柱。
python代码实现汉诺塔问题如下：

defhanoi(n,A,B,C):#定义汉诺塔函数,参数n是圆盘数，A、B、C是3根柱if n==1:#判断圆盘数，如果等于1，递归条件print(A,'-->',C,' ',n)# 直接将A柱上的圆盘移动到C柱上else:#否则，进行递归移动
      hanoi(n-1,A,C,B)#递归将A柱最上方的n-1个盘子落在B柱print(A,'-->',C,' ',n)# 输出将A柱上的圆盘移动到C柱上,也就是将A柱的最小面盘子落在C柱
      hanoi(n-1,B,A,C)#递归将B柱上的n-1个盘子，落在C柱

hanoi(3,'A','B','C')#调用函数

汉诺塔问题移动的算法如下（n表示圆盘个数）：
 n=1时，移动次数为21-1
 n=2时，移动次数为22-1
 n=3时，移动次数为23-1
 n=4时，移动次数为：24-1
 n=5时，移动次数为：25-1
得出结论：A柱有n个圆盘时，移动次数为2n-1。

本文章是博主自创，如转载，请附上链接