0
0

【初阶与进阶C++详解】第十七篇：红黑树（插入+验证+查找）

🏆个人主页：企鹅不叫的博客

​ 🌈专栏

  • C语言初阶和进阶
  • C项目
  • Leetcode刷题
  • 初阶数据结构与算法
  • C++初阶和进阶
  • 《深入理解计算机操作系统》
  • 《高质量C/C++编程》
  • Linux

⭐️ 博主码云gitee链接：代码仓库地址

⚡若有帮助可以【关注+点赞+收藏】，大家一起进步！

💙系列文章💙

【初阶与进阶C++详解】第一篇：C++入门知识必备

【初阶与进阶C++详解】第二篇：C&&C++互相调用（创建静态库）并保护加密源文件

【初阶与进阶C++详解】第三篇：类和对象上（类和this指针）

【初阶与进阶C++详解】第四篇：类和对象中（类的六个默认成员函数）

【初阶与进阶C++详解】第五篇：类和对象下（构造+static+友元+内部类

【初阶与进阶C++详解】第六篇：C&C++内存管理（动态内存分布+内存管理+new&delete）

【初阶与进阶C++详解】第七篇：模板初阶（泛型编程+函数模板+类模板+模板特化+模板分离编译）

【初阶与进阶C++详解】第八篇：string类（标准库string类+string类模拟实现）

【初阶与进阶C++详解】第九篇：vector(vector接口介绍+vector模拟实现+vector迭代器区间构造/拷贝构造/赋值)

【初阶与进阶C++详解】第十篇：list(list接口介绍和使用+list模拟实现+反向迭代器和迭代器适配)

【初阶与进阶C++详解】第十一篇：stack+queue+priority_queue+deque（仿函数）

【初阶与进阶C++详解】第十二篇：模板进阶(函数模板特化+类模板特化+模板分离编译)

【初阶与进阶C++详解】第十三篇：继承(菱形继承+菱形虚拟继承+组合)

【初阶与进阶C++详解】第十四篇：多态（虚函数+重写（覆盖）+抽象类+单继承和多继承）

【初阶与进阶C++详解】第十五篇：二叉树搜索树（操作+实现+应用KVL+性能+习题）

【初阶与进阶C++详解】第十六篇：AVL树-平衡搜索二叉树（定义+插入+旋转+验证）

文章目录

💎一、红黑树概念和性质

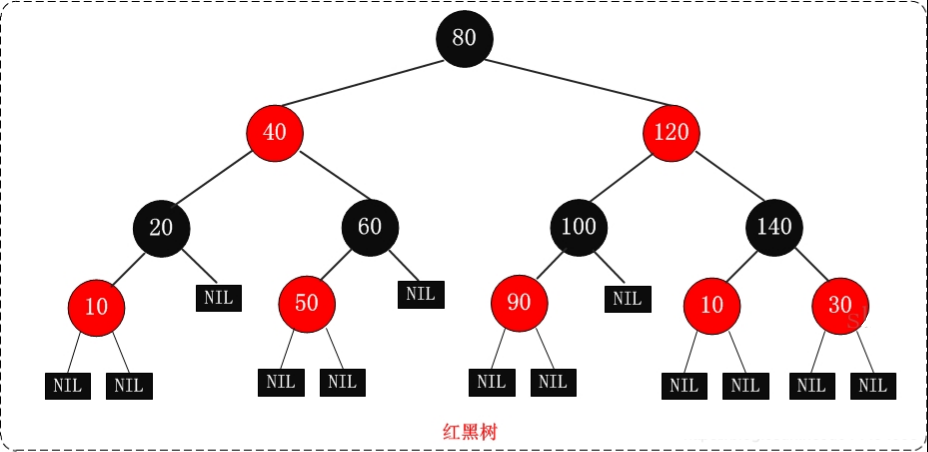
红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。它是通过控制节点颜色的方式来控制这棵树的相对平衡，最长路径的小于最短路径的2倍，这使得红黑树在最坏的情况下，也能有

O(logN)

的查找效率，最短路径是全黑，最长路径是一黑一红。

image-20220904165644609

红黑树的性质：

1.结点是红色或黑色。
2.根结点是黑色。
3.所有叶子都是黑色。（叶子是空结点）
4.每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）
5.从任一节结点到其每个叶子的所有路径都包含相同数目的黑色结点
上面的五个性质还可以用更通俗的语言描述为三句话：

1.根节点是黑色的
2.没有连续的红节点
3.每条路径的黑节点数目相同（每条路径指的是从根节点到黑色的空节点）,一条路径上红色节点的数量一定不会超过黑色节点的数量

💎二、红黑树节点定义

本质一样是二叉搜索树，和AVL树不同的是，增加了颜色的定义

//枚举，定义颜色enumColor{
    RED,//0
    BLACK,//1};//节点类template<classK,classV>structRBTreeNode{
    RBTreeNode<K, V>* _left;
    RBTreeNode<K, V>* _right;
    RBTreeNode<K, V>* _parent;
    pair<K, V> _kv;
    Color _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED)//默认设置为红色，因为这个满足性质3且不会破坏性质4{}};

💎三、红黑树结构

template<classK,classV>classRBTree{typedef RBTreeNode<K, V> Node;public:private:
    Node* _root =nullptr;};

💎四、红黑树插入（重要）

🏆1.寻找插入的位置

若key值大于当前结点的key值，则向右寻找；若小于，则向左寻找；若相等，说明数据冗余，返回false。

🏆2.判断是否符合红黑树规则

插入的新节点默认是红色，同时要符合条路径上黑色结点数量相等这条规则，故判断是否为红黑树就转换为判断是否存在连续红色的结点，对于新插入的结点，若其父亲颜色为黑色，则满足红黑树的规则，无需调整，而若其父亲颜色为红色，则规则被破坏，需要调整。

插入节点应为什么是默认成红色？如果是黑色呢？

如果选择插入黑结点，那1条路径上就多了1个黑结点，破坏了性质5(从任一节结点到其每个叶子的所有路径都包含相同数目的黑色结点)，代价很大。插入红结点，如果它的父亲结点是黑色则不用调整，它的父亲是红色那我们在进行后序的处理。

总结一下，其实无论选红还是黑，后续都要再处理，但是处理的代价不一样：
1.插入黑色结点一定破坏性质5，调整起来会很麻烦
2.插入红结点不一定破坏红黑树的性质，它的父亲结点是红色才进行调整，比插入黑结点调整起来方便。

🏆3.破坏红黑树规则，调整节点颜色

以下用p来代表parent结点，cur代表cur为新增结点,g代表grandparent结点，u代表uncle结点。

1.1如果插入节点的父亲是黑色节点，那么可以直接结束，不需要继续调整了

1.2如果插入节点为的父亲为红色节点

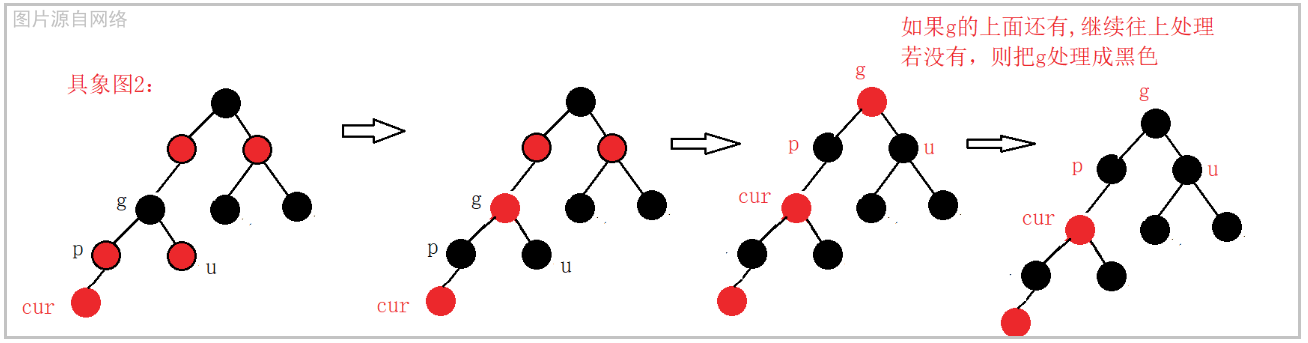
情况一：cur为红， p为红， g为黑， u存在且为红

解决方法：此时只需变色，将parent和uncle变为黑色，grandparent变为红色，同时，因为祖父之上可能还有其他节点，还需要从祖父g的位置继续向上调节。

image-20220904171321583

情况二：cur在p的左边，p为红，g为黑，u存在为黑色/u不存在 （孩子，父亲，祖父呈直线状态）-单旋

分析处理：

  1. 如果叔叔存在，则此时的孩子节点可能是下面的子树在进行变色处理时，将其从原本的黑色变为了红色。（否则不满足路径黑节点数量相同的性质），如果父亲是祖父的左孩子，孩子是父亲的左孩子，此时祖父进行右单旋
  2. 如果叔叔不存在，则此时的孩子节点是刚插入进来的结点，因为不能有连续的红结点，所以孩子和父亲必须有一个是黑色，但是此时又不满足黑节点数量相同的性质，如果父亲是祖父的右孩子，孩子是父亲的右孩子，此时祖父进行左单旋。
  3. 旋转完后，p变为黑色，g变为红色

在这里插入图片描述
情况三：cur在p的右边，p为红，g为黑，u存在为黑色/u不存在 (孩子，父亲，祖父呈折线状态)-双旋

分析处理：

  1. 如果父亲是祖父的左孩子，孩子是父亲的右孩子，父亲此时进行左单旋，孩子再进行右单旋。
  2. 如果父亲是祖父的右孩子，孩子是父亲的左孩子，父亲此时进行右单旋，孩子再进行左单旋。
  3. 双旋之后，cur变为黑色，p和g为红色。在这里插入图片描述 旋转代码如下：
voidRotateL(Node* parent){
        Node* subR = parent->_right;
        Node* subRL = subR->_left;// 1.先让把subR的左边（可能为空也可能不为空）作为parent的右边
        parent->_right = subRL;// 2.如果subRL不为空，就让subRL的父指针指向parentif(subRL)
            subRL->_parent = parent;// 3.先记录parent的父节点的位置，然后把parent作为subR的左边 
        Node* ppNode = parent->_parent;
        subR->_left = parent;// 4.parent的父指针指向subR
        parent->_parent = subR;// 5.如果ppNode为空==>说明subR现在是根节点，就让subR的父指针指向nullptr//不是根节点就把subR的父指针指向parent的父节点，parent的父节点（左或右）指向subRif(parent == _root){// 更新根节点
            _root = subR;
            _root->_parent =nullptr;}else{// 判断parent是ppNode的左还是右if(parent == ppNode->_left){
                ppNode->_left = subR;}else{
                ppNode->_right = subR;}

            subR->_parent = ppNode;}// 6.把parent和subR的平衡因子更新为0
        subR->_bf = parent->_bf =0;}voidRotateR(Node* parent){//让不平衡的结点parent的左子树变为其原本左子树subL的右节点subLR
    Node* subL = parent->_left;
    Node* subLR = subL->_right;// 1.先让把subL的右边（可能为空也可能不为空）作为parent的左边
    parent->_left = subLR;// 2.如果subLR存在，就让subLR的父指针指向parentif(subLR)
        subLR->_parent = parent;// 3.先记录parent的父节点的位置，然后把parent作为subL的右边
    Node* ppNode = parent->_parent;
    subL->_right = parent;// 4.parent的父指针指向subL
    parent->_parent = subL;// 5.如果parent为根节点，则让subL成为新的根节点if(parent == _root){// 更新根节点
        _root = subL;
        _root->_parent =nullptr;}//如果不是根节点，则改变subL与其祖父节点的指向关系else{// 判断parent是ppNode的左还是右if(ppNode->_left == parent){
            ppNode->_left = subL;}else{
            ppNode->_right = subL;}
        subL->_parent = ppNode;}// 6.把parent和subL的平衡因子更新为0
    subL->_bf = parent->_bf =0;}

插入代码如下：

boolInsert(const pair<K, V>& kv){// 1、搜索树的规则插入// 2、看是否违反平衡规则，如果违反就需要处理：旋转按照二叉搜索树的规则先找到位置if(_root ==nullptr){
    _root =newNode(kv);
    _root->_col = BLACK;returntrue;}

  Node* parent =nullptr;
  Node* cur = _root;while(cur){if(cur->_kv.first < kv.first){
      parent = cur;
      cur = cur->_right;}elseif(cur->_kv.first > kv.first){
      parent = cur;
      cur = cur->_left;}else{returnfalse;}}

  cur =newNode(kv);
  cur->_col = RED;//判断插入位置if(parent->_kv.first < kv.first){
    parent->_right = cur;}else{
    parent->_left = cur;}

  cur->_parent = parent;//更新红黑树，如果父节点的颜色为黑，则说明满足条件，不需要处理，如果为红，则说明不满足，需要处理。while(parent && parent->_col == RED){
    Node* grandfater = parent->_parent;assert(grandfater);//如果父节点为祖父的左子树if(grandfater->_left == parent){此时判断叔叔节点的状态，红黑树状态取决于叔叔
      Node* uncle = grandfater->_right;// 情况一：如果叔叔节点存在且为红，则直接把父亲和叔叔变黑，祖父节点边红即可。然后再从祖父的位置继续往上调整if(uncle && uncle->_col == RED){// 变色
        parent->_col = uncle->_col = BLACK;
        grandfater->_col = RED;// 继续往上处理
        cur = grandfater;
        parent = cur->_parent;}/*
                叔叔节点为黑或者不存在，此时有两种情况
                情况二：cur为父节点的左子树，即直线状态， 右单旋，改p和g颜色。
                情况三：cur为父节点的右子树，即折线状态，左单旋回到情况二。
      */else{if(cur == parent->_left)// 右单旋{//     g//   p// cRotateR(grandfater);
          parent->_col = BLACK;
          grandfater->_col = RED;}else// 双旋-左右{//     g//   p//     c RotateL(parent);RotateR(grandfater);
          cur->_col = BLACK;
          grandfater->_col = RED;}break;}}//父亲在右边，叔叔在左边else{
      Node* uncle = grandfater->_left;// 情况一：如果叔叔节点存在且为红，则直接把父亲和叔叔变黑，祖父节点边红即可。然后再从祖父的位置继续往上调整if(uncle && uncle->_col == RED){// 变色
        parent->_col = uncle->_col = BLACK;
        grandfater->_col = RED;// 继续往上处理
        cur = grandfater;
        parent = cur->_parent;}/*
                叔叔节点为黑或者不存在，此时有两种情况
                情况二：cur为父节点的左子树，即直线状态， 左单旋，改p和g颜色。
                情况三：cur为父节点的右子树，即折线状态，右单旋回到情况二。
      */else{if(cur == parent->_right)//左单旋{// g//   p//     c RotateL(grandfater);
          parent->_col = BLACK;
          grandfater->_col = RED;}else// 双旋-右左{// g//   p// cRotateR(parent);RotateL(grandfater);
          cur->_col = BLACK;
          grandfater->_col = RED;}break;}}}//强制转换把根变成黑
  _root->_col = BLACK;returntrue;}

💎五、红黑树验证

🏆1.计算最小最大高度判断

两者区别，把大于号改成小于号，返回小的那个子树的高度+1。只要最大长度小于最小长度的2倍，那么基本规则就是没有破坏的

//最大长度int_maxHeight(Node* root){if(root ==nullptr)return0;int lh =_maxHeight(root->_left);int rh =_maxHeight(root->_right);return lh > rh ? lh +1: rh +1;}//最小长度int_minHeight(Node* root){if(root ==nullptr)return0;int lh =_minHeight(root->_left);int rh =_minHeight(root->_right);return lh < rh ? lh +1: rh +1;}

🏆2.通过检查红黑树性质判断

  1. 根节点一定是黑色
  2. 不存在连续的红节点
  3. 每一个到叶子（空节点NIL）的支路上黑节点数量相同
boolIsBalanceTree(){// 检查红黑树几条规则
  Node* pRoot = _root;// 空树也是红黑树if(nullptr== pRoot)returntrue;// 检测根节点是否满足情况1，根节点是黑色if(BLACK != pRoot->_col){
    cout <<"违反红黑树性质一：根节点必须为黑色"<< endl;returnfalse;}// 获取任意一条路径中黑色节点的个数，作为基准值
  size_t blackCount =0;
  Node* pCur = pRoot;while(pCur){if(BLACK == pCur->_col)
      blackCount++;

    pCur = pCur->_left;}// 检测是否满足红黑树的性质，k用来记录路径中黑色节点的个数
  size_t k =0;return_IsValidRBTree(pRoot, k, blackCount);}//检测是否为RB树bool_IsValidRBTree(Node* pRoot, size_t k,const size_t blackCount){//先计算一条路径的黑色结点数量，然后遍历其他各条路径，对比黑色结点的数量，若不相等，则返回false。// 走到空就判断该条路径的黑节点是否等于blackCountif(nullptr== pRoot){if(k != blackCount){
      cout <<"违反性质三：每条路径中黑色节点的个数必须相同"<< endl;returnfalse;}returntrue;}// 统计黑色节点的个数if(BLACK == pRoot->_col)
    k++;// 检测当前节点与其双亲是否都为红色//判断红色结点的父亲是否为红色，这样就可以简化代码及操作if(RED == pRoot->_col && pRoot->_parent && pRoot->_parent->_col == RED){
    cout <<"违反性质二：存在连在一起的红色节点"<< endl;returnfalse;}return_IsValidRBTree(pRoot->_left, k, blackCount)&&_IsValidRBTree(pRoot->_right, k, blackCount);}

💎六、红黑树查找

和二叉搜索树一样

//因为kvl树我们需要修改value，所以返回节点的指针
    Node*_FindR(Node* root,const K& key){if(root ==nullptr)returnnullptr;if(root->_kv.first < key){return_FindR(root->_right, key);}elseif(root->_kv.first > key){return_FindR(root->_left, key);}else{return root;}}//查找是通过key来进行的
    Node*FindR(const K& key){return_FindR(_root, key);}

💎七、红黑树与AVL树比较

  • AVL树是严格平衡的，而红黑树是近似平衡的
  • AVL树和红黑树的查找时间复杂度都是O(logN)
  • 由于红黑树旋转次数更少，因此在增删过程中性能较优，AVL更适合查找数据

💎八、红黑树应用

最为经典的便是map和set这两个容器，它们便使用了红黑树作为底层逻辑

标签： c++ java 算法
本文转载自: https://blog.csdn.net/YQ20210216/article/details/127113230
版权归原作者 企鹅不叫 所有， 如有侵权，请联系我们删除。
登录后发布评论

“【初阶与进阶C++详解】第十七篇：红黑树（插入+验证+查找）”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

【Python】【持续项目】Python-安全项目搜集

泷羽sec学习day5-安全见闻6

随身 WiFi 通过 USB 连接路由器共享网络 扩展网络覆盖范围

如何将 Kubernetes 中的两个 Nginx Ingress 合并成一个：操作步骤与注意事项

单元测试使用JUnit 5

【大数据学习 | HBASE高级】hive操作hbase

MySQL Workbench 8.0 CE 中文汉化教程

文章导航