强化学习PPO从理论到代码详解(1)--- 策略梯度Policy gradient

第0章闲聊吹水

Proximal Policy Optimization(PPO) 近端策略优化，可以说是目前最稳定，最强的强化学习算法之一了，也是openAI默认的强化学习算法，有多叼不用我说了吧。

笔者在强化学习的道路上看来很多书，看了很多代码，和很多大佬的博客，只是很多都是侧重一个方面，所以我在吸取百家之长后，决定完完整整的写一回PPO从算法理论到逐行代码手敲和详解的文章，我会做到非常详尽，尽量做到每一个符号都解释。我在学习强化学的初期，入手了一些不那么友好的书籍或者视频，满脑都是：这个符号是啥？这个符号又是啥？😵😵😵后来我看来很多家的视频和书籍，主要参考了的easy RL 和李宏毅老师视频，当然还有很多大佬的博客我就不一一列出了。

我希望我的文章能给强化学习道路上的同志们一点帮助，由于笔者才疏学浅，有写的不好的地方还望大家多多指正批评，在此谢过👊。

本系列将分四章：

PPO基础之策略梯度(Policy gradient) 篇
PPO 算法详解篇
PPO 代码详写详解篇
PPO 实战篇

接下来就正式开始吧。

第一章策略梯度(Policy gradient)

基础概念

强化学习有三要素 1. 演员actor 2. 环境env 3.奖励函数 reward function

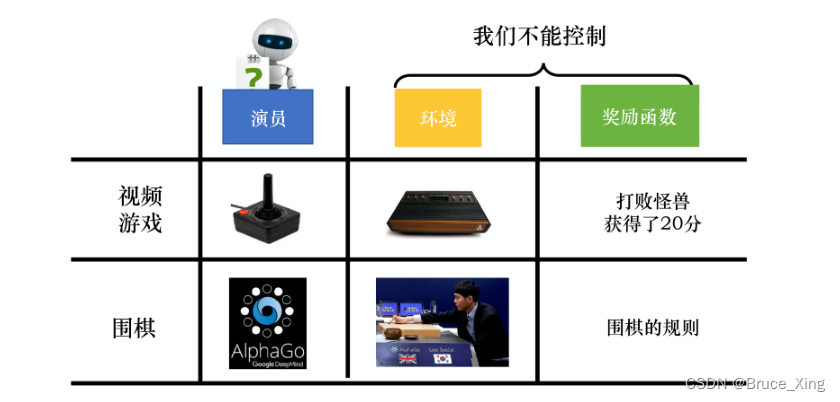
这个图就很好的阐述了这三个要素在实际应用当中的是什么，也很好理解。我们强化学习的目是什么呢？，就是训练出一个actor，这个actor玩游戏跟开了挂一样, 或者是下棋能击败人类一切玩家的棋神。这里我们把这个actor，或者说策略用 $\pi _{\theta (s)}$ 来表示，我们把这个

策略记做 $\pi$
$\theta$ 表示这个策略的参数，通常会用一个神经网络代替这个策略, $\theta$ 就是这个神经网络的参数
s表示这个策略网络的输入，也就是状态state, 或者说是observation，这个之后还会提到。

找到奖励

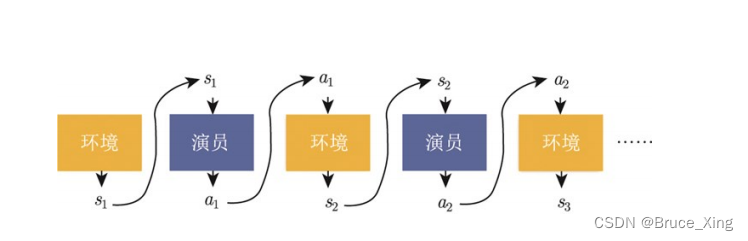
那么我们现在有个这个策略，我们就可以让这个策略去玩游戏，去和游戏环境做互动。像这样子

（这里不对马尔科夫过程做详细解释，不影响后面的理解）然后我们可以得到一条轨迹，这个轨迹长这个子。

                                         ![s_{1} ,a_{1} ,r_{1} ,s_{2} ,a_{2} ,r_{2} ... a_{t},r_{t}](https://latex.csdn.net/eq?%5Cdpi%7B150%7D%20s_%7B1%7D%20%2Ca_%7B1%7D%20%2Cr_%7B1%7D%20%2Cs_%7B2%7D%20%2Ca_%7B2%7D%20%2Cr_%7B2%7D%20...%20a_%7Bt%7D%2Cr_%7Bt%7D)                                   ** 1.1**

假设策略 $\pi _{\theta (s)}$ 是一个玩游戏AI，输入一个游戏状态s1, 策略网络根据这个游戏画面，选择一个动作a1，然后得到奖励r1，随着游戏画面改变，输入新游戏状态s2,选择下一个动作a2，得到奖励r2，依次循环直到游戏结束，直观上这还是很符合逻辑的嘛。

然后根据这个轨们迹我就可以的到一个总奖励，我们先把这个总奖励记做 $R{_{\theta }}$ ，根据上面1.1式中的轨迹来看，总奖励 $R_{\theta } = {\textstyle \sum_{t=1}^{T}} r_{t}$ ，这也很简单吧。但是事情到这里开始变复杂了，如果我们的奖励函数合理，又能很轻松得到 $R{_{\theta }}$ ，我们就优化网络让其最大化奖励不久完了吗，好，讲到这，完结撒花🌹🌹🌹。

当然，事情远没有结束，事实上，无论是在actor中，还是在环境中，随机性（randomness）都是不可避免的，同样的情况可能有不同的奖励。既然得不到完全准确 $R{_{\theta }}$ ，我们可以用一个期望值来代替，这个期望值记做 $\bar{R}{_{\theta }}$ ，现在问题是如何到底这个期望值 $\bar{R}{_{\theta }}$ ？

actor和环境互动，每玩一轮游戏，或者说每一个episode都可以得到一条轨迹 $\tau$ ，每条轨迹的reward也可以计算。

                          ![\tau = \left \{ s_{1} ,a_{1} ,r_{1} ,s_{2} ,a_{2} ,r_{2} ... a_{t},r_{t} \right \}](https://latex.csdn.net/eq?%5Cdpi%7B150%7D%20%5Ctau%20%3D%20%5Cleft%20%5C%7B%20s_%7B1%7D%20%2Ca_%7B1%7D%20%2Cr_%7B1%7D%20%2Cs_%7B2%7D%20%2Ca_%7B2%7D%20%2Cr_%7B2%7D%20...%20a_%7Bt%7D%2Cr_%7Bt%7D%20%5Cright%20%5C%7D)                            **1.2**

                          ![R_{(\tau)}=\sum_{n=1}^{N}r_{_{n}}](https://latex.csdn.net/eq?%5Cdpi%7B150%7D%20R_%7B%28%5Ctau%29%7D%3D%5Csum_%7Bn%3D1%7D%5E%7BN%7Dr_%7B_%7Bn%7D%7D)                                                                      **1.3**

每一个轨迹都一个概率（probability）, 这依赖于actor的参数 $\theta$ ，定义为 $P_{_{(\tau\mid \theta)}}$ 。如果我们能穷举所有的轨迹和对应的概率，那么 $\bar{R}{_{\theta }}$ 就会非常简单，公式如下。

                                                  ![\bar{R}{_{\theta }} = \sum_{ \tau}^{} R_{(\tau) } P_{(\tau \mid \theta) }](https://latex.csdn.net/eq?%5Cdpi%7B150%7D%20%5Cbar%7BR%7D%7B_%7B%5Ctheta%20%7D%7D%20%3D%20%5Csum_%7B%20%5Ctau%7D%5E%7B%7D%20R_%7B%28%5Ctau%29%20%7D%20P_%7B%28%5Ctau%20%5Cmid%20%5Ctheta%29%20%7D)                                        **1.4**

但是，but again，但是实际上得到所有的 $\tau$ 基本不可能，那怎么办呢？那么我们可以做sample, 只要sample的次数足够做， $\bar{R}{_{\theta }}$ 就能非常接近真实值（概率论的知识）。

现在让策略 $\pi _{\theta}$ 玩N次游戏，做很多次的采样。就可以获得很多条轨迹 $\left \{ \tau^{_{1}},\tau^{_{2}},\tau^{_{3}},\tau^{_{4}} ... \tau^{_{n}} \right \}$ 。

那现在公式变为了如下，

                                   ![\bar{R}{_{\theta }} = \sum_{ \tau}^{} R_{(\tau) } P_{(\tau \mid \theta) }\approx \frac{1}{N}\sum_{n=1}^{N}R_{\tau^{n}}](https://latex.csdn.net/eq?%5Cdpi%7B150%7D%20%5Cbar%7BR%7D%7B_%7B%5Ctheta%20%7D%7D%20%3D%20%5Csum_%7B%20%5Ctau%7D%5E%7B%7D%20R_%7B%28%5Ctau%29%20%7D%20P_%7B%28%5Ctau%20%5Cmid%20%5Ctheta%29%20%7D%5Capprox%20%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bn%3D1%7D%5E%7BN%7DR_%7B%5Ctau%5E%7Bn%7D%7D)                       **1.5        **

其实也很好理解，理想状态得到所有轨迹，各个轨迹概率和对应的这个奖励相乘就得到期望奖励值，现在做采样得到很多条轨迹求他们的平均奖励值，就可以近似得到期望奖励。

举个例子，如果我们掷一枚硬币，正面奖励为1，反面奖励为0，每一轮游戏扔10次，得到所有状态太麻烦，或者就认定其不可取，这时候我们干脆玩100轮，将所有的奖励求和，然后在求平均，得到这个奖励的期望值（应当是约等于5）。

梯度上升Gradient Ascent：

我先贴出求目标函数梯度的完整数学推导过程：

完了，BBQ了，估计到这你已经完成强化学习的从入门到放弃了。不过不要慌先忘记这一大串这个式子，一步一步来。

先从式1.4，我们知道了怎么求每个奖励的期望值。

                                                    ![\bar{R}{_{\theta }} = \sum_{ \tau}^{} R_{(\tau) } P_{(\tau \mid \theta) }](https://latex.csdn.net/eq?%5Cdpi%7B150%7D%20%5Cbar%7BR%7D%7B_%7B%5Ctheta%20%7D%7D%20%3D%20%5Csum_%7B%20%5Ctau%7D%5E%7B%7D%20R_%7B%28%5Ctau%29%20%7D%20P_%7B%28%5Ctau%20%5Cmid%20%5Ctheta%29%20%7D)

$\bar{R}{_{\theta }}$ 就可以看做是我们的目标方程（objective function）,我们要找的就是一组最优的参数 $\theta^{*}$ ，这个参数可以最大化 $\bar{R}{_{\theta }}$ .

                                                      ![\theta^{*} = argmax\bar{R}_{\theta}](https://latex.csdn.net/eq?%5Cdpi%7B150%7D%20%5Ctheta%5E%7B*%7D%20%3D%20argmax%5Cbar%7BR%7D_%7B%5Ctheta%7D)

既然要最大化 $\bar{R}{_{\theta }}$ ，就可以用gradient ascent! 其计算原理如下，有机器学习基础应当不难理解：

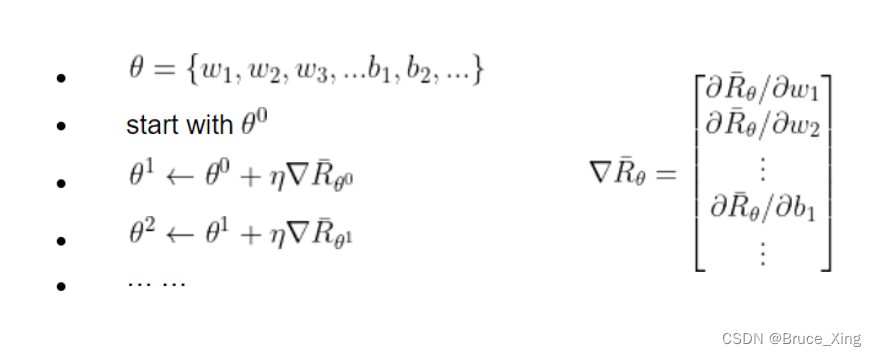
知道了思路，接下来对式1.4进行计算梯度计算，在贴一遍式1.4，防止忘记：

                                                         **![\bar{R}{_{\theta }} = \sum_{ \tau}^{} R_{(\tau) } P_{(\tau \mid \theta) }](https://latex.csdn.net/eq?%5Cdpi%7B150%7D%20%5Cbar%7BR%7D%7B_%7B%5Ctheta%20%7D%7D%20%3D%20%5Csum_%7B%20%5Ctau%7D%5E%7B%7D%20R_%7B%28%5Ctau%29%20%7D%20P_%7B%28%5Ctau%20%5Cmid%20%5Ctheta%29%20%7D)**

对 $\theta$ 求梯度过程如下，中间有一步很跳跃，主要用到了链式法则，链式法则我贴在右边。

注意看下面红色框，是不是感觉很熟悉。对，就是式1.5，把理想状态换成采样，我也把式1.5 贴在了红色框上面！

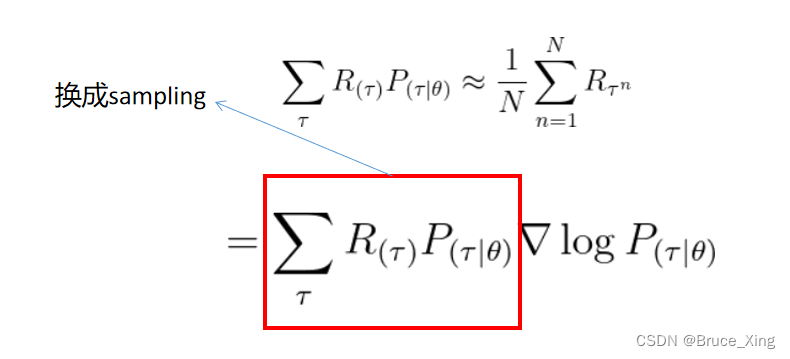
用式1.5替换之后，式子就变成了1.6。

                                           ![\bar{R}{_{\theta }} \approx \frac{1}{N}\sum_{n=1}^{N}R_{\tau^{n}} \nabla log P_{(\tau^{n}\mid\theta) }](https://latex.csdn.net/eq?%5Cdpi%7B150%7D%20%5Cbar%7BR%7D%7B_%7B%5Ctheta%20%7D%7D%20%5Capprox%20%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bn%3D1%7D%5E%7BN%7DR_%7B%5Ctau%5E%7Bn%7D%7D%20%5Cnabla%20log%20P_%7B%28%5Ctau%5E%7Bn%7D%5Cmid%5Ctheta%29%20%7D)                              **1.6**

现在我们有了策略梯度的一个基本式子，但是这个式子还不够清楚，因为每一条轨迹的概率是可以更细化的去算的。现在我们将 $P_{(\tau^{n}\mid\theta) }$ 展开(公式太长，这里直接截用李宏毅老师上课的PPT中的公式)

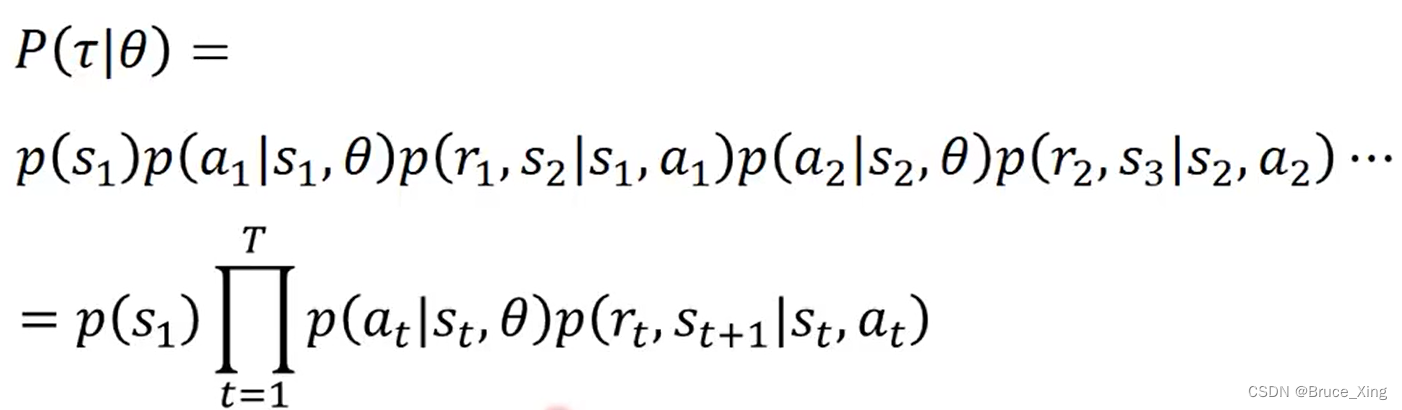
遇到长的式子不要慌，先看最长的那一行

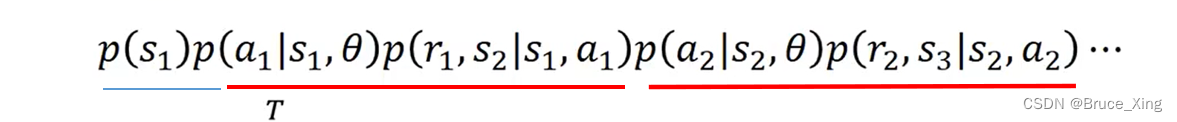
其实这是一个很直觉的公式，我们一项一项看：

$p(s_{_{1}})$ 初始状态s1的概率
$p(a_{_{1}} \mid s_{1},\theta)$ 基于这个状态s1和参数** $\theta$ **选择动作a1的概率
$p(r_{_{1}},s_{2} \mid s_{1},a_{1})$ 基于动作a1和s1，得到奖励函数r1,然后状态转移到s2

后面就是循环往复。在看这个式子

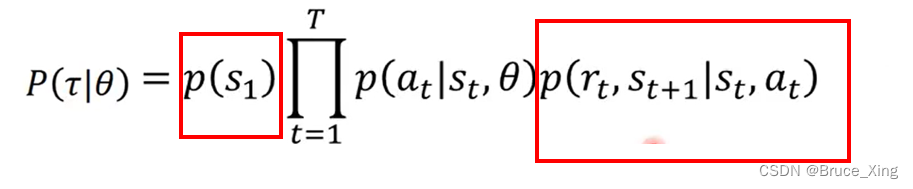
我们现在要先两边取log，这样可以把相乘换成相加，式子就变成了如下

其中红色框这一项和 $\theta$ 没有关系，然后两边对** $\theta$ **求梯度就可以消去和 $\theta$ 无关的项。整个式子就变成了如下

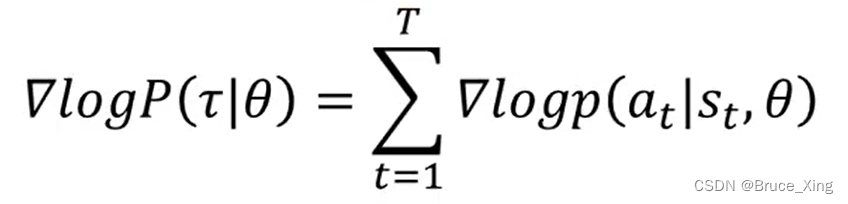
把上面的式子带入式子1.6，就得到了一个完整的可用的梯度公式

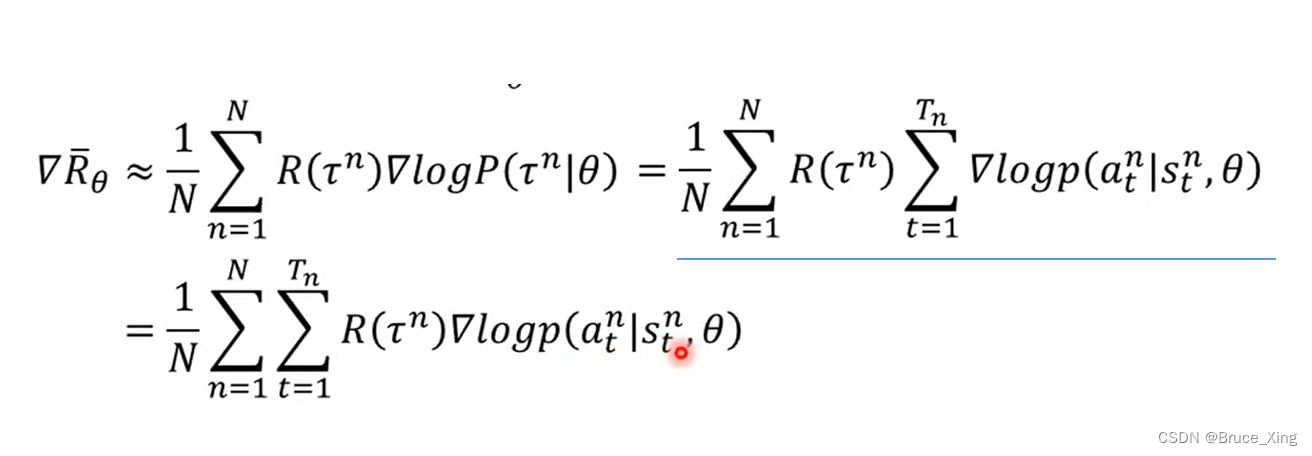
其中我们还是稍稍做了一点改变，

这个式子也很好理解，一条轨迹的概率不就是这条轨迹每一个采取某个动作基于某一个状态概率的相乘，但是因为取了log这里就变成了相加，用了求和符号。现在再回过头看看那一大串的公式，这里附加一张图以便理解，现在这当中的每一步相信就非常清楚了。

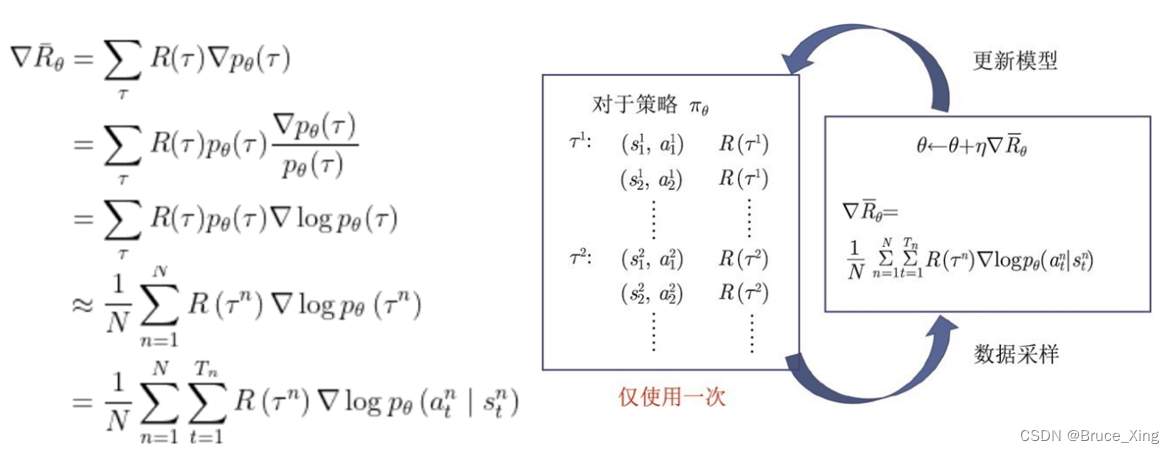
然后去做梯度上升就更新** $\theta$ **啦，整个式子的推导就完成了。

$\theta^{new} \leftarrow \theta^{old}+ \eta \nabla{\bar{R}}_{ \theta{old}}$

直观的理解

我们再来看这个最重要的式子

这个式子看起来很复杂，直观上可以理解为如果在 $\tau^{^{n}}$ 这个轨迹中，agent在玩到第t步时，看到了 $s{_{t}^{n}}$ ，采取了一个动作 $a{_{t}^{n}}$ ，

最后的 $R_{(\tau^{n})}$ 是正的，就更新 $\theta$ 去提升 $p(a_{t}^{n}\mid s_{t}^{n})$ 概率

最后的 $R_{(\tau^{n})}$ 是负的，就更新 $\theta$ 去降低 $p(a_{t}^{n}\mid s_{t}^{n})$ 概率

终于policy gradient的基本思路就讲清楚了！！

随之而来的问题

但是，又是但是😭😭，这里还会有几个小问题。

Q1：为什么要用log呀，就是单纯的简化计算吗?

Q2: 万一 $\bar{R}{_{\theta }}$ 都是正的会影响结果吗？

Q3：用整个 episode，或者说一条轨迹的reward评价一个其中的一个pair $a_{t} \mid s_{t}$ 的好坏合理吗？换句话说，我整局游戏输了，难道我的每一步操作都是错的吗？

为了下一步的学习PPO，这几个问题还必须要解决，但是李宏毅老师已经把这几个问题讲的非常清楚了，这里我截取其中的图片再稍微解释一下。如果想去看视频的也可以：这里恰个链接，不想去也可以往下看
Deep Reinforcemen Learning(3_1)_哔哩哔哩_bilibiliDeep Reinforcemen Learning(3_1)是李宏毅2020机器学习深度学习(完整版)国语的第108集视频，该合集共计119集，视频收藏或关注UP主，及时了解更多相关视频内容。https://www.bilibili.com/video/BV1JE411g7XF?p=108&vd_source=30e162a938f0ff832e2713d1b1f6640f**Q1：**为什么要用log呀，就是单纯的简化计算吗?

首先我们先理解log，再求梯度中根据链式法则用log其实等于做了一个normalization

                             ![log p(a_{t}^{n} \mid s_{t}^{n},\theta ) = \frac{ \nabla p(a_{t}^{n} \mid s_{t}^{n},\theta ) }{p(a_{t}^{n} \mid s_{t}^{n},\theta ) }](https://latex.csdn.net/eq?log%20p%28a_%7Bt%7D%5E%7Bn%7D%20%5Cmid%20s_%7Bt%7D%5E%7Bn%7D%2C%5Ctheta%20%29%20%3D%20%5Cfrac%7B%20%5Cnabla%20p%28a_%7Bt%7D%5E%7Bn%7D%20%5Cmid%20s_%7Bt%7D%5E%7Bn%7D%2C%5Ctheta%20%29%20%7D%7Bp%28a_%7Bt%7D%5E%7Bn%7D%20%5Cmid%20s_%7Bt%7D%5E%7Bn%7D%2C%5Ctheta%20%29%20%7D)                                    **1.7**

怎么理解呢，上图！

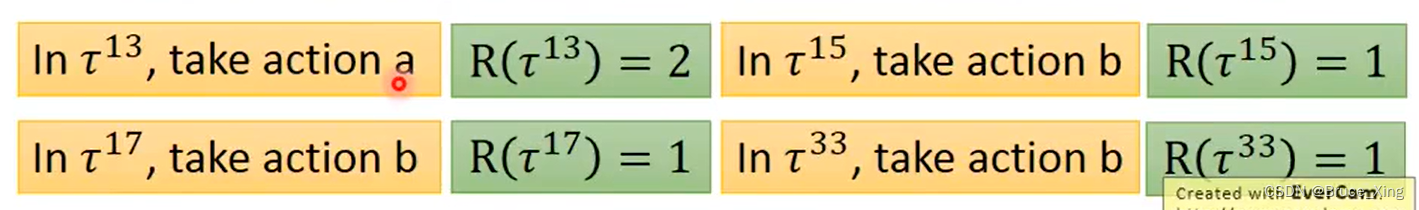
在四次轨迹中，a被sample了一次，b被sample了三次。a对应的轨迹奖励是2，b是1。

其实我们应该提升a的概率，因为奖励高嘛！但是因为b被sample3次，也就被提升了三次，a的奖励虽然大但是只被提升了一次。随后选择动作b的概率相对a的概率竟然提升了😰😰，这肯定会影响结果。根据式1.7，就可以解决这个问题，不光计算梯度，还要除以对应的概率。这个问题就可以被解决。

** Q2: **万一 $\bar{R}{_{\theta }}$ 都是正的会影响结果吗？

其实理想状态是不会的影响的，如果每一个action都被sample到，那就都提升，其实也就没有问题。但是如果有一个没有sample到就坏了，概率关系就不对了。

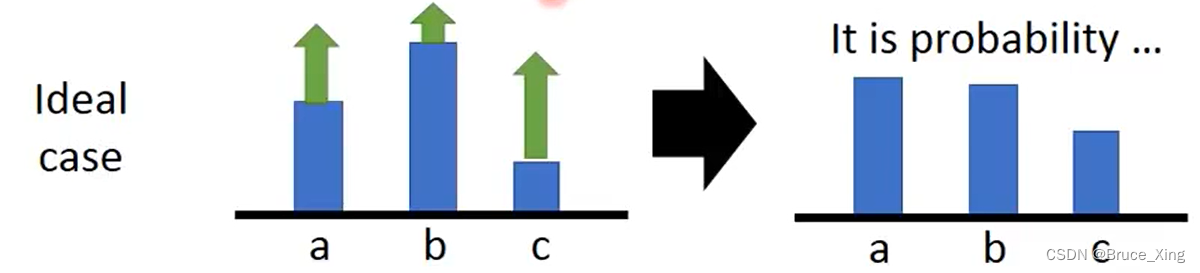
这个时候我们只要添加一个baseline就可以了

这样就可以有正有负，不光只有提升还有下降，相对关系是正确的就可以。至于这个b的选择可以约等于 ≈ sample到每条轨迹的奖励的均值，这里先不做过多解释，后面实际用到时在详解。红色框这一项非常重要，又称为优势函数，下一节我们会用到

Q3：用整个 episode的reward表示一个pair $a_{t} \mid s_{t}$ 的好坏合理吗？换句话说，我整局游戏输了，难道我的每一步操作都是错的吗？

这个问题从直觉上我们觉得是不对的，实际也是不准的。我整局游戏虽然输了，但是可能也有很精彩的操作啊，就像玩OW，麦克雷枪枪爆头😁😁，就是最后放大空了，游戏输了，很明显枪枪爆头是好的操作，应当提升这个概率。如何解决呢，我们可以计算从某一个action往后的奖励，看看这个action对之后有什么影响，再加上一个折扣，来当做正确的奖励值。替换如下：

如果这个奖励的计算你还是觉得有点懵，可以再看看下面这张图，是否会更多的理解：

更新中。。。喜欢请多支持

标签：深度学习人工智能

本文转载自: https://blog.csdn.net/BruceXee/article/details/128435769
版权归原作者 Bruce_Xing 所有，如有侵权，请联系我们删除。