【安全密钥交换协议】基尔霍夫定律-约翰逊噪声（KLJN）方案的随机数生成器攻击研究（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

*🏆博主优势：🌞🌞🌞*博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

文献来源：

本文旨在深入研究基尔霍夫定律-约翰逊噪声（KLJN）安全密钥交换方案，并针对该方案提出两种新的攻击方法。这些攻击方法都基于对随机数生成器的安全性进行破坏。

首先，我们讨论了一种情况，即夏娃知道艾丽丝和鲍勃的随机数生成器的种子。在这种情况下，我们展示了即使夏娃的电流和电压测量只有一位分辨率，她也可以在比特交换周期的一小部分内破解安全密钥比特。这表明即使在有限的信息条件下，攻击者仍然可以对该方案进行破坏。

其次，我们探讨了另一种情况，即夏娃只知道艾丽丝的随机数生成器的种子。在这种情况下，我们展示了夏娃仍然可以破解安全密钥比特，但她需要使用整个比特交换周期来进行攻击。这表明即使在更有限的信息条件下，攻击者仍然有可能对该方案进行攻击。

通过这些攻击方法的研究，我们可以更好地了解KLJN安全密钥交换方案的脆弱性，并为进一步加强该方案的安全性提供重要的参考。我们希望这些研究成果能够引起学术界和工业界对该方案安全性的关注，并推动相关领域的进一步发展和创新。

结论：

安全密钥交换协议利用随机数，而受损的随机数会导致信息泄露。迄今为止，人们不知道Eve如何利用受损的随机数生成器来攻击KLJN协议。为了展示Eve如何利用受损的随机数生成器，我们介绍了对KLJN方案的两种简单攻击。我们表明，如果Eve知道艾丽丝和鲍勃的随机数生成器的种子，也就是说，她确切地知道这些随机数，即使她的测量只有一位分辨率，她也可以破解比特交换。这种情况类似于基于噪声的逻辑系统中的字符串验证。破解交换的比特的速度呈指数级增长；Eve可以在比特交换周期的一小部分内提取比特，因此Eve将比只知道自己随机数的艾丽丝和鲍勃更快地了解交换的比特。我们还表明，即使Eve只知道艾丽丝的随机数生成器的种子，她仍然可以破解安全比特，但她需要利用整个比特交换周期。需要注意的是：
• 这个演示是在假设理想的KLJN方案的情况下进行的。未来的工作将涉及使用电缆模拟器以及相关的延迟和瞬变进行实际实现。
• Eve对随机数的确定性知识是一种强大的安全漏洞，但这是展示此类攻击如何发展的一种说明性方式；
• 开放问题是Eve对随机数的知识只是统计性的新攻击方案。

📚****2 运行结果

2.1 算例1

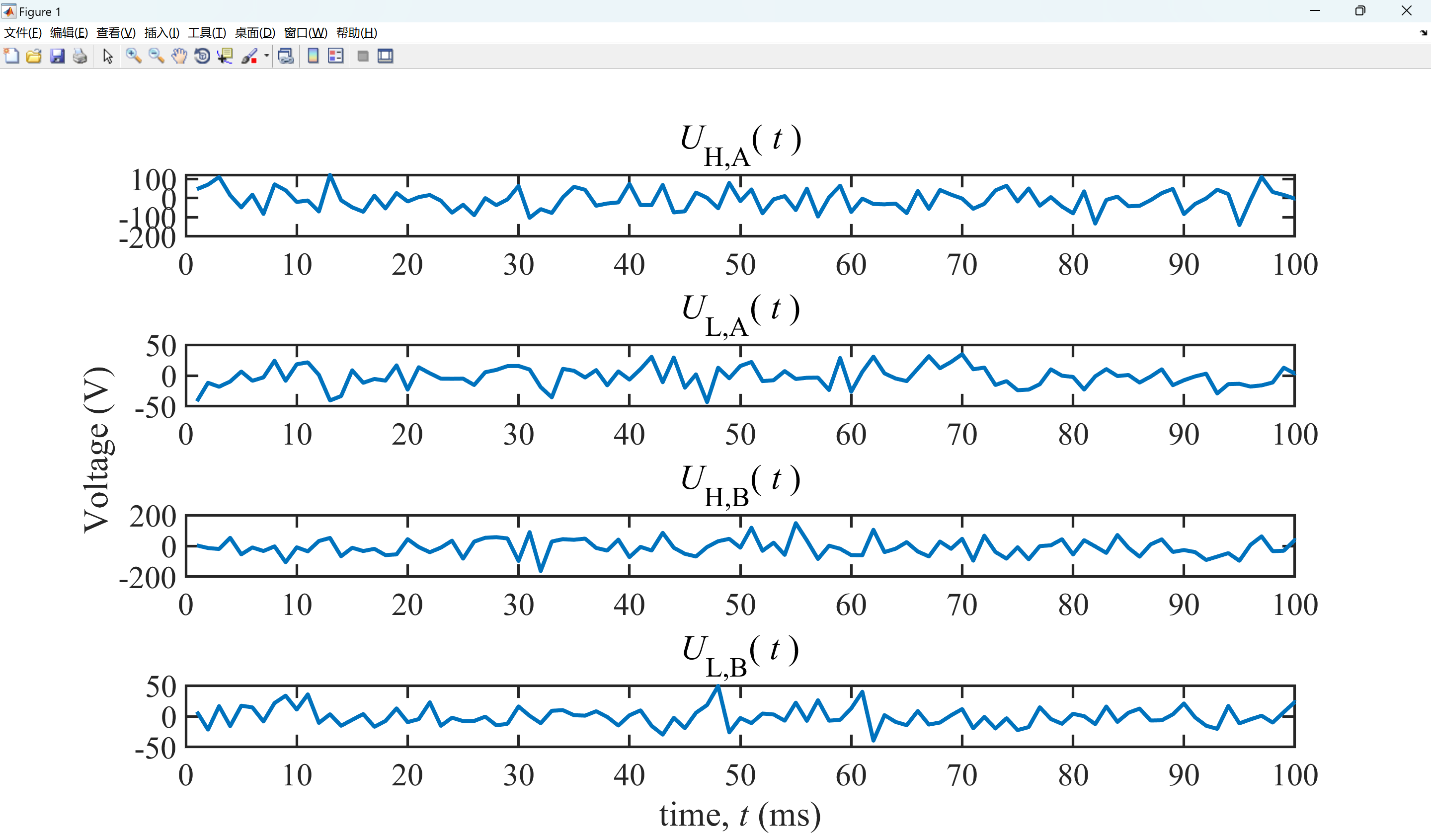
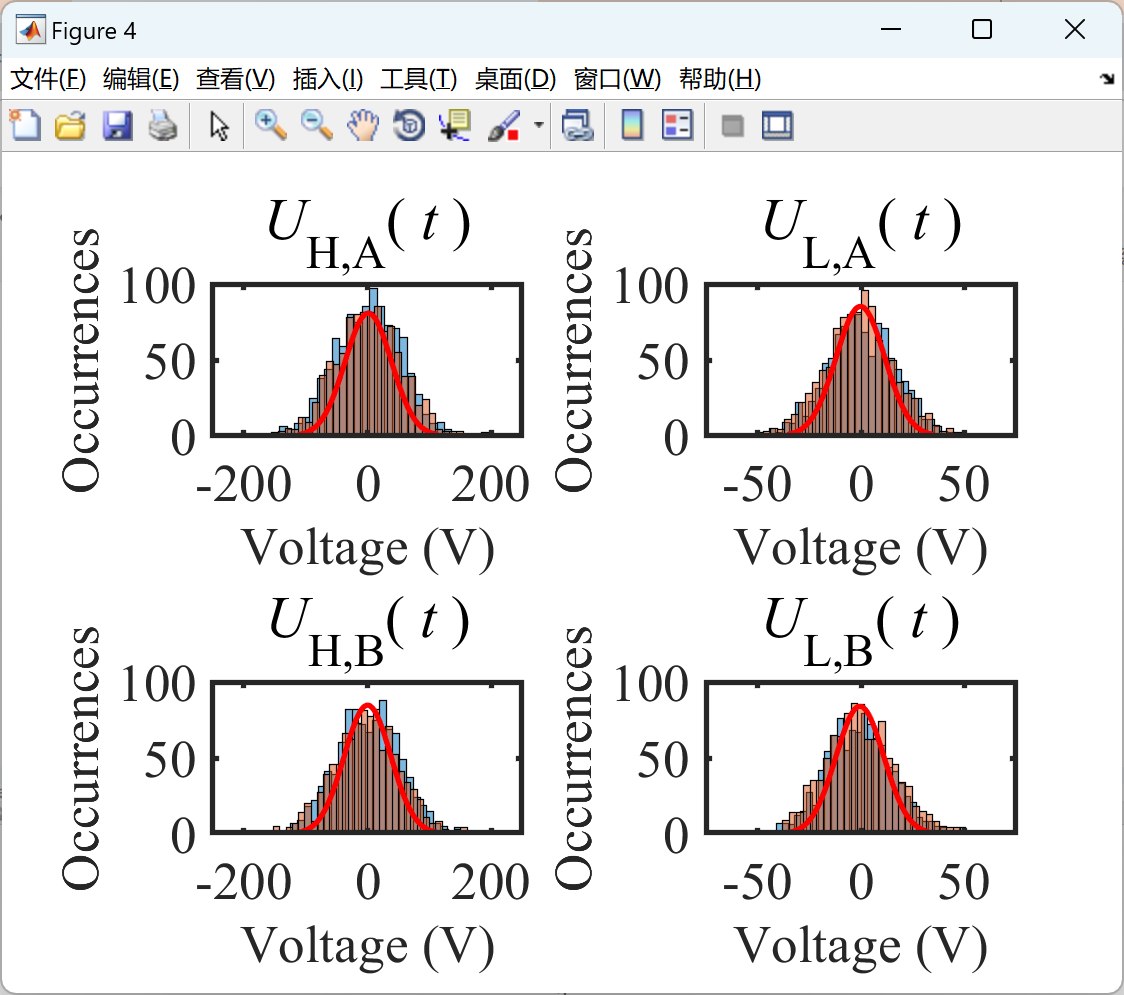
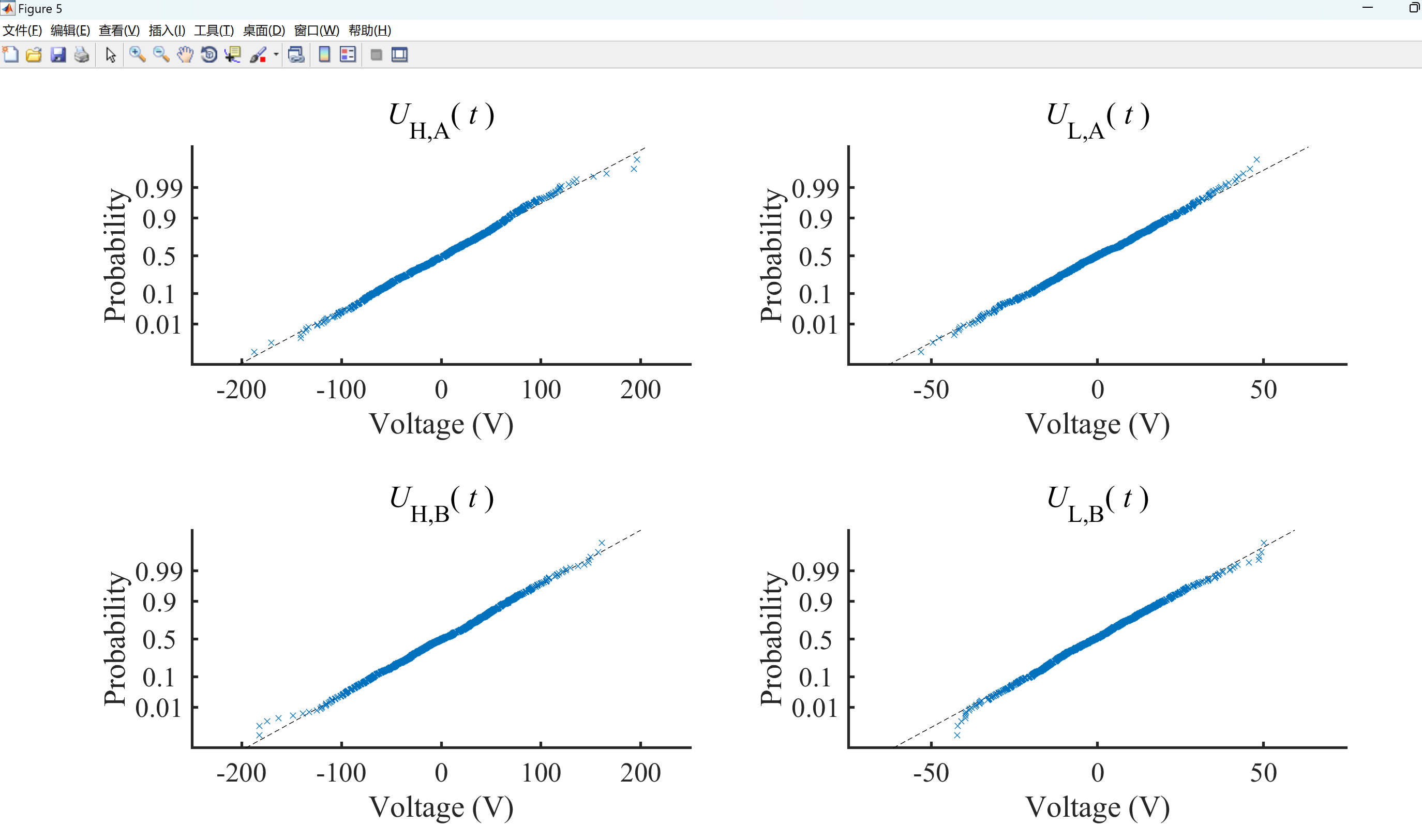
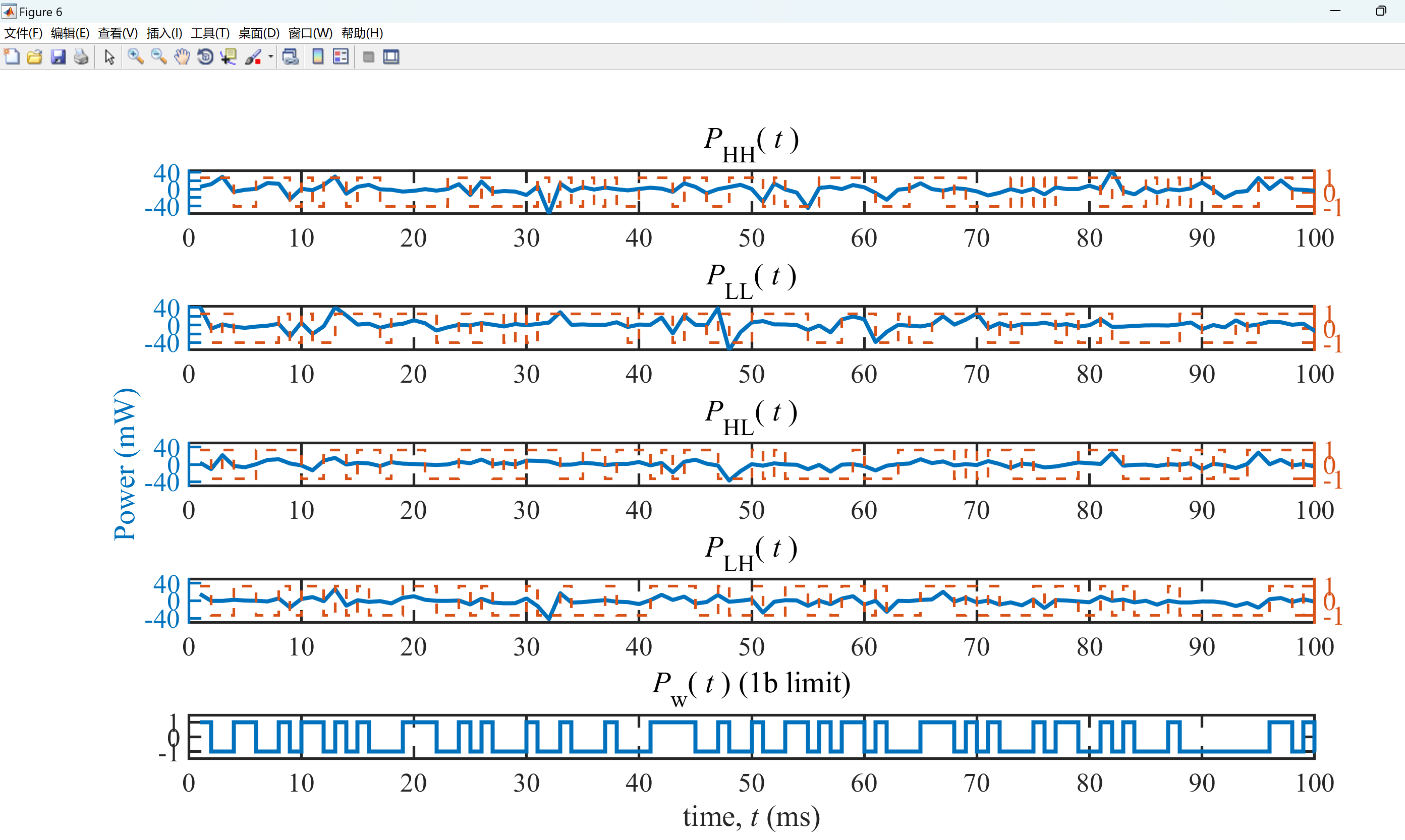
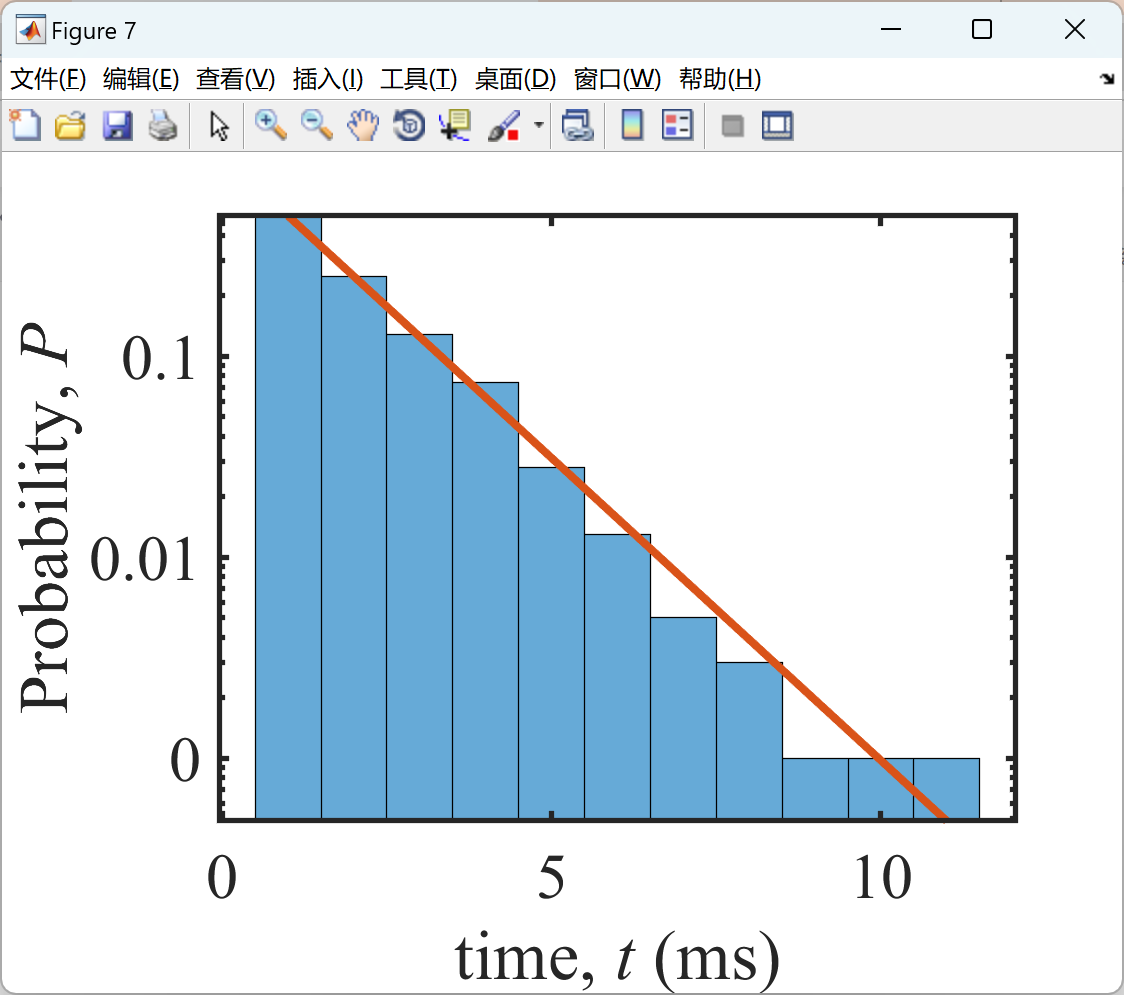
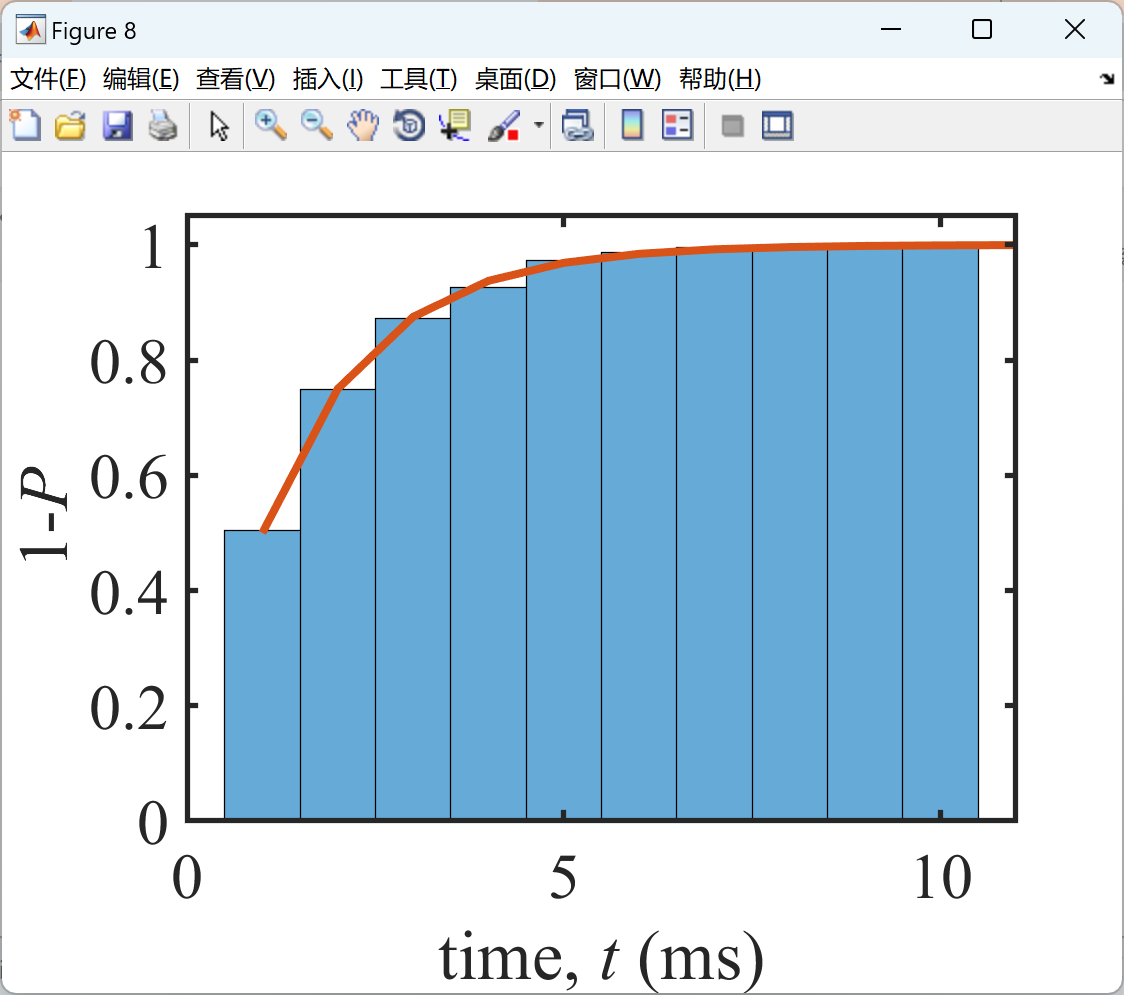
2.2 算例2

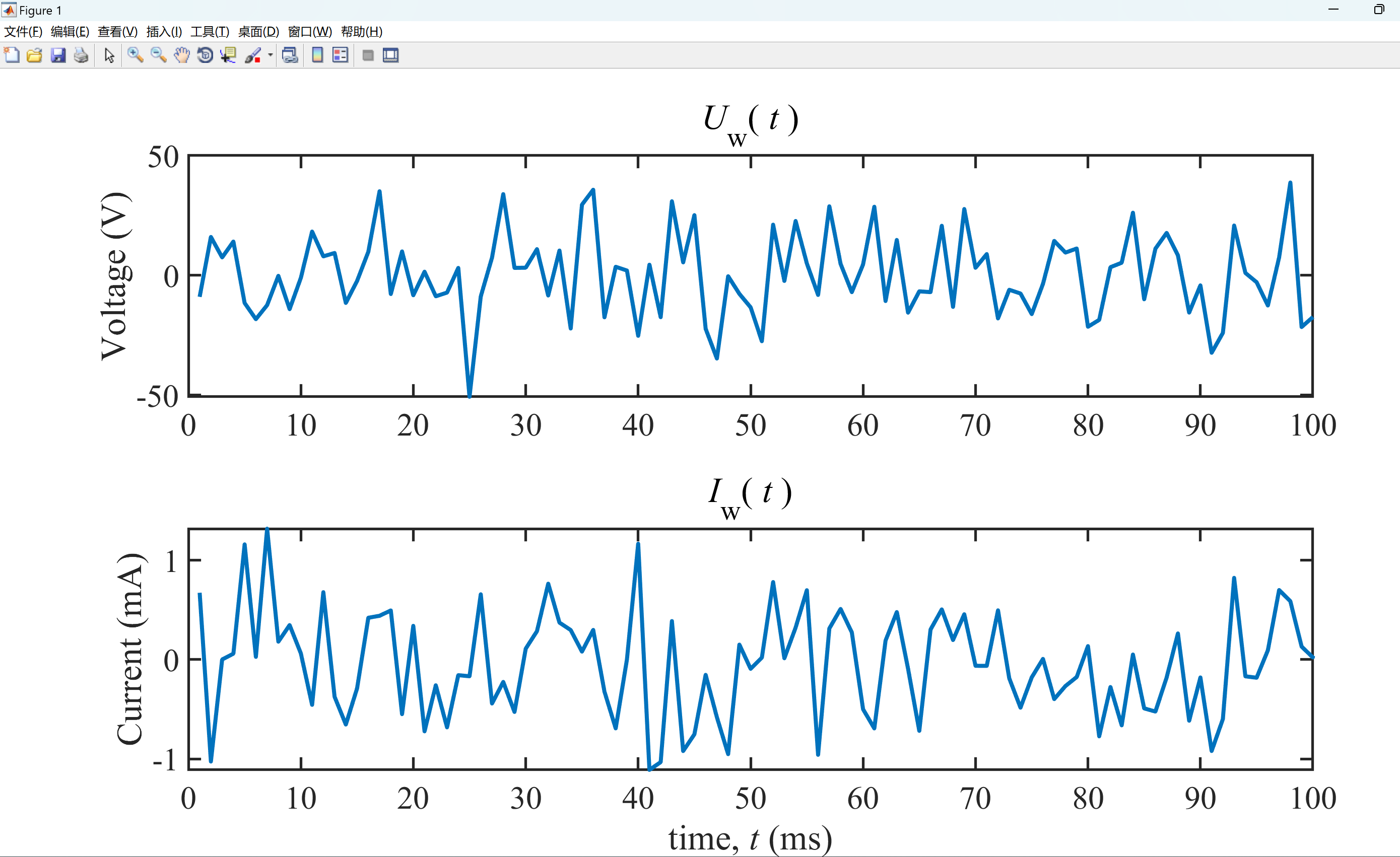
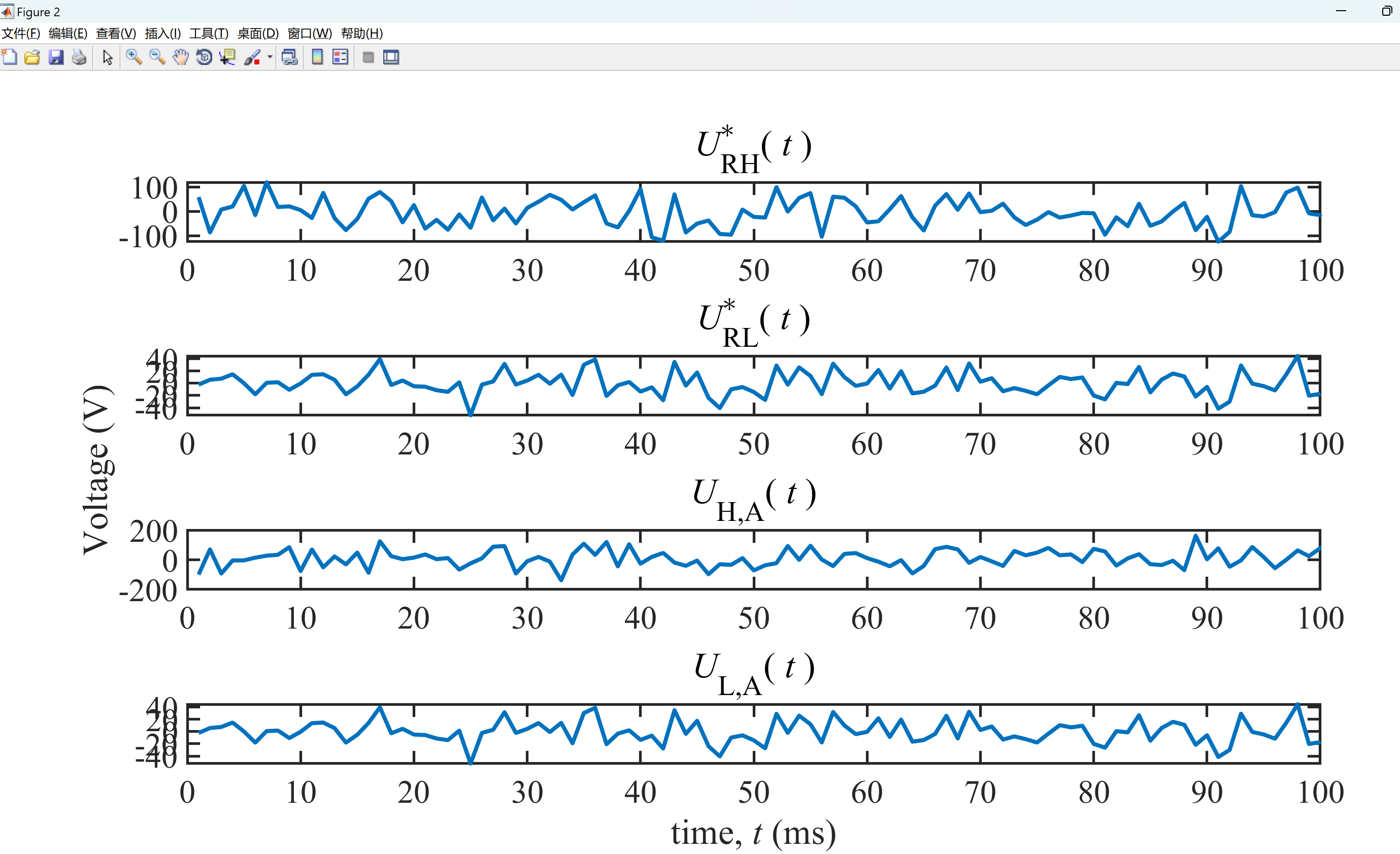
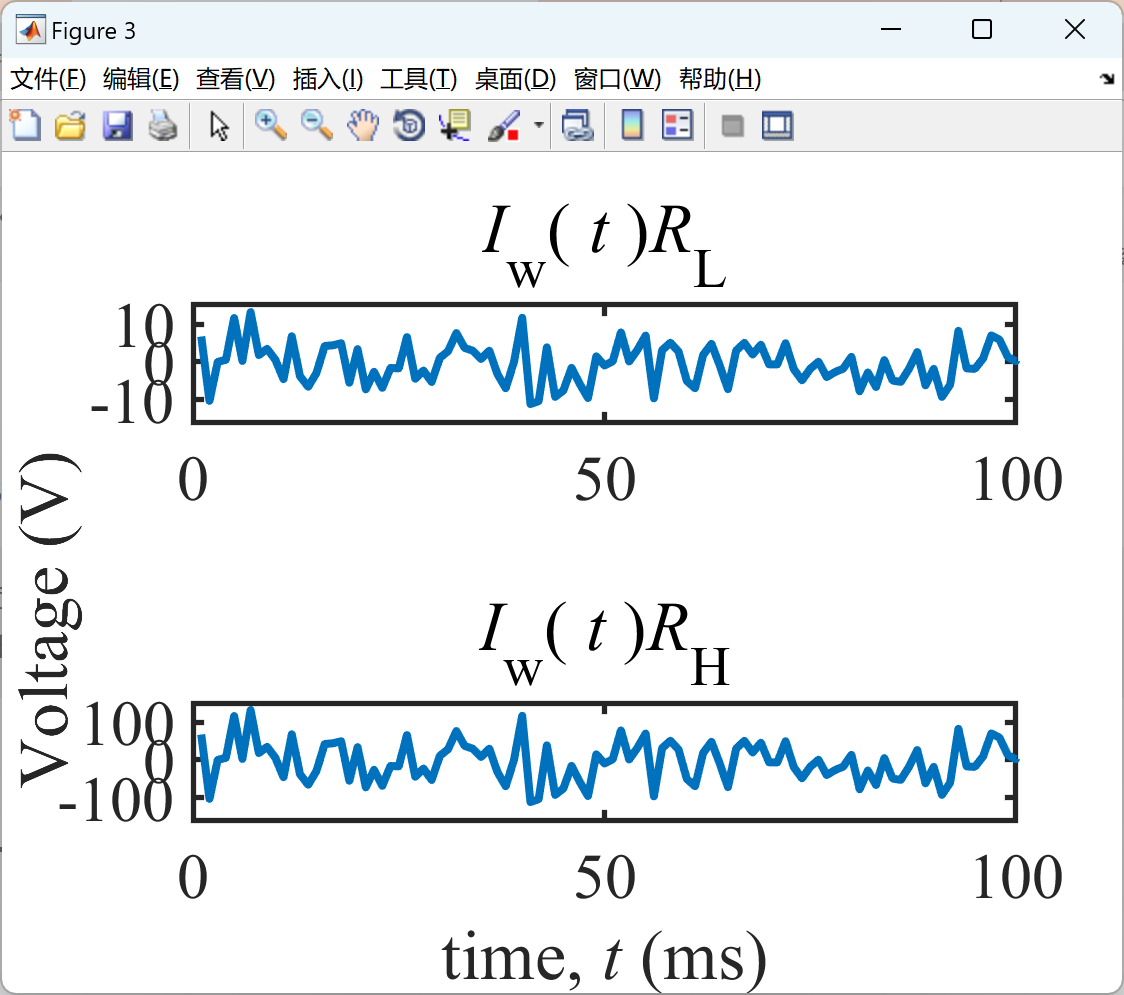
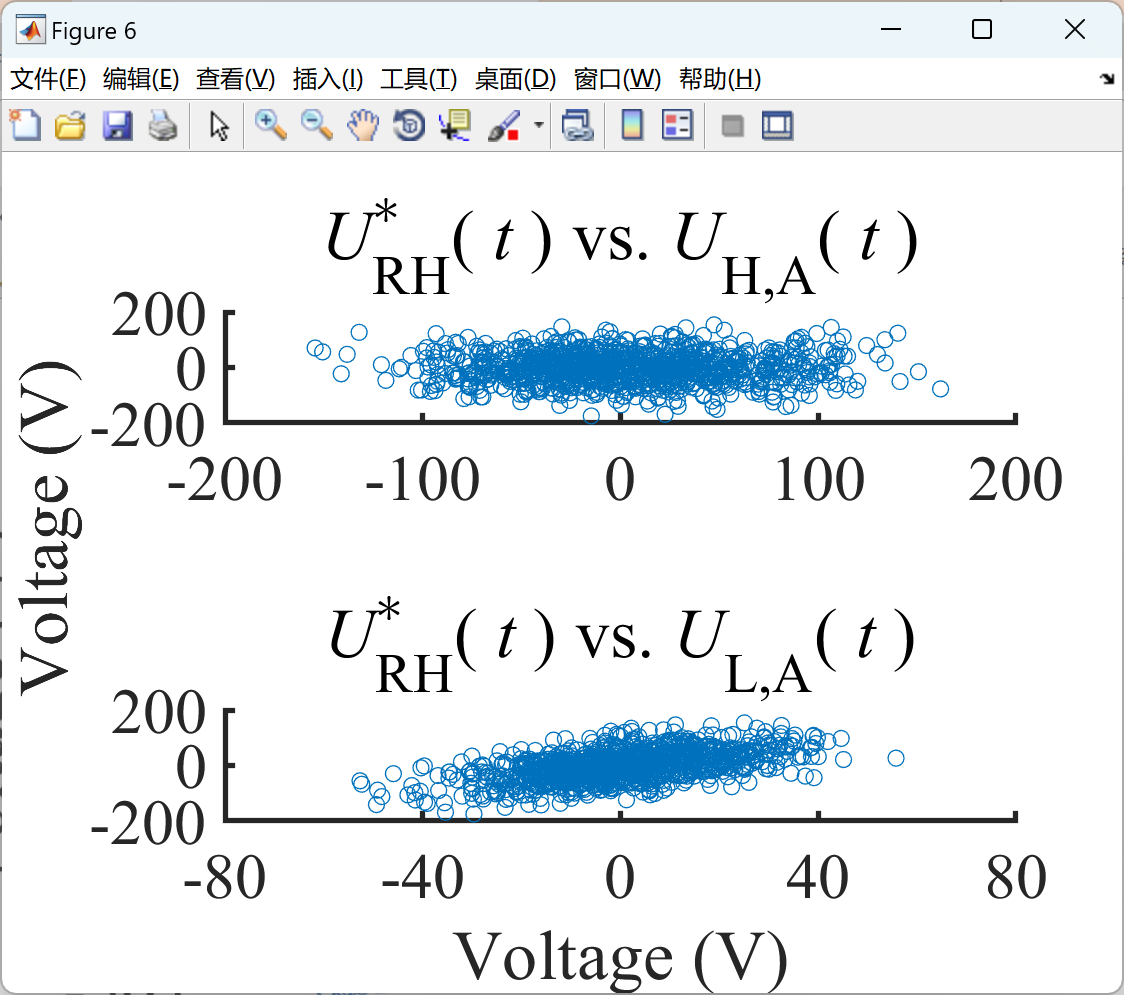
2.3 算例3

部分代码：

%let's plot the voltages
figure;
set(gca, 'FontName', 'Times New Roman')
set(gcf,'color','w');
subplot(4,1,1);
plot(UAH,'Linewidth',3);
%xlabel('(a)','Fontsize',14);
xlim([0 100]);
%ylabel('Volts (V)');
title('\it{U}{\rm{H,A}}\rm{(}\it{ t }\rm{)}','Fontsize',28);
set(gca, 'FontName', 'Times New Roman')
set(gca,'fontsize', 24);
set(gca,'linewidth',2)
subplot(4,1,2);
plot(UAL,'Linewidth',3);
%xlabel('(b)','Fontsize',14);
xlim([0 100]);
%ylim([-7.5 7.5]);
%ylabel('Volts (V)');
title('\it{U}{\rm{L,A}}\rm{(}\it{ t }\rm{)}','Fontsize',28);
set(gca, 'FontName', 'Times New Roman')
set(gca,'fontsize', 24);
set(gca,'linewidth',2)
subplot(4,1,3);
plot(UBH,'Linewidth',3);
%xlabel('(c)','Fontsize',14);
xlim([0 100]);
ylabel(' Voltage (V)');
title('\it{U}{\rm{H,B}}\rm{(}\it{ t }\rm{)}','Fontsize',28);
set(gca, 'FontName', 'Times New Roman')
set(gca,'fontsize', 24);
set(gca,'linewidth',2)
subplot(4,1,4);
plot(UBL,'Linewidth',3);
xlabel('time, \it{t}\rm{ (ms)}','Fontsize',24);
set(gca, 'FontName', 'Times New Roman')
xlim([0 100]);
%ylim([-7.5 7.5]);
%ylabel('Volts (V)');
title('\it{U}{\rm{L,B}}\rm{(}\it{ t }\rm{)}','Fontsize',18);
set(gca, 'FontName', 'Times New Roman')
set(gca,'fontsize', 24);
set(gca,'linewidth',2)

%why not power spectral density and mean-square voltage?
%PSD
%YAH = fft(linspace(rms(UAH),rms(UAH),n).^2/fB);
%P2AH = abs(YAH/n);
%P1AH = P2AH(1:n/2+1);
%P1AH(2:end-1) = 2P1AH(2:end-1);
P1AH = linspace(rms(UAH),rms(UAH),n);
P1AH = P1AH.^2/fB;
%YAL = fft(linspace(rms(UAL),rms(UAL),n).^2/fB);
%P2AL = abs(YAL/n);
%P1AL = P2AL(1:n/2+1);
%P1AL(2:end-1) = 2P1AL(2:end-1);
P1AL = linspace(rms(UAL),rms(UAL),n);
P1AL = P1AL.^2/fB;
%YBH = fft(linspace(rms(UBH),rms(UBH),n).^2/fB);
%P2BH = abs(YBH/n);
%P1BH = P2BH(1:n/2+1);
%P1BH(2:end-1) = 2P1BH(2:end-1);
P1BH = linspace(rms(UBH),rms(UBH),n);
P1BH = P1BH.^2/fB;
%YBL = fft(linspace(rms(UBL),rms(UBL),n).^2/fB);
%P2BL = abs(YBL/n);
%P1BL = P2BL(1:n/2+1);
%P1BL(2:end-1) = 2P1BL(2:end-1);
P1BL = linspace(rms(UBL),rms(UBL),n);
P1BL = P1BL.^2/fB;
figure;
set(gca, 'FontName', 'Times New Roman')
set(gcf,'color','w');
subplot(4,1,1);
plot(P1AH/1e-3,'Linewidth',3)
title('\it{S}{\rm{H,A}}\rm{(}\it{ f }\rm{)}','Fontsize',18);
set(gca, 'FontName', 'Times New Roman')
set(gca,'fontsize', 14);
set(gca,'linewidth',2)
%xlabel('f (Hz)','Fontsize',14)
xlim([10 100]);
ylabel('Power/10^{-3} (V^{2}/Hz)','Fontsize',14)
subplot(4,1,2);
plot(P1AL/1e-3,'Linewidth',3)
title('\it{S}{\rm{L,A}}\rm{(}\it{ f }\rm{)}','Fontsize',18);
set(gca, 'FontName', 'Times New Roman')
set(gca,'fontsize', 14);
set(gca,'linewidth',2)
%xlabel('f (Hz)','Fontsize',14)

🎉3**** 参考文献****

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、数据、文献