深度学习中的优化算法之AdaMax

  之前在https://blog.csdn.net/fengbingchun/article/details/125018001 介绍过深度学习中的优化算法Adam，这里介绍下深度学习的另一种优化算法AdaMax。AdaMax与Adam来自于同一篇论文。论文名字为《ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION》，论文地址：https://arxiv.org/pdf/1412.6980.pdf

  **AdaMax：是梯度优化算法的扩展，基于无穷范数的Adam****的变体(a variant of Adam based on the infinity norm)**。此算法对学习率的上限提供了一个更简单的范围，并可能对某些问题进行更有效的优化。如下图所示，截图来自：https://arxiv.org/pdf/1609.04747.pdf

  **AdaMax与Adam区别：本质上前者是将L2范数推广到L-infinity****范数**。AdaMax与Adam最终公式中仅分母的计算方式不同，AdaMax使用公式24，Adam使用公式20。

以下是与Adam不同的代码片段：

  1.在原有枚举类Optimizaiton的基础上新增AdaMax：

enum class Optimization {
    BGD, // Batch Gradient Descent
    SGD, // Stochastic Gradient Descent
    MBGD, // Mini-batch Gradient Descent
    SGD_Momentum, // SGD with Momentum
    AdaGrad, // Adaptive Gradient
    RMSProp, // Root Mean Square Propagation
    Adadelta, // an adaptive learning rate method
    Adam, // Adaptive Moment Estimation
    AdaMax // a variant of Adam based on the infinity norm
};

  2.calculate_gradient_descent函数：

void LogisticRegression2::calculate_gradient_descent(int start, int end)
{
    switch (optim_) {
        case Optimization::AdaMax: {
            int len = end - start;
            std::vector<float> m(feature_length_, 0.), u(feature_length_, 1e-8), mhat(feature_length_, 0.);
            std::vector<float> z(len, 0.), dz(len, 0.);
            float beta1t = 1.;
            for (int i = start, x = 0; i < end; ++i, ++x) {
                z[x] = calculate_z(data_->samples[random_shuffle_[i]]);
                dz[x] = calculate_loss_function_derivative(calculate_activation_function(z[x]), data_->labels[random_shuffle_[i]]);

                beta1t *= beta1_;

                for (int j = 0; j < feature_length_; ++j) {
                    float dw = data_->samples[random_shuffle_[i]][j] * dz[x];
                    m[j] = beta1_ * m[j] + (1. - beta1_) * dw; // formula 19
                    u[j] = std::max(beta2_ * u[j], std::fabs(dw)); // formula 24

                    mhat[j] = m[j] / (1. - beta1t); // formula 20

                    // Note: need to ensure than u[j] cannot be 0.
                    // (1). u[j] is initialized to 1e-8, or
                    // (2). if u[j] is initialized to 0., then u[j] adjusts to (u[j] + 1e-8)
                    w_[j] = w_[j] - alpha_ * mhat[j] / u[j]; // formula 25
                }

                b_ -= (alpha_ * dz[x]);
            }
        }
            break;
        case Optimization::Adam: {
            int len = end - start;
            std::vector<float> m(feature_length_, 0.), v(feature_length_, 0.), mhat(feature_length_, 0.), vhat(feature_length_, 0.);
            std::vector<float> z(len, 0.), dz(len, 0.);
            float beta1t = 1., beta2t = 1.;
            for (int i = start, x = 0; i < end; ++i, ++x) {
                z[x] = calculate_z(data_->samples[random_shuffle_[i]]);
                dz[x] = calculate_loss_function_derivative(calculate_activation_function(z[x]), data_->labels[random_shuffle_[i]]);

                beta1t *= beta1_;
                beta2t *= beta2_;

                for (int j = 0; j < feature_length_; ++j) {
                    float dw = data_->samples[random_shuffle_[i]][j] * dz[x];
                    m[j] = beta1_ * m[j] + (1. - beta1_) * dw; // formula 19
                    v[j] = beta2_ * v[j] + (1. - beta2_) * (dw * dw); // formula 19

                    mhat[j] = m[j] / (1. - beta1t); // formula 20
                    vhat[j] = v[j] / (1. - beta2t); // formula 20

                    w_[j] = w_[j] - alpha_ * mhat[j] / (std::sqrt(vhat[j]) + eps_); // formula 21
                }

                b_ -= (alpha_ * dz[x]);
            }
        }
            break;
        case Optimization::Adadelta: {
            int len = end - start;
            std::vector<float> g(feature_length_, 0.), p(feature_length_, 0.);
            std::vector<float> z(len, 0.), dz(len, 0.);
            for (int i = start, x = 0; i < end; ++i, ++x) {
                z[x] = calculate_z(data_->samples[random_shuffle_[i]]);
                dz[x] = calculate_loss_function_derivative(calculate_activation_function(z[x]), data_->labels[random_shuffle_[i]]);

                for (int j = 0; j < feature_length_; ++j) {
                    float dw = data_->samples[random_shuffle_[i]][j] * dz[x];
                    g[j] = mu_ * g[j] + (1. - mu_) * (dw * dw); // formula 10

                    float alpha = (eps_ + std::sqrt(p[j])) / (eps_ + std::sqrt(g[j]));
                    float change = alpha * dw;
                    p[j] = mu_ * p[j] +  (1. - mu_) * (change * change); // formula 15

                    w_[j] = w_[j] - change;
                }

                b_ -= (eps_ * dz[x]);
            }
        }
            break;
        case Optimization::RMSProp: {
            int len = end - start;
            std::vector<float> g(feature_length_, 0.);
            std::vector<float> z(len, 0), dz(len, 0);
            for (int i = start, x = 0; i < end; ++i, ++x) {
                z[x] = calculate_z(data_->samples[random_shuffle_[i]]);
                dz[x] = calculate_loss_function_derivative(calculate_activation_function(z[x]), data_->labels[random_shuffle_[i]]);

                for (int j = 0; j < feature_length_; ++j) {
                    float dw = data_->samples[random_shuffle_[i]][j] * dz[x];
                    g[j] = mu_ * g[j] + (1. - mu_) * (dw * dw); // formula 18
                    w_[j] = w_[j] - alpha_ * dw / (std::sqrt(g[j]) + eps_);
                }

                b_ -= (alpha_ * dz[x]);
            }
        }
            break;
        case Optimization::AdaGrad: {
            int len = end - start;
            std::vector<float> g(feature_length_, 0.);
            std::vector<float> z(len, 0), dz(len, 0);
            for (int i = start, x = 0; i < end; ++i, ++x) {
                z[x] = calculate_z(data_->samples[random_shuffle_[i]]);
                dz[x] = calculate_loss_function_derivative(calculate_activation_function(z[x]), data_->labels[random_shuffle_[i]]);

                for (int j = 0; j < feature_length_; ++j) {
                    float dw = data_->samples[random_shuffle_[i]][j] * dz[x];
                    g[j] += dw * dw;
                    w_[j] = w_[j] - alpha_ * dw / (std::sqrt(g[j]) + eps_);
                }

                b_ -= (alpha_ * dz[x]);
            }
        }
            break;
        case Optimization::SGD_Momentum: {
            int len = end - start;
            std::vector<float> change(feature_length_, 0.);
            std::vector<float> z(len, 0), dz(len, 0);
            for (int i = start, x = 0; i < end; ++i, ++x) {
                z[x] = calculate_z(data_->samples[random_shuffle_[i]]);
                dz[x] = calculate_loss_function_derivative(calculate_activation_function(z[x]), data_->labels[random_shuffle_[i]]);

                for (int j = 0; j < feature_length_; ++j) {
                    float new_change = mu_ * change[j] - alpha_ * (data_->samples[random_shuffle_[i]][j] * dz[x]);
                    w_[j] += new_change;
                    change[j] = new_change;
                }

                b_ -= (alpha_ * dz[x]);
            }
        }
            break;
        case Optimization::SGD:
        case Optimization::MBGD: {
            int len = end - start;
            std::vector<float> z(len, 0), dz(len, 0);
            for (int i = start, x = 0; i < end; ++i, ++x) {
                z[x] = calculate_z(data_->samples[random_shuffle_[i]]);
                dz[x] = calculate_loss_function_derivative(calculate_activation_function(z[x]), data_->labels[random_shuffle_[i]]);

                for (int j = 0; j < feature_length_; ++j) {
                    w_[j] = w_[j] - alpha_ * (data_->samples[random_shuffle_[i]][j] * dz[x]);
                }

                b_ -= (alpha_ * dz[x]);
            }
        }
            break;
        case Optimization::BGD:
        default: // BGD
            std::vector<float> z(m_, 0), dz(m_, 0);
            float db = 0.;
            std::vector<float> dw(feature_length_, 0.);
            for (int i = 0; i < m_; ++i) {
                z[i] = calculate_z(data_->samples[i]);
                o_[i] = calculate_activation_function(z[i]);
                dz[i] = calculate_loss_function_derivative(o_[i], data_->labels[i]);

                for (int j = 0; j < feature_length_; ++j) {
                    dw[j] += data_->samples[i][j] * dz[i]; // dw(i)+=x(i)(j)*dz(i)
                }
                db += dz[i]; // db+=dz(i)
            }

            for (int j = 0; j < feature_length_; ++j) {
                dw[j] /= m_;
                w_[j] -= alpha_ * dw[j];
            }

            b_ -= alpha_*(db/m_);
    }
}

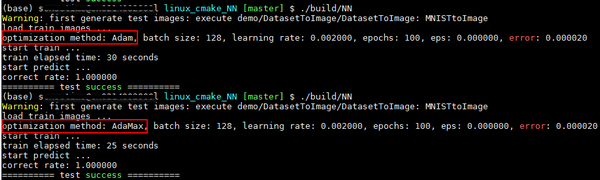
  执行结果如下图所示：测试函数为test_logistic_regression2_gradient_descent，多次执行每种配置，最终结果都相同。图像集使用MNIST，其中训练图像总共10000张，0和1各5000张，均来自于训练集；预测图像总共1800张，0和1各900张，均来自于测试集。Adam和AdaMax配置参数相同的情况下，即eps为1e-8，学习率为0.002，beta1为0.9，beta2为0.999的情况下，Adam耗时30秒，AdaMax耗时为25秒；它们的识别率均为100%

 ** GitHub**： https://github.com/fengbingchun/NN_Test