Torch中常见插值方式及各自的优缺点

Pytorch常见插值方式及优缺点

1 插值算法

插值指的是利用已知数据去预测未知数据，图像插值则是给定一个像素点，根据它周围像素点的信息来对该像素点的值进行预测。
当我们调整图片尺寸或者对图片变形的时候常会用到图片插值。

常见的插值算法可以分为两类：自适应和非自适应。 自适应的方法可以根据插值的内容来改变（尖锐的边缘或者是平滑的纹理），非自适应的方法对所有的像素点都进行同样的处理。 非自适应算法包括：最近邻，双线性，双三次，样条，sinc，lanczos等。 由于其复杂度, 这些插值的时候使用从0 to 256 (or more) 邻近像素。 包含越多的邻近像素，他们越精确，但是花费的时间也越长。这些算法可以用来扭曲和缩放照片。

2 Pytorch中能看到的插值方式

nn.Upsample()中的插值方式

出现的插值方式有

Nearest(最近邻插值法)，Linear(线性插值法)，Bilinear(双线性插值法)，Bicubic(双三次插值法)，Trilinear(三线性插值法)

3 Nearest插值法

3.1 方法介绍

顾名思义最近邻插值就是选取离目标点最近的点的值(黑点，原来就存在的点)作为新的插入点的值：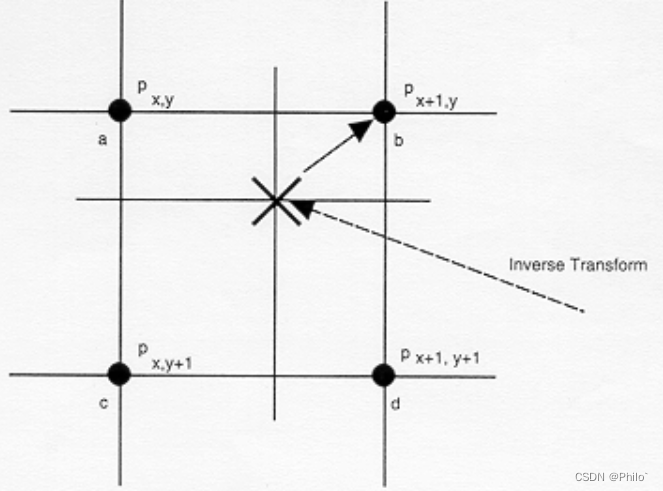

Pytorch代码演示：

可以看到在原始数据周围的点数据，其数值都是和其最近的点数值相同

3.2 优缺点

缺点： 由于是以最近的点作为新的插入点，因此边缘不会出现缓慢的渐慢过度区域，因而重新采样后灰度值有明显的不连续性，这也导致放大的图像容易出现锯齿的现象，缩小后的图像有很严重的失真；
优点： 最近邻插值法的优点是计算量很小，算法也简单，因此运算速度较快。

4 Linear插值法

4.1 方法接受

线性插值是以距离为权重的一种插值方式：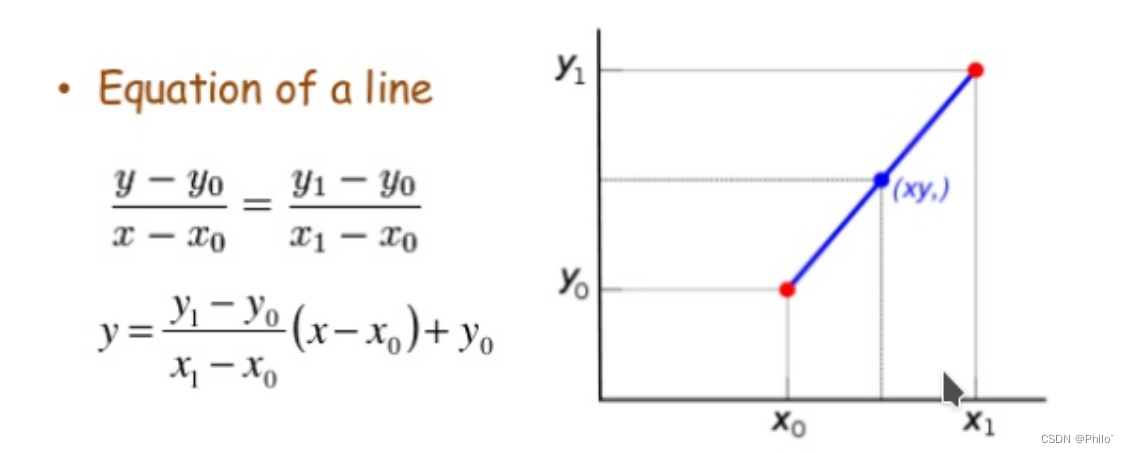

其本质就是利用两个点形成直线方程，带入x坐标，得到该像素点的插值。
Pytorch代码演示
由于在实际的代码中，需要给数据的每个点坐标附上像素值，在演示时不方便，因此后面会直接给出使用Upsample得到图象的例子。

4.2 优缺点

为的是给双线性插值法做铺垫的

5 Bilinear插值法

5.1 方法介绍

在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。见下图：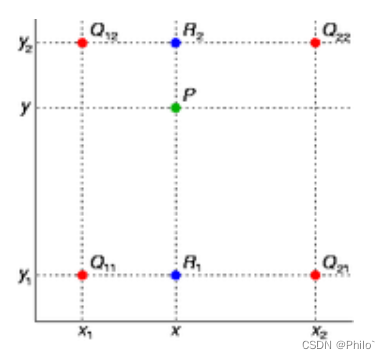

我们想得到未知函数 f 在点 P = (x, y) 的值，假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。最常见的情况，f就是一个像素点的像素值。思路是我们可以将求解过程分解为两次插值过程，首先在x轴方向上进行插值，根据点Q11,Q21得到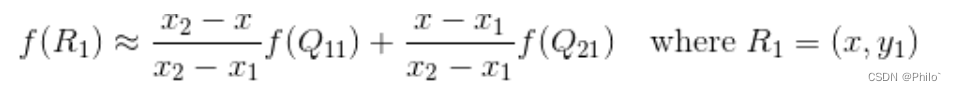

根据点Q12,Q22得到

然后在y轴方向上进行插值， 根据点R1 和R2得到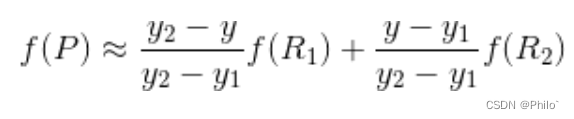

整理得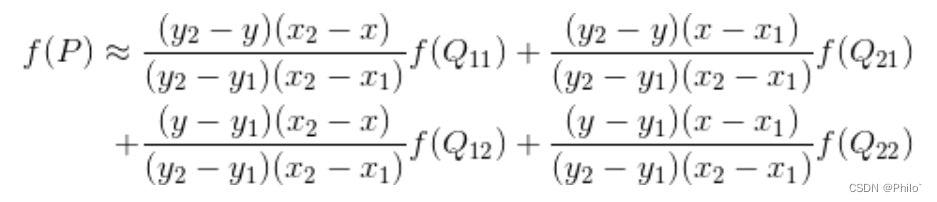

Pytorch代码演示：

5.2 优缺点

双线性插值利用周围四个邻点的灰度值在两个方向上做线性插值得到采样点的灰度值。这种方法在很大程度上消除了锯齿现象，但在边缘上变得较为模糊，同时需要一些计算量。

6 Bicubic插值法

6.1 方法介绍

太难了，有点没搞懂，可以参考末尾的参考博客！
Pytorch代码演示：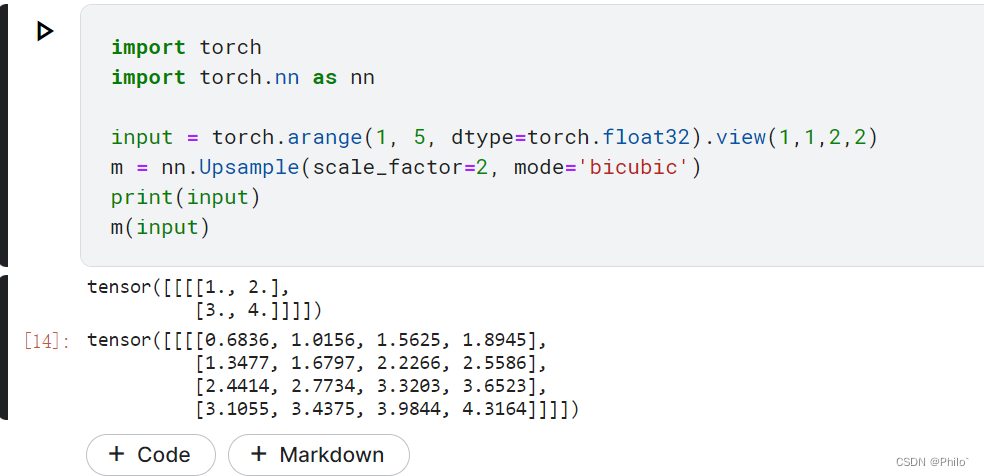

6.2 优缺点

双三次插值不仅考虑四个邻点灰度值，还考虑各邻点间的灰度值变化率的影响。是双线性插值的改进算法。和前两种经典插值方法相比，可以取得较好的插值效果。会损失插值图像的高频部分，因而是图像边缘模糊，需要的计算量也相应提升。

7 Trlinear插值法

7.1 方法介绍

就是在三维数据中，再使用一个坐标轴，和双线性插值法有异曲同工之处：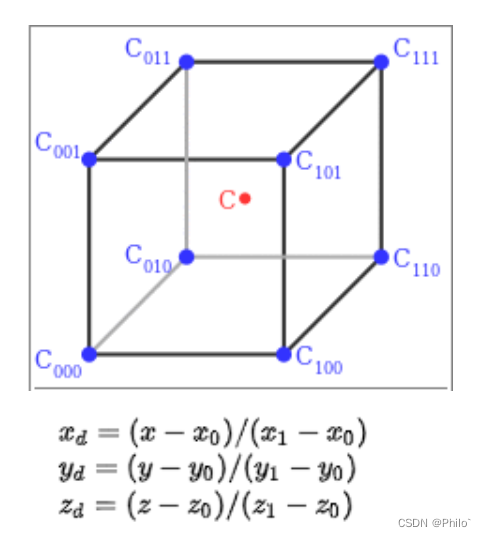

三线性插值的结果与沿三个轴的插值步骤的顺序无关：任何其他顺序，例如沿x，然后沿y，最后沿z，产生相同的值。

Pytorch代码演示：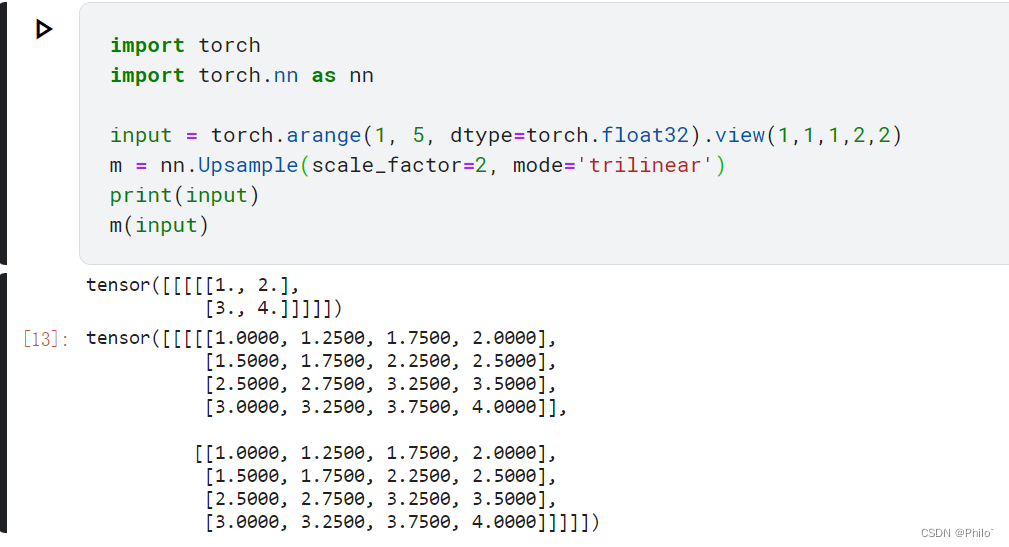

7.2 优缺点

就是双线性插值方法在高维数据中的应用是，是一个十分经典的算法！

8 图片演示

代码：

import torch
import torch.nn as nn
import torchvision.transforms as transforms 
import matplotlib.pyplot as plt

to_img = transforms.ToPILImage()input= torch.arange(64*64, dtype=torch.float32).view(1,1,64,64)
m_nearest = nn.Upsample(scale_factor=2, mode='nearest')
m_bilinear = nn.Upsample(scale_factor=2, mode='bilinear')
m_bicubic = nn.Upsample(scale_factor=2, mode='bicubic')
img_near = m_nearest(input)
img_bili = m_bilinear(input)
img_bicu = m_bicubic(input)

plt.subplot(2,2,1)
plt.title("Normal")
plt.imshow(to_img(input.squeeze(0).squeeze(0)), cmap="gray")

plt.subplot(2,2,2)
plt.title("Nearest")
plt.imshow(to_img(img_near.squeeze(0).squeeze(0)), cmap="gray")

plt.subplot(2,2,3)
plt.title("Bilinear")
plt.imshow(to_img(img_bili.squeeze(0).squeeze(0)), cmap="gray")

plt.subplot(2,2,4)
plt.title("Bicubic")
plt.imshow(to_img(img_bicu.squeeze(0).squeeze(0)), cmap="gray")
plt.show()

结果：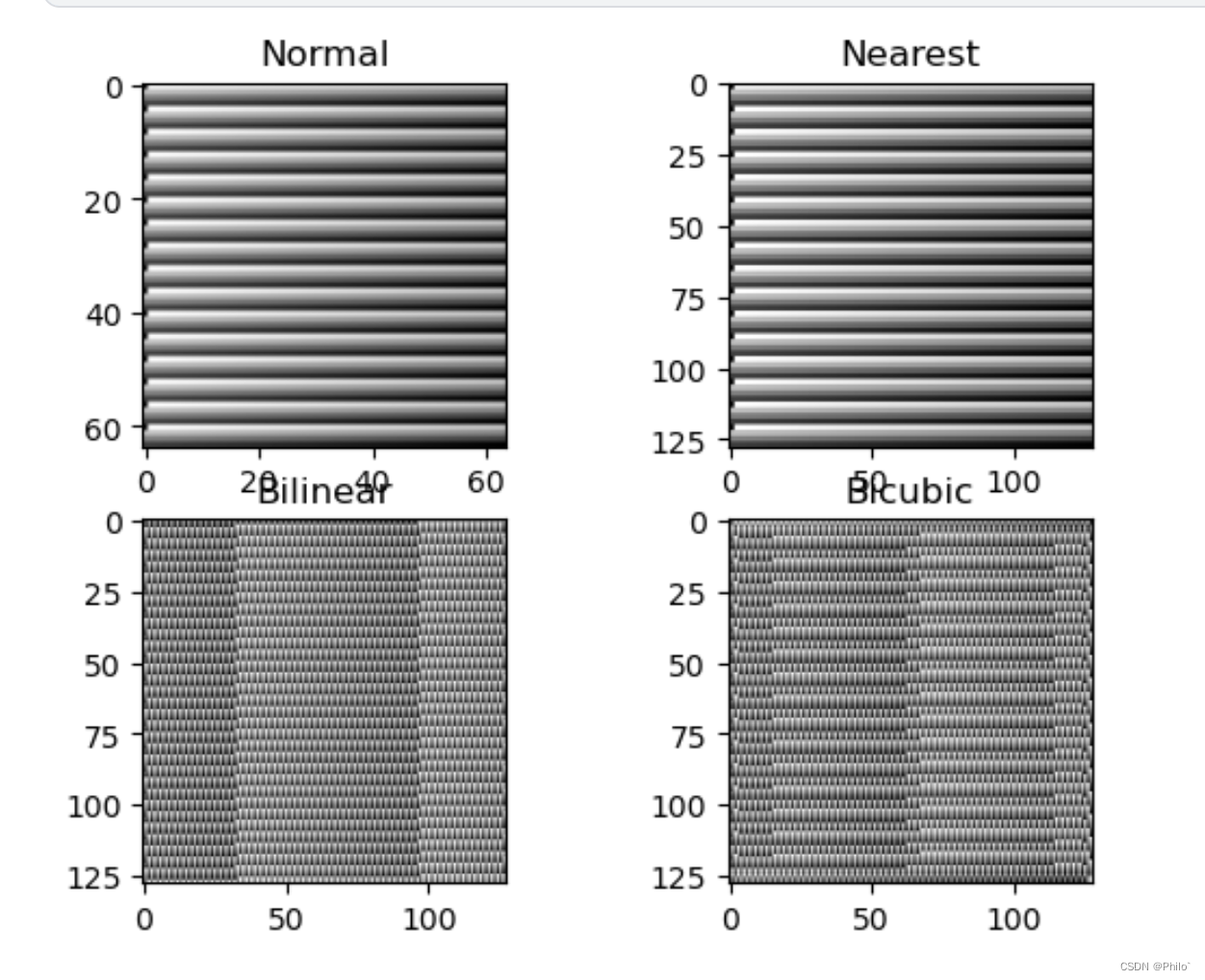

这个演示的稍显仓促，大家可以自己使用一张灰度图进行不同方式的插值放大，看看呈现出来的效果如何。

参考博客：

https://www.cnblogs.com/wxl845235800/p/7446270.html

https://www.cnblogs.com/laozhanghahaha/p/12580822.html

https://blog.csdn.net/weixin_42546737/article/details/110850247