文章目录
大家好我是秋刀鱼，今天给大家带来蓝桥杯题目题解。
打包
一行两个整数N和M。
一行N个整数，表示N个礼物的重量。输出格式
一个整数，表示最小的最大重量。
样例输入
3 2
1 1 2样例输出
2
数据规模和约定
N, M <= 100,000
重量 <= 1,000
题目解析
之前有写过：打包解析传送门🚀
约数个数
问题描述
我们用D(i)表示i有多少个约数。
例如 D(1)=1 D(2)=2 D(3)=2 D(4)=3。
给定n, 求D(1)+D(2)+D(3)+…+D(n)除以1000000007(10^9+7)的余数。输入格式
一个正整数n
输出格式
一行一个整数表示答案。
样例输入
4
样例输出
8
数据规模和约定
N<=10000000
解题思路
如果使用常规解法是会超时的，数据量太大仅允许时间复杂度
O
(
N
)
O(N)
O(N) 的算法。
可以换一种逻辑思考，既然已经知道了
n
n
n 的值，对于每一个数
i
i
i 能不能得到 1~n 中有多少个数拥有
i
i
i 这个约数呢？假设数量为
k
k
k ，结果值
a
n
s
+
=
k
ans+=k
ans+=k。
既然有
k
k
k 这个约数，那一定是：
k 2k 3k 4k 5k 6k ... nk
这些数能够拥有
k
k
k 余数，那么 1~n 中能整除
k
k
k 的数有多少呢？
答案是：
n
/
i
n/i
n/i ，也就是说拥有
i
i
i 这个约数的值数量为：
n
/
i
n/i
n/i ，因此遍历所有的
i
i
i 更新 ans 即使返回的答案
AC代码
#include<iostream>#include<math.h>
using namespace std;constint mod =1000000007;intmain(){int n;
cin >> n;long ans = n;int sq =sqrt(n);for(int i =2; i <= n;++i){
ans +=(n / i);
ans %= mod;}
cout << ans;return0;}
第二点五个不高兴的小明
问题描述
有一条长为n的走廊，小明站在走廊的一端，每次可以跳过不超过p格，每格都有一个权值wi。
小明要从一端跳到另一端，不能回跳，正好跳t次，请问他跳过的方格的权值和最大是多少？输入格式
输入的第一行包含两个整数n, p, t，表示走廊的长度，小明每次跳跃的最长距离和小明跳的次数。
接下来n个整数，表示走廊每个位置的权值。输出格式
输出一个整数。表示小明跳过的方格的权值和的最大值。
样例输入
8 5 3
3 4 -1 -100 1 8 7 6样例输出
12
数据规模和约定
1<=n, p, t<=1000, -1000<=wi<=1000。
解题思路
这道题核心思路是动态规划，定义状态
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j]。
假设格的下标开始为1，那么
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 存储"小明跳跃到第
i
i
i 格且最多还有
j
j
j 次跳跃机会" 状态下的跳过方格的最大权值。
状态转移方程
对于
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 的状态。假设小明跳跃的最长距离为
p
p
p , 如果跳跃到
i
i
i 格，一定是从
[
i
−
p
,
i
]
[i-p,i]
[i−p,i] 中的一个格子跳跃，将之前跳跃的这个格子视为过去状态。那么
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 一定是所有过去状态的最大值，也就是能一步跳跃到
i
i
i 点且剩余步数为
j
+
1
j+1
j+1 时状态的最大值，即：
d
p
[
i
]
[
j
]
=
m
a
x
(
d
p
[
i
−
1
]
[
j
+
1
]
,
d
p
[
i
−
2
]
[
j
+
1
]
.
.
.
d
p
[
i
−
p
]
[
j
+
1
]
)
+
a
r
r
[
i
]
dp[i][j]=max(dp[i-1][j+1],dp[i-2][j+1]...dp[i-p][j+1])+arr[i]
dp[i][j]=max(dp[i−1][j+1],dp[i−2][j+1]...dp[i−p][j+1])+arr[i]，也就是说当前的状态一定能通过之前的状态推导而来。
例如
p
=
3
p=3
p=3 ，
d
p
[
5
]
[
3
]
dp[5][3]
dp[5][3] =
m
a
x
(
d
p
[
4
]
[
4
]
,
d
p
[
3
]
[
4
]
,
d
p
[
2
]
[
4
]
)
+
a
r
r
[
5
]
max(dp[4][4],dp[3][4],dp[2][4])+arr[5]
max(dp[4][4],dp[3][4],dp[2][4])+arr[5]
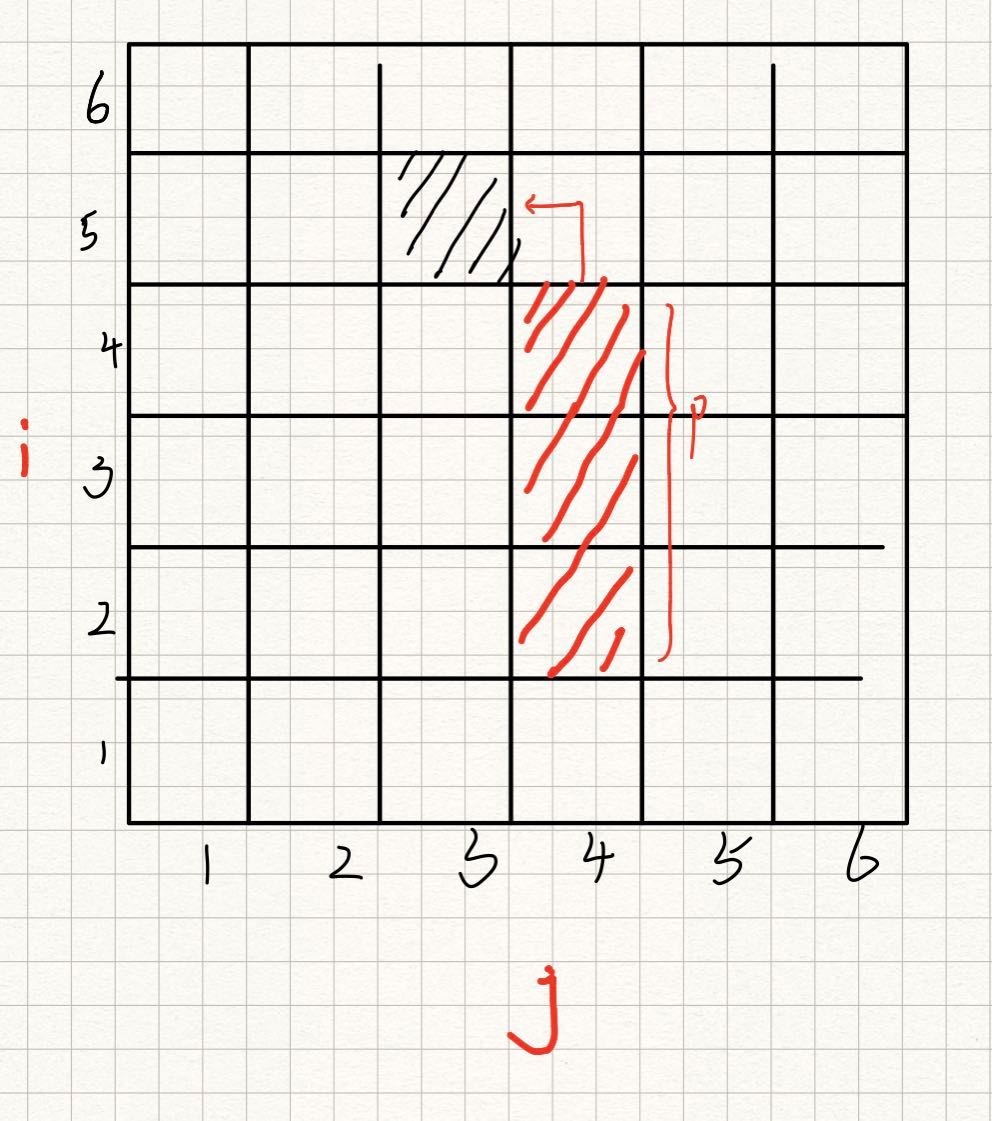
状态初始化
为了开始时所有状态都设置为给定的一个极小值，同时将第一次跳跃能够到达的格子
i
i
i 预先处理，即：
d
p
[
i
]
[
t
−
1
]
=
a
r
r
[
i
]
dp[i][t-1] =arr[i]
dp[i][t−1]=arr[i]
得到结果
最终得到的
d
p
dp
dp 数组中 ,
d
p
[
n
+
1
]
[
t
]
dp[n+1][t]
dp[n+1][t] 就是返回的结果
AC代码
#include<iostream>#include<string.h>#include<math.h>#include<vector>#include<algorithm>#include<set>#include<stack>#include<map>#include<queue>#include<deque>
using namespace std;#define ll long long#define M 1010#define M_MIN -1000000
using namespace std;int arr[M];
ll dp[M][M];intmain(){int n, p, t;
cin >> n >> p >> t;for(int i =1; i <= n; i++){
cin >> arr[i];}// 初始化memset(dp,0,sizeof(dp));for(int i =0; i < M;++i){for(int j =0; j < M;++j){
dp[i][j]= M_MIN;}}// 处理一次跳跃的情况for(int i =1; i <= n +1&& i <= p; i++){
dp[i][t -1]= arr[i];}// 对于每一格for(int i =2; i <= n +1; i++){for(int j =0; j <= t; j++){// 寻找最大值，注意边界处理for(int k =1; k <= p && k < i; k++){
dp[i][j]=max(dp[i][j], dp[i - k][j +1]+ arr[i]);}}}
cout << dp[n +1][0];return0;}
代码优化
其实开始做这道题时我以为上面的代码可能会超时，因为时间复杂度接近
O
(
n
3
)
O(n^3)
O(n3) （然而并没有）。时间复杂度之所以这么高是因为在遍历
d
p
dp
dp 中每一个元素过程中，每次的遍历都会带来至多
p
p
p 次的额外运算，目的是为了寻找最大值，但其实大部分的运算都是重复运算，浪费了很多时间。
还是拿这个例子举例：
红色部分对应的是
i
=
5
,
j
=
3
i=5,j=3
i=5,j=3 时，需要搜索的元素。那如果是
i
=
6
,
j
=
3
i=6,j=3
i=6,j=3 的情况呢？如下图所示：
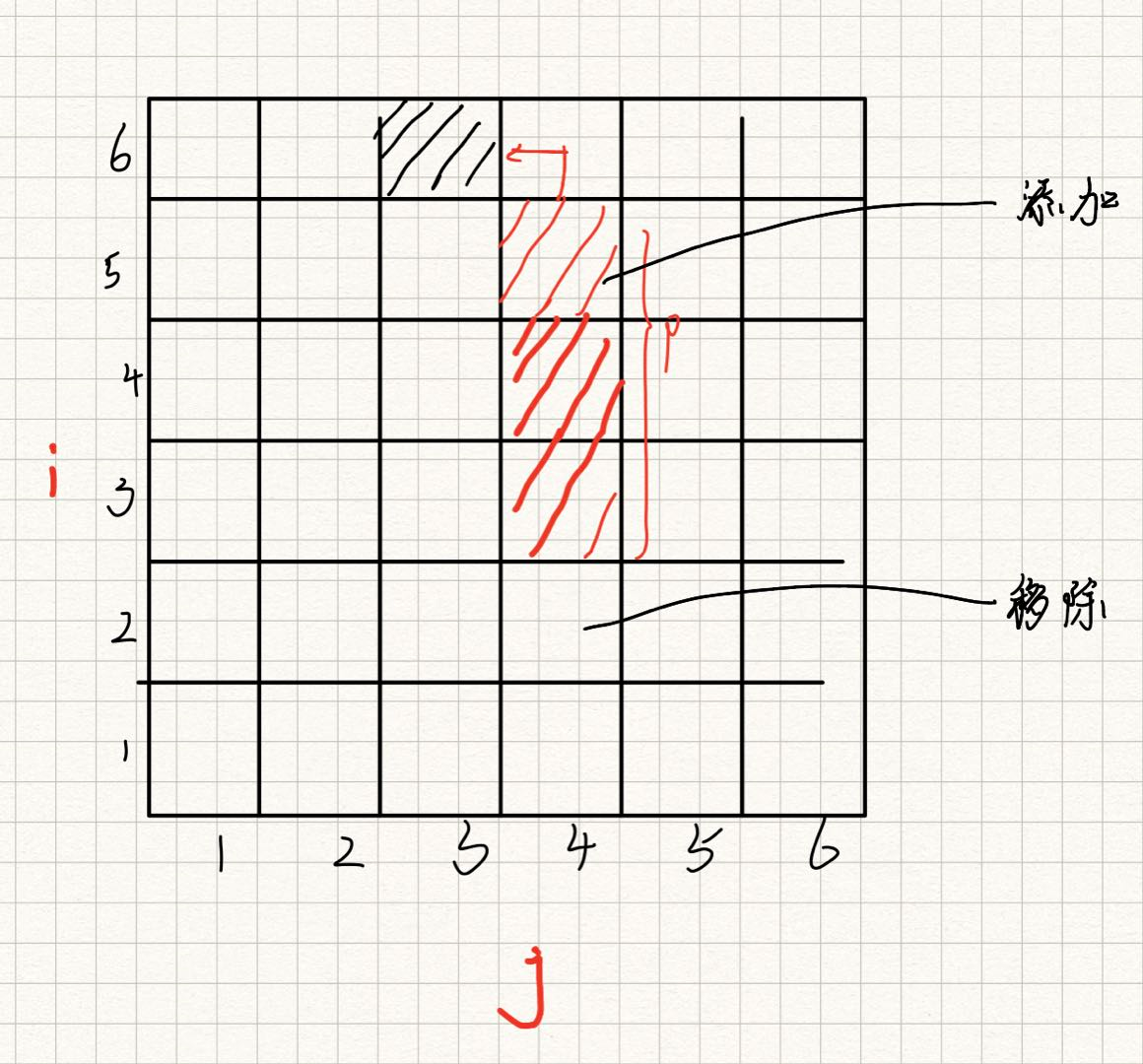不难发现，因为至多搜索数量p个元素，且开始位置固定，所以原本的 dp[2][4] 元素被剔除，添加了新的搜索元素 dp[5][4] 。 每次添加最近的元素，删除最远的元素，这种搜索逻辑像极了队列。
如果我们能够实现一种数据结构，在实现队列添加、删除元素的基础上，能够在接近
O
(
1
)
O(1)
O(1) 的时间复杂度下获取到队列中的最大元素，本题目就能够优化。
数据结构实现
为了实现这个数据结构，定义了一个队列
q
u
1
qu1
qu1 存放所有元素，定义队列
q
u
2
qu2
qu2 存放大小关系，保证先加入的元素如果小于后加入的元素，先加入的元素会被移除队列，且
q
u
2.
b
a
c
k
(
)
qu2.back()
qu2.back() 存储
q
u
1
qu1
qu1 队列中最大的元素。
struct maxQueue {// 存储所有元素
queue<ll>qu1;// 队列末尾存放最大元素
deque<ll>qu2;// push 方法的实现voidupdate(int val){// 如果队列中元素个数超过p，移除最开始加入的元素if(qu1.size()== p){
this->pop();}// 添加元素
qu1.push(val);while(!qu2.empty()&& qu2.back()< val){
qu2.pop_back();}
qu2.push_back(val);}intmax(){return qu2.empty()? M_MIN : qu2.front();}
private:voidpop(){if(qu2.front()== qu1.front()){
qu2.pop_front();}
qu1.pop();}// 每一列对应的数值队列}maxStack[M];
逻辑实现
现在还是预先处理一步到达格子的状态，即
d
p
[
i
]
[
t
−
1
]
=
a
r
r
[
i
]
dp[i][t-1]=arr[i]
dp[i][t−1]=arr[i]
在遍历
d
p
dp
dp 数组的第
i
i
i 行之前，首先将
i
−
1
i-1
i−1 行的数组更新到队列中，随后开始遍历第
i
i
i 行更新状态，其余代码与前面的方法相似。
AC代码2
#include<iostream>#include<string.h>#include<math.h>#include<vector>#include<algorithm>#include<set>#include<stack>#include<map>#include<queue>#include<deque>#define ll long long
using namespace std;#define M 1010#define M_MIN -1000000int n, p, t;int arr[M];int dp[M][M];struct maxQueue {// 存储所有元素
queue<ll>qu1;// 队列末尾存放最大元素
deque<ll>qu2;// push 方法的实现voidupdate(int val){// 如果队列中元素个数超过p，移除最开始加入的元素if(qu1.size()== p){
this->pop();}// 添加元素
qu1.push(val);while(!qu2.empty()&& qu2.back()< val){
qu2.pop_back();}
qu2.push_back(val);}intmax(){return qu2.empty()? M_MIN : qu2.front();}
private:voidpop(){if(qu2.front()== qu1.front()){
qu2.pop_front();}
qu1.pop();}}maxStack[M];intmain(){memset(arr,0,sizeof(M));memset(dp,0,sizeof(dp));
cin >> n >> p >> t;// 初始化for(int i =0; i <= n;++i){for(int j =0; j <= n;++j){
dp[i][j]= M_MIN;}}for(int i =1; i <= n;++i){
cin >> arr[i];}for(int i =1; i <= p && i <= n;++i){
dp[i][t -1]= arr[i];}for(int i =2; i <= n +1;++i){// 更新上一行的状态到队列中，注意对应位置for(int j =0; j <= t -1;++j){
maxStack[j].update(dp[i -1][j +1]);}// 修改 i 行状态for(int j = t -2; j >=0;--j){
dp[i][j]= maxStack[j].max()+ arr[i];}}
cout << dp[n +1][0];return0;}
总结
上面是两种方法的耗时情况比较，其中第二行数据是未优化的代码，第一行的数据时优化后的代码。时间复杂度从
O
(
n
3
)
O(n^3)
O(n3) 降为接近
O
(
n
2
)
O(n^2)
O(n2) ，效果也是相当的明显，非常好用！
写在最后
代码、论述中有任何问题，欢迎大家指出，同时如果有任何疑问，也能够在评论区中留言，大家共同讨论共同进步！
如果觉得博主写的不错的话，可以点赞支持一下！
本文转载自: https://blog.csdn.net/qq_51439643/article/details/123849426
版权归原作者 秋刀鱼与 猫 所有， 如有侵权，请联系我们删除。
版权归原作者 秋刀鱼与 猫 所有， 如有侵权，请联系我们删除。