二叉树非递归遍历

个人主页：熬夜磕代码丶
作品专栏: 数据结构与算法
我变秃了，也变强了
给大家介绍一款程序员必备刷题平台——牛客网
点击注册一起刷题收获大厂offer吧

文章目录

一、二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历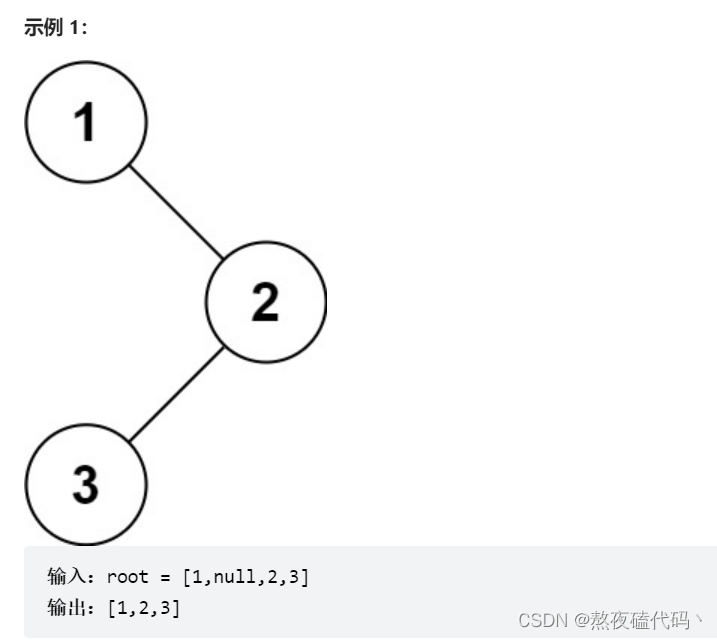

思路分析：
定义一个cur结点去遍历左子树，每遍历一个结点就将它放入栈中并且打印，直到左子树为空时。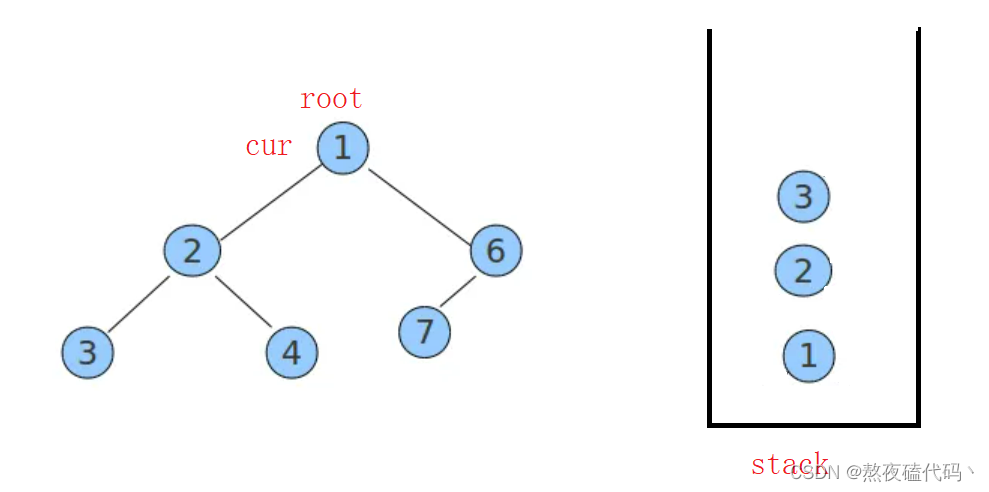

从栈中弹出一个元素top,cur指向top的右子树.直到cur为空并且栈也为空时便不在循环。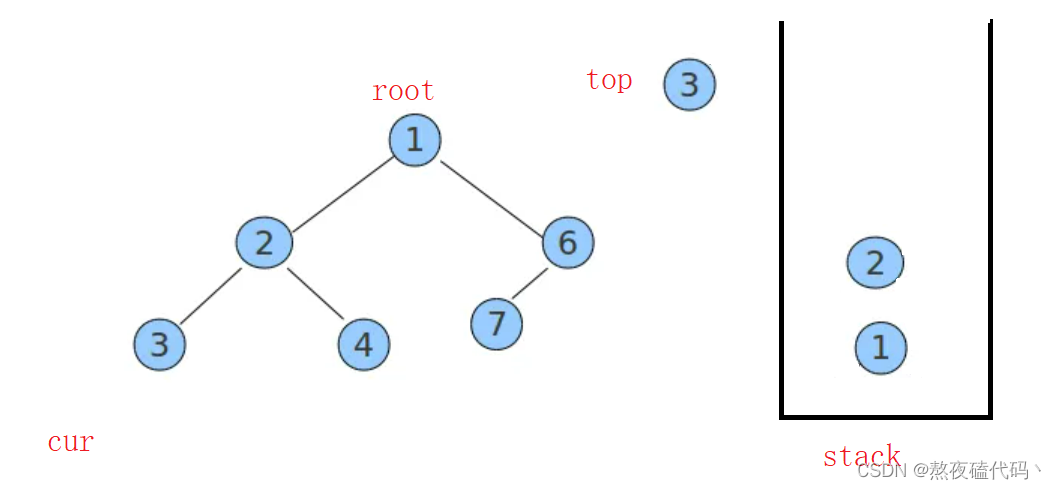

publicList<Integer>preorderTraversal(TreeNode root){List<Integer> list =newArrayList<>();Stack<TreeNode> stack =newStack<>();TreeNode cur = root;while(cur !=null||!stack.isEmpty()){while(cur !=null){
                stack.push(cur);
                list.add(cur.val);
                cur = cur.left;}TreeNode top = stack.pop();
            cur = top.right;}return list;}

二、二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。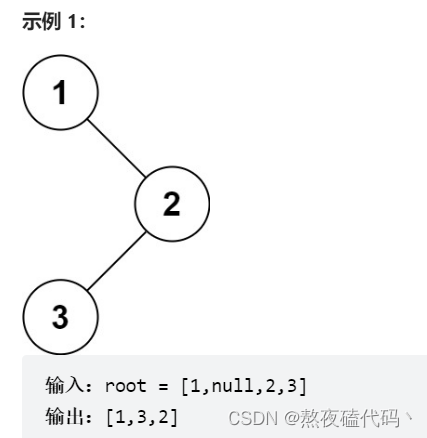

思路分析：
中序遍历与前序遍历思路大致相同，都是定义一个cur结点去遍历二叉树，不过中序遍历是一直将左子树放入stack中，直到左子树为空。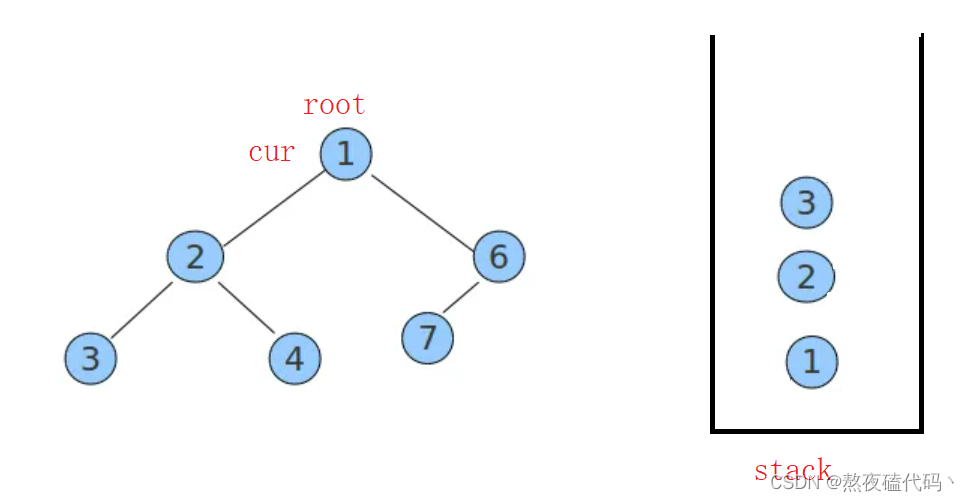

当左子树为空时，从stack中弹出一个结点，然后打印该节点，使cur指向top的右节点，直到cur为空并且栈也为空时便不在循环。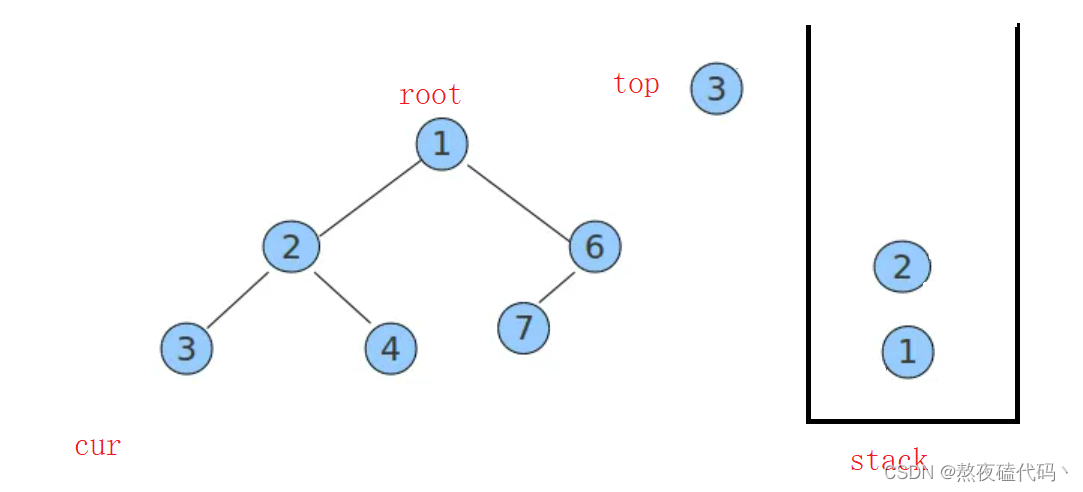

publicList<Integer>inorderTraversal(TreeNode root){List<Integer> list =newArrayList<>();Stack<TreeNode> stack =newStack<>();TreeNode cur = root;while(cur !=null||!stack.isEmpty()){while(cur !=null){
                stack.push(cur);
                cur = cur.left;}TreeNode top = stack.pop();
            list.add(top.val);
            cur = top.right;}return list;}

三、二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。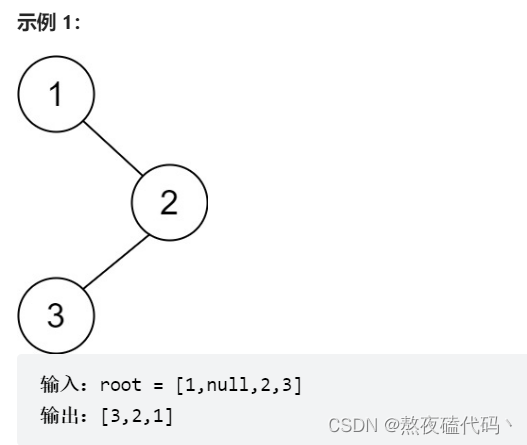

思路分析：
后序遍历同样的，遍历二叉树，将每一个结点放入stack中，直到左子树为空时。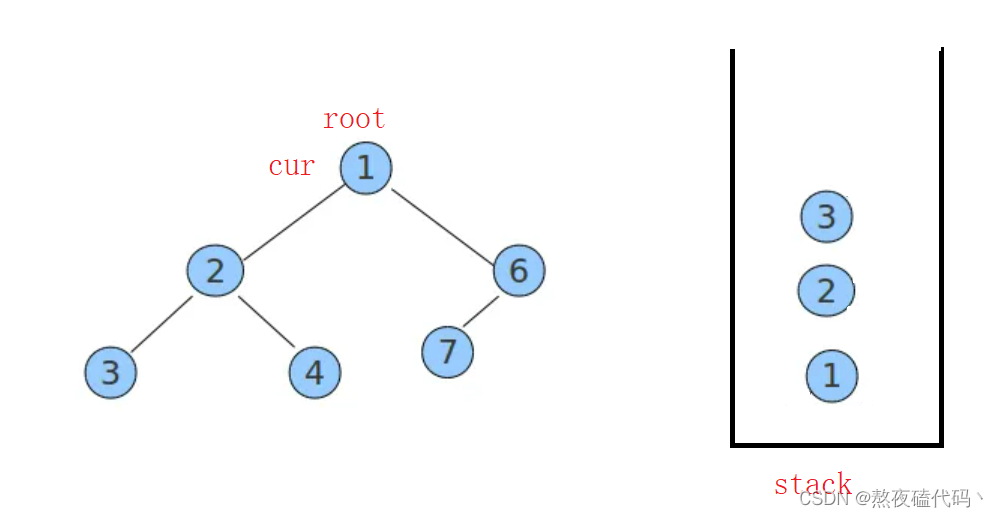

需要注意的是我们不是直接弹出栈，而是peek一下栈顶元素，这里我们就要分情况讨论了top的右子树是否为空，如果为空直接打印top元素，并且弹出，如果不为空那么使用cur指向top的右子树。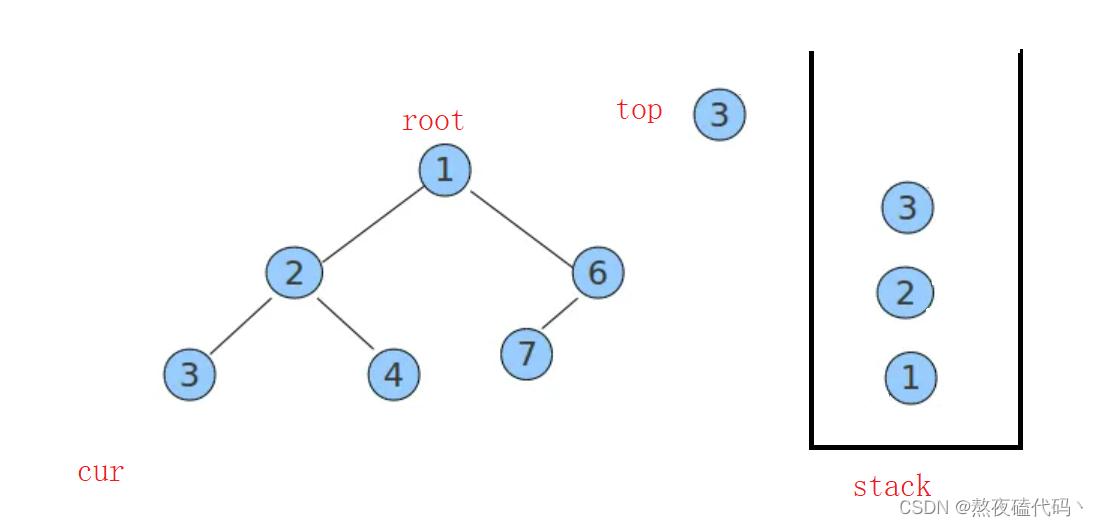
但这样我们的程序会出现一个bug，我们使cur指向top右节点后，将cur打印弹出后。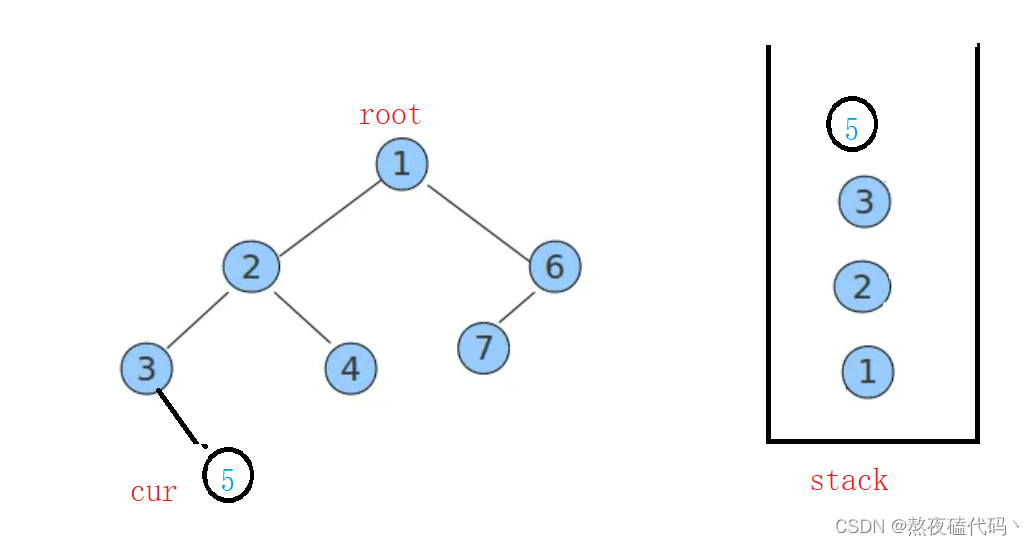
我们会发现程序又会使cur指向top右节点，这样无止的循环。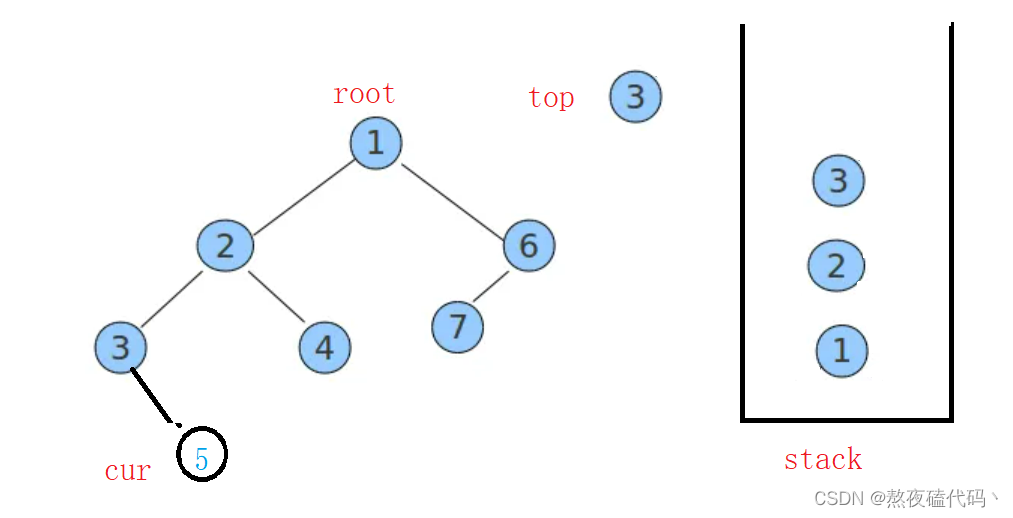

所以我们定义一个pre变量，prev用来定义上一次打印的结点，如果top的的右节点与prev结点相同时将不再遍历右节点，而直接打印top结点，并且stack弹出元素。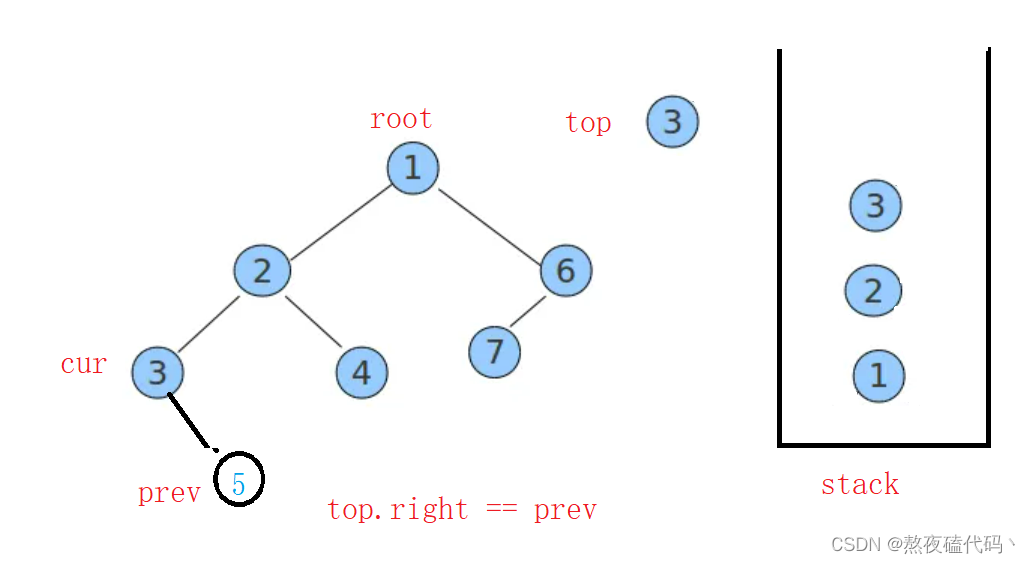

publicList<Integer>postorderTraversal(TreeNode root){List<Integer> list =newArrayList<>();Stack<TreeNode> stack =newStack<>();TreeNode cur = root;TreeNode prev =null;while(cur !=null||!stack.isEmpty()){while(cur !=null){
                stack.push(cur);
                cur = cur.left;}TreeNode top = stack.peek();if(top.right ==null|| top.right == prev){
                list.add(top.val);
                stack.pop();
                prev = top;}else{
                cur = top.right;}}return list;}

四、从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。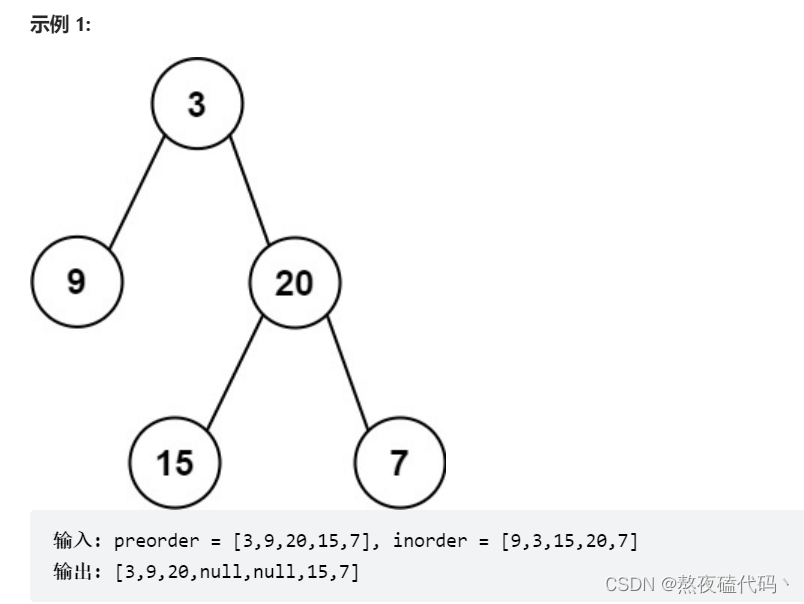

思路分析：
这里我们随便给一颗二叉树分析一下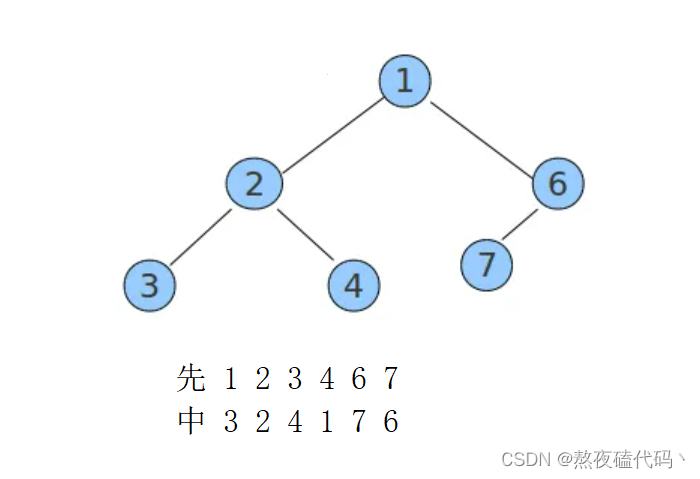

我们遍历从前往后遍历先序数组，第一位就是二叉树的根节点，然后在中序遍历中找到该结点，该节点为分界线，该节点的左边的就是根节点的左子树，右边的就是右子树。

然后去构建根节点的左子树，遍历先序数组，然后在中序数组中找到该结点，左边的就是左子树，右边的就是右子树。

我们可以发现安装这个思路可以将二叉树构建出来，但是我们需要考虑一些条件，什么条件的时候，应该停止，首先中序遍历的数组的left应该小于right，还有得保证中序遍历中找到先序遍历的元素，否则返回-1下标，停止递归。

publicint pre =0;publicTreeNodebuildTree(int[] preorder,int[] inorder){returnsortTree(preorder,inorder,0,inorder.length -1);}publicTreeNodesortTree(int[] preorder,int[] inorder,int left,int right){//1.判断是否还有左右子树if(left > right){returnnull;}TreeNode root =newTreeNode(preorder[pre]);int index =findIndex(inorder,left,right,preorder[pre]);if(index ==-1){returnnull;}
        pre++;
        root.left =sortTree(preorder,inorder,left,index -1);
        root.right =sortTree(preorder,inorder,index +1,right);return root;}publicintfindIndex(int[] inorder,int left,int right,int val){if(left > right){return-1;}for(int i = left; i <= right; i++){if(inorder[i]== val){return i;}}return-1;}

五、从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。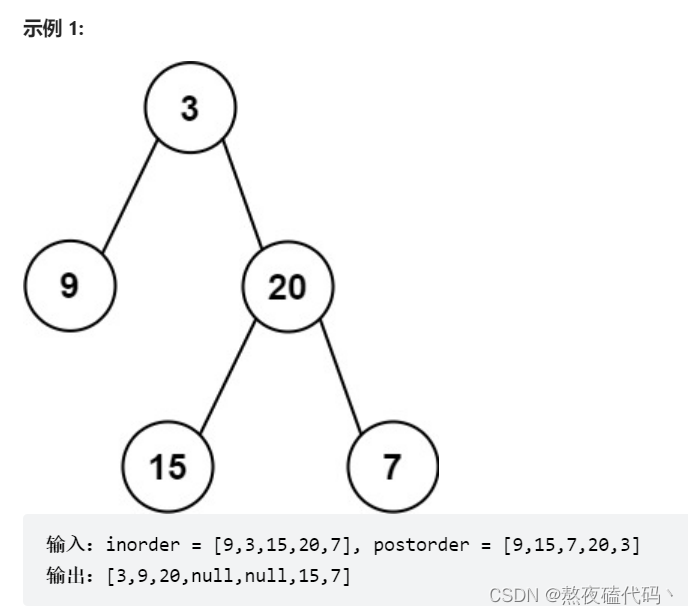

思路分析：
这里我们随便给一颗二叉树分析一下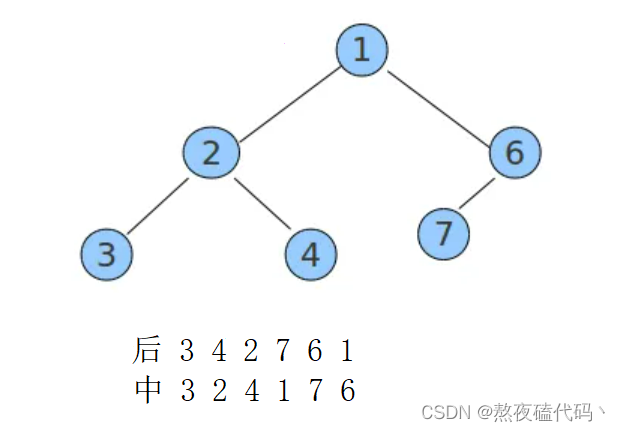

这次我们从后往前遍历后序数组，每遍历的一位都为该子树的根节点，不过我们得先遍历右子树，因为后序遍历的顺序是左子树-》右子树-》根节点，我们从后往前遍历后序数组，相当于反着来。中序遍历找到先序遍历的元素，左边的为左子树，右边的为右子树。

我们可以发现安装这个思路可以将二叉树构建出来，但是我们需要考虑一些条件，什么条件的时候，应该停止，首先中序遍历的数组的left应该小于right，还有得保证中序遍历中找到先序遍历的元素，否则返回-1下标，停止递归。
而且我们定义后序数组遍历下标时，因为我们是从后往前遍历，所以我们应定义为数组大小-1.

publicint last =0;publicTreeNodebuildTree(int[] inorder,int[] postorder){
        last = inorder.length -1;returnsortTree1(postorder,inorder,0,inorder.length -1);}publicTreeNodesortTree1(int[] postorder,int[] inorder,int left,int right){//1.判断是否还有左右子树if(left > right){returnnull;}//找到中序遍历位置TreeNode root =newTreeNode(postorder[last]);int index =findIndex1(inorder,left,right,postorder[last]);if(index ==-1){returnnull;}
        last--;//构建左右子树
        root.right =sortTree1(postorder,inorder,index +1,right);
        root.left =sortTree1(postorder,inorder,left,index -1);return root;}publicintfindIndex1(int[] inorder,int left,int right,int val){if(left > right){return-1;}for(int i = left; i <= right; i++){if(inorder[i]== val){return i;}}return-1;}

六、根据二叉树创建字符串

给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。
空节点使用一对空括号对 “()” 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。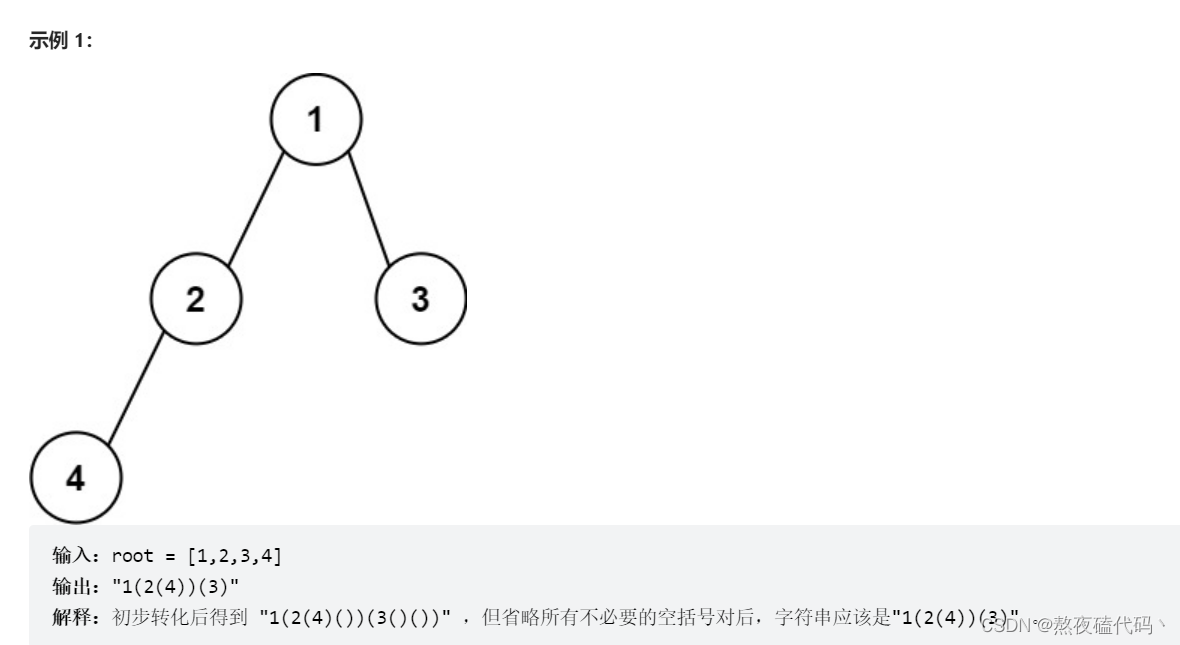

思路分析：
按照题目的大意，就是先序二叉树，在有些情况下加入( 或者 ),我们来具体分析下什么情况下应该加什么。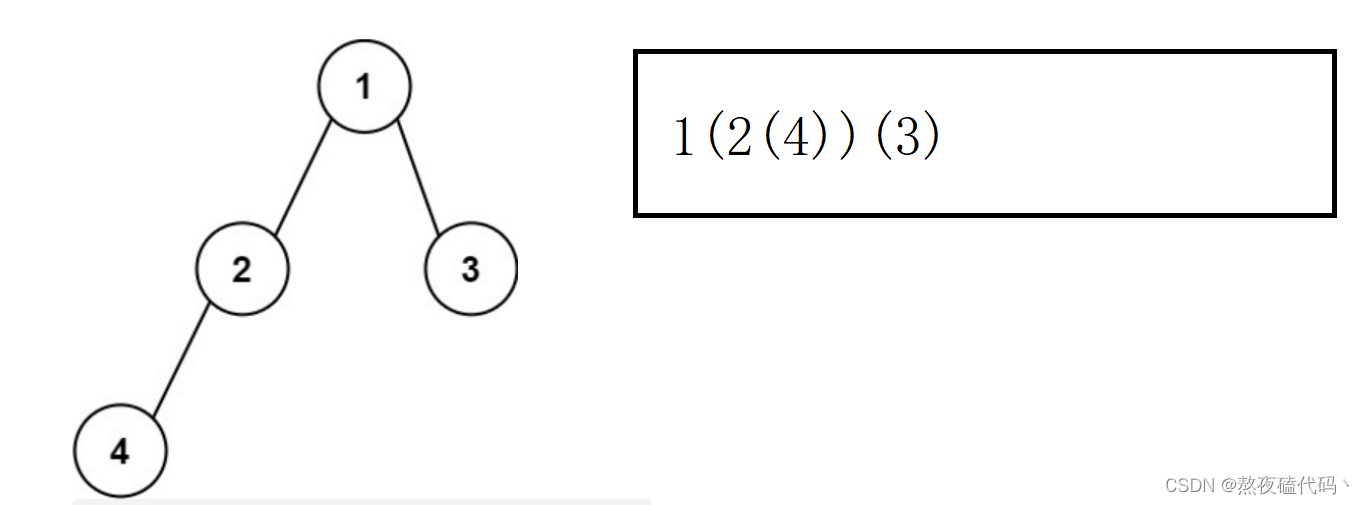

我们可以发现，根节点不用加任何括号，在遍历其他任何结点时加一个 ( 返回该节点时加一个 ），但还有一些边界条件需要判断一下。我们发现当左子树为空时，右子树不为空时，得加一个完整的括号，不然会破坏一一映射关系。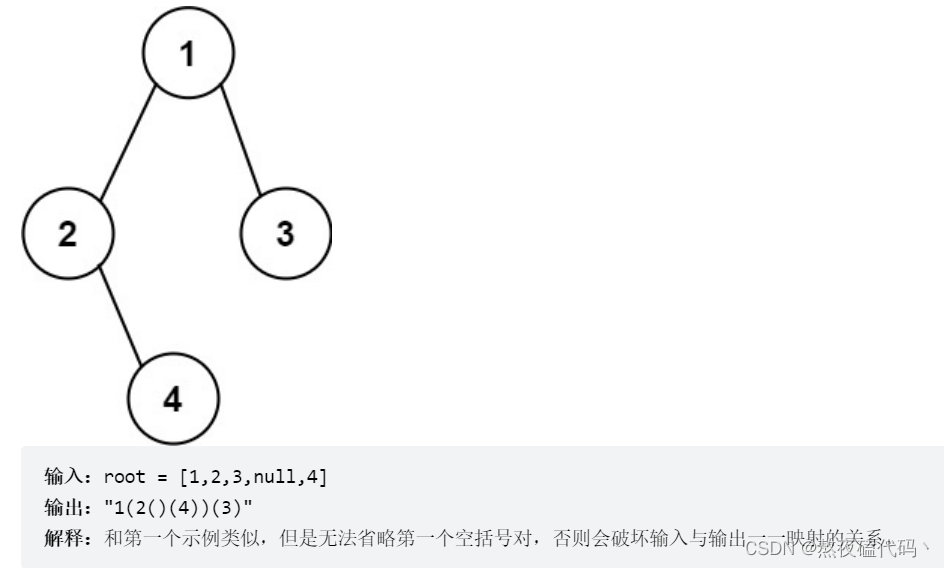

还有一点就是我们不断地拼接字符串，所以我们使用StringBuilder对象去拼接，然后toString,不然会创建大量String对象浪费空间。

publicStringtree2str(TreeNode root){StringBuilder sb =newStringBuilder();treeToStr(root,sb);return sb.toString();}publicvoidtreeToStr(TreeNode root,StringBuilder sb){if(root ==null){return;}
        sb.append(root.val);if(root.left !=null){
            sb.append("(");treeToStr(root.left,sb);
            sb.append(")");}else{if(root.right ==null){return;}else{
                sb.append("()");}}if(root.right ==null){return;}else{
            sb.append("(");treeToStr(root.right,sb);
            sb.append(")");}}