⏰诗赋清音:墨激雷霆势,心随碧波飘。山河承豪情滔天,梦御风云志浩荡。
** 🎉欢迎大家关注🔍点赞👍收藏⭐️留言📝**
🔔****作者留言:欢迎来到我的【SQL Server】魔法学堂!这里是探索数据库世界的秘境,我的学习笔记博客为你打开SQL Server的魔法之门。在这里,我不仅分享SQL Server的基础知识和高级技巧,还有着涉猎实用技术和项目经验的魔法药水。无论你是新手还是数据库巫师,这个魔法堂会为你施展出奇幻的学习魔法,帮助你在SQL Server的魔法森林中踏上一场奇妙之旅。准备好了吗?跟着我,让我们一起编织属于自己的SQL Server魔法代码!
🌌第二章 关系数据库
🌍1. 关系数据结构及形式化定
🪐1.1 关系
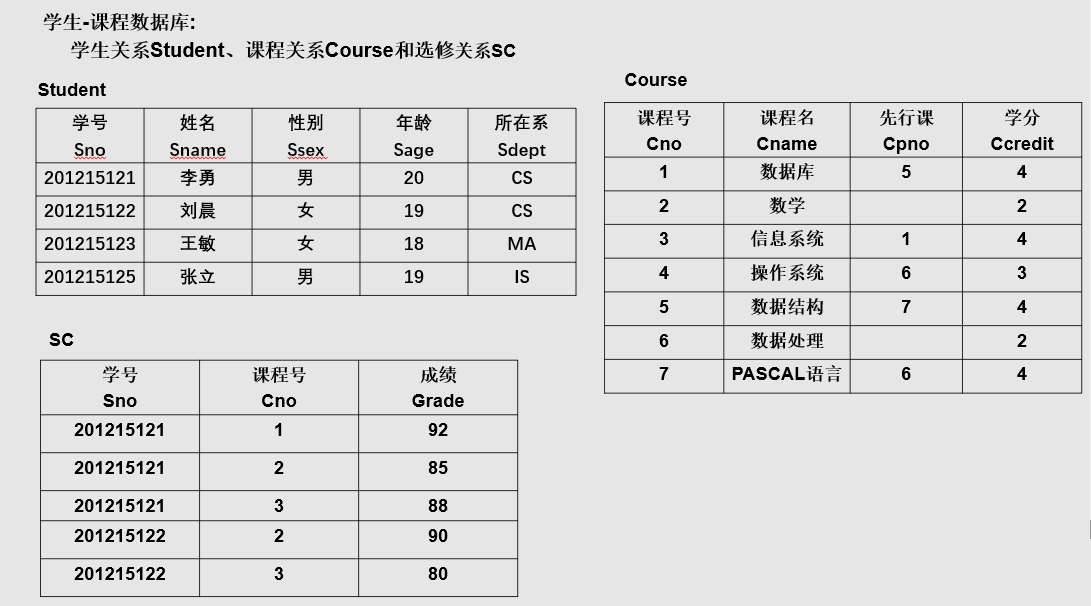
关系模型的数据结构:关系【二维表】
1. 域:相同数据结构值的集合,如sex属于域:{“男”,“女”}2. 笛卡儿积:域运算
示例:
给出3个域:
D1={a1,a2}
D2={b1,b2}
D3={c1,c2,c3}
D1,D2,D3的笛卡尔积为D1×D2×D3={
(a1,b1,c1),(a1,b1,c2),(a1,b1,c3), (a1,b2,c1), (a1,b2,c2),(a1,b2,c3), (a2,b1,c1),(a2,b1,c2),(a2,b1,c3), (a2,b2,c1),(a2,b2,c2),(a2,b2,c3) }元组:(a1,b1,c1)...
分量:a1...
基数为2×2×3=12
笛卡尔积的定义:
给定一组域D1,D2,…,Dn,允许其中某些域是相同的。
** D1×D2×…×Dn ={(d1,d2,…,dn)|di∈Di,i=1,2,…,n}**域的所有取值的一个组合不重复
元组:笛卡尔积中每一个元素(d1,d2,…,dn)叫作一个n元组(n-tuple)或简称元组分量:笛卡尔积元素(d1,d2,…,dn)中的每一个值di 叫作一个分量
基数:Di(i=1,2,…,n)为有限集,其基数为mi(i=1,2,…,n),则D1×D2×…×Dn
的基数M为:
表示方法:一张二维表,行对应元组,列对应属性【域】
3. 关系
定义:
D1×D2×…×Dn的子集叫作在域D1,D2,…,Dn上的关系,表示为**R(D1,D2,…,Dn)** * R:关系名,n:关系的目或度*当n=1时,称该关系为一元关系
当n=2时,称该关系为二元关系...
相关概念
- 元组:关系中的每个元素
- 候选码:若关系中的某一属性组的值能唯一地标识一个元组
- 全码:所有属性组是候选码
- 主码:若一个关系有多个候选码,则选定其中一个为主码
- 主属性:候选码的诸属性称为主属性
- 非主属性:不包含在任何侯选码中的属性
关系的三种类型:
- 基本表【基本关系】:实际存在的表
- 查询表:查询结果对应的表
- 视图表:由基本表或其他视图表导出的表,是虚表
基本关系性质:
- 列同质不同名
- 行列无序
- 键值唯一不为空
- 分量不可分
🪐1.2 关系模式
关系模式是型、关系是值,关系模式是对关系的描述
关系模式的表示:
R(U,D,DOM,F)
R 关系名
U 组成该关系的属性名集合
D U中属性所来自的域
DOM 属性向域的映象集合
F 属性间数据的依赖关系的集合
关系模式和关系的区别
- 关系模式是对关系的描述,是静态的、稳定的
- 关系是关系模式在某一时刻的状态或内容,是动态的、随时间不断变化的
注意:
- 关系是元组的集合,由主码唯一标识。
- 关系模型的逻辑结构是表,物理结构交给OS完成。
🌍2. 关系操作
常用的关系操作【集合操作】
- 查询操作:选择、投影、连接、除、并、差、交、笛卡尔积,其中选择、投影、并、差、笛卡尔基是5种基本操作
- 数据更新:插入、删除、修改
🌍3. 关系的完整性
三类完整性约束:
- 实体完整性:键值唯一不为空示例:选修(学号,课程号,成绩) “学号、课程号”为主码,则“学号”和“课程号”两个属性都不能取空值
- 参照完整性:定义外码与主码使用规则示例:学生(学号,姓名,性别,专业号,年龄)专业(专业号,专业名)专业号是专业的主码,但不是学生的主码,并且专业号与学号相对应,则专业号是学生的外码。
- 用户定义的完整性:如某值不能为空,某值唯一,sex范围限制为{"男","女"}...
🌍4. 关系代数
运 算 符
含 义
传统的
运算符
∪
并
-
差
∩
交
×
笛卡尔积
专门的
运算符
σ
选择
π
投影
连接
÷
除
🪐4.1 传统的运算符
🌕**1. 并 **U
R∪S 仍为n目关系,由属于R或属于S的元组组成 R∪S = { t|t ∈ R∨t ∈S }
🌕2. 差 -
R - S 仍为n目关系,由属于R而不属于S的所有元组组成 R -S = { t|t∈R∧t∈S }
🌕**3. 交 **∩
R∩S仍为n目关系,由既属于R又属于S的元组组成 R∩S = { t|t ∈R∧t ∈S }
【R∩S = R –(R-S)】
🌕4. 笛卡尔积 R×S
R×S
列:(n+m)列元组的集合,元组的前n列是关系R的一个元组,后m列是关系S的一个元组
行:k1×k2个元组 ** R×S = {tr ts |tr ∈R ∧ ts∈S }**
🪐4.2 专门的运算符
基本概念:
设关系模式为R(A1,A2,…,An),它的一个关系设为R
- **t∈R **表示t是R的一个元组
- **t[Ai] **则表示元组t中相应于属性Ai的一个分量
**象集 **
则
- x1在R中的象集 Zx1 ={Z1,Z2,Z3}
- x2在R中的象集 Zx2 ={Z2,Z3}
- x3在R中的象集 Zx3 ={Z1,Z3}
🌕**1. 选择 **σ
在关系R中选择满足给定条件的诸元组 σF(R) = {t|t∈R∧F(t)= '真'}
示例:
查询信息系(IS系)全体学生。
σSdept = 'IS' (Student)Sno
Sname
Ssex
Sage
Sdept
201215125
张立
男
19
IS
查询年龄小于20岁的学生。
σSage < 20(Student)Sno
Sname
Ssex
Sage
Sdept
201215122
刘晨
女
19
IS
201215123
王敏
女
18
MA
201215125
张立
男
19
IS
🌕**2. 投影 **π
从R中选择出若干属性列组成新的关系 ** πA(R) = { t[A] | t ∈R } **,A:R中的属性列
示例:
查询学生的姓名和所在系。
即求Student关系上学生姓名和所在系两个属性上的投影
πSname,Sdept(Student)Sname
Sdept
李勇
CS
刘晨
CS
王敏
MA
张立
IS
查询学生关系Student中都有哪些系。
πSdept(Student)Sdept
CS
IS
MA
🌕3. 连接
从两个关系的笛卡尔积中选取属性间满足一定条件的元组
A和B:分别为R和S上度数相等且可比的属性组;θ:比较运算符
1. 连接分成 等值连接+自然连接
等值连接
θ为“=”的连接运算称为等值连接
自然连接
两个关系中进行比较的分量必须是相同的属性组+在结果中把重复的属性列去掉
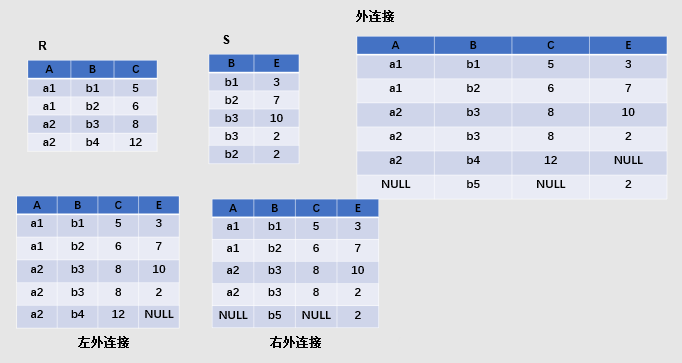
2. 外连接与左外连接和右外连接
悬浮元组:两个关系R和S在做自然连接时,关系R中某些元组有可能在S中不存在公共属性上值相等的元组,从而造成R中这些元组在操作时被舍弃了
两个关系中相同的属性组联合3.3 外连接:把悬浮元组也保存在结果关系中,而在其他属性上填空值(Null)
3.4 左外连接:只保留左边关系R中的悬浮元组
3.5 右外连接:只保留右边关系S中的悬浮元组
🌕**4. 除运算 **÷
给定关系R (X,Y) 和S (Y,Z),其中X,Y,Z为属性组。
R中的Y与S中的Y可以有不同的属性名,但必须出自相同的域集。
R与S的除运算得到一个新的关系P(X),
P是R中满足下列条件的元组在 X 属性列上的投影:
元组在X上分量值x的象集Yx包含S在Y上投影的集合,记作:
R÷S={tr[X] | tr∈R∧πY(S)∈Yx}
Yx:x在R中的象集,x = tr[X]示例
解释:
在关系R中,A可以取四个值{a1,a2,a3,a4}
- a1的象集为 {(b1,c2),(b2,c3),(b2,c1)}
- a2的象集为 {(b3,c7),(b2,c3)}
- a3的象集为 {(b4,c6)}
- a4的象集为 {(b6,c6)}
S在(B,C)上的投影为 {(b1,c2),(b2,c1),(b2,c3) }
只有a1的象集包含了S在(B,C)属性组上的投影
所以 R÷S ={a1}
📝总结
数据库SQL Server领域就像一片未被勘探的信息大海,引领你勇敢踏入数据科学的神秘领域。这是一场独特的学习冒险,从基本概念到算法实现,逐步揭示更深层次的模式分析、匹配算法和智能模式识别的奥秘。渴望挑战数据库SQL Server中的模式匹配学习路径和掌握信息领域的技术?不妨点击下方链接,一同探讨更多数据科学的奇迹吧。我们推出了引领趋势的💻 数据科学专栏:《数据之谜 | 数据奇迹解码》,旨在深度探索数据库SQL Server中模式匹配技术的实际应用和创新。🌐🔍


版权归原作者 SarPro 所有, 如有侵权,请联系我们删除。