xLSTM的新闻大家可能前几天都已经看过了,原作者提出更强的xLSTM,可以将LSTM扩展到数十亿参数规模,我们今天就来将其与原始的lstm进行一个详细的对比,然后再使用Pytorch实现一个简单的xLSTM。
xLSTM
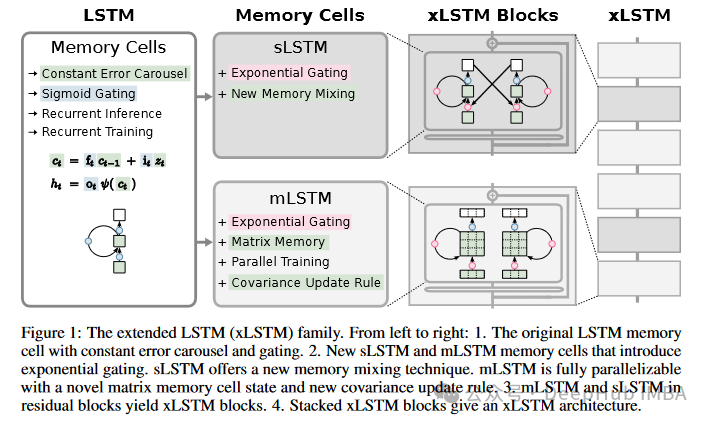
xLSTM 是对传统 LSTM 的一种扩展,它通过引入新的门控机制和记忆结构来改进 LSTM,旨在提高 LSTM 在处理大规模数据时的表现和扩展性。以下是 xLSTM 相对于原始 LSTM 的几个主要区别:
- 指数门控:- xLSTM 引入了指数门控机制,这是一种新的门控技术,与传统的 sigmoid 门控不同。指数门控可以提供更动态的信息过滤能力,有助于改善记忆和遗忘过程。
- 记忆结构的修改:- sLSTM:单一记忆体系结构中加入了新的记忆混合技术。它仍然保持标量更新,但通过改进的混合方式提高了信息的存储和利用效率。- mLSTM:引入矩阵记忆,这允许并行处理并改善了存储容量。它使用了协方差更新规则,适合处理大规模并行数据,解决了 LSTM 在并行化方面的限制。
- 归一化和稳定化技术:- 为了防止指数门控引起的数值稳定性问题,xLSTM 在门控计算中引入了额外的归一化和稳定化步骤,例如使用最大值记录法来维持稳定。
- 残差块的集成:- xLSTM 将这些改进的 LSTM 单元集成到残差块中,这些残差块被进一步堆叠形成完整的网络架构。这种设计使得 xLSTM 能够更有效地处理复杂的序列数据。
- 性能和扩展性:- xLSTM 在性能上与最新的 Transformer 和状态空间模型相媲美,尤其是在大规模应用和长序列处理方面展现出优势。
总的来说,xLSTM 的设计目标是解决传统 LSTM 在处理大规模数据和长序列时面临的限制,如并行性差和存储容量有限,通过引入新的门控机制和记忆结构,使其在现代深度学习应用中更具竞争力。
LSTM基础
要讲解xLSTM我们先简单回顾一下LSTM,论文中也给出了LSTM的公式,我们直接引用。
传统的 LSTM (长短期记忆网络) 的计算公式涉及几个关键部分:输入门(iti_tit)、遗忘门(ftf_tft)、输出门(oto_tot)和单元状态(ctc_tct)。以下是 LSTM 单元的标准计算步骤:
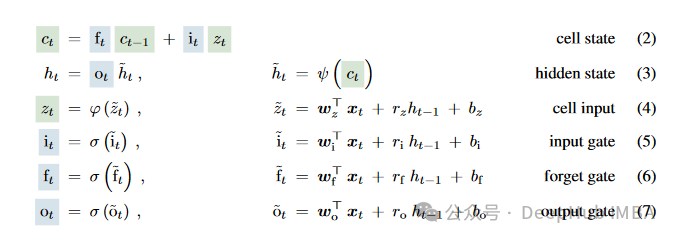
xLSTM改进
xLSTM之所以称之为xLSTM就是因为它将LSTM扩展为多个LSTM的变体,sLSTM和mLSTM,每种变体都针对特定的性能和功能进行优化,以处理各种复杂的序列数据问题。
sLSTM
sLSTM(Scalar LSTM)在传统的LSTM基础上增加了标量更新机制。这种设计通过对内部记忆单元进行细粒度的控制,优化了门控机制,使其更适合处理有着细微时间变化的序列数据。sLSTM通常会使用指数门控和归一化技术,以改善模型在长序列数据处理上的稳定性和准确性。通过这种方式,sLSTM能够在保持较低计算复杂度的同时,提供与复杂模型相当的性能,特别适用于资源受限的环境或需要快速响应的应用。
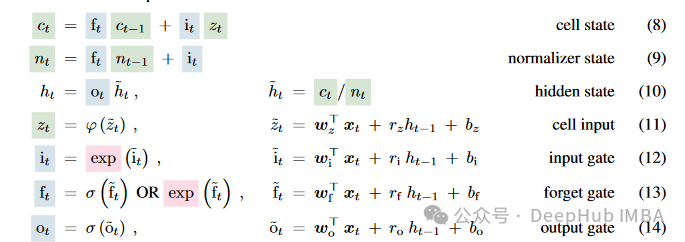
可以说上面的只是对传统的LSTM进行了一些简单的修改,基本上的计算流程还都是一样的。
mLSTM
mLSTM(Matrix LSTM)通过将传统的LSTM中的向量操作扩展到矩阵操作,极大地增强了模型的记忆能力和并行处理能力。mLSTM的每个状态不再是单一的向量,而是一个矩阵,这使得它可以在单个时间步内捕获更复杂的数据关系和模式。mLSTM特别适合于处理大规模数据集或需要高度复杂数据模式识别的任务。此外,mLSTM的设计支持高度并行化处理,这不仅提高了计算效率,还允许模型更好地扩展到大规模数据集上。

mLSTM可以说是最新的版本了,但是如果你仔细看代码,是不是有几个很熟悉的单词呢?K,Q,V,这不是出现在transformer中的注意力机制的表示吗?对,其实就是这样的,只不过计算的方式不同。
所以这样才能使得LSTM变得并行化,这个后面我们细说
残差网络块
xLSTM中的残差网络块是其架构中的一个重要组成部分,这些块的设计使得xLSTM能够有效地处理复杂的序列数据,同时提高模型在深层网络中的训练稳定性。残差网络块通过引入跳过连接来缓解深层神经网络训练过程中的梯度消失问题。这应该是让xLSTM可以堆叠多层的一个原因。因为如果你以前使用过LSTM的话,你肯定知道,LSTM一般都是2层就可以了,因为再多也不会产生效果,而且计算速度很慢。
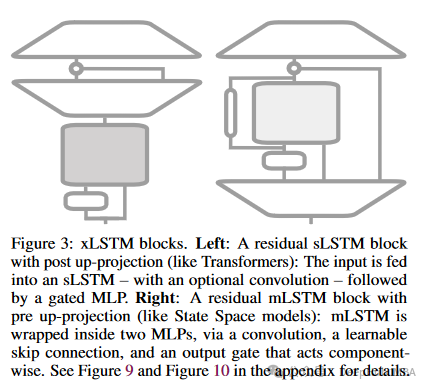
xLSTM的残差网络块由以下几部分构成:
- 主路径:- 主路径包含核心的xLSTM计算单元,这可能是sLSTM或mLSTM单元,负责进行复杂的序列处理和记忆操作。- 这些单元接受来自前一块的输入,执行必要的门控和状态更新操作,然后输出到后续的处理步骤。
- 跳过连接(Skip Connection):- 跳过连接直接将输入传递到块的输出,与主路径输出相加。- 这样的设计有助于网络在深层传递时保持信息不丢失,同时减轻梯度消失的问题。
- 标准化层(如层归一化或批归一化):- 在残差块的输入或输出端通常会加入标准化层,以稳定训练过程中的数据分布,提高模型的训练效率和泛化能力。
- 非线性激活函数:- 在将主路径输出与跳过连接的输出相加后,通常会通过一个非线性激活函数,如ReLU或tanh,以引入必要的非线性处理能力,增强模型的表达能力。
以上就是xLSTM论文的一些解释,下面我们直接上代码
Pytorch的实现
我们为了说明问题,简单实现一个xLSTM
importtorch
importtorch.nnasnn
importtorch.nn.functionalasF
classCausalConv1D(nn.Module):
def__init__(self, in_channels, out_channels, kernel_size, dilation=1, **kwargs):
super(CausalConv1D, self).__init__()
self.padding= (kernel_size-1) *dilation
self.conv=nn.Conv1d(in_channels, out_channels, kernel_size, padding=self.padding, dilation=dilation, **kwargs)
defforward(self, x):
x=self.conv(x)
returnx[:, :, :-self.padding]
classBlockDiagonal(nn.Module):
def__init__(self, in_features, out_features, num_blocks):
super(BlockDiagonal, self).__init__()
self.in_features=in_features
self.out_features=out_features
self.num_blocks=num_blocks
assertin_features%num_blocks==0
assertout_features%num_blocks==0
block_in_features=in_features//num_blocks
block_out_features=out_features//num_blocks
self.blocks=nn.ModuleList([
nn.Linear(block_in_features, block_out_features)
for_inrange(num_blocks)
])
defforward(self, x):
x=x.chunk(self.num_blocks, dim=-1)
x= [block(x_i) forblock, x_iinzip(self.blocks, x)]
x=torch.cat(x, dim=-1)
returnx
classsLSTMBlock(nn.Module):
def__init__(self, input_size, hidden_size, num_heads, proj_factor=4/3):
super(sLSTMBlock, self).__init__()
self.input_size=input_size
self.hidden_size=hidden_size
self.num_heads=num_heads
self.head_size=hidden_size//num_heads
self.proj_factor=proj_factor
asserthidden_size%num_heads==0
assertproj_factor>0
self.layer_norm=nn.LayerNorm(input_size)
self.causal_conv=CausalConv1D(1, 1, 4)
self.Wz=BlockDiagonal(input_size, hidden_size, num_heads)
self.Wi=BlockDiagonal(input_size, hidden_size, num_heads)
self.Wf=BlockDiagonal(input_size, hidden_size, num_heads)
self.Wo=BlockDiagonal(input_size, hidden_size, num_heads)
self.Rz=BlockDiagonal(hidden_size, hidden_size, num_heads)
self.Ri=BlockDiagonal(hidden_size, hidden_size, num_heads)
self.Rf=BlockDiagonal(hidden_size, hidden_size, num_heads)
self.Ro=BlockDiagonal(hidden_size, hidden_size, num_heads)
self.group_norm=nn.GroupNorm(num_heads, hidden_size)
self.up_proj_left=nn.Linear(hidden_size, int(hidden_size*proj_factor))
self.up_proj_right=nn.Linear(hidden_size, int(hidden_size*proj_factor))
self.down_proj=nn.Linear(int(hidden_size*proj_factor), input_size)
defforward(self, x, prev_state):
assertx.size(-1) ==self.input_size
h_prev, c_prev, n_prev, m_prev=prev_state
x_norm=self.layer_norm(x)
x_conv=F.silu(self.causal_conv(x_norm.unsqueeze(1)).squeeze(1))
z=torch.tanh(self.Wz(x) +self.Rz(h_prev))
o=torch.sigmoid(self.Wo(x) +self.Ro(h_prev))
i_tilde=self.Wi(x_conv) +self.Ri(h_prev)
f_tilde=self.Wf(x_conv) +self.Rf(h_prev)
m_t=torch.max(f_tilde+m_prev, i_tilde)
i=torch.exp(i_tilde-m_t)
f=torch.exp(f_tilde+m_prev-m_t)
c_t=f*c_prev+i*z
n_t=f*n_prev+i
h_t=o*c_t/n_t
output=h_t
output_norm=self.group_norm(output)
output_left=self.up_proj_left(output_norm)
output_right=self.up_proj_right(output_norm)
output_gated=F.gelu(output_right)
output=output_left*output_gated
output=self.down_proj(output)
final_output=output+x
returnfinal_output, (h_t, c_t, n_t, m_t)
classsLSTM(nn.Module):
# TODO: Add bias, dropout, bidirectional
def__init__(self, input_size, hidden_size, num_heads, num_layers=1, batch_first=False, proj_factor=4/3):
super(sLSTM, self).__init__()
self.input_size=input_size
self.hidden_size=hidden_size
self.num_heads=num_heads
self.num_layers=num_layers
self.batch_first=batch_first
self.proj_factor_slstm=proj_factor
self.layers=nn.ModuleList([sLSTMBlock(input_size, hidden_size, num_heads, proj_factor) for_inrange(num_layers)])
defforward(self, x, state=None):
assertx.ndim==3
ifself.batch_first: x=x.transpose(0, 1)
seq_len, batch_size, _=x.size()
ifstateisnotNone:
state=torch.stack(list(state))
assertstate.ndim==4
num_hidden, state_num_layers, state_batch_size, state_input_size=state.size()
assertnum_hidden==4
assertstate_num_layers==self.num_layers
assertstate_batch_size==batch_size
assertstate_input_size==self.input_size
state=state.transpose(0, 1)
else:
state=torch.zeros(self.num_layers, 4, batch_size, self.hidden_size)
output= []
fortinrange(seq_len):
x_t=x[t]
forlayerinrange(self.num_layers):
x_t, state_tuple=self.layers[layer](x_t, tuple(state[layer].clone()))
state[layer] =torch.stack(list(state_tuple))
output.append(x_t)
output=torch.stack(output)
ifself.batch_first:
output=output.transpose(0, 1)
state=tuple(state.transpose(0, 1))
returnoutput, state
classmLSTMBlock(nn.Module):
def__init__(self, input_size, hidden_size, num_heads, proj_factor=2):
super(mLSTMBlock, self).__init__()
self.input_size=input_size
self.hidden_size=hidden_size
self.num_heads=num_heads
self.head_size=hidden_size//num_heads
self.proj_factor=proj_factor
asserthidden_size%num_heads==0
assertproj_factor>0
self.layer_norm=nn.LayerNorm(input_size)
self.up_proj_left=nn.Linear(input_size, int(input_size*proj_factor))
self.up_proj_right=nn.Linear(input_size, hidden_size)
self.down_proj=nn.Linear(hidden_size, input_size)
self.causal_conv=CausalConv1D(1, 1, 4)
self.skip_connection=nn.Linear(int(input_size*proj_factor), hidden_size)
self.Wq=BlockDiagonal(int(input_size*proj_factor), hidden_size, num_heads)
self.Wk=BlockDiagonal(int(input_size*proj_factor), hidden_size, num_heads)
self.Wv=BlockDiagonal(int(input_size*proj_factor), hidden_size, num_heads)
self.Wi=nn.Linear(int(input_size*proj_factor), hidden_size)
self.Wf=nn.Linear(int(input_size*proj_factor), hidden_size)
self.Wo=nn.Linear(int(input_size*proj_factor), hidden_size)
self.group_norm=nn.GroupNorm(num_heads, hidden_size)
defforward(self, x, prev_state):
h_prev, c_prev, n_prev, m_prev=prev_state
assertx.size(-1) ==self.input_size
x_norm=self.layer_norm(x)
x_up_left=self.up_proj_left(x_norm)
x_up_right=self.up_proj_right(x_norm)
x_conv=F.silu(self.causal_conv(x_up_left.unsqueeze(1)).squeeze(1))
x_skip=self.skip_connection(x_conv)
q=self.Wq(x_conv)
k=self.Wk(x_conv) / (self.head_size**0.5)
v=self.Wv(x_up_left)
i_tilde=self.Wi(x_conv)
f_tilde=self.Wf(x_conv)
o=torch.sigmoid(self.Wo(x_up_left))
m_t=torch.max(f_tilde+m_prev, i_tilde)
i=torch.exp(i_tilde-m_t)
f=torch.exp(f_tilde+m_prev-m_t)
c_t=f*c_prev+i* (v*k) # v @ k.T
n_t=f*n_prev+i*k
h_t=o* (c_t*q) /torch.max(torch.abs(n_t.T@q), 1)[0] # o * (c @ q) / max{|n.T @ q|, 1}
output=h_t
output_norm=self.group_norm(output)
output=output_norm+x_skip
output=output*F.silu(x_up_right)
output=self.down_proj(output)
final_output=output+x
returnfinal_output, (h_t, c_t, n_t, m_t)
classmLSTM(nn.Module):
# TODO: Add bias, dropout, bidirectional
def__init__(self, input_size, hidden_size, num_heads, num_layers=1, batch_first=False, proj_factor=2):
super(mLSTM, self).__init__()
self.input_size=input_size
self.hidden_size=hidden_size
self.num_heads=num_heads
self.num_layers=num_layers
self.batch_first=batch_first
self.proj_factor_slstm=proj_factor
self.layers=nn.ModuleList([mLSTMBlock(input_size, hidden_size, num_heads, proj_factor) for_inrange(num_layers)])
defforward(self, x, state=None):
assertx.ndim==3
ifself.batch_first: x=x.transpose(0, 1)
seq_len, batch_size, _=x.size()
ifstateisnotNone:
state=torch.stack(list(state))
assertstate.ndim==4
num_hidden, state_num_layers, state_batch_size, state_input_size=state.size()
assertnum_hidden==4
assertstate_num_layers==self.num_layers
assertstate_batch_size==batch_size
assertstate_input_size==self.input_size
state=state.transpose(0, 1)
else:
state=torch.zeros(self.num_layers, 4, batch_size, self.hidden_size)
output= []
fortinrange(seq_len):
x_t=x[t]
forlayerinrange(self.num_layers):
x_t, state_tuple=self.layers[layer](x_t, tuple(state[layer].clone()))
state[layer] =torch.stack(list(state_tuple))
output.append(x_t)
output=torch.stack(output)
ifself.batch_first:
output=output.transpose(0, 1)
state=tuple(state.transpose(0, 1))
returnoutput, state
classxLSTM(nn.Module):
# TODO: Add bias, dropout, bidirectional
def__init__(self, input_size, hidden_size, num_heads, layers, batch_first=False, proj_factor_slstm=4/3, proj_factor_mlstm=2):
super(xLSTM, self).__init__()
self.input_size=input_size
self.hidden_size=hidden_size
self.num_heads=num_heads
self.layers=layers
self.num_layers=len(layers)
self.batch_first=batch_first
self.proj_factor_slstm=proj_factor_slstm
self.proj_factor_mlstm=proj_factor_mlstm
self.layers=nn.ModuleList()
forlayer_typeinlayers:
iflayer_type=='s':
layer=sLSTMBlock(input_size, hidden_size, num_heads, proj_factor_slstm)
eliflayer_type=='m':
layer=mLSTMBlock(input_size, hidden_size, num_heads, proj_factor_mlstm)
else:
raiseValueError(f"Invalid layer type: {layer_type}. Choose 's' for sLSTM or 'm' for mLSTM.")
self.layers.append(layer)
defforward(self, x, state=None):
assertx.ndim==3
ifself.batch_first: x=x.transpose(0, 1)
seq_len, batch_size, _=x.size()
ifstateisnotNone:
state=torch.stack(list(state))
assertstate.ndim==4
num_hidden, state_num_layers, state_batch_size, state_input_size=state.size()
assertnum_hidden==4
assertstate_num_layers==self.num_layers
assertstate_batch_size==batch_size
assertstate_input_size==self.input_size
state=state.transpose(0, 1)
else:
state=torch.zeros(self.num_layers, 4, batch_size, self.hidden_size)
output= []
fortinrange(seq_len):
x_t=x[t]
forlayerinrange(self.num_layers):
x_t, state_tuple=self.layers[layer](x_t, tuple(state[layer].clone()))
state[layer] =torch.stack(list(state_tuple))
output.append(x_t)
output=torch.stack(output)
ifself.batch_first:
output=output.transpose(0, 1)
state=tuple(state.transpose(0, 1))
returnoutput, state
CausalConv1D
是一个因果卷积层,用于保证在处理时序数据时不违反时间的因果关系。这个类的实现确保卷积操作不会看到未来的信息,这对于序列预测任务非常重要。
BlockDiagonal
实现了一个特殊的线性(全连接)层,其权重矩阵由多个独立的块(block)组成,这些块在主对角线上排列,形成了一个块对角矩阵。这种设计允许层在处理输入时,每个块只与输入的对应部分进行交互,从而模拟了多个独立的线性变换的集合。
对于
BlockDiagonal
我们还看到他还有一个参数
num_blocks
就是复制多少个内部的线性层,对于transformer里面就是多头注意力的注意力头数。
sLSTMBlock
在论文中,sLSTM 通常描述为带有标量或序列级更新的 LSTM 增强版,可能包括对门控机制的改进(如指数门控)以及内存结构的优化。论文中可能更侧重于通过算法优化来增强 LSTM 的功能,而不是像代码实现中那样使用复杂的网络层和结构。
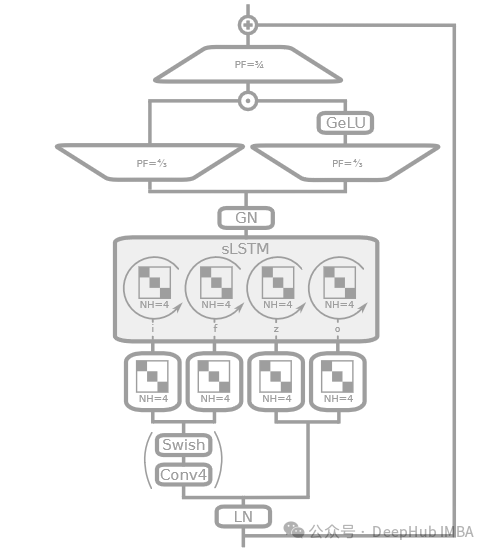
- 代码中使用了层归一化(LayerNorm)来稳定每层的输入。
- 引入了因果卷积(CausalConv1D),这在处理序列数据时可以保证信息的时间顺序性,避免未来信息的泄露。
- 使用了分块对角线矩阵变换(BlockDiagonal)来并行处理不同头的数据。
- 实现了残差连接,增加了模型处理深层网络时的稳定性。
- 使用了 GELU 和 GroupNorm 对输出进行非线性变换和归一化处理。
mLSTMBlock
mLSTM 在论文中描述为具有矩阵记忆的 LSTM 变体,可以并行处理和存储更多的信息。这通常涉及到记忆结构的本质改变,如使用矩阵而非标量来存储 LSTM 的单元状态。
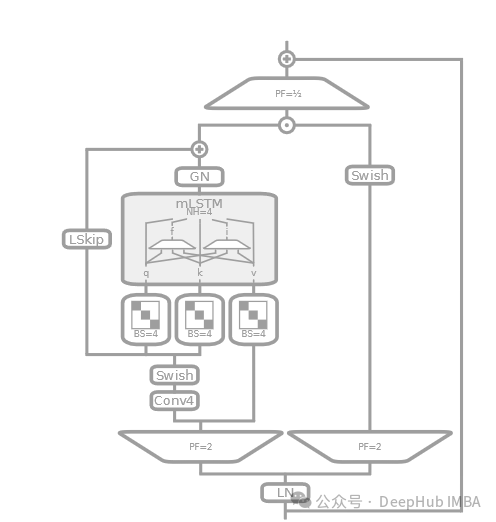
- 类似于 sLSTMBlock,使用了层归一化和因果卷积,以及残差连接。
- 采用了独特的投影策略,如投影到更高维空间再通过激活函数和线性变换处理。
- 强调了矩阵记忆的使用,这在 mLSTM 中表现为对输入和隐藏状态的矩阵操作,以及使用 BlockDiagonal 进行分块处理。
对于mLSTMBlock.并行的矩阵操作
查询、键和值的计算本质上是矩阵乘法操作,这是并行计算中最常优化的操作之一。
q=self.Wq(x_conv)
k=self.Wk(x_conv) / (self.head_size**0.5)
v=self.Wv(x_up_left)
---
c_t=f*c_prev+i* (v*k) # v @ k.T
n_t=f*n_prev+i*k
h_t=o* (c_t*q) /torch.max(torch.abs(n_t.T@q), 1)[0] # o * (c @ q) / max{|n.T @ q|, 1}
在mLSTM 中,使用矩阵而不是标量来更新和存储隐藏状态,所以论文中提到与transformer相反,xLSTM网络具有线性计算和相对于序列长度的恒定内存复杂度
但是论文的原话是 The memory of mLSTM does not require parameters but is computationally expensive through its d×d matrix memory and d × d update. We trade off memory capacity against computational complexity.
这就是我在前面说的是不是很像transformer的注意力,或者说mLSTM也记录了以前所有序列的一个隐藏状态,然后当前的状态是和序列前面的所有状态有关的。
sLSTM还是mLSTM
论文中也没有具体说明 sLSTM 和 mLSTM 是如何结合使用的,所以我们的代码中也没有具体的堆叠规则,也就是说可能需要我们自己去判断了,但是可以看到应该是尽量少用sLSTM 把,因为他没法并行,并且论文中也说到sLSTM 无法并行,并且慢两倍。
sLSTM is not parallelizable due to the memory mixing (hidden-hidden connections).However, we developed a fast CUDA implementation with GPU memory optimizations to the registerlevel which is typically less than two times slower than mLSTM.
总结
最后我们做个小结,sLSTM可以说是以前LSTM的更新版,并且也无法并行化,所以计算会很慢。
而新的mLSTM则是一种新的架构,使用 d×d 矩阵来存储隐藏状态,所以mLSTM 面临着高计算复杂度。尽管 mLSTM 中的内存更新和检索过程不使用参数,并且可以使用标准矩阵操作并行化,但由于矩阵内存的复杂性,仍有一些小的墙钟时间开销。
论文还提到的一点是尽管mLSTM 的矩阵内存与序列长度无关,但在处理更长的上下文大小时可能会变得过载。论文指出这对于多达 16,000 个标记的上下文似乎不是一个限制。
但是无论怎样xLSTM作为一种扩展的LSTM模型,提出了包括sLSTM和mLSTM在内的不同变体,以增强其处理各种复杂序列数据的能力。sLSTM优化了门控机制,适用于处理具有细微时间变化的序列,而mLSTM通过使用矩阵代替传统的向量来增强模型的记忆和并行处理能力,特别适合于大规模数据处理。
所以我们现在已经有4个主要的基础模块了 xLSTM,Mamba,RWKV,Transformer。有时间我会把这几个模块做一个详细的对比。
最后因为官方还没有给出代码,所以目前网上看到的都是大佬们的非官方实现,并且有人做了相关的索引,有兴趣的可以直接查看: