数据结构与算法 之线性表

**⭐️大一小何，还在学习当中，欢迎交流指正~ **

嘿嘿~[doge]

线性表

线性表(Linear List)
是由有限个相同类型的数据元素组成的有序序列，一般记作(a,,a2,…….an)

特点:
除了a1和an之外，任意元素ai都有一个直接前趋ai-1和一个直接后继ai+1;

a1无前趋
an无后继

线性表的基本操作

采用顺序存储结构的称为顺序表 采用链式存储结构的称为线性链表

顺序表

顺序表的特点:以物理位置相邻表示逻辑关系

顺序表的优点:任一元素均可随机存取。

顺序表的缺点:进行插入和删除操作时，需移动大量的元素。
存储空间不灵活

Status Listlnsert_Sq(SqList &L,int i,ElemType e){
    if(i<1 || i>L.length+1) return ERROR;//i值不合法
    if(L.length==MAXSIZE)return ERROR;//当前存储空间已满
    for(j=L.length-1;j>=i-1;j--)
        L.elem[j+1]=L.elem[j];//插入位置及之后的元素后移
    
        L.elem[i-1]=e;//将新元素e放入第i个位置
    
     L.length++;//表长增1
    
    return OK;
}

空表

如何表示空表?

1.无头结点时，头指针为空时表示空表；

2.有头结点时，当头结点的指针域为空时表示空表

下面用几个图形象的表示一下空表和非空表

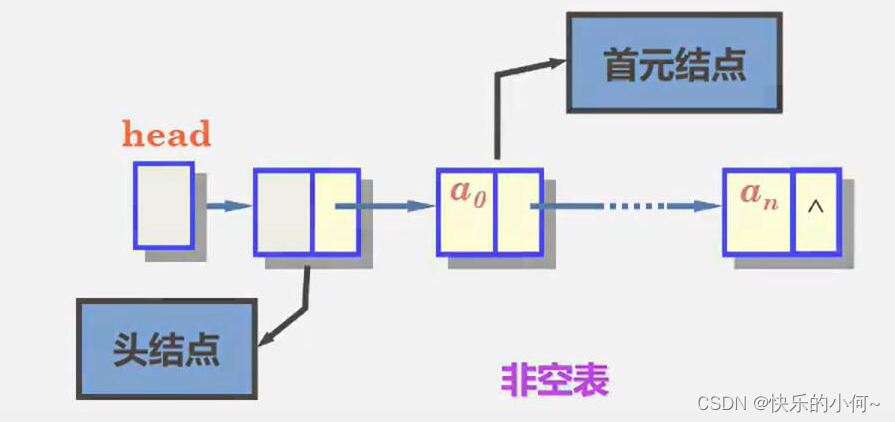
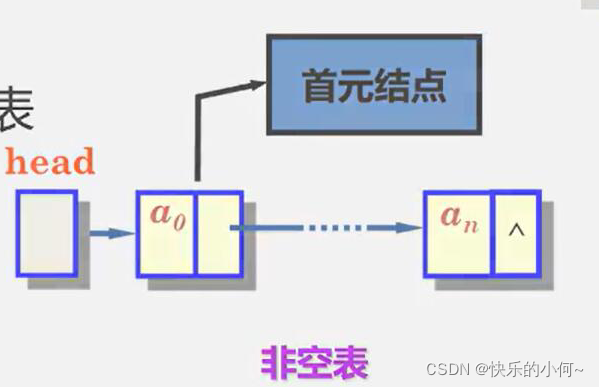
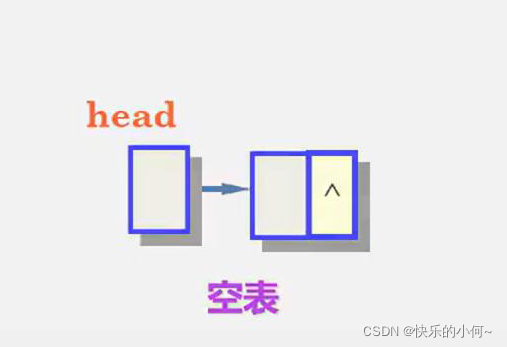
单链表

单链表:每个结点只有一个指针域

双链表

双链表:每个结点有两个指针域

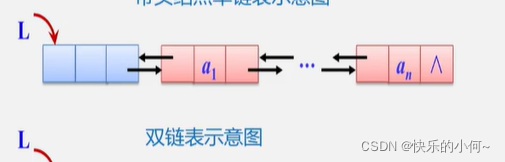
循环链表

循环链表:链表结点首尾相接

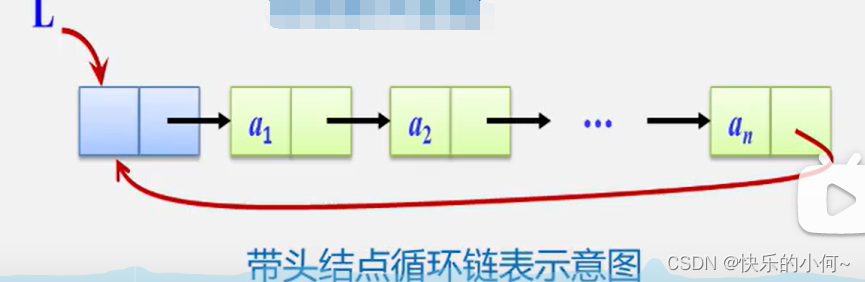
销毁单链表

链表销毁后不存在

从头指针开始，依次释放所有结点

像这样

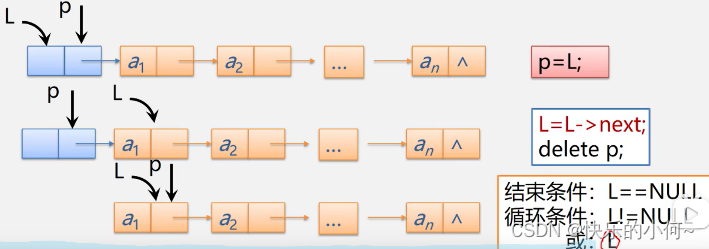
销毁单链表L

Status DestroyList_L(LinkList &L){//销毁单链表L
    Lnode *p;//或LinkList p;
    while(L){
        p=L;
    L=L->next;
    delete p;
}

清空单链表

链表仍存在，但链表中无元素，成为空链表（头指针和头结点仍然在）；

依次释放所有结点，并将头结点指针域设置为空

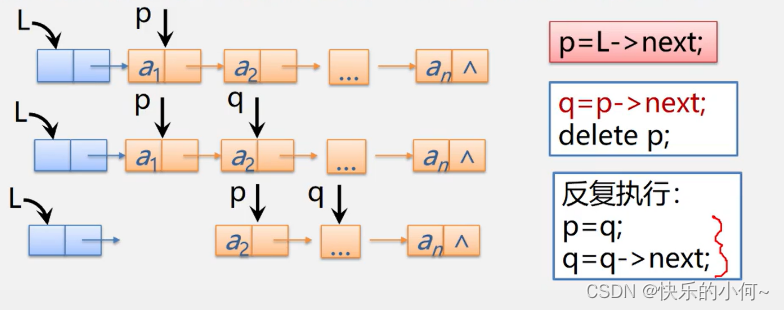
清空链表L:
Status ClearList(LinkList & L){//将L重置为空表

    Lnode *p,*q;//或LinkList p,q;
    p=L->next;
    while(p){//没到表尾

    q=p->next;
    delete p;
    p=q;
}
    L->next=NULL;//头结点指针域为空

    return OK;
}

求单链表的表长

int ListLength_L(LinkList L){
    LinkList p;
    p=L->next;
    i=0;
    while(p){
        i++；
        p=p->next;
    }
    return i;
}

取第i个元素值

Status GetElem_L(LinkList L,int i,ElemType &e){
    p=L->next;  //初始化
    j=1;        //初始化
    while(p&&j<i){  //向后扫描，直到p指向第i个元素或p为空
        p=p->next;
        j++;
    }
    if(!p\\j>i) return ERROR;   //第i个元素不存在
    e=p->data;                  //取第i个元素
    return OK;
}//GetElem_L

按值查找

1.从第一个结点起，依次和e相比较。
2.如果找到一个其值与e相等的数据元素，则返回其在链表中的位置”)或地址;
3.如果查遍整个链表都没有找到其值和e相等的元素，则返回0或
"NULL”

算法描述】
Lnode *LocateELem_L (LinkList L, Elemtype e){
//在线性表L中查找值为e的数据元素
//找到，则返回L中值为e的数据元素的地址，查找失败返回NULL
    p=L->next;
    while(p &&p->data!=e)
        p=p->next;
    return p;
}

按值查找 根据指定数据获取该数据位置序号

//在线性表L中查找值为e的数据元素的位置序号
int LocateELem_L (LinkList L,Elemtype e) {
//返回L中值为e的数据元素的位置序号，查找失败返回0
    p=L->next; 
    j=1;
    while(p &&p->data!=e)
    {
        p=p->next;
         j++;
    }
    if(p) 
        return j;
    else 
        return 0;
}

插入节点

不可以先执行2，后执行1，否则会丢失ai的地址

//在L中第i个元素之前插入数据元素e
Status Listlnsert_L(LinkList &L,int i,ElemType e){
    p=L; 
    j=o;
   while(p && j<i-1)
    { 
        p=p->next; 
        ++j; 
    }//寻找第i-1个结点，p指向i-1结点
    if(!p llj>i-1)
        return ERROR;//i大于表长+1或者小于1，插入位置非法
    s=new LNode;
     s->data=e;//生成新结点s，将结点s的数据域置为e
    s->next=p->next;
    //将结点s插入L中
    p->next=s;
    return OK;
    }//ListInsert_L

删除节点

//将线性表L中第i个数据元素删除
Status ListDelete_L(LinkList &L,int i,ElemType &e){
    p=L;
    j=O;
    while(p->next &&j<i-1)
    {     p=p->next;
        ++j; }//寻找第i个结点，并令p指向其前驱

    if(!(p->next)|lj>i-1) 
        return ERROR;//删除位置不合理
    q=p->next;//临时保存被删结点的地址以备释放

    p->next=q->next;//改变删除结点前驱结点的指针域
    
    e=q->data;//保存删除结点的数据域
    
    delete q;//释放删除结点的空间
  
    return OK;
}//ListDelete_L

查找插入删除分析

2.5.2单链表基本操作的实现
单链表的查找、插入、删除算法时间效率分析

1．查找:
因线性链表只能顺序存取，即在查找时要从头指针找起，查找的时间复杂度为O(n)。

2.插入和删除:
因线性链表不需要移动元素，只要修改指针，一般情况下时间复杂度为O(1)。

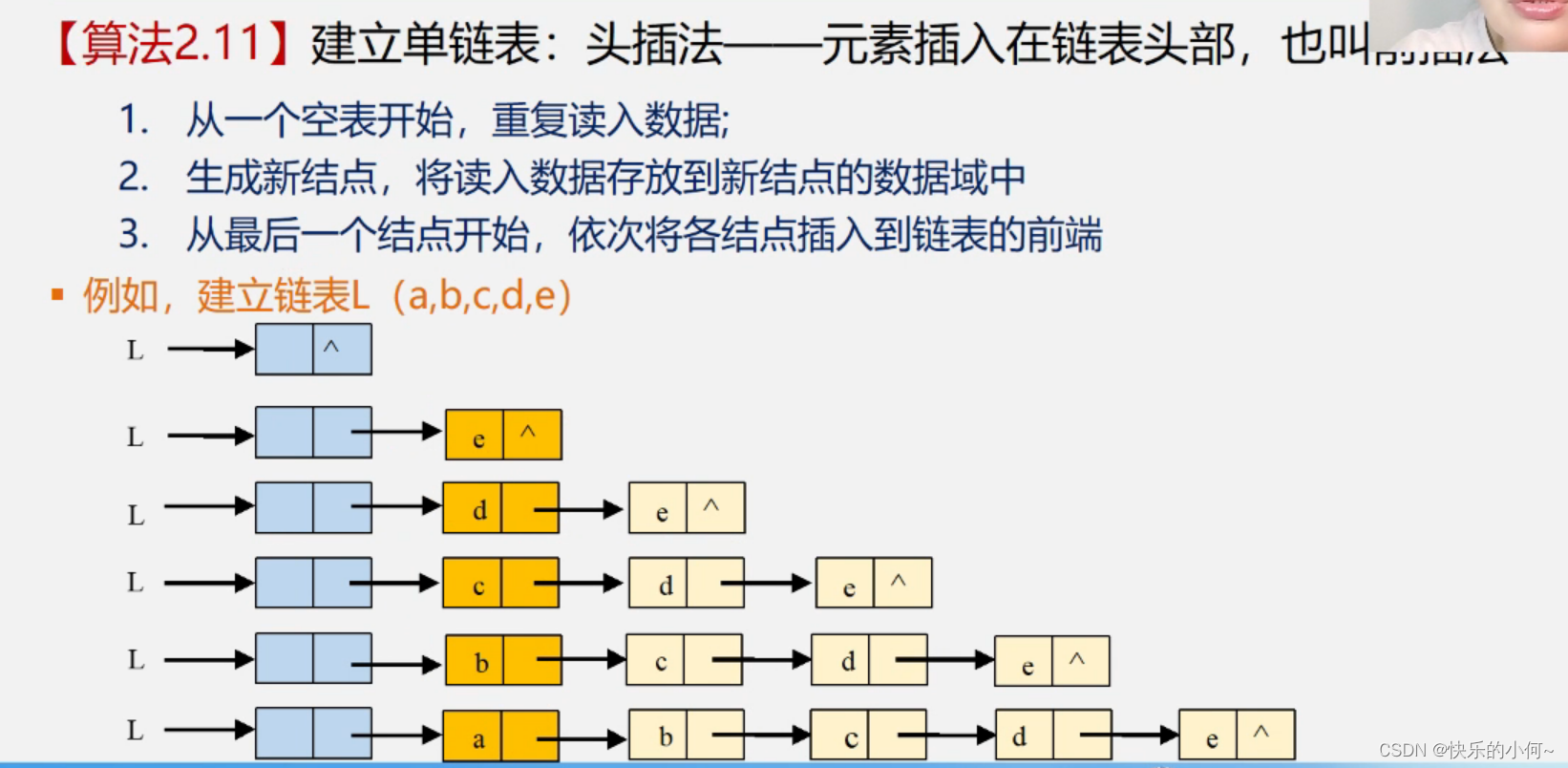
头插法建立链表

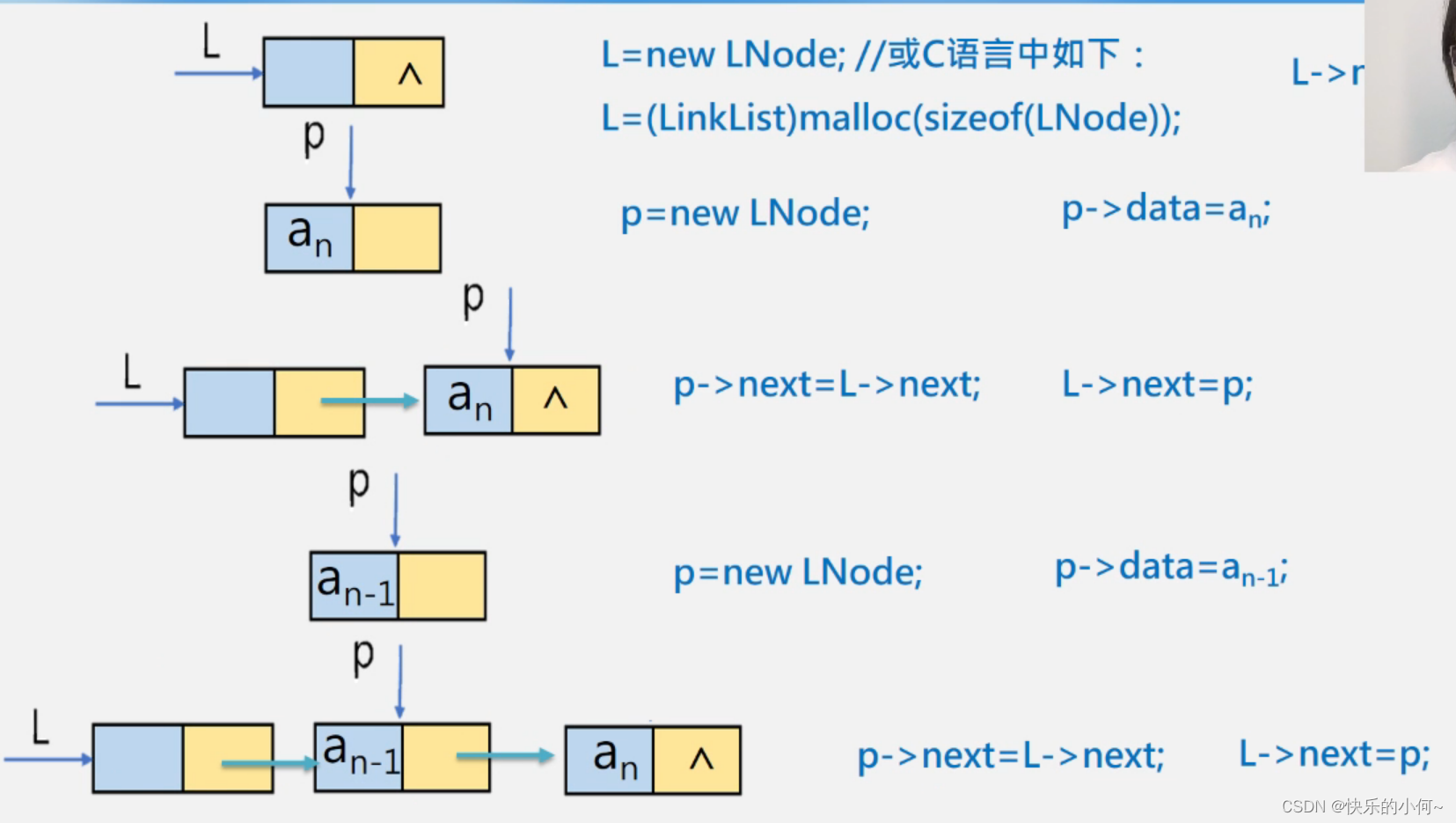
void CreateList_H(LinkList &L,int n){
    L=new LNode;
    L->next=NULL;//先建立一个带头结点的单链表
       for(i=n;i>O;--i){
            p=new LNode;//生成新结点p=(LNode*)malloc(sizeof(LNode));
            cin> >p->data;//辅入元素值scanf(&p-> data);
            p->next=L->next;//插入到表头

            L->next=p;
    }

}//CreateList H
//算法的时间复杂度是:0(n)

尾插法建立链表

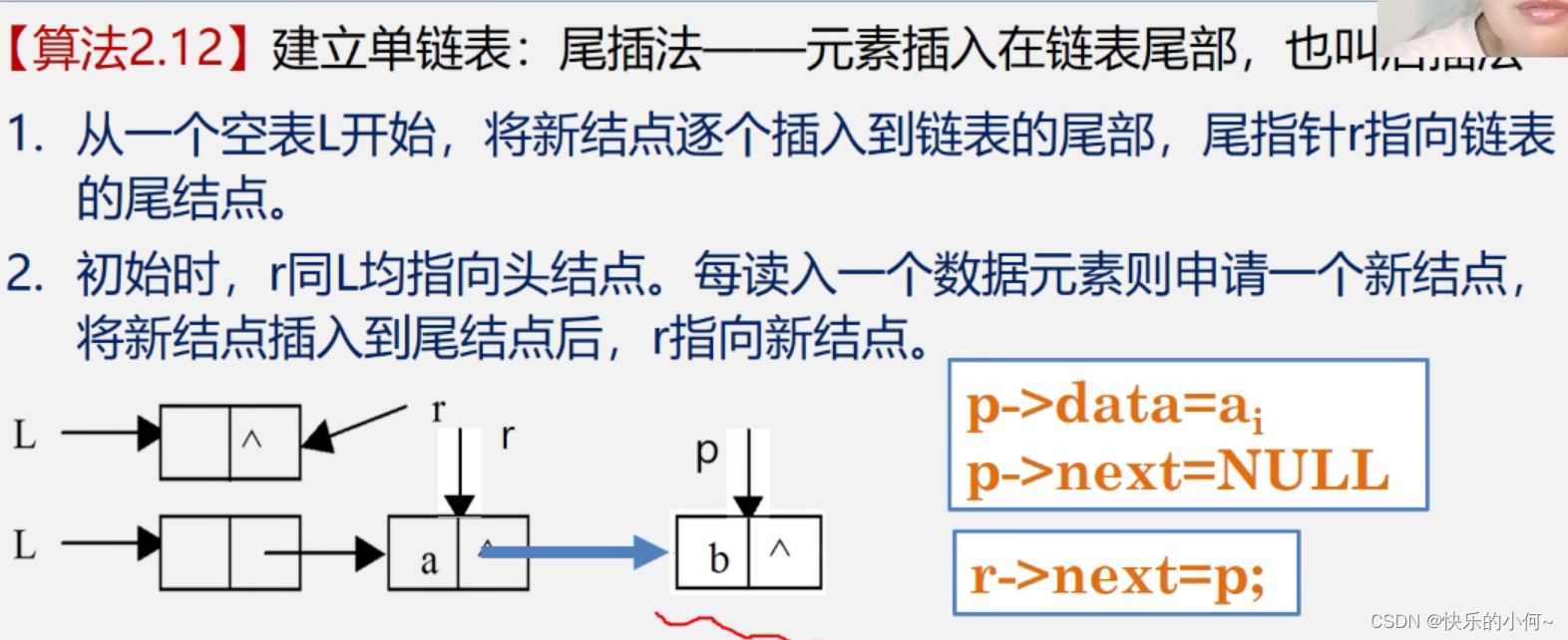
//正位序输入n个元素的值，建立带表头结点的单链表L
void CreateList_R(LinkList &L, int n){
    L=new LNode;
     L->next=NULL;
    r=L;//尾指针r指向头结点
    for(i=o;i<n;++i){
        p=new LNode;
         cin> >p->data;//生成新结点，输入元素值
        p->next=NULL;
        r->next=p;//插入到表尾

        r=p;//r指向新的尾结点
}

结语

一起加油哦~