基于Pytorch的强化学习(DQN)之策略学习

1. 引言

我们上次讲到了价值学习，这次我们来看看基于策略的学习，我们状态价值函数 $V_{\pi}(s_t)$ 能够描述当前状态下局势的好坏，如果 $V_{\pi}(s_t)$ 越大那局势不就会越好吗，所以我们得到了策略学习的基本思想：找到最优的action使 $V_{\pi}(s_t)$ 达到最大。

2. 数学推导

2.1 状态价值函数

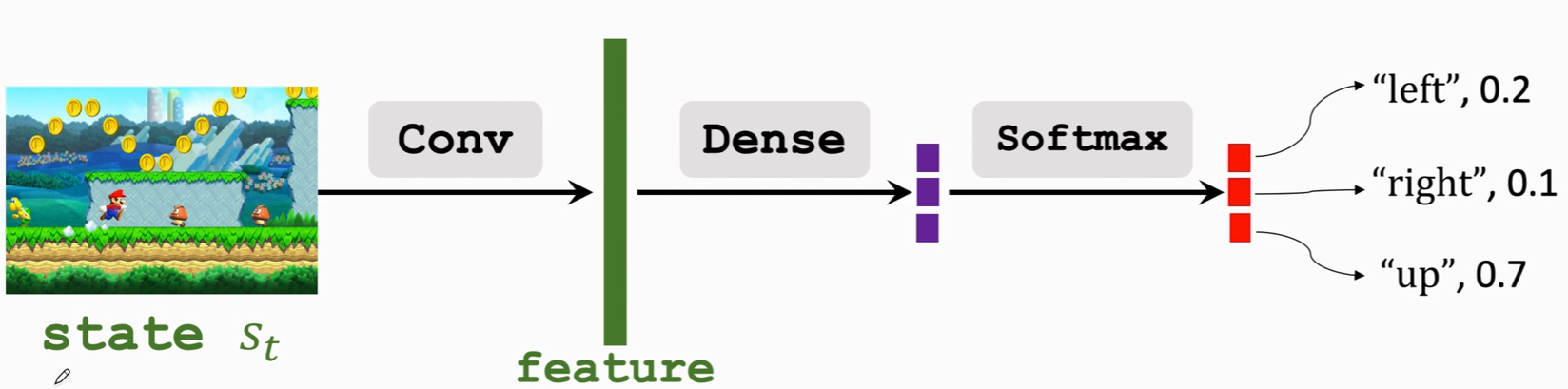
我们之前知道状态价值函数 $V_{\pi}(s_t)=E_A[Q_{\pi}(S_t,A)]=\sum_a{\pi}(a|s_t) Q_{\pi}(s_t,a)$ ，我们先用神经网络 $V_{\pi}(s_t,\theta)$ 来近似 $V_{\pi}$ ，这里的 $\theta$ 是神经网络的参数，如果我们认为 $Q_{\pi}$ 与 $\theta$ 无关，那么 $V_{\pi}(s_t,\theta)=\sum_a{\pi}(a|s_t,\theta) Q_{\pi}(s_t,a)$ 下面我们来求策略梯度。

2.2 策略梯度

我们将 $g(a,\theta)=\frac{\partial \,V_{\pi}(s,\theta)}{\partial \,\theta}$ 称为策略梯度，由于我们的目标是使 $V_{\pi}(s_t,\theta)$ 变大，所以我们使用梯度上升 $\theta\leftarrow\theta+\beta g(a,\theta)$ 来更新参数 $\theta$ ,我们经过如下的公式推导：

$g(a,\theta)=\frac{\partial \,V_{\pi}(s_t,\theta)}{\partial \,\theta}=\frac{\partial \,\sum_a{\pi}(a|s;\theta)Q_{\pi}(s,a)}{\partial \,\theta}=\sum_a{\pi}(a|s;\theta)\frac{\partial \,\ln{\pi}(a|s;\theta)}{\partial \,\theta}Q_{\pi}(s,a)=E_A[\frac{\partial \,\ln{\pi}(a|s;\theta)}{\partial \,\theta}Q_{\pi}(s,a)]$

第三个等式处的变形就是为了利用 ${\pi}(a|s;\theta)$ 使概率密度函数的性质将其写成期望的形式

上面是action为离散情况下的表达形式，那么如果是连续情况呢？这就需要使用蒙特卡罗近似了。

2.3 蒙特卡罗近似

蒙特卡洛近似本质上是一种基于统计原理的近似方法，我们抽取多次动作，次数越多近似就越准确，这样将连续问题离散化，我们就仍可以使用上面的公式了，例如我从action中随机抽取了一个 $a_0$ ,我们便有 $g(a_0,\theta)=\frac{\partial \,\ln{\pi}(a_0|s;\theta)}{\partial \,\theta}Q_{\pi}(s,a_0)$ ,这里的 $g(a_0,\theta)$ 我们称之为 $\frac{\partial \,V_{\pi}(s_t,\theta)}{\partial \,\theta}$ 的一个无偏估计。

3. 算法

这里我们还有第三步没有解决：对 $Q_{\pi}(s_t,a)$ 进行估计，我们知道 $Q_{\pi}(s_t,a)$ 是return的期望，所以我们可以用期望的计算公式 $u_t=\sum_{i=0}^{\infty}\gamma^ir_{t+i}$ 来近似 $Q_{\pi}(s_t,a)$ 或者再用一个神经网络来拟合 $Q_{\pi}(s_t,a)$