1 能量分析技术
1.1 能量分析概述
密码设备在进行加解密运算时,其内部结点电平高低变换完成运算,电平变换过程中电容不断地充放电进而从电源源源不断的获取电流。由于内部电阻的存在,此时设备不断地产生能量,并散发出去。同时,由于执行操作及被操作数的不同,电路从电源获取的电流是动态变化的,变化的电流产生变化的磁场。侧信道能量分析使用了密码设备能量消耗与执行操作及被操作数直接的相关性进行密码分析。
运算(电平高低变换)->电容充放电(产生电流)->存在电阻(产生能量)->电流是动态变化的(产生磁场)
- 能量分析是基于分析加密芯片加解密时电压、电流信息,转换为能量信息进行分析。
- 电磁分析与能量分析的数据对象不同,在信号的处理方法上略有不同,但在采集方法与分析技术上与能量分析非常类似。
能量分析也称为功耗分析,主要通过分析密码设备运行时的泄露能量信息,来分析得到密钥或与密钥有关的操作数据。
密码设备运行时的功率可以通过电压和电流计算得到。示波器是种高精度测量工具,只能测量电压信号,我们可以用示波器测量串联电阻的电压。由于电源电压不变,串联电阻上的电压降正比于密码设备的能量消耗。在密码设备的电源线上串联电阻是测量电路功耗的最简单的办法。
1.2 能量分析技术的发展与分类
自Kocher在1999年提出能量分析理论以来,这种分析方法已经历二十年的研宄,按照对侧信息的分析方法分类,将能量分析进一步分为简单能量分析SPA、差分能量分析DPA、相关性能量分析和模板分析等。
2 简单能量分析(SPA, Simple Power Analysis)
在SPA攻击方法中,攻击者直接分析密码运算过程中采集到的能量消耗。通过测定的能量轨迹直接推断出密码设备所执行的操作或所操作的数据。简单能量分析SPA方法使用了能量迹与设备所执行指令之间的依赖关系。
下图是整个DES操作过程中的能耗跟踪轨迹,可以很明显的观察到DES的16轮操作: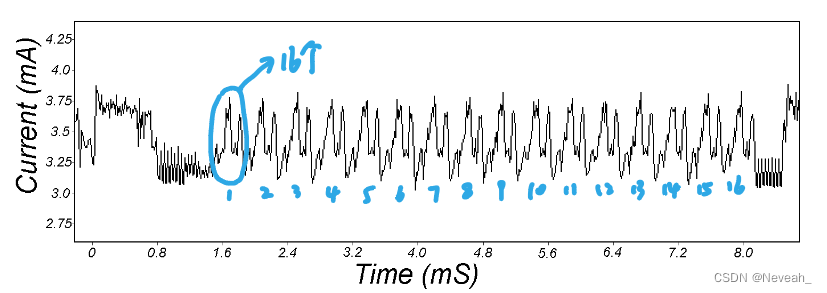
芯片中一些大的工作特点,如DES的每一轮操作以及RSA的模乘-平方等操作变化很明显。智能卡处理这些操作时会在一些时段出现较大的区别,这些都可以通过直接观察功耗波形来进行区别。SPA方法简单,但因为是直接观察系统的功耗,需要对电路的工作原理有很深的了解。在高精度的测量下,智能卡中执行的指令的差异可以被观测出来,例如RSA算法中乘法运算与平方运算之间的差异;DES算法中置换和移位操作之间的差异。SPA通过这些区别来攻击加密算法,被证实有一定的可行性。
SPA通过平均的措施将外部噪声消除,但没有消除算法噪声,只能用于分析智能卡等结构简单的电路。如果算法实现中存在数据依赖分支,即分支条件与数据有关,则SPA将非常有效。如RSA存在分支条件,SPA对其攻击就非常有效。
3 差分能量分析(DPA, Differential Power Analysis)
DPA是一种高效低成本的攻击方法,不需要知道被攻击芯片的具体内容。该技术利用加密运算的特点和统计分析技术来推测加密系统中的关键信息,即利用它们获取保存在智能卡内部的数据,而且搜索的密钥空间大大小于目前已知的几种密码分析方法,只需要大约1000次加密,几乎可以破解所有的智能卡。他们的研究表明,没有任何防御措施的智能卡将容易受到攻击。
DPA利用不同数据对应的条件功耗分布的差异推断数据,它是一种统计分析方法,统计分析方法的抗噪声能力强于SPA,而且更加难以预防,应用更为广泛。SPA攻击主要利用可见的重复采样和对芯片技术的了解来识别相关的功耗波动,而DPA攻击则使用统计分析和误差修正技术来提取与密钥相关的信息。那些SPA可能感觉不到的信息通常可以用DPA方法提取出来。一个完全不懂得智能卡技术的编程人员完全可以利用专用程序对没有DPA防范的智能卡芯片实现攻击。除了指令的执行顺序会影响功耗外,指令执行时所处理的数据也会影响功耗,这种影响虽小,有时更会被噪声或错误的量测所覆盖消耗,但依靠统计的方式还是可以看出端倪。DPA是一种以功耗曲线图为基础,再以统计方式推演主密钥的攻击技术。
4 对于DES的差分能量攻击
4.1 DES加密过程
下图是DES的算法流程,有16轮相同的结构: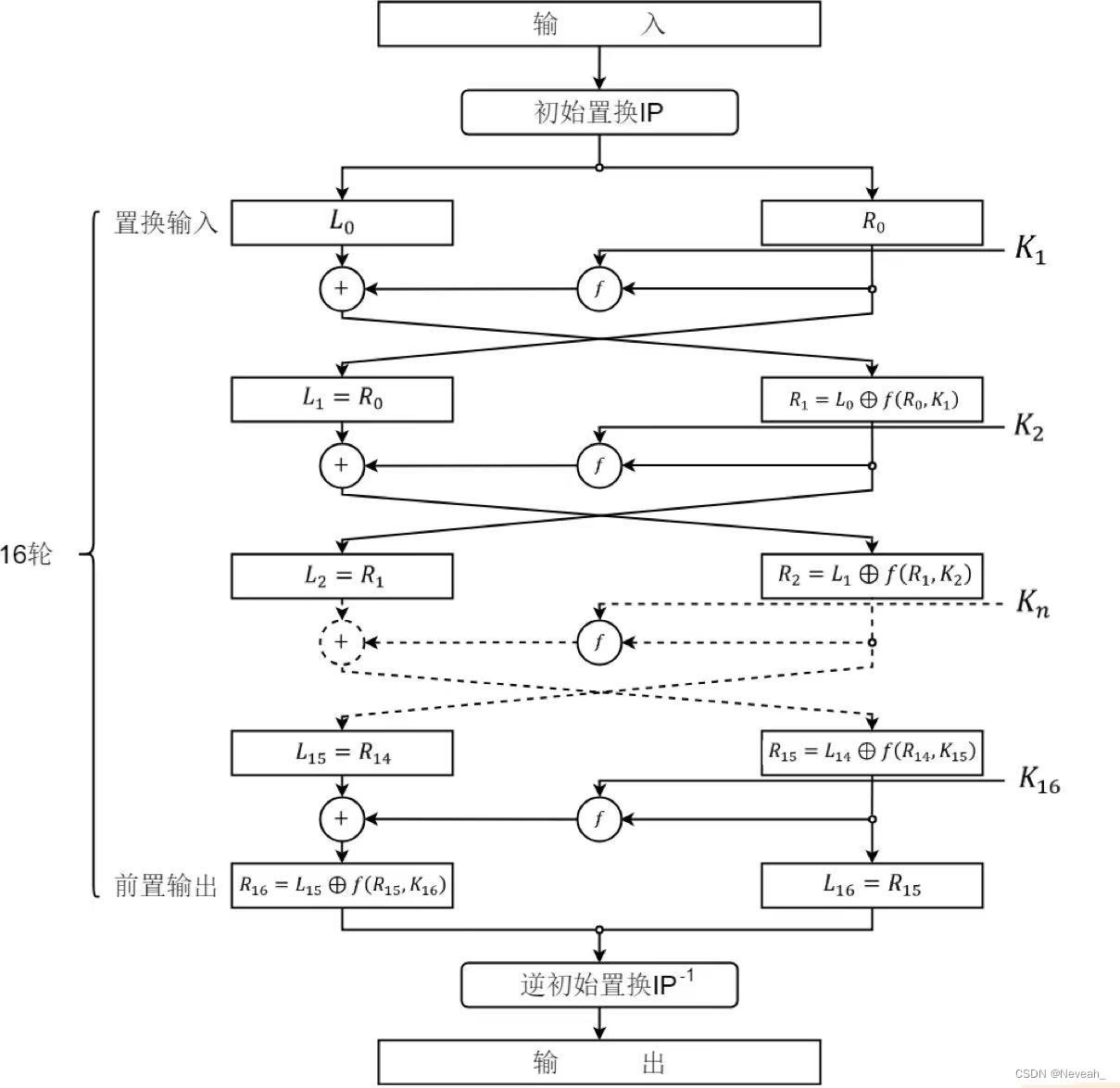
下图是其中一轮的结构。绿色框里是F函数的结构: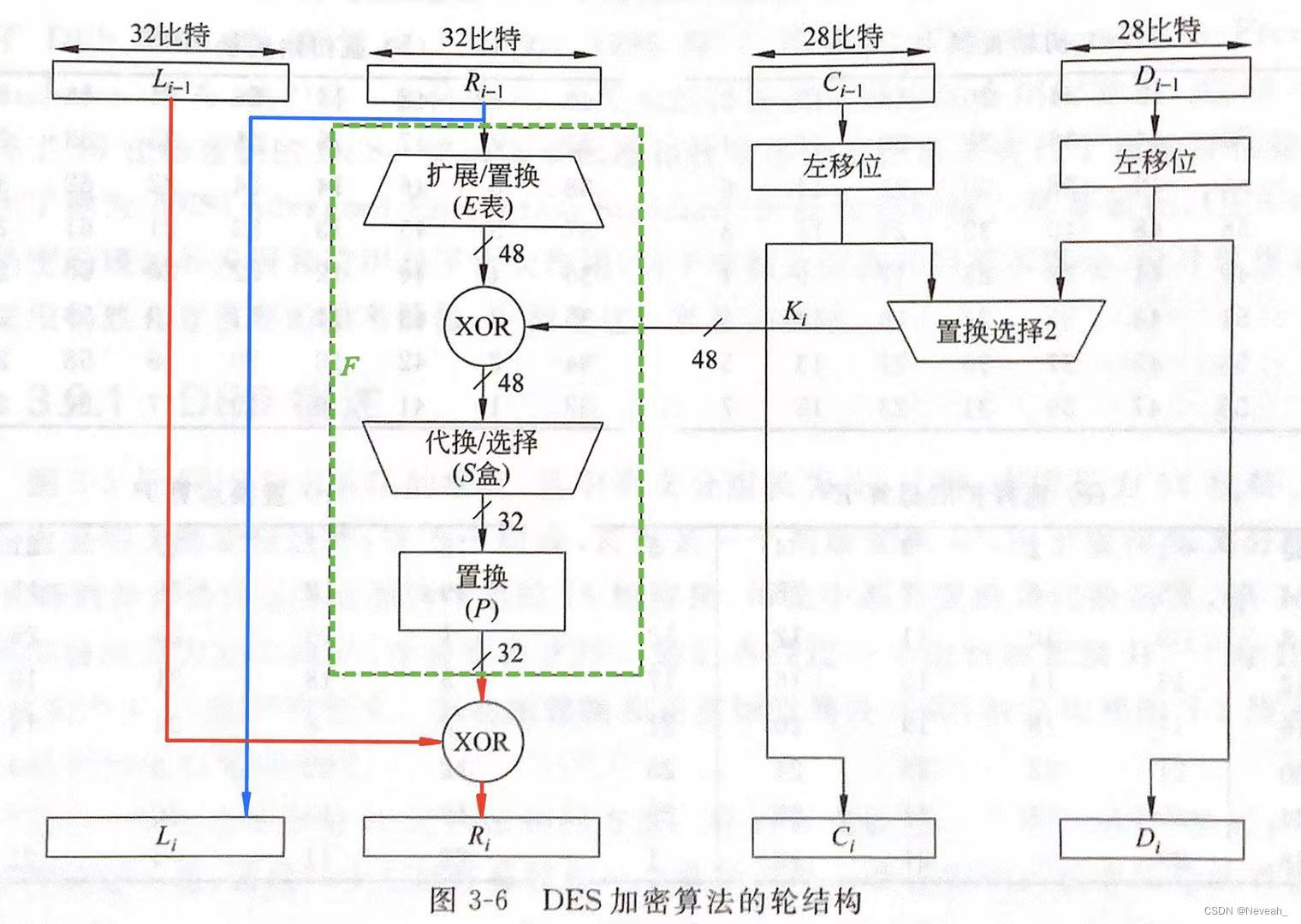
下图是对F函数更加细致的绘制。可以看到一个S盒的四位输出仅仅取决于轮秘钥当中的6位: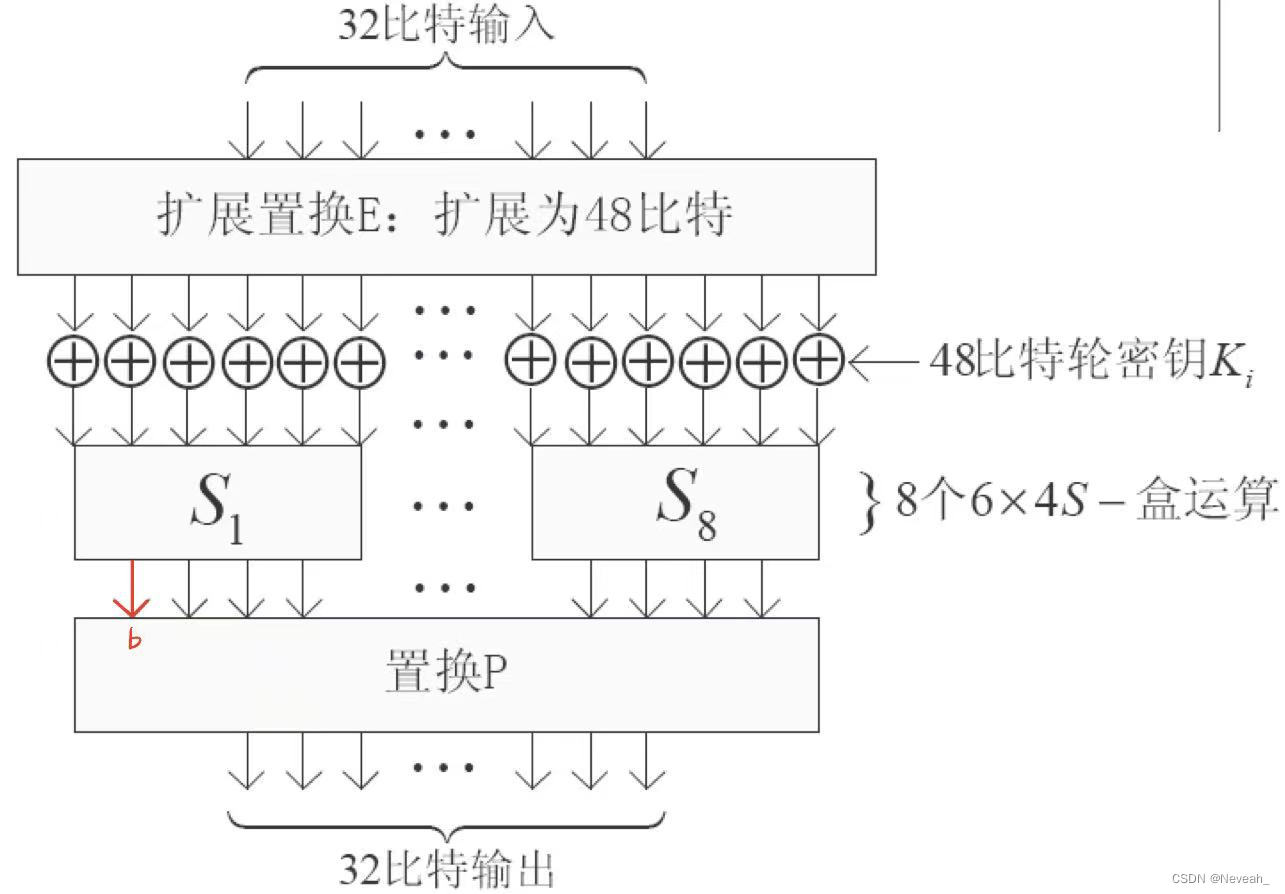
4.2 DPA攻击DES
DES密码算法及其使用的表格、函数皆为公开的数据,唯一不公开的数据仅剩主密钥。因此DES算法的安全依赖于主密钥的安全。对于攻击者来说,只要破解
K
i
K_i
Ki ,就可以倒推出主密钥的48位,剩下的8位奇偶校验码可用穷举法获得。DPA技术就是先破解DES的子秘钥
K
i
K_i
Ki进而破解DES的主密钥。
在对DES算法DPA攻击时,一般有两种策略:
- 攻击参与DES的第一轮运算的48位子秘钥;
- 攻击参与DES的最后一轮运算的48位子秘钥;
无论猜出那一轮的48位子秘钥,均可根据子秘钥运算原理,再结合对另8位秘钥的穷举,逆推出原始的56位秘钥。
在具体讨论这种攻击之前,对所用的符号做如下约定:
S i [ j ] S_i[j] Si[j]:第 i i i个明文在时间点 j j j时的能量消耗抽样值;D ( ∗ ) D(*) D(∗):分区函数;S 0 = { S i [ j ] ∣ D ( ∗ ) = 0 } S_0=\begin{Bmatrix} S_i[j] | D(*)=0 \end{Bmatrix} S0={Si[j]∣D(∗)=0}; (1)S 1 = { S i [ j ] ∣ D ( ∗ ) = 1 } S_1=\begin{Bmatrix} S_i[j] | D(*)=1 \end{Bmatrix} S1={Si[j]∣D(∗)=1}; (2)A 0 [ j ] A_0[j] A0[j]:集合 S 0 S_0 S0中所有信号在 j j j时刻的平均能量消耗;A 1 [ j ] A_1[j] A1[j]:集合 S 1 S_1 S1中所有信号在 j j j时刻的平均能量消耗;Δ D [ j ] \Delta_{D[j]} ΔD[j]:两集合的平均信号能量差异。
这里以攻击DES的第一轮为例:
step1:首先测得整个加密流程中S盒第一轮的能量消耗曲线。基于统计学的理论要求记录足够的样本点,例如分别测出1000个不同的明文下的S盒能量消耗
S
1
[
j
]
S_1[j]
S1[j],…,
S
i
[
j
]
S_i[j]
Si[j],…,
S
1000
[
j
]
S_{1000}[j]
S1000[j]。
step2:然后关注第一个S盒在第一轮运算中的4bits输出中的第一个bit,用
b
b
b表示。很容易发现
b
b
b仅仅取决于最后一轮秘钥当中的6bits。
step3:根据
b
=
0
b=0
b=0和
b
=
1
b=1
b=1将能量消耗曲线分为两类
S
0
S_0
S0和
S
1
S_1
S1。
从上面的(1)式和(2)式可以看出,分区函数
D
(
∗
)
D(*)
D(∗)的作用是将样本曲线映射到两个不相交的集合上。这里我们还没有给出具体的分区函数,这是因为,分区函数的设置并不唯一,有多种方法,但是分区函数的选取一般要满足一定的规则。这里,我们按照比特
b
b
b的取值设置分区函数(后面会给出具体的分区函数),这样一来,能量消耗曲线就可以反映出密钥的信息。这是整个DPA过程中的关键。
step4:下一步,分别计算这两类能量消耗曲线的平均值,即分别对集合
S
0
S_0
S0和
S
1
S_1
S1中的样本在时间
j
j
j的样本值进行平均,得到时间点
j
j
j时的平均能量消耗。
由于
S
i
[
j
]
S_i[j]
Si[j]包含
信号
和
噪声
这两部分的能量消耗,而根据随机过程的知识,知道其中大部分均值为0。因而这种平均可以在一定程度上降低随机噪声对信号的影响。
step5:再用(4)式可求得平均信号能量差异:
step6:随着样本点
i
i
i的增加,(4)式可用下面的表达式近似:

由上面可以看到:当
∣ Δ D [ j ] ∣ |\Delta_{D[j]}| ∣ΔD[j]∣ 较大时,说明由区分函数划分的两个信号的能量消耗在 j j j时刻差异较大。而这种能量消耗差异,正是由密钥和待处理数据相互作用而产生的。如果选择的区分函数合适,即在理想的情况下,
D D D函数可以正好将所有在 j j j时刻芯片处理数据为1的 S i [ j ] S_i[j] Si[j]选到集合 S 1 S_1 S1;相应地,在 j j j时刻,芯片处理的数据为0的所有 S i [ j ] S_i[j] Si[j]被 D D D函数映射到集合 S 0 S_0 S0中,这时能量消耗差异很明显。分区函数的具体定义为:
D ( P 6 , K 1 ) = { S b o x 1 ( P 6 ⊕ K 1 ) } 0 (6) D(P_6, K_1)=\begin{Bmatrix} Sbox1(P_6\oplus K_1)\end{Bmatrix}_0 \tag{6} D(P6,K1)={Sbox1(P6⊕K1)}0(6) 其中, P 6 P_6 P6表示明文经过初始置换后作为第一个S盒输入的6bits; K 1 K_1 K1表示猜测的第一轮密钥中用于第一个S盒的输入部分,也是6bits;分区函数的定义还有很多其他的例子。
step7:观察(6)式发现,D值等于第
i
i
i个样本在第一轮非线性变换中的第一个S盒输出的4bit中的第一个比特。
- 如果猜测的密钥 K 1 K_1 K1正确,那么 D D D值就一定会等于实际加密过程中第一个S盒的第一位输出。即这一时刻所有输出为1的 S i [ j ] S_i[j] Si[j]都会被映射到集合 S 1 S_1 S1,因此会使得 Δ D [ j ] \Delta_{D[j]} ΔD[j]出现峰值。这时因为同一电路在运行不同的数据时具有不同的功耗,因此当 b b b值为1时的电路功耗和 b b b值为0时的功耗将存在差异。
- 相反,如果密钥不正确,就会使得某些输出值为1的 S i [ j ] S_i[j] Si[j]映射到集合 S 0 S_0 S0,这时 Δ D [ j ] \Delta_{D[j]} ΔD[j]的峰值会变小。
step8:这样,对6位的
K
1
K_1
K1进行穷举,即猜测
2
6
2^6
26次,让
Δ
D
[
j
]
\Delta_{D[j]}
ΔD[j]出现峰值的即为正确的密钥。密钥一共48位,一共有8个S盒,所以要猜测
2
6
×
8
2^6\times8
26×8次。另外8比特密钥可以用穷举法求得。这个结果比单纯地应用穷举搜索有了明显的改进。
至此,就实现了对DES的差分能量攻击。
DPA关键点在于消除了算法级噪声,SPA则没有消除。DPA之所以可以仅仅定位一位数据,是因为,当输入的明文数据是随机的时,
b b b位以外其位的变化和 b b b位都是独立的。与 b b b不相关的部分都可以认为是近似随机变化,根据统计学规律,他们大量归类后特征相互抵消,统计后几乎没有差别。
参考文献:
对于DES的差分能量分析攻击及其防范对策
基于侧信道分析的密码算法安全评估技术研究
加密芯片的旁道攻击防御对策研究
版权归原作者 紫薯悦饼 所有, 如有侵权,请联系我们删除。