写在最前面:
上篇文章说了在GeoDa里面去自定义空间权重关系,有的同学问,在ArcGIS里面怎么做呢?我做过一个小视频,需要的同学在虾神的公众号里面发送“空间权重矩阵”六个字,就可以获得了。
前面的文章说到,在分析的数据里面,分布是这个样子的:
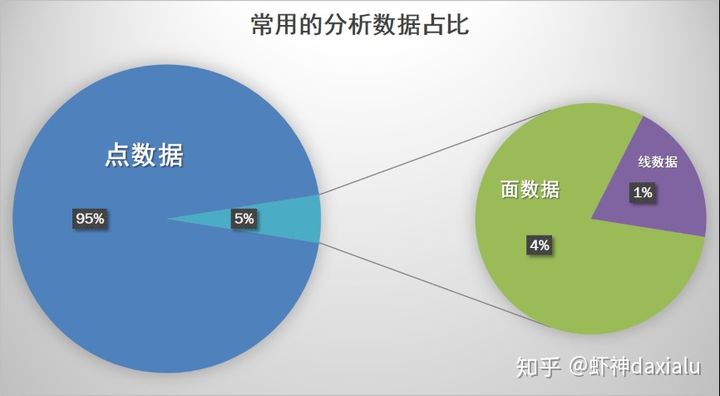
在所有数据里面,点数据是最容易获取到的,都不需要专业的软件,一个文本就可以制作,而点数据的获取,只要能上网就能从各种互联网地图上获取到,比如X度地图坐标拾取系统:
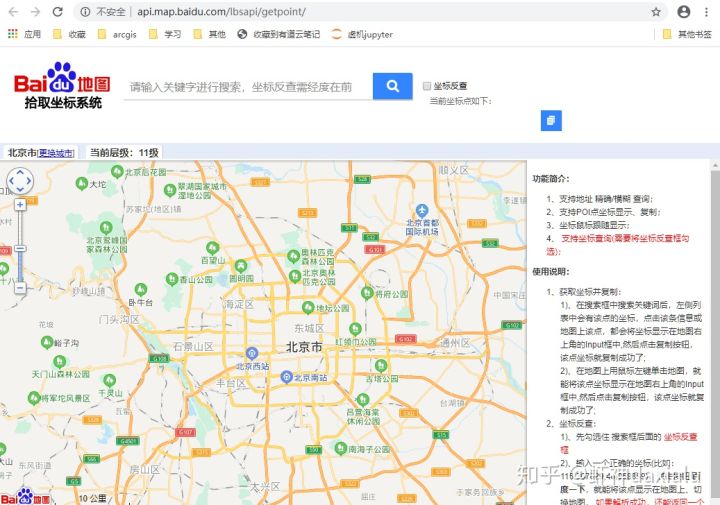
而只要有坐标,就可以轻而易举的变成空间数据,比如下面这份我用了无数次的北京市三级及以上的医院数据:
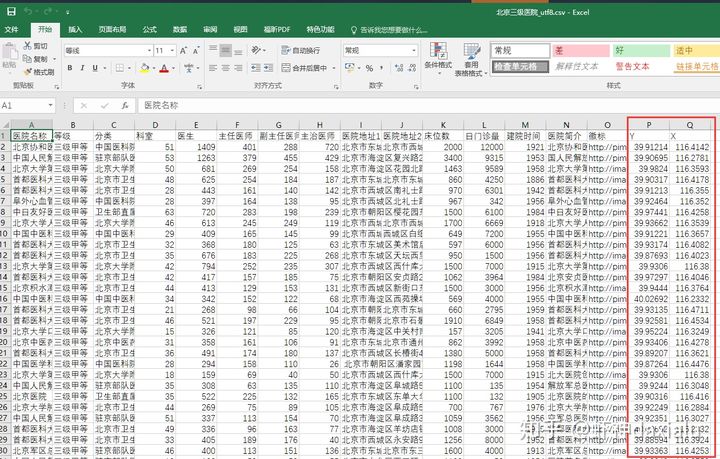
只需要后面有个经纬度,就可以变成空间数据了,这要比获得一个面状数据容易无数倍。
当然,有同学要问我,怎么去获取这些数据,请自行学习Python的天赋技能爬虫,不过——

关于爬虫相关的法律科普,见虾神以前的一篇文章:
爬虫与美国机场分布数据(知乎贴不出来,大家在微信公众号里面找)
下面我们继续来说点数据的临近关系。
点是一个逻辑概念,没有大小高矮宽窄边界方向长度这种物理概念,点仅能表示一个位置,可以无穷大,也可以无穷小,所以两个点之间,就有且只有两种关系:
分离:

重合:

所以,我们在做点临近关系的时候,通常用的是以下两种:

但是,如果两个点重合,在计算的时候就会带来新的问题,重合点的属性不一致的时候,到底是那个点代表当前位置?
所以在数学表达的时候,重合点这种情况,很容易会被表现成正无穷大,这样计算的时候就很尬尴了。
在ArcGIS里面,建议做点数据分析的时候,先调用一个工具,叫做“收集事件”,就是用来处理重合点的:
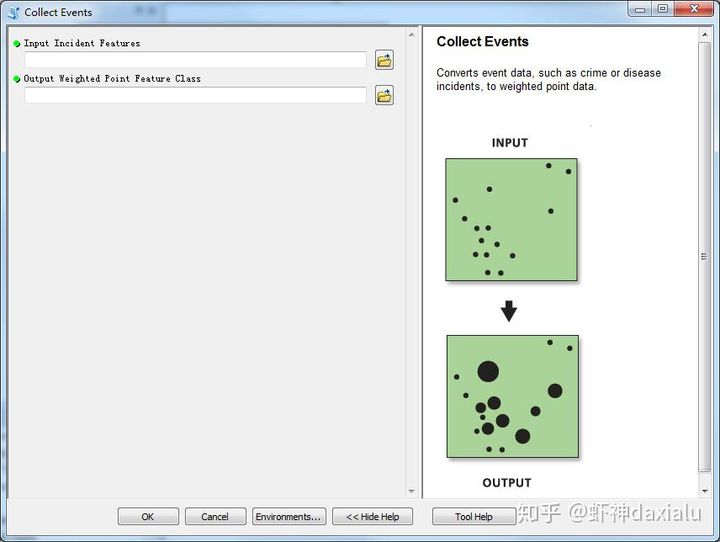
因为反距离模式,在前面我们已经讲过了,这里就不赘述了,大家可以回去看第十五节:
现在我们来讲讲几种在点要素上适用的空间关系:
第一种,就是K临近:
所谓的K临近,就是指在一定的数目范围内,都算相邻的要素,这个概念是“距离范围”模型改良之后生成的。距离范围是以一定距离为阈值,而这个模型是以要素的个数为阈值的。
比如,你选定了K=8,那么这个要素周边的8个要素,都将作为你的相邻要素参与计算,这是一种搜索距离可变的模型,如下:
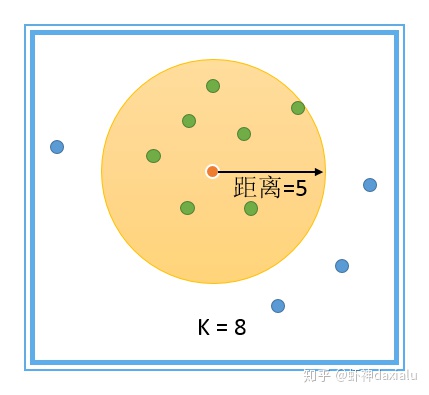
在中心点附近,选择你最近的k个点,组成你的邻近要素集,这个距离是可变的,如果要素分布的比较离散,那么搜索的距离就会变大,如下:
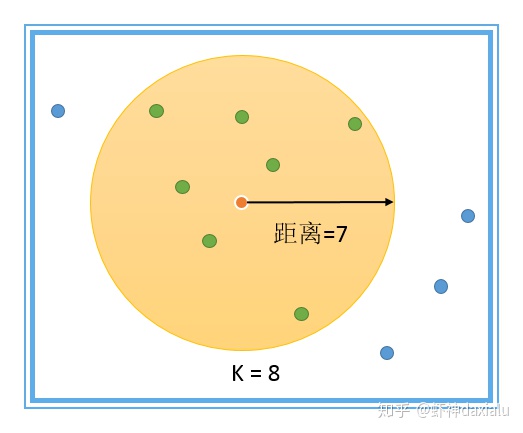
这种模型的优点,在于它可以确保每个目标要素都能找到相邻的要素,特别是在一些在研究区域内,要素分布非常不均匀的,密度差别非常大的情况下,也能保证有相邻要素的存在。
K邻近模型在一些数学研究中有很广泛的应用,例如在素数的研究中,因为素数是随机在数轴上出现的,所以你无法圈定的一个固定的范围,来决定你的相邻要素(素数有孪生素数问题,也就是相邻可能只有1:比如3和5,5和7,17和19这种,当然,两个素数之间距离也可能无穷大),所以如果要获取一些邻近要素的时候,就只能去选择这一类的模型了。
因为我们通常无法非常好的去确定,你到底需要几个临近要素,所以k临近的K值不太好确定,这样就产生了另外一种临近模型:自然临近。
自然临近模型,有时候也叫做Delaunay 三角测量临近模型。其算法是俄罗斯著名数学家鲍里斯 尼古拉耶维奇 德劳内(Boris Nikolaevich Delaunay 1890-1980)在1934年最先提出来的,用于对点集进行三角网划分的方法。

罗斯(前苏联)传奇数学家
鲍里斯 尼古拉耶维奇 德劳内(Boris Nikolaevich Delaunay )
1890-1980
ps:毛熊家的数学家们把工程数学玩到了极值,先不说苏式战机那漂亮的倾城倾国的气动外形:

图160战略轰炸机
俄罗斯代号:白天鹅
北约代号:海盗旗

苏式战机的颜值巅峰:su27战斗机
我国引入,全国产化之后,命名为J11。
话说当年国内仿造某型号米格战斗机,发动机上的一个齿轮,因为我国加工工艺不过关,所以角度稍微多了一点几度,本来以为这点点角度不是问题,可是飞机一上天之后,就是这不到2度的误差,导致齿轮应力急剧增加,然后咔嚓一下四分五裂,导致机毁人亡——

真的——我就只多了这么一点点
可以看出毛熊数学家们在工程数学上,真是玩到了极值,一点容错都不给,所以在材料、科技都不如美帝的情况下,生生用数学撑起了苏式武器的一片天空。
言归正传:
既然叫做自然相邻,那么它就不需要人为的定义任何一个约束条件和参数,直接利用要素的空间位置来决定谁是它的相邻点。核心原理是:将点作为若干三角形的顶点,如果两个点共同属于同一个三角形,则认为两个点是相邻点,如下所示:

点E,与A\B\D三个点,是自然相邻要素。
而在空间关系概念化模型里面,利用这个方法来确定相邻要素,其算法是一种很有意思的方法。具体的做法,是首先利用点(如果是面要素的话,就利用面的质心点)来创建一个 Voronoi 三角形,使得每个点(质心)都是三角形结点。
如下图:
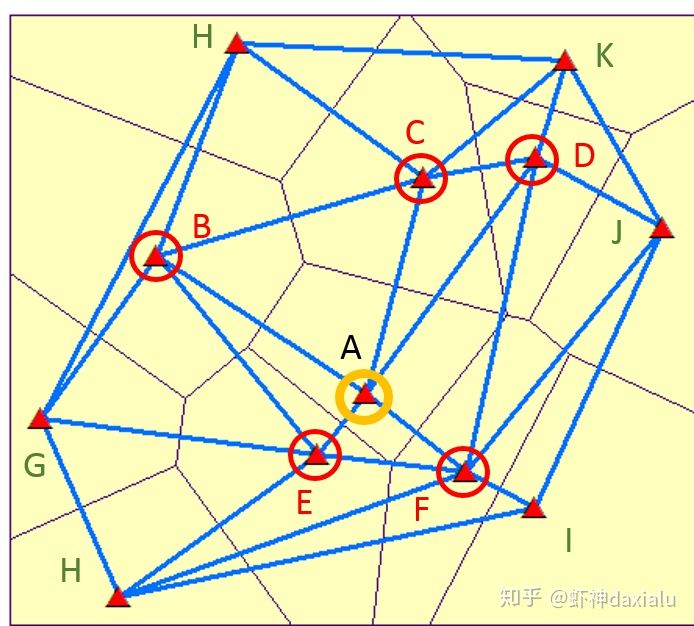
A点与B、C、D、E、F,都有共同的三角网,那么BCDEF五个点,就被设为A点的相邻要素。
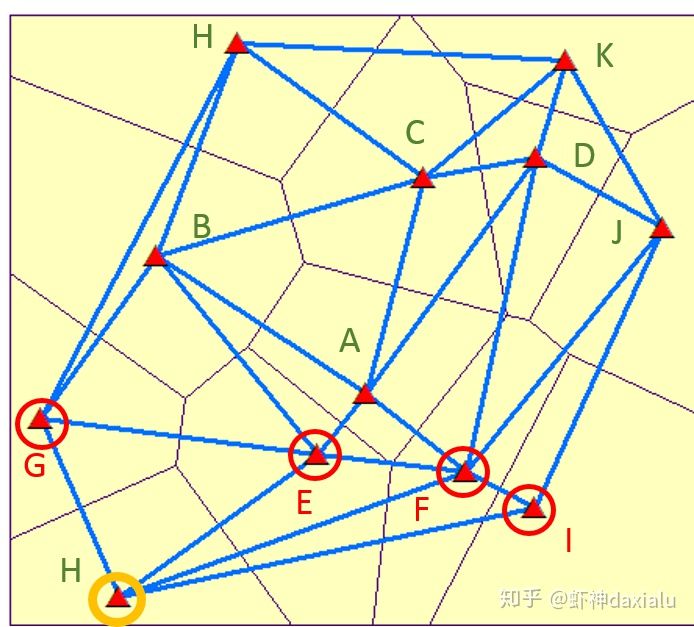
同样的如果要计算H点的相邻要素,就变成了E、F、I、G了,如下:
使用 Delaunay 三角测量模型,和K邻近一样,可以确保你要计算的每个要素至少具有一个相邻要素,即使你的数据包含有岛状要素或者带有空洞的要素。另外,这个模型和K邻近一样,不会在乎你的要素分布是不是均匀。
需要注意的是,如果你的数据出现了重合要素的时候,不要使用 Delaunay 三角测量选项。
点数据分析,最忌有重合!
点数据分析,最忌有重合!!
点数据分析,最忌有重合!!!
重要是事情说三遍。
本节打完收工,待续。
版权归原作者 虾神说D 所有, 如有侵权,请联系我们删除。