过了一天,我本来觉得这个题很多人在写,我就不写了,但是应大家要求,我还是写一篇D题导读。
读题
开头部分都是些废话,直接看重点,它需要解决的问题是什么?就是让你布置一些站点,放在信号不好的地方
接着就是考虑一些其它因素,让你把成本,业务量考虑进来,业务量优先呗,成本肯定尽量低咯
接下来又说,把这一片区域基金分成了很多的格子,每个格子只考虑中心点,就像把你的学校划分为食堂,教学楼A,教学楼B…每一个中心点都有它现在的坐标,是不是信号弱,业务量如何,就像食堂A在坐标(110,20),这里的5G信号贼好,就几乎不需要再装新的基站。
继续读题,意思就是每个基站的覆盖范围,从平面来看就是一个正圆呗。
图丑了,重新画一下:p点能覆盖这么一整个圆形的面积,使得这一部分信号为信号不弱。
最后一句话就是说不要让基站太近了,这么近得建立多少啊,血亏钱钱了。
第一题
题目就是给你了一个正方形的区域,然后单元格形式有对应那么多的点。宏基站的覆盖范围是30,也就是半径30嘛,成本10,咱也不管啥单位,它现在也没给。微基站半径就是10,成本还挺低,才1。附件一给了信号不好的区域:
继续读,它说有附件二,给出了目前已经有的基站位置坐标,要求各个基站距离不能低于10.
大概就是这样的形式…猜一下呗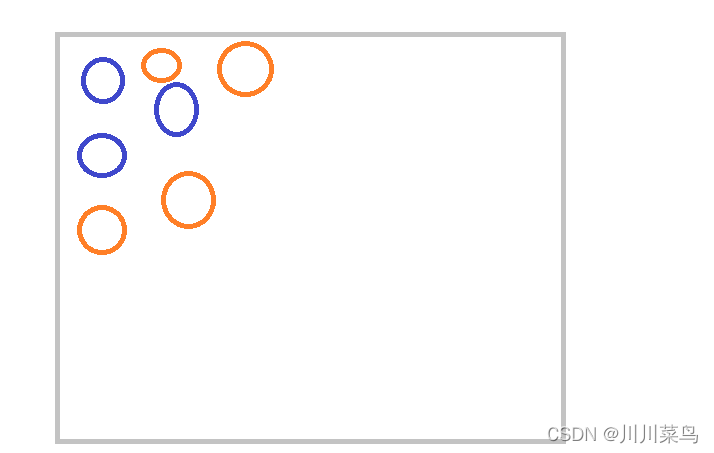
看一下要求,划重点了:
先来看附件一,这些坐标都是信号不好的地方:

附件二呢?信号好的地方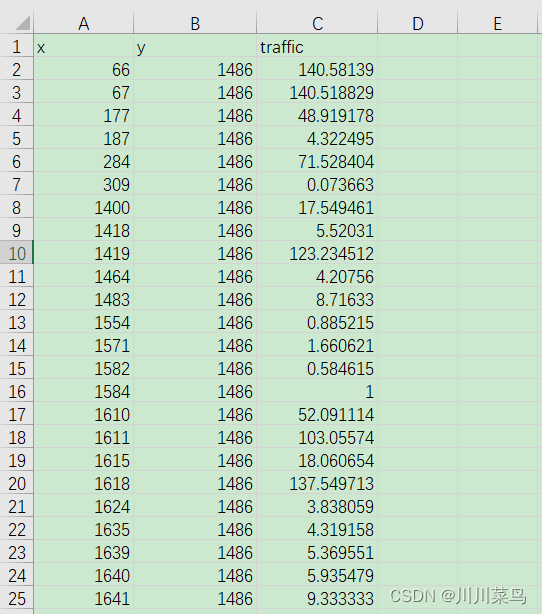
从严谨的角度来说,你应该把两个数据表合并到一块,才能计算新建立的站点与已经有的站点距离。先说一下怎么算新建立站点?可能真的要把这些点进行聚类…
聚类算法有哪些?别一堆人去扎kmeans,还有你知道什么是kmeans吗?为此我专门写了一篇kmeans和knn区别,链接:https://zhuanlan.zhihu.com/p/498648916
聚类算法有如下几种:
- K-Means(K 均值)聚类,K-Means 的优势在于速度快,因为我们真正在做的是计算点和组中心之间的距离:非常少的计算!因此它具有线性复杂度 O(n)。K-Means 有一些缺点。首先,你必须选择有多少组/类。这并不总是仔细的,并且理想情况下,我们希望聚类算法能够帮我们解决分多少类的问题,因为它的目的是从数据中获得一些见解。K-means 也从随机选择的聚类中心开始,所以它可能在不同的算法中产生不同的聚类结果。因此,结果可能不可重复并缺乏一致性。其他聚类方法更加一致。K-Medians 是与 K-Means 有关的另一个聚类算法,除了不是用均值而是用组的中值向量来重新计算组中心。这种方法对异常值不敏感(因为使用中值),但对于较大的数据集要慢得多,因为在计算中值向量时,每次迭代都需要进行排序。
- 均值漂移聚类。与 K-means 聚类相比,这种方法不需要选择簇数量,因为均值漂移自动发现这一点。这是一个巨大的优势。聚类中心朝最大点密度聚集的事实也是非常令人满意的,因为理解和适应自然数据驱动的意义是非常直观的。
- 基于密度的聚类方法(DBSCAN)。DBSCAN 是一种基于密度的聚类算法,它类似于均值漂移,DBSCAN 与其他聚类算法相比有很多优点,首先,它根本不需要固定数量的簇。它也会将异常值识别为噪声,而不像均值漂移,即使数据点非常不同,也会简单地将它们分入簇中。另外,它能够很好地找到任意大小和任意形状的簇。
- 高斯混合模型(GMM)的最大期望(EM)聚类,K-Means 的一个主要缺点是它对于聚类中心均值的简单使用,K-Means 在簇不是圆形的情况下处理会失败。高斯混合模型(GMMs)比 K-Means 给了我们更多的灵活性。对于 GMMs,我们假设数据点是高斯分布的;相对于使用均值来假设它们是圆形的,这是一个限制较少的假设。这样,我们有两个参数来描述簇的形状:均值和标准差!以二维为例,这意味着,这些簇可以采取任何类型的椭圆形(因为我们在 x 和 y 方向都有标准差)。因此,每个高斯分布被分配给单个簇。
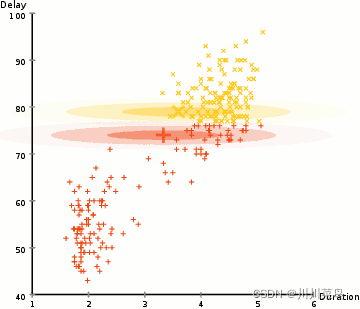
- 使用 GMMs 的 EM 聚类。使用 GMMs 有两个关键的优势。首先,GMMs 比 K-Means 在簇协方差方面更灵活;因为标准差参数,簇可以呈现任何椭圆形状,而不是被限制为圆形。K-Means 实际上是 GMM 的一个特殊情况,这种情况下每个簇的协方差在所有维度都接近 0。第二,因为 GMMs 使用概率,所以每个数据点可以有很多簇。
- 凝聚层次聚类。层次聚类不需要我们指定簇的数量,我们甚至可以选择哪个数量的簇看起来最好,因为我们正在构建一棵树。层次聚类方法的一个特别好的例子是当基础数据具有层次结构,并且你想要恢复层次时;其他聚类算法不能做到这一点。与 K-Means 和 GMM 的线性复杂度不同,层次聚类的这些优点是以较低的效率为代价的,因为它具有 O(n³) 的时间复杂度。
参考:
https://towardsdatascience.com/the-5-clustering-algorithms-data-scientists-need-to-know-a36d136ef68
问题二
该问题说到,信号会发生减弱问题,把一个圆形划分为三个扇形,一个扇形120度,从中间往两边30度都能覆盖,超过30度就开始减小:
画个图说明一下,以其中一个扇形为例:,红色区域是完全覆盖,超过这个红色区域就开始减弱: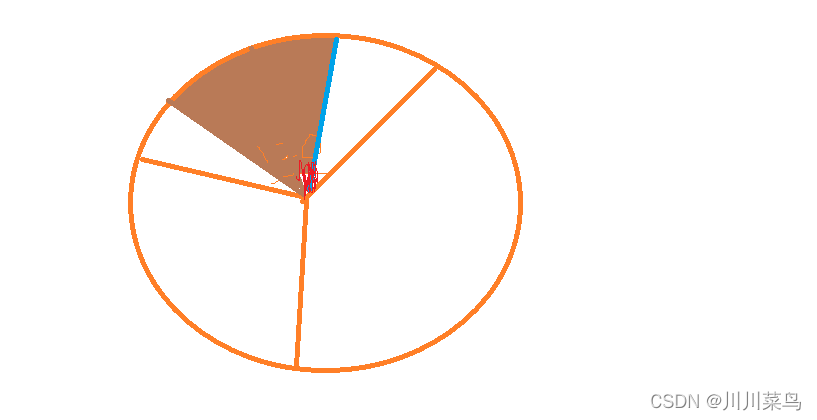
后面就是一些要求寻优,有点像规划类
以上内容仅仅是个人阅读所想,不代表是正确。
版权归原作者 川川菜鸟 所有, 如有侵权,请联系我们删除。