算法leetcode｜81. 搜索旋转排序数组 II（rust重拳出击）

文章目录

81. 搜索旋转排序数组 II：

已知存在一个按非降序排列的整数数组

nums

，数组中的值不必互不相同。

在传递给函数之前，

nums

在预先未知的某个下标

k

（

0 <= k < nums.length

）上进行了 旋转 ，使数组变为

[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]

（下标 从 0 开始 计数）。例如，

[0,1,2,4,4,4,5,6,6,7]

在下标

5

处经旋转后可能变为

[4,5,6,6,7,0,1,2,4,4]

。

给你 旋转后 的数组

nums

和一个整数

target

，请你编写一个函数来判断给定的目标值是否存在于数组中。如果

nums

中存在这个目标值

target

，则返回

true

，否则返回

false

。

你必须尽可能减少整个操作步骤。

样例 1：

输入：
    
    nums = [2,5,6,0,0,1,2], target = 0
    
输出：
    
    true

样例 2：

输入：
    
    nums = [2,5,6,0,0,1,2], target = 3
    
输出：
    
    false

提示：

• 1 <= nums.length <= 5000
• -104 <= nums[i] <= 104
• 题目数据保证 nums 在预先未知的某个下标上进行了旋转
• -104 <= target <= 104

进阶：

• 这是 搜索旋转排序数组 的延伸题目，本题中的 nums 可能包含重复元素。
• 这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

分析：

• 面对这道算法题目，二当家的再次陷入了沉思。
• 如果没有旋转，那肯定使用二分查找，二分查找可以在每一次循环遍历都排除一半的数据，效率非常高。
• 要使用二分查找，数组必须是有序的，但是数组已经被旋转了，所以并不是完全有序，但也并不是完全没有办法。
• 一般的二分是每次比较中间元素，然后判断元素是否相等，如果不相等再看元素应该在左半部分，还是右半部分，由此排除一半的元素，再继续在另一部分中重复这样的逻辑。
• 我们可以使用变形的二分查找，可以想到，有序数组旋转后，从中分成两部分，一定有一部分是有序的，而另一部分也是部分有序，但是头一定不小于尾，所以我们可以先判断哪一部分有序，然后再看目标数字是否在有序那部分当中，来决定改变左边界，还是右边界，这样便可以达到二分查找的效率。
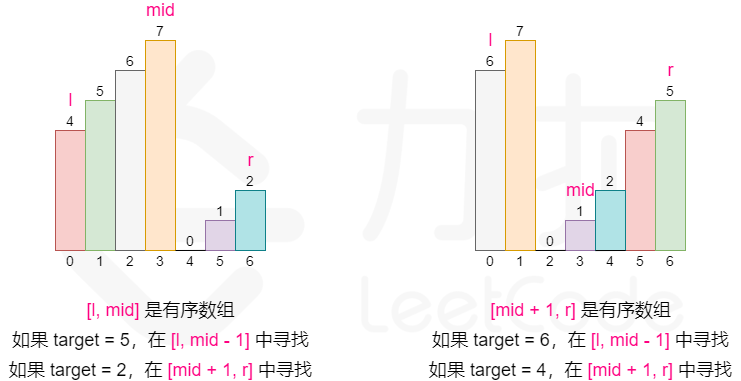
• 由于数组中允许重复元素，那么在某一次查找时，可能会出现中间元素和头尾元素都是相同的情况，这时候就没办法判断哪半部分是有序的，也就不能直接排除一半的元素，但是我们可以将头和尾的元素排除掉。

题解：

rust：

implSolution{pubfnsearch(nums:Vec<i32>, target:i32)->bool{let n = nums.len();if n ==0{returnfalse;}if n ==1{return nums[0]== target;}let(mut l,mut r)=(0, n -1);while l <= r {let mid =(l + r)>>1;if nums[mid]== target {returntrue;}if nums[l]== nums[mid]&& nums[mid]== nums[r]{if r ==0{// 防止r溢出到非常大returnfalse;}
                l +=1;
                r -=1;}elseif nums[l]<= nums[mid]{if nums[l]<= target && target < nums[mid]{
                    r = mid -1;}else{
                    l = mid +1;}}else{if nums[mid]< target && target <= nums[n -1]{
                    l = mid +1;}else{
                    r = mid -1;}}}returnfalse;}}

go：

funcsearch(nums []int, target int)bool{
    n :=len(nums)if n ==0{returnfalse}if n ==1{return nums[0]== target
    }
    l, r :=0, n-1for l <= r {
        mid :=(l + r)>>1if nums[mid]== target {returntrue}if nums[l]== nums[mid]&& nums[mid]== nums[r]{
            l++
            r--}elseif nums[l]<= nums[mid]{if nums[l]<= target && target < nums[mid]{
                r = mid -1}else{
                l = mid +1}}else{if nums[mid]< target && target <= nums[n-1]{
                l = mid +1}else{
                r = mid -1}}}returnfalse}

c++：

classSolution{public:boolsearch(vector<int>& nums,int target){constint n = nums.size();if(n ==0){returnfalse;}if(n ==1){return nums[0]== target;}int l =0, r = n -1;while(l <= r){int mid =(l + r)>>1;if(nums[mid]== target){returntrue;}if(nums[l]== nums[mid]&& nums[mid]== nums[r]){++l;--r;}elseif(nums[l]<= nums[mid]){if(nums[l]<= target && target < nums[mid]){
                    r = mid -1;}else{
                    l = mid +1;}}else{if(nums[mid]< target && target <= nums[n -1]){
                    l = mid +1;}else{
                    r = mid -1;}}}returnfalse;}};

python：

classSolution:defsearch(self, nums: List[int], target:int)->bool:ifnot nums:returnFalse

        n =len(nums)if n ==1:return nums[0]== target

        l, r =0, n -1while l <= r:
            mid =(l + r)>>1if nums[mid]== target:returnTrueif nums[l]== nums[mid]and nums[mid]== nums[r]:
                l +=1
                r -=1elif nums[l]<= nums[mid]:if nums[l]<= target < nums[mid]:
                    r = mid -1else:
                    l = mid +1else:if nums[mid]< target <= nums[n -1]:
                    l = mid +1else:
                    r = mid -1returnFalse

java：

classSolution{publicbooleansearch(int[] nums,int target){finalint n = nums.length;if(n ==0){returnfalse;}if(n ==1){return nums[0]== target;}int l =0, r = n -1;while(l <= r){int mid =(l + r)/2;if(nums[mid]== target){returntrue;}if(nums[l]== nums[mid]&& nums[mid]== nums[r]){++l;--r;}elseif(nums[l]<= nums[mid]){if(nums[l]<= target && target < nums[mid]){
                    r = mid -1;}else{
                    l = mid +1;}}else{if(nums[mid]< target && target <= nums[n -1]){
                    l = mid +1;}else{
                    r = mid -1;}}}returnfalse;}}

非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难，但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子：https://le-yi.blog.csdn.net/ 博客原创~