python代码实现Miller-Rabin算法及效率测试

python代码实现Miller-Rabin算法及效率测试

欢迎大家访问我的GitHub博客

https://lunan0320.github.io/

文章目录

一、算法描述

1、主要思路

把 n-1 写成 n-1=2k*m,其中 m 是一个奇数
随机选取整数 a，使得 1≤a≤n-1

2、伪代码描述

b=am mod n
if b≡1(mod n)
then return True
for i from 0 to k-1
if b≡n-1 *******注意此处写代码的时候需要改成n-1，算法描述的时候可以是-1mod(n)
then return True
else b=b2mod n

二、代码实现

1、Python代码实现过程如下：

import random
import time
defMillerRabin(n):if n in{2,3,5,7,11,13}:returnTrueelif n==1or n%2==0or n%3==0or n%5==0or n%7==0or n%11==0or n%13==0:returnFalse

    k=0#判断向右移动位数
    u=n-1#对u分解while u&1==0:
        k=k+1
        u=u>>1
    m=u
    a=random.randint(2,n-1)
    r=pow(a,m,n)if r==1:returnTrueelse:for j inrange(k):if r==n-1:returnTrueelse:
                r=pow(r,2,n)returnFalsedefgen_Random(length):
    n=random.randint(2**(length-1),2**length)return n

input_len=int(input("请输入比特长度(bit)："))sum=0
count=0whileTrue:
    count+=1
    n=gen_Random(input_len)
    begin=time.time()if MillerRabin(n):
        end=time.time()sum+=end-begin
        print(n,"是素数")print("随机生成素数总时间",sum,"s")print("平均素检测时间：",sum/count,"s")break
    end=time.time()sum+=end-begin

2、Miller-Rabin素性检测

3、获得给定长度的随机比特位串

4、测试效率部分

三、算法效率测试

实例1、

实例2、

实例3、

实例4、

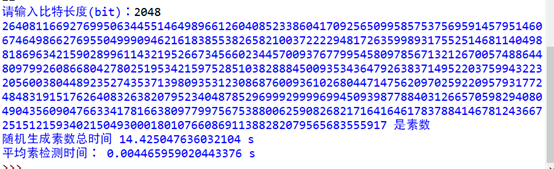
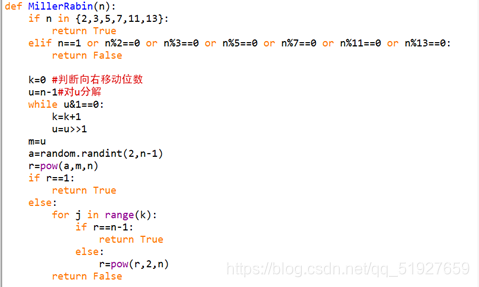
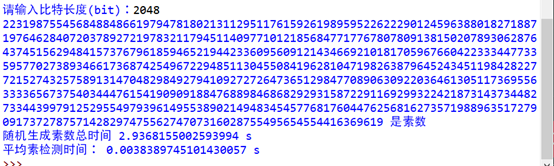
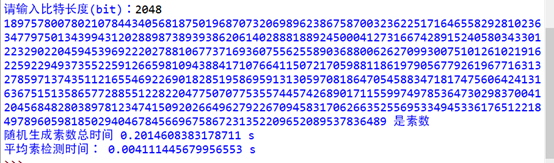
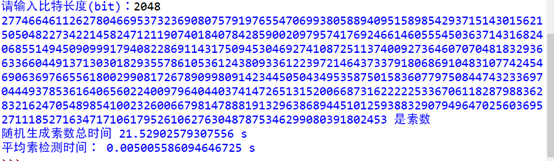
此处是随机生成一个2048bit的数字，判断其是否是素数，如果不是就继续生成，继续判断，知道生成一个素数时，去计算此过程平均素性检测时间（不包括生成一个2048bit串的时间）
可见，随机生成一个固定长度的素数的时间是不确定的，但是去判断这个数是否是素数的时间却基本维持在0.003~0.005左右
由此可得，Miller-Rabin算法是有较高的效率的

四、参考文献

[1] [加]Douglas R.Stinson《密码学原理与实践（第三版）》，电子工业 出版社，北京，2016