信息与网络安全 Diffie-Hellman密匙交换算法 题目练习

1.考虑公共素数q = 11本原元a = 2的Diffie-Hellman方案

（1）如果用户A有公钥YA = 9，请问A的私钥XA是什么？
（2）如果用户B有公钥YB = 3，请问共享的密钥K是什么？

解：

（1）根据Diffie-Hellman密钥交换原理——设g是一个质数，n是g的本原元，要求n和g是公开的，则网络中的某一用户可以任意挑选一个小于g的整数i作为秘密密匙。

    ①满足*a = n^i mod g (其中0 <= i <= (g-1))*

    ②代入*a = YA = 9 且 n = 2 且 g = 11 → 9 = 2^i mod 11*

    ③求得离散对数*i = XA = 6*

（2）由(1)可知，代入求得XB = 8。

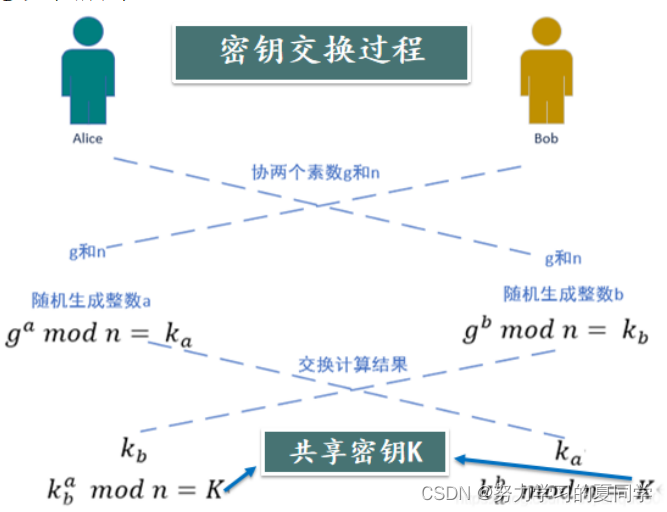
共享密匙K求解流程

①双方在基于本原元n和素数g，选择私有密匙XA和XB,得出各自的公开密匙YA,YB。

②(以A为例)使用自己的私有密匙XA和获取对方的公有密匙YB进行计算，得到共享密匙K。公式 YB^YA mod g = K

③如图所示

④代入YA = 9 且 XB = 8 得 9^8 mod 11 = K = 3

2.假设某人建议用如下方法来确认你们两个人是否拥有同一密钥：

①你创建了一个与密钥长度相等的随机比特串，将它和密钥进行异或，并通过通道发送结果。

②你的伙伴将得到的分组与密钥（应该和你的密钥相同）进行异或并发回它。

③你进行核对并且如果你接收到的是你的原始随机串，你就证实了你的伙伴拥有同一密钥，而且你们两个人都还没有传递过密钥。

这个方案有缺陷吗？

解：有缺陷

1. 不准确：双方密钥长度不确定相同，有可能对方的密钥的一部分和自己相同从而得到相同的异或结果。
2. 不安全：通道传输是透明的，因为只有异或解码难题，容易收到攻击被破解。
3. 易出错：因为为了确保解码足够安全，密钥长度往往很大，传递的比特串也同样很长，容易在传输过程中遗失或错误。

1. 假定网络中每一个节点N都被分派了一个独特的密钥Kn，这个密钥保证节点和服务器之间的安全通信。所有的密钥也被储存在服务器上。用户A希望发送秘密信息M给用户B,发起如下协议：

1.A生成一个随机数R并把自己的名字A，目标B和*E(Ka, R)*发送到服务器。

2.服务器把*E(Kb,R)*发送给A。

3.A把*E(R,M)和E(Kb,R)*发给B.

4.B知道Kb，所以解密*E(Kb,R)*获得R,随后使用R来解密M。

每个信息都被发送时都会生成一个随机数。当攻击者Z能截取保密节点之间的通信时，请分析攻击者Z如何利用该协议存在的安全问题而解密明文信息M?

(提示：攻击者Z会假装自己是A)

解：因为在协议运作过程中没有对于发送方的认证，因为KA默认只有用户A和服务器知道，但*E(KA,R)*在信道可能被攻击者Z截取，而伪装成A来获取明文M。流程如下

1. A向服务器发送信息*E(KA,R)*被截取
2. A(假)把自己的名字A,目标Z和*E(KA,R)*发送给服务器
3. 服务器返回E(Kz,R)
4. Z知道Kz,所以解密*E(Kz,R)*得到R,然后利用R来解密明文M。